Characteristics of Nanofluids over a Non-Linearly Stretched Sheet under the Influence of Thermal Radiation and Magnetic Field ()
1. Introduction
A nanofluid is a fluid which contains nanometer sized solid particles. Nanometer-size solid particles have unique chemical and physical properties. Since suspending nanometer-size particles to the conventional heat transfer fluids lead a better heat transfer, nanofluids are proposed to be employed in several applications such as transportation, nuclear reactors and electronics [1] .
Many engineering processing applications use the characteristics obtained by the flow studies over stretched surfaces includes extrusion, hot rolling, etc. For example, polymer sheets and filaments, in general use continuous extrusion of polymer form a die to the windup roller that is almost placed at a finite distance. The velocity in stretched surfaces almost differs from the plain surfaces and it will be proportional to the distance from orifice [2] . In a recent research conducted by various authors revealed that the mass and heat transfer in stretched and constant surfaces differs in various aspects [3] . Stretching problem on a permeable wall with incompressible fluid is studied by Magyari and Keller [4] . However, Vajravelu also studied the effect of flow and heat transfers in viscous fluids on a nonlinear stretched sheet under the absence of viscous dissipation [5] . All the above study cases are limited to linear stretching of sheets and nonlinear sheet stretching is not considered. However, the above authors highlighted exponential and nonlinear stretching. On the other side, a study on heat transfer characteristics of viscoelastic and viscous fluids on exponential stretched sheets are studied by various authors [6] [7] .
Apart from these, due to advancement of technology and introduction of nanotechnology the size of materials reduced to nanometres possesses special physical and chemical characteristics [8] . Chio used nano-fluids for the first time with a combination of nano-scaled particles along with fluids [8] . Further, these fluids are used on stretched materials and on vertical plates to experiment thermal conductivity and convective heat transfer properties [9] [10] [11] . In this paper, the study is being conducted to test the flow characteristics on a vertical plate and to study the nonlinearly stretching sheet with respect to viscous flow of nano fluids and heat transfer with magnetic field and thermal radiation.
To study these aspects, Keller-Box method is used and is known to be one of the best numerical methods included with mixed finite volume that considers the average of conservation laws and related constitutive laws [12] . Earlier the applications of this method were used by Hamad et al. [13] for the steady boundary layer similarity solutions for studying viscous flow and heat transfer characteristics on stretching sheets along with thermal radiation [13] . The importance of this paper is to understand the thermal radiation effect on stretched sheets along with various other factors discussed by previous researchers.
2. Mathematical Formulation
In this paper, the properties of viscous flow with respect to nano-fluid on a stretching sheets is considered. Generally the flow is possible when the condition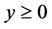 . Here, the term y is the normal coordinate with respect to the stretching sheet. Practically the steady uniform stretching leads to equal and opposite forces along x-axis; hence the sheets will be stretched by fixing the origin.
. Here, the term y is the normal coordinate with respect to the stretching sheet. Practically the steady uniform stretching leads to equal and opposite forces along x-axis; hence the sheets will be stretched by fixing the origin.
The following assumptions are made before getting into more mathematical formulations. Assume the temperature at stretching surface as a function of x (see Equation (5)), ambient temperature T as constant and at the sheet nano particle fraction C as a constant with a value . Now assume that the sheet is extended by stretching with a nonlinearity parameter n along with a velocity of
. Now assume that the sheet is extended by stretching with a nonlinearity parameter n along with a velocity of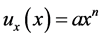 . Here x is the stretching surface coordinate where the measurement is being taken place.
. Here x is the stretching surface coordinate where the measurement is being taken place.
Now consider a nanofluid is flowing at 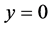 and consider fluid to be under the influence of electrical conduction because of the magnetic field
and consider fluid to be under the influence of electrical conduction because of the magnetic field , which is normal to stretching sheet. Make a note that at stretching surface the
, which is normal to stretching sheet. Make a note that at stretching surface the 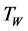 (wall temperature) and
(wall temperature) and 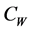 are considered to be constant. The ambient value of temperature
are considered to be constant. The ambient value of temperature 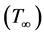 and nanoparticle fraction
and nanoparticle fraction 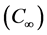 are denoted when y tends to infinity. The physical system considered for this study included for nano-technical fabrication and thermal material processing. In the Figure 1, coordinate system and flow models are shown and governing equations are given below:
are denoted when y tends to infinity. The physical system considered for this study included for nano-technical fabrication and thermal material processing. In the Figure 1, coordinate system and flow models are shown and governing equations are given below:
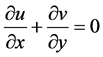 (1)
(1)
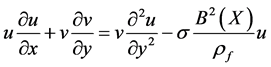 (2)
(2)
 (3)
(3)
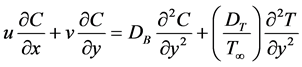 (4)
(4)
The boundary conditions for parameters velocity, temperature and nano-particle fraction are given below:
 (5)
(5)
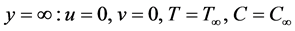 (6)
(6)
where,
u and v are the velocity components in x and y directions,
a is acceleration of components.
Thermal Diffusivity 
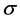 is electrical conductivity,
is electrical conductivity,
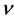 is the kinematic viscosity,
is the kinematic viscosity,
![]() is the density,
is the density,
![]()
Figure 1. The Physical model and corresponding coordinate systems.
![]() is the Brown Diffusion Coefficient,
is the Brown Diffusion Coefficient,
![]() is the thermo phoresis diffusion coefficient.
is the thermo phoresis diffusion coefficient.
However,
![]()
The ![]() is the ratio between effective heat capacity of the nanoparticle material and fluid.
is the ratio between effective heat capacity of the nanoparticle material and fluid.
Here,
c is volumetric volume coefficient,
![]() is density of particles,
is density of particles,
C is rescaled volume fraction of nanoparticles,
R is radiation parameter.
Now assume variable magnetic field ![]() is in the for
is in the for![]() .
.
Using Rosseland approximation for radiation, we can write
![]() (7a)
(7a)
where ![]() is the absorption coefficient,
is the absorption coefficient, ![]() is the Stefan-Boltzman constant. Assuming the temperature difference within the flow is such that
is the Stefan-Boltzman constant. Assuming the temperature difference within the flow is such that ![]() may be expanded in a Taylor series about
may be expanded in a Taylor series about ![]() and neglecting higher orders we get
and neglecting higher orders we get![]() .
.
Hence, Equation (7a) becomes
![]() (7b)
(7b)
Hence
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,![]() . (7)
. (7)
where ![]() represents stream functions and is defined as
represents stream functions and is defined as![]() ,
, ![]() so that
so that
Equation (1) is satisfied identical. The governing Equations (2)-(4) or reduced by Equations (7).
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
The transformed boundary conditions are
![]() (11)
(11)
Here, primes in the above equation represent the differentiation with respect to η, which is known to be an involved physical parameter and it is defined as follows:
![]() (12)
(12)
Here,
![]() is Prandtl number,
is Prandtl number,
![]() is the Lewis number,
is the Lewis number,
![]() is the Brownian motion parameter,
is the Brownian motion parameter,
![]() is the thermophoresis parameter,
is the thermophoresis parameter,
![]() is magnetic parameter,
is magnetic parameter,
![]() is the Eckert number,
is the Eckert number,
![]() is the porous term,
is the porous term,
![]() is the radiation parameters.
is the radiation parameters.
This boundary value problem is reduced to the classical problem of flow and heat and mass transfer due to a stretching surface in a viscous fluid when ![]() and
and ![]() in Equations (9) and (10).
in Equations (9) and (10).
In this study the quantities of practical interest are listed below:
![]() (13)
(13)
![]() is local skin friction,
is local skin friction,
![]() is Nusselt Number,
is Nusselt Number,
![]() is Sherwood Number.
is Sherwood Number.
The heat and mass fluxes ![]() at different surfaces for the thermal conductivity (k) is given by
at different surfaces for the thermal conductivity (k) is given by
![]() (14)
(14)
Substituting Equation (7) into Equations (13) and (14), we obtain
![]() ,
,
where ![]() is the local Reynolds number.
is the local Reynolds number.
3. Results and Discussion
Exact analysis for the reduced Equations (8)-(11) are not possible as they are nonlinear and coupled. However using Keller-Box method these problems can be evaluated for different values and parameters such as Pr, Nb, T and Le. Various effects are investi-
gated in this paper such as dimensionless velocity, temperature, skin function, mass transfer and rate of heat.
Some of the principal steps of Keller Box methods are listed below:
1) Reducing higher order ODEs to the first order ODEs
Let ![]() and
and ![]()
![]() and
and ![]()
Let ![]()
![]()
Let ![]()
![]()
In the following steps only first ODE statement will be considered for further steps to follow using Keller Box method.
2) First order ODEs are written into difference equations by using central differencing schemes
Let us apply the central differential equation for ![]()
![]()
![]()
3) Using the Newtons method to linearizing the difference equation for extending it into vector form
![]()
![]()
4) And finally using block elimination method the system equations are solved to draw the corresponding matrices.
MATLAB software is used to solve the differential equations numerically. This software is very efficient for using with Keller Box method.
Various comparisons are presented in Table 1 to validate the proposed method with respect to previous method for the equations ![]() and
and![]() . This comparisons resulted to be excellent and are found to be excellent. At the same time various effects due to magnetic and viscous parameters are shown in the Table 2. The
. This comparisons resulted to be excellent and are found to be excellent. At the same time various effects due to magnetic and viscous parameters are shown in the Table 2. The ![]() is decreasing with respect to M, Ec, n and Lewis numbers. However
is decreasing with respect to M, Ec, n and Lewis numbers. However ![]() also is a decreasing function of with respect to parameters M, n and Nt but is found to be increasing with respect to Pr, Ec and Le. Increase in Le means the fluid is more viscous as similar to radiation parameter (R) which in turn increases the rate of mass transfer and raise in Le reduces the heat transfer.
also is a decreasing function of with respect to parameters M, n and Nt but is found to be increasing with respect to Pr, Ec and Le. Increase in Le means the fluid is more viscous as similar to radiation parameter (R) which in turn increases the rate of mass transfer and raise in Le reduces the heat transfer.
The magnetic parameter (M) effect is shown in Figure 2, in which the tangential velocity of fluid is decreasing with a raise in the values of magnetic field. However Lorentz forces is introduced in an electrically conducting fluid due to the interrelation between
![]()
Table 1. Comparison of skin friction coefficient, Nusselt and Sherwood number for various Values of Ec when Pr = 10, n = 10, Le = 10 and Nt = 0.3.
both magnetic and electrical fields. The Lorentz force acts against the flow when magnetic field is applied normal to the direction. In such scenarios the resistive forces will slow down.
The positive changes in M allow increasing the temperature within the boundary layer as shown in Figure 3. These profiles cannot be observed in the graph due to the limitations of boundary layer. The temperature profiles are plotted for different values of M.
The influence of M, nonlinear stretching parameter n on dimensionless, and nanoparticle concentrations are shown in Figure 4. The increase in M will enhance the dimensionless concentration profiles can be observed in Figure 4. Lorentz forces are resistive in nature opposing the fluid motion and hence the result is the production of heat. In such scenarios, in the magnetic field, the thermal boundary layer and nanoparticle volume fraction boundary layers thickness will increase. The nonlinear stretching
![]()
Figure 3. The temperature profiles for M.
parameter is slightly negligible for the variation of nanoparticle concentration. Note that these parameters are negligible for both positive and negative values of n.
The effect of R for fixed values of other parameters the dimensionless concentrations
![]()
Figure 4. The temperature profiles for R.
![]()
Figure 5. The concentration profiles for R.
are shown in Figure 5. Inhibit nanoparticle pieces diffusion is observed in Figure 5 for the large values of R. However, there will be heavy reduction in concentration boundary layer thickness.
Behaviour of temperature with respect to different values of Pr numbers are shown in Figure 6. This shows the decrease in velocity with the raise in Pr which leads to a decrease in the thermal boundary layer thickness. In simple this can be understood due to the raise in thermal conductivity for small values of Pr and hence the heat will be
diffused away from the heated surface as compared with the high values of Pr. Therefore the smaller Pr number due to thermal boundary layer leads to a thicker and hence the transferred heat will be reduced.
The temperature profiles for different values of Ec are plotted in Figure 7. The increase in the values of Ec is due to the increases in temperature within the boundary layer.
The effect of Ec on dimensionless concentration for various fixed values of other parameters is shown in Figure 8. The larger values of Ec suppress concentration profiles and hence inhibit nanoparticle species diffusion is observed. However there is a much greater reduction in concentration boundary layer thickness.
For the plot between behaviour of temperature and different value of Le are shown in Figure 9 shows that the increase in Le results to a decreasing velocity due to which thermal boundary layer thickness will be decreasing so that less average temperature within boundary layer is observed. Reasons for small values of Le allow the thermal conductivity of the fluid to increase. Hence it allows the heat to diffuse rapidly from the heated surface for high values of Le.
Effect of Le on dimensionless concentration for various fixed parameters is shown in Figure 10. Larger values of Le suppress concentration profiles and a greater reduction will be seen in the concentration of boundary layer thickness.
![]()
Figure 7. The temperature profiles for Ec.
![]()
Figure 8. The concentration profiles for Ec.
Behaviour of temperature with respect to different values of Nb are showin in Figure 11. The increasing Nb values results in a decreasing velocity. It also results for a decrease in the thermal boundary layer thickness and hence reduces the average temperatures within the boundary layers. The reason behind such scenario lies in the smaller
![]()
Figure 9. The temperature profiles for Le.
values of Nb will allow to an increase in thermal conductivity of fluids so that heat will be diffused from heated surface rapidly for higher values of Nb. Hence for smaller Nb the thermal boundary layer is thicker and rate of heat transfer will be reduced.
![]()
Figure 12. The concentration profiles for Nb.
Effect of Nb for dimensionless concentration for various fixed values of other parameters is observed in Figure 12. Here for higher values of Nb suppress the concentration profile and hence greater reduction in the thickness of the concentration boundary
layer.
The Nt on temperature and concentration profiles are shown in Figure 13. In this the temperature profile increases the concentration profile due to Nt inhibits the fluid for not to move freely in the boundary layer, which in turn leads the flow to increase
the thickness of thermal boundary layer.
Influence of Nt and n on dimensionless and nanoparticle concentrations are shown in Figure 14 and the dimensionless profiles are observed to be enhancing with the
increase of Nt. However Lorentz force opposes the fluid motion hence the heat is produced. Due to such conditions thermal boundary and nanoparticle volume fraction boundary layer thickness will become thicker for strong Nt.
4. Conclusion
In this paper, various similarity solutions for viscous flow and heat transfer of nanofluids on nonlinear streached sheets under the influence of thermal radiation are shown in the results. However, similar solutions are depending on Pr, Le, M, n, Nb, T and Nt. The graphical representations of various governing parameters are obtained in different conditions to draw the importance of thermal radiation and some of the featured observations of the findings are listed below:
・ The velocity is decreasing with the increase in temperature.
・ Ec will increase proportionally with Eckert number.
・ The increase in M will lead to a decrease in velocity parameter.
・ The temperature will increase due to an increase in R.
・ The concentration will decrease due to an increase in R.
Acknowledgements
I thank MHRD, Govt. of India for supporting my work through UGC-BSR Fellowship.