1. Introduction
The Assignment Problem (AP), also known as the maximum weighted bipartite matching problem, is a special type of Linear Programming Problem (LPP), in which the objective is to assign number of jobs to number of workers at a minimum cost (time). The mathematical formulation of the problem suggests that this is an integer programming problem and is highly degenerated. All the algorithms developed to find optimal solution of transportation problem are applicable to assignment problem. However, due to its highly degeneracy nature, a specially designed algorithm widely known as Hungarian method proposed by Kuhn [1] is used for its solution. The assignment problem, also known as the maximum weighted bipartite matching problem, is a widely-studied problem applicable to many domains, specifically for maximization of output or minimization of cost. It can be stated as follows: given a bipartite graph made up of two partitions V and U, and a set of weighted edges E between the two partitions, the problem requires the selection of a subset of the edges with a maximum sum of weights such that each node 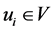 or
or 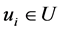 is connected to at most one edge. The problem may also be phrased as a minimization problem by considering, instead of edge weights
is connected to at most one edge. The problem may also be phrased as a minimization problem by considering, instead of edge weights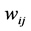 , a set of non-negative edge costs,
, a set of non-negative edge costs, 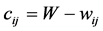 , where W is at least as large as the maximum of all the edge weights. It can also be stated as: how to determine the best possible assignment of workers to jobs, such that the total ratings are maximized [2] .
, where W is at least as large as the maximum of all the edge weights. It can also be stated as: how to determine the best possible assignment of workers to jobs, such that the total ratings are maximized [2] .
2. Related Works
Franses and Gerhard [3] studied an assignment problem particular to the personnel scheduling of organisations such as laboratories. Here the authors have to assign tasks to employees. The authors focused on the situation where this assignment problem reduces to constructing maximal matchings in a set of interrelated bipartite graphs. The authors described in detail how the continuity of tasks over the week is achieved to suit the wishes of the planner. Turkish Armed Forces assign thousands of personnel to vacant positions every year, and want to utilize the personnel to a maximum extent by assigning the right person to the right job, while taking into consideration the hierarchy constraint, Cimen [4] .
Toroslu and Arslanoglu [5] , presented variations of the standard assignment problem with matching constraints by introducing structures in the partitions of the bipartite graph, and by defining constraints on these structures.
Naveh et al. [6] presented a novel solution designed to bridge the gap between the need for high-quality matches and the need for timeliness. By applying constraint programming, a subfield of artificial intelligence, the authors dealt successfully with the complex constraints encountered in the field and reach near-optimal assignments that take into account all resources and positions in the pool.
Katta and Jay [7] presented the problem of allocating a set of indivisible objects to agents in a fair and efficient manner.
Zhang and Bard [9] studied a multi-period assignment problem that arises as part of a weekly planning problem at mail processing and distribution centres.
2.1. The Assignment Problem
Suppose we have n resources to which we want to assign to n tasks on a one-to-one basis. Suppose also that we know the cost of assigning a given resource to a given task. We wish to find an optimal assignment?one which minimizes total cost.
2.2. Mathematical Model
Let 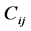 be the cost of assigning the ith resource to the jth task. We define the cost matrix to be the n × n matrix
be the cost of assigning the ith resource to the jth task. We define the cost matrix to be the n × n matrix
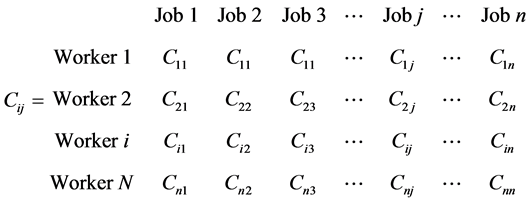
An assignment is a set of n entry positions in the cost matrix, no two of which lie in the same row or column. The sum of the n entries of an assignment is its cost. An assignment with the smallest possible cost is called an optimal assignment. The assignment problem can be written mathematically as:
Minimize
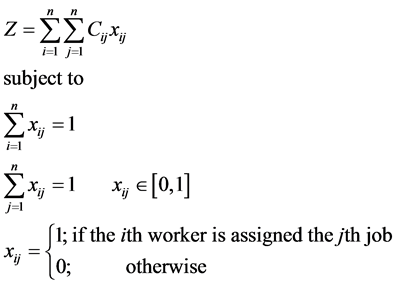
2.3. Hungarian Method
The following algorithm applies the above theorem to a given n × n cost matrix to find an optimal assignment.
Step 1: Subtract the smallest entry in each row from all the entries of its row.
Step 2: Subtract the smallest entry in each column from all the entries of its column.
Step 3: Draw lines through appropriate rows and columns so that all the zero entries of the cost matrix are covered and the minimum number of such lines is used.
Step 4: Test for Optimality:
i) If the minimum number of covering lines is n, an optimal assignment of zeros is possible and we are finished.
ii) If the minimum number of covering lines is less than n, an optimal assignment of zeros is not yet possible. In that case, proceed to Step 5.
Step 5: Determine the smallest entry not covered by any line. Subtract this entry from each uncovered row, and then add it to each covered column. Return to Step 3.
2.4. Penalty method (Proposed Heuristic Method)
The algorithm for n × n cost matrix using the proposed heuristic method is as shown below.
・ Compute row/column penalties by subtracting the least entry from the next least;
・ Select the two maximum penalties from the row or column penalties. Use the maximum penalties to select the least cost among these penalties.
・ Cross-out the row and column on which the minimum cost is located
・ If there is a tie of the minimum cost from the same row or the same column, choose the cost of the third maximum penalty
・ Break ties arbitrary when there is a tie on the cost from maximum row and column penalty
・ If the least cost emanating from maximum penalty has its corresponding row or column penalty as zero, choose the least cost from the next maximum penalty.
・ Repeat bullet two
・ Stopping criteria: stop when all rows and columns have been crossed out.
3. Comparative Results Using the Hungarian and the Proposed Method
The following examples give the optimal results from the two methods and their computing time. The two algorithms were coded using C++ on
4. Results and Conclusion
Test computation from a randomly generated numbers with our proposed heuristic method gave comparable results compared with that of Hungarian method. However, the computational time and convergence rate of the proposed method showed much less time than that of the Hungarian method.