Interaction Energy between an Atomic Force Microscope Tip and a Charged Particle in Electrolyte ()
1. Introduction
An open problem of current scientific and technological interest is the theoretical prediction of the force between an Atomic Force Microscope (AFM) probe and a charged particle, in particular when both are immersed in an electrolytic environment [1] . The main interest of this problem comes from the need to understand the electrostatics of biological matter, a problem in which water is inherently present [2] . In addition, AFM has become the de facto metrological tool to probe organic and inorganic matter from the micron down to the nanometer length scales [3] . The tip comprises the sensing element of the AFM and, at its apex ranges in size from microns to nanometers, thus the ability of the AFM to probe those length-scales. When the AFM tip is immersed in an electrolyte, it can gain surface charge due to pH, and also can develop a diffuse charge layer due to the presence of ions in solution [4] . Thus we see a natural conceptual connection between AFM measurements in liquid and colloidal science, whereby the interest is in the interaction between colloidal particles and their corresponding stability. Therefore, although our interest is in AFM in liquid, the results obtained here are readily usable in colloidal systems. We focus here in a liquid system in which 1- 1000 nm particles are submerged in an ionic solution. Colloidal systems comprise one of the primary types of mixtures in chemistry. One of the central problems in colloids is their stability [5] , that is, under known conditions, such as concentration; will the system coagulate or remain indefinitely stable?
The stability of colloids is indeed known to depend on the presence of charge at their surfaces [6] ; the electrical double layer controls electrostatic stabilization. When particles approach each other, the interaction leads to the rearrangement of charges in the ambient liquid, outside of the colloidal particles. For instance, these interactions could be determined by the surface charge on the particles and electrolyte concentration. The stability of colloidal systems is interesting conceptually, and critical for industrial appli- cations. In chemistry, there are different types of colloidal systems such as solid-liquid dispersions (suspensions), liquid-liquid dispersions (emulsions) and gas-liquid dispersions (foams). Paints, milk, proteins as well as fog are some of the daily examples of colloids [7] [8] .
Mathematically, the stability depends on the details of the pair-wise energy as a function of separation of colloidal particles [9] . The valleys of such function determine the separations of the possible equilibrium. One approach to obtain that energy is to first solve the Poisson-Boltzmann (PB) equation, whose solution gives the charge density and electrostatic potential in the liquid surrounding the colloidal particles [10] . In general, PB equation provides the distribution of the electric potential in solution with charged ions present. This distribution, in turn, provides information to determine how the electrostatic interactions will affect colloidal forces. PB is a nonlinear second-order partial differential equation which has an exact known solution only in one dimension. In higher dimensions, PB equation is commonly solved by numerical analysis. Alternatively, if the colloidal particle charge or voltage is not high, the PB equation can be linearized, in which case solutions for spherical [11] and cylindrical [12] geometries have also been obtained. For the particular geometry of sphere-plane, useful to study charge transfer in scanning tunneling microscopy and forces in atomic force microscopy, there have been analytical and numerical approaches to the nonlinear PB equation in three dimensions [13] [14] [15] [16] . Here, we present a method to tackle the full nonlinear PB equation in three-dimensions for interacting particles. The method is analytical, based on the choice of a parametric trial family of functions. While the method is approximate, its analytical nature should provide conceptual insight into the problem.
The exact PB nonlinear equation in 3D is not amenable to analytical solutions even for a single colloidal particle in the electrolyte. We here consider the problem of two interacting particles by introducing an ansatz for the charge density function and corresponding electrostatic potential parametrically; the variational method is then used to minimize the PB functional with respect to the parameters.
2. Electrostatics Potential Produced by a Pair of Colloids
Figure 1 shows schematics of the system of interest. Two charged spherical colloidal particles of unit diameter are separated by a distance d.
The PB equation is typically obtained by combining Poisson’s equation [17] and the Boltzmann factor [18] for the distribution of electrostatic energies at a given temperature. Thus Poisson’s equation gives the relationship between the electrical potential 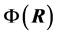 and the charge density
and the charge density 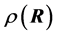 at location
at location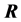 ,
,
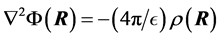 (1)
(1)
with 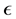 is the dielectric constant of the surrounding fluid. On introducing the Boltz- mann distribution of ions, the non-linear PB equation is obtained,
is the dielectric constant of the surrounding fluid. On introducing the Boltz- mann distribution of ions, the non-linear PB equation is obtained,
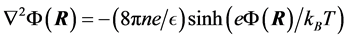 (2)
(2)
where n is the ion bulk concentration of electrolyte, T is the absolute temperature, e the ion charge magnitude of anions and cations, and kB is Boltzmann’s constant.
Equation (2) is converted into dimensionless form [2] by defining the dimensionless electrostatic potential 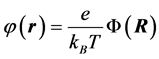 and the dimensionless position vector
and the dimensionless position vector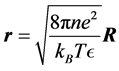 ,
,
![]()
Figure 1. Two colloidal particles (large, blue) separated by a distance d. The unit of length throughout the paper is the particles diameter, or the AFM tip diameter. The small red particles represent the ions dissolved in water and are treated as a continuum in the Poisson-Boltzmann approach. These ions could be different, we show them here with the same color for graphical simplicity.
 (3)
(3)
where 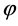 now represents the dimensionless electrostatic potential, and the Laplacian in Equation (3) is with respect to
now represents the dimensionless electrostatic potential, and the Laplacian in Equation (3) is with respect to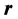 . Since n has unites of inverse volume, and
. Since n has unites of inverse volume, and 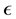 is
is
the absolute dielectric constant, 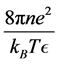 has units of inverse area.
has units of inverse area.
Equation (3) can be derived from a variational principle, by applying Euler-Lagrange to the action
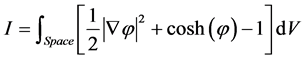 (4)
(4)
where V is volume. The minimum of I occurs for the function φ that satisfies the Euler-Lagrange equation, which gives rise Equation (3).
Taking z as the axis that joins the centers of the two colloidal particles, and due to the axial symmetry of the problem, we rewrite the action in cylindrical coordinates as
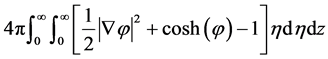 (5)
(5)
where η is the radial polar coordinate in the xy plane, while the angular polar integration is readily performed and gives 2π. The additional factor of 2 comes from integrating z in half space and multiplying by 2 due to mirror symmetry. To make progress, we propose the following ansatz for the density and corresponding electrostatic potential which depends on the parameter k,
 (6)
(6)
where 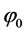 is the Dirichlet boundary condition, d is the center-to-center separation between the two spherical colloids and k is a constant that can be interpreted as an inverse Debye length times the radius of the interacting particles. The intuitive justifications for the functional form are 1) its exponential decay typical of ionic screening, 2) that proper boundary conditions
is the Dirichlet boundary condition, d is the center-to-center separation between the two spherical colloids and k is a constant that can be interpreted as an inverse Debye length times the radius of the interacting particles. The intuitive justifications for the functional form are 1) its exponential decay typical of ionic screening, 2) that proper boundary conditions ![]() are achieved at the surface of the colloids, and 3) that as
are achieved at the surface of the colloids, and 3) that as![]() , the electrostatic potential between the two colloids tends to zero. Figure 2 shows a contour plot of the potential around the colloidal particles for a choice of k.
, the electrostatic potential between the two colloids tends to zero. Figure 2 shows a contour plot of the potential around the colloidal particles for a choice of k.
To emphasize, this choice of potential is dictated first by the fact that the potential must rapidly approach its bulk value away from the spheres, and second by the fact that the electrostatic potential must have a constant value at the surface of the colloidal particles (Dirichlet boundary conditions).
To find the sought solution to the original PB equation (Equation (3)), we minimize the PB action functional with respect to the parameter k. For fixed potential φ0 and fixed separations d, we find the constant k (i.e. minimum point k = k(φ0, d)) for the proposed φ(x, y) that minimizes the action.
As Figure 3 shows, for small separations, the data suggests that there is an approximately linear relationship between the best constant kbest, and the separation d for each
![]()
Figure 2. Contour plot of![]() . The potential is constant
. The potential is constant ![]() at the surfaces of the particles, becomes spherical far away while decaying to zero.
at the surfaces of the particles, becomes spherical far away while decaying to zero.
boundary condition φ0. It leads us to further investigate the relationship between the linear relationship and the boundary condition φ0.
We obtain polynomial approximations for the functions that relate the linear parameters (that are the slopes and η-intercepts) and the boundary conditions (as shown in Figure 4(a) and Figure 4(b)).
Moreover, for large separations between the colloidal particles, the best constant k converges to 0.1 for all of the boundary conditions φ0. This should be a universal feature regardless of the model used since at large separations we should obtain a simple superposition the potential around single spheres.
The functional forms for the kbest allow us to write a simple function as follows (Figure 5).
![]() (7)
(7)
where A(φ) is the polynomial approximation between the linear parameter-η-intercepts and φ0, B(φ) is the polynomial approximation between the other linear parameter-slope and φ0, and d is the center-to-center separation between the colloids.
3. Colloid Interaction Energy
Since the charge is distributed in the whole space that surrounds the colloidal particles, we have the energy as a function of separation d [13]
![]() (8)
(8)
where to recall ρ is density and φ is voltage, which are now known from the previous section. For each boundary condition, the integral in (8) is performed for the corresponding optimal value of k.
Equation (8) then provides the sought sphere-sphere energy-separation curves. The computed results are shown in Figure 6. Based on the shape of the curves, we now can draw conclusions regarding the stability properties predicted by this theory.
4. Conclusions
Figure 6 is the main quantitative result of this work and it shows that for all boundary conditions φ0 the particles attract each other at small separations. This is consistent with all the published experimental literature [19] . In addition, our results show that for large φ0 the energy decreases monotonically giving rise to repulsion at large separations. While, for small φ0 there are plateaus that suggest the existence of secondary minima. [15] For all values of φ0 there are local minima at distances larger than 30, but they cannot be expected to represent experimental behavior since they correspond to distance too large compared to the size of the particles. We also notice that the peak positions of the energy curves shift to larger distances as φ0 increases, as expected. Finally the behavior of the screening parameter as shown in Figure 5 shows a strong dependence with distance and reducing its value by more than 50%. This has been observed in experimental measurements [15] .
For the AFM community, these results are useful in comparing experimental forces with the derivative of the curves in Figure 6. Although the results presented here are limited to particles of the same size, it is clear that the extension of two different radii amounts to adding a second parameter to Equation (6). With that modification, and by choosing the proper theoretical curve, one can infer the charge of the particle interacting with the AFM tip.
![]()
Figure 6. The energy-separation curves for φ0 from 1 to 8.
Acknowledgements
Funding for this project comes from the National Science Foundation grant #CHE- 1508085.