A Model of Perfect Pediatric Vaccination of Dengue with Delay and Optimal Control ()
1. Introduction
Dengue fever and dengue hemorrhagic fever are the vector-borne diseases which transcend international borders as the most important arboviral diseases currently threatening human populations. The research found that more than approximately 50 million people are affected by dengue disease each year [1] . The virus of dengue is transmitted to humans by mosquitoes, mostly the Aedes aegypti and Aedes albopictus. There are at least four different serotypes of dengue viruses, therefore people might be infected with dengue disease more than once [2] . Up to present, the only available strategy against dengue still controls the vectors. Despite combined community participation with vector control, together with active disease surveillance and insecticides, whereas, the example of successful dengue prevention and control on a national scale are little. Besides, in the wake of the level of resistance of Aedes aegypti and Aedes albopictus to insecticides increasing, the intervals between treatments are shorter, moreover, as a result of the high costs for development and registration and low returns, only few insecticide products are available in the markets [3] . Considering these conditions, vaccination could be more effectiveness and security to protect dengue viruses.
In 1760, the Swiss mathematician Daniel Bernoulli published an investigation on the impact of immunization with cowpox. From then on, the means of protecting figures from infection through immunization begin to be widely used; in addition, the method has already successfully decreased both mortality and morbidity [4] . Based on data from WHO, the worldwide majority of patients suffering from Dengue fever are children. Meanwhile, immunization could be including a category, i.e., pediatric vaccination. There are a lot of pediatric vaccines have already protected multiple childhood diseases successfully, such as Calmette’s vaccine, hepatitis B vaccine and measles vaccine, etc. In view of the fact that many childhood diseases have very low immunity-loss rate, considering the conditions of perfect pediatric vaccination are reasonable.
Since the 1940s, dengue vaccines have been under development. But industry interest languished throughout the 20th century owing to the limited appreciation of global disease burden and the potential markets for it. In recent years, however, with the increase in dengue infections, the development of dengue vaccines has amazingly accelerated, as well as the prevalence of all four circulating serotypes. It became a serious concern for faster development of a vaccine [5] . To guide public support for vaccine development in both industrialized and developing countries, economic analysis are conducted, including previous cost-effectiveness study of dengue [6] [7] . The cost of the disease burden with possibility of making a vaccination campaign are compared by the authors of these analytical works; when compared two situations, they consi- der that the way of dengue intervention―dengue vaccines has a potential economic benefit.
On the other hand, there are three successive aquatic juvenile phases (egg, larva and pupa) and one adult pupa for the life cycle of the mosquitoes. It is large compared the duration from the egg to the adult (1 - 2 weeks) with the average life span (about 3 weeks) of an adult mosquito. The size of the mosquito population is strongly affected by temperature. The number of female mosquitoes changes accordingly due to seasonal variations. When the size of the mosquito population increases during the favorable periods, the dengue virus infection among individuals also increases, therefore the incidence for humans’ increases. Then it is vital to consider the maturation time of mosquitoes, the length of the larval phase from egg to adult mosquitoes, and the impact on the transmission of dengue virus.
Based on above-mentioned conditions, a dengue dynamical model with maturation delay and pediatric vaccination is proposed to consider the effects of maturation delay and pediatric vaccination for the transmission of dengue between mosquitoes and human. The remaining parts of this paper are organized as follows. A form of vaccination model is formulated: a perfect pediatric vaccination model, in the next Section. And the stability of equilibria of the model is analysed in Section 3. In Section 4, the optimal control strategy of the disease is discussed. Finally, the numerical simulation is performed in Section 5.
2. Model Formulation and Preliminaries
Dengue can be a serious candidate for a type of vaccination which is much focus on vaccinating newborns or very young infants. It parallels many potentially human infections, such as measles, rubella, polio. In this section, we propose a SVIR model in which a continuous vaccination strategy is considered, and a proportion of the newborn 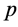 (
(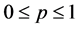 ) was by default vaccinated. We also assume that the permanent immunity acquired through vaccination is the same as the natural immunity obtained from infected individuals eliminating the disease naturally.
) was by default vaccinated. We also assume that the permanent immunity acquired through vaccination is the same as the natural immunity obtained from infected individuals eliminating the disease naturally.
The mathematical model can be described as:
 (1)
(1)
where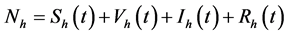 , and the meanings of other model parameters and the schematic diagram of model (1) see Table 1 and Figure 1, respectively.
, and the meanings of other model parameters and the schematic diagram of model (1) see Table 1 and Figure 1, respectively.
The initial condition of model (1) is given as
 (2)
(2)
where  and
and  are positive continuous functions for
are positive continuous functions for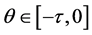 .
.
Firstly, it follows from model (1) that the total number of adult female mosquitoes satisfies the following equation
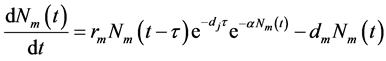 (3)
(3)
With initial condition
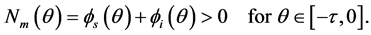 (4)
(4)
Letting
 (5)
(5)
![]()
Table 1. Parameter values for model (1).
![]()
Figure 1. Schematic diagram of the basic model (1).
it follows that 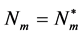 is a unique positive equilibrium for the mosquito of equation (3), and it exists if and only if
is a unique positive equilibrium for the mosquito of equation (3), and it exists if and only if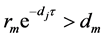 . Defining
. Defining
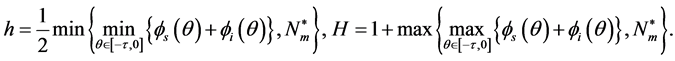
The following theorem describes the global asymptotic behavior of equation (3).
Theorem 1. For model (3) with the initial condition (4), the solution  is positive for any finite time
is positive for any finite time . Further,
. Further,
(i) If![]() , then the solution
, then the solution ![]() is bounded and the trivial equilibrium
is bounded and the trivial equilibrium ![]() is globally asymptotically stable with respect to the positive initial data.
is globally asymptotically stable with respect to the positive initial data.
(ii) If![]() , then
, then ![]() for any
for any![]() . Moreover, there is a positive equilibrium
. Moreover, there is a positive equilibrium ![]() that is globally asymptotically stable.
that is globally asymptotically stable.
The process of proofing is absolutely same as Theorem 1 in Reference [10] , omitted.
Now, define two threshold values
![]()
Assuming that the vaccine is perfect, which means that it confers life-long protection. For model (1), we can get two nontrivial disease-free equilibria and a endemic equilibrium. That is, the disease-free equilibrium without mosquitoes![]() , the disease-free equilibrium with mosquitoes
, the disease-free equilibrium with mosquitoes ![]() for
for ![]() and
and![]() , the endemic equilibrium
, the endemic equilibrium ![]() for
for ![]() and
and![]() , where
, where
![]()
3. Stability of Equilibria
Firstly, on the globally asymptotical stability of disease-free equilibrium without mosquito![]() , we have the following theorem.
, we have the following theorem.
Theorem 2. If![]() , then model (1) has a unique disease-free equilibrium without mosquitoes
, then model (1) has a unique disease-free equilibrium without mosquitoes ![]() and which is globally asymptotically stable. Further,
and which is globally asymptotically stable. Further, ![]() is unstable for
is unstable for![]() .
.
Proof. It obvious that ![]() according to Theorem 1. So we merely proof that
according to Theorem 1. So we merely proof that![]() ,
, ![]() , and
, and ![]() .
.
For the first equation of model (1) we have![]() , Consider an auxiliary system
, Consider an auxiliary system
![]() (6)
(6)
Obviously, it is easy to obtain that system (6) has a unique positive equilibrium![]() , which is globally asymptotically stable.
, which is globally asymptotically stable.
By comparison principle, ![]() , which implies that for small enough
, which implies that for small enough![]() , there exists a constant
, there exists a constant ![]() such that
such that![]() , for all
, for all![]() .
.
Due to![]() , then for small enough
, then for small enough![]() , there is constant
, there is constant ![]() such that
such that![]() , for all
, for all![]() . Letting
. Letting ![]() and
and![]() , then for
, then for![]() ,
, ![]() and
and![]() , for all
, for all![]() .
.
From the third and the forth equation of model (1) we get
![]()
Consider the comparison differential equation
![]() (7)
(7)
It is easy to obtain that ![]() is the solution of (7) for small enough
is the solution of (7) for small enough![]() , which is globally asymptotically stable.
, which is globally asymptotically stable.
By comparison principle,![]() . According to the nonnegativeness of
. According to the nonnegativeness of ![]() and
and ![]() with the initial condition (2), we obtain that
with the initial condition (2), we obtain that ![]() . Finally, we can easily obtain the results of
. Finally, we can easily obtain the results of ![]() and
and![]() . The proof is complete.
. The proof is complete.
On the stability of disease-free equilibrium with mosquitoes, linearizing model (1) about ![]() yields the characteristic equation
yields the characteristic equation
![]() (8)
(8)
Similarly, as for the endemic equilibrium![]() , we can clearly see in each component’s expression of
, we can clearly see in each component’s expression of ![]() that it is positive when
that it is positive when![]() . It is obvious that the stability of component
. It is obvious that the stability of component ![]() and the stability of other components are not interrelationship, so we omit the
and the stability of other components are not interrelationship, so we omit the ![]() when we linearise the model (1) about
when we linearise the model (1) about ![]() to simplify the characteristic equation. The corresponding characteristic equation for
to simplify the characteristic equation. The corresponding characteristic equation for ![]() can be written as
can be written as
![]() (9)
(9)
Obviously, the study of solving these transcendental equations of (8) and (9) is out of the scope of this one. Therefore, we give the stability of ![]() by other analytical skill and perform numerical stimulations in the stability of the endemic equilibrium
by other analytical skill and perform numerical stimulations in the stability of the endemic equilibrium![]() .
.
Theorem 3. Supposing that![]() . If
. If
![]() (10)
(10)
then model (1) has a unique disease-free equilibrium with mosquitoes ![]() and which is globally asymptotically stable. Further,
and which is globally asymptotically stable. Further, ![]() is unstable for
is unstable for ![]() and model admits a unique endemic equilibrium
and model admits a unique endemic equilibrium![]() .
.
Proof. From the sixth equation of model (1) we get ![]() By integrating above inequality from
By integrating above inequality from ![]() to
to![]() , we obtain
, we obtain![]() . Then
. Then
![]()
Consider another auxiliary system
![]() (11)
(11)
it is obvious that the equilibrium ![]() always exists. Linearizing the model (11) about
always exists. Linearizing the model (11) about ![]() yields the characteristic equation
yields the characteristic equation
![]() (12)
(12)
where![]() ,
, ![]() ,
, ![]() and
and![]() .
.
To obtain two negative solutions about (12), require that
![]()
Then only requires to satisfies that![]() . So, we obtain the finally stable condition of model (11). That is
. So, we obtain the finally stable condition of model (11). That is
![]()
According to above discussion and comparison principle we know that ![]() and
and ![]() for
for ![]() and
and![]() . In addition, in the light of Theorem 1, we get
. In addition, in the light of Theorem 1, we get![]() .
.
As for the stability about other variations of model (1), they are absolutely same as Theorem 2, omitted.
Remark 1. In fact, q is small enough since the vertical transmission of Dengue virus in mosquitoes is rare. Therefore, ![]() , and
, and ![]() for
for![]() .
.
4. Optimal Vaccination
In this section, the vaccination of model (1) is seen as a control variable to reduce or even eradicate the disease. Let p be the control variable: ![]() denotes the percentage of newborns that one decides to vaccinate at time t. The main aim is to research the optimal vaccination strategy, considering both the treatment costs of infected individuals and the vaccination costs. The objective is to
denotes the percentage of newborns that one decides to vaccinate at time t. The main aim is to research the optimal vaccination strategy, considering both the treatment costs of infected individuals and the vaccination costs. The objective is to
![]() (13)
(13)
where ![]() and
and ![]() representing the weights of the costs of treatment of infected people and vaccination, respectively, and they are both positive constants. We solve the problem using optimal control theory. Consider the set of admissible control functions
representing the weights of the costs of treatment of infected people and vaccination, respectively, and they are both positive constants. We solve the problem using optimal control theory. Consider the set of admissible control functions ![]()
We have the following theorem on the existence of optimal vaccination.
Theorem 4. The problem (1) and (13) with the initial condition (2), admits a unique optimal solution ![]() associated with an optimal control
associated with an optimal control ![]() on
on![]() , with a fixed final time
, with a fixed final time![]() . Moreover, there are adjoint functions
. Moreover, there are adjoint functions ![]() satisfying
satisfying
![]() (14)
(14)
and the transversality conditions ![]() Furthermore,
Furthermore,
![]() (15)
(15)
Proof. The existence of optimal solution ![]() associated with the optimal control
associated with the optimal control ![]() is from the convexity of integrand of cost function (13) with respect to the control p and Lipschitz property of state model with respect to the state variables
is from the convexity of integrand of cost function (13) with respect to the control p and Lipschitz property of state model with respect to the state variables ![]() (for more details, see [11] [12] ). According to the Pontryagin maximum principle [13] , if
(for more details, see [11] [12] ). According to the Pontryagin maximum principle [13] , if ![]() is optimal for the problem considered, then there is a nontrivial absolutely continuous mapping
is optimal for the problem considered, then there is a nontrivial absolutely continuous mapping ![]() ,
, ![]() , called the adjoint vector, such that
, called the adjoint vector, such that
![]()
and
![]() (16)
(16)
where the Hamiltonian H is defined by
![]()
Together with the minimality condition
![]() (17)
(17)
Satisfied almost everywhere on![]() . Moreover, the transversality conditions
. Moreover, the transversality conditions ![]() hold,
hold,![]() . System (14) is derived from (16), and the optimal control (15) comes from minimality condition (17).
. System (14) is derived from (16), and the optimal control (15) comes from minimality condition (17).
5. Numerical Simulation
Now, some numerical simulations are performed to illustrate the main theoretical results above for stability of equilibria using the Runge-Kutta method in the software MATLAB. The values of parameters for model (1) are listed in Table 1, fixing the values of model parameters as follows:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . For such choice of parameters,
. For such choice of parameters, ![]() ,
,![]() .
.
In Figure 2(a) and Figure 2(b), setting the values of other parameters except above are:![]() ,
, ![]() ,
, ![]() , so it is easy to obtain that
, so it is easy to obtain that![]() . Noticing that infectious individuals are decreasing to zero eventually and the total number of mosquitoes are decreasing to zero from Figure 2(a) and Figure 2(b). Obviously, for different initial values, this is identified to the theoretical conclusion of Theorem 2.
. Noticing that infectious individuals are decreasing to zero eventually and the total number of mosquitoes are decreasing to zero from Figure 2(a) and Figure 2(b). Obviously, for different initial values, this is identified to the theoretical conclusion of Theorem 2.
To illustrate the asymptotic behaviors of infectious classes (individuals and mosquitoes) and susceptible mosquitoes when the parameter conditions satisfying Theorem 3, set![]() ,
, ![]() ,
, ![]() , other parameters are fixed as above. Here,
, other parameters are fixed as above. Here, ![]() and
and ![]() are obtained. Seeing that infectious individuals and mosquitoes are
are obtained. Seeing that infectious individuals and mosquitoes are
decreasing to zero eventually, whereas the number of susceptible mosquitoes are not decreasing to zero but having a positive stable state from Figure 3(a) and Figure 3(b). Obviously, for different initial values in figures, this also tests and verifies the theoretical results of Theorem 3.
In order to further investigate the dynamic behavior of model (1), setting![]() ,
,![]() ,
, ![]() and other parameters are fixed as above. Here,
and other parameters are fixed as above. Here, ![]() and
and ![]() are obtained. It is easy to see that susceptible and infectious mosquitoes
are obtained. It is easy to see that susceptible and infectious mosquitoes
are both having positive stable states (see Figure 4(b)). As for the numbers of infectious individuals, although the numbers are not too many, there is a positive stable state in Figure 4(a) if the figure is amplified. That is to say, the existence of positive equilibrium are confirmed and the positive equilibrium is likely to locally asymptotically stable for ![]() and
and![]() . Of course, this conclusion also needs further confirm, don’t make discussion in this paper.
. Of course, this conclusion also needs further confirm, don’t make discussion in this paper.
To better visualize the impact of maturation delay of![]() , fixing
, fixing![]() ,
, ![]() and other parameters are fixed as above. Obviously, from Figure 5(a) seeing that in
and other parameters are fixed as above. Obviously, from Figure 5(a) seeing that in
pace with increasing of the value of![]() , the number of mosquitoes are decreasing, that is to say, the bigger the value of
, the number of mosquitoes are decreasing, that is to say, the bigger the value of![]() , the few the number of mosquitoes; the bigger the value of
, the few the number of mosquitoes; the bigger the value of![]() , the better the effect of controlling the virus of dengue. To study the effects of the vertical transmission rate q, make
, the better the effect of controlling the virus of dengue. To study the effects of the vertical transmission rate q, make![]() ,
, ![]() and other parameters are fixed as above (Figure 5(b)). Obviously, for a bigger value q, the only peak of explosion of
and other parameters are fixed as above (Figure 5(b)). Obviously, for a bigger value q, the only peak of explosion of ![]() or
or ![]() is bigger, that is, the number of infectious individuals or mosquitoes are
is bigger, that is, the number of infectious individuals or mosquitoes are
increasing with the value q.
Fund
This work was supported in part by the Natural Science Foundation of Xinjiang (Grant No. 2016D01C046).