The Z-Valued Characters for the Huge Symmetry of Hexamethylethane ()
1. Introduction
An object is called symmetrical if some movement or operation leaves the object in a position indistinguishable from its original position. The symmetry of molecules and solids is a very powerful tool for developing and understanding bonding and physical properties used to predict the nature of molecular orbitals. Chemists and physicists classify molecules in terms of their symmetry. It is of some value to recognize that all molecules that have the same basic “structure” share a number of common properties. The process of doing the rotation, reflection etc. is referred to as a symmetry operation if it does not change the appearance of the molecule. It is easy to see that all symmetry operations of a molecule form a group named symmetry group of molecule under consideration [1] - [20] . A molecule is said to be non-rigid if there are several local minima on the potential energy surface easily surmountable by the molecular system via a tunneling rearrangement. A non-rigid molecule typically possesses several potential valleys separated by relatively low energy barriers, and thus exhibits large amplitude tunneling dynamics among various potential minima. Because of this deformability, the non-rigid molecules exhibit some interesting properties of intramolecular dynamics, spectroscopy, dynamic NMR and so on, all of which can be interpreted by resorting to group theory. Group theory is the best formal method to describe the symmetry concept of molecular structures. Group theory has numerous applications to large amplitude vibrational spectroscopy or small organic molecules, in particular.
Character tables for reducing linear representations into irreducible ones belong to the standard repertoire of chemical group theory. Since they are widely applied to various fields of chemistry, textbooks on chemical group theory use many pages to introduce the concept and applications of character tables. On the other hand, the concept of mark tables for assigning permutation representations to coset representations, which has been developed by Burnside, has been unjustly neglected for a long time not only in chemical fields but also in mathematics. Among several works using mark tables, Kerber’s contribution, Redfield’s research can be mentioned for discussing mathematical applications. In order to develop new methods of combinatorial enumeration of isomers, some relationships between character tables containing characters for irreducible representations and mark tables containing marks for coset representations have been clarified by Shinsaku Fujita who proposed not only markaracter tables, which enable us to discuss characters and marks on a common basis, but Q-Conjugacy character tables, which are obtained for finite groups [2] - [11] [20] .
The present study investigates all the dominant subgroups and the integer-valued characters of the symmetry of Hexamethylethane (Figure 1) with the aid of GAP system [21] .
![]()
Figure 1. The structure of hexamethylethane.
2. Results and Discussion
In this section we first describe some notation which will be kept throughout.
Let G be an arbitrary finite group and h1, h2 Î G. We say h1 and h2 are Q-conjugate if there exists t Î G such that t−1
1> t =
2>. This is an equivalence relation on the group G and generates equivalence classes that are called dominant classes. Therefore G is partitioned into dominant classes.
Suppose that H is a cyclic subgroup of order n of a finite group G and K is a conjugacy class of G. Then, the maturity discriminant of H denoted by m(H) is an integer delineated by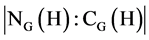
. In addition, the dominant class of K Ç H in the norma-
lizer 
is the union of t =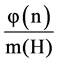 
conjugacy classes of G where φ is the Euler
function, i.e. the maturity of G is clearly defined by examining how a dominant class corresponding to H contains conjugacy classes. The group G should be a matured group if t = 1, but if t ≥ 2, the group G is unmatured concerning subgroup H, see [4] - [9] .
Let Cu×u be a matrix of the character table for an arbitrary finite group G. Then, C is transformed into a more concise form called the Q-Conjugacy character table denoted by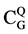 
containing integer-valued characters. By Theorem 4 in [5] , the dimension of a Q-conjugacy character table is equal to its corresponding markaracter table, i.e. 
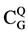is an m × m-matrix where m is the number of dominant classes or the number of non- conjugate cyclic subgroups denoted by SCSG, see [9] .
Assume that N be a normal subgroup of G and H is another subgroup of G such that H Ç N = {e} and G = HN = {xy| x Î H, y Î N}, then we say that G is a semidirect product of N by H denoted by N ⋉ H. Let us make some observations about semidirect product. Since G = NH, each x Î G can be written uniquely as x = nh for some n Î N and h Î H. Fix element h in H, since N is normal in G, conjugation by h maps N to H, consequently we can define a map ϕh: N → N by ϕh(n) = hnh−1 for n Î N. It is easy to show that ϕh is an automorphism of N and also that ϕhoϕj = ϕhj for any j Î H. Therefore, we have constructed a homomorphism ϕ: H → Aut(N), where ϕ(h) = ϕh, we call ϕ conjugation homomorphism of the semidirect product G and write G = N ⋉ ϕ H. We can see that if the homomorphism ϕ: H → Aut(N) defined above is trivial, then semidirect product reduces to the direct product of N × H. It is a well-known fact that the homomorphism ϕ completely determines the semi-direct product.
The full non-rigid group of hexamethylethane is the semi-direct product of the direct products of six copies of the cyclic group Z3 by D6 (the dihedral group of order 12), i.e. (Z3 × Z3 × Z3 × Z3 × Z3 × Z3) ⋉ D6 of order 8748, see for further details in [18] .
The first author shows that the semi-direct product of the matured groups again is a matured group, but the semi-direct product is unmatured if at least one of the groups is unmatured, see [19] .
Now consider the full non-rigid group of hexamethylethane i.e. HEX = (Z3 × Z3 × Z3 × Z3 × Z3 × Z3) ⋉ D6 then, HEX is an unmatured group [19] , see Figure 1.
We will use for an arbitrary conjugacy class of G of elements of order n the notation
![]()
![]()
![]()
Table 1. The corresponding non-redundant set of cyclic subgroups of HEX.
nX, where X = a, b, c, ∙∙∙
Referring to the reported GAP program [21] - [28] , we are able to introduce all the dominant classes (i.e. Ki) as follow:
K1 = 1a, K2 = 3a È 3b, K3 = 3c È 3e, K4 = 3d, K5 = 3f È 3l, K6 = 3g È 3n, K7 = 3h È 3m, K8 = 3i, K9 = 3j È 3k, K10 = 3o È 3ad, K11 = 3p È 3af, K12 = 3q È 3ae, K13 = 3r È 3ai, K14 = 3s È 3ah, K15 = 3t È 3ag, K16 = 3u, K17 = 3v È 3aa, K18 = 3w È 3x, K19 = 3y È 3ac, K20 = 3z, K21 = 3ab, K22 = 3aj È 3bq, K23 = 3ak È 3ay, K24 = 3al È 3bs, K25 = 3am È 3bj, K26 = 3an È 3br, K27 = 3ao È 3bc, K28 = 3ap È 3bx, K29 = 3aq È 3bz, K30 = 3ar È 3by, K31 = 3at È 3bw, K32 = 3au È 3bv, K33 = 3av, K34 = 3aw È 3bu, K35 = 3ax È 3bt, K36 = 3az È 3bi, K37 = 3ba È 3bb, K38 = 3bd È 3bp, K39 = 3be È 3bo, K40 = 3bf, K41 = 3bg È 3bh, K42 = 3bk, K43 = 3bl È 3bm, K44 = 3n È 3as, K45 = 3ca È 3cm, K46 = 3cb È 3cl, K47 = 3cc È 3ch, K48 = 3cd È 3cj, K49 = 3ce, K50 = 3cf È 3ck, K51 = 3cg, K52 = 3ci, K53 = 3cn, K54 = 9a È 9b, K55 = 9c È 9e, K56 = 9d, K57 = 6a, K58 = 18a È 18b, K59 = 2a, K60 = 6b È 6c, K61 = 6d È 6f, K62 = 6e, K63 = 6g È 6j, K64 = 6h È 6i, K65 = 2b, K66 = 6k È 6l, K67 = 6m È 6p, K68 = 6n È 6r, K69 = 6o È 6q, K70 = 6s
6ab, K71 = 6t È 6aa, K72 = 6u È 6ea, K73 = 6v È 6ag, K74 = 6w È 6af, K75 = 6x, K76 = 6y
6ad, K77 = 6z È 6ac, K78 = 6ah È 6aw, K79 = 6ai, K80 = 6aj È 6ay, K81 = 6ak
6as, K82 = 6al È 6ax, K83 = 6am È 6an, K84 = 6ao È 6bb, K85 = 6ap È 6av, K86 = 6aq È 6ba, K87 = 6ar, K88 = 6at, K89 = 6au È 6az, K90 = 2c, K91 = 6bc È 6bd, K92 = 6be È 6bh, K93 = 6bf È 6bj, K94 = 6bg È 6bi, K95 = 6bk È 6bq, K96 = 6bl, K97 = 6bm È 6bs, K98 = 6bn È 6bp and K99 = 6bo È 6br. Their corresponding non-redundant set of cyclic subgroups of HEX (i.e. Gi) are sorted in Table 1.
Assume Cbe the character table of HEX = <(1, 2, 3, 4, 5, 6), (2, 6)(3, 5), (7, 8, 9), (10, 11, 12), (13, 14, 15), (16, 17, 18), (19, 20, 21), (22, 23, 24)> i.e. group HEX is generated by generators (1, 2, 3, 4, 5, 6), (2, 6)(3, 5), (7, 8, 9), (10, 11, 12), (13, 14, 15), (16, 17, 18),
(19, 20, 21) and (22, 23, 24), which is a 174 × 174 matrix, contains 174 irreducible characters, see [18] . Now by considering the above outputs, we calculate all the integer-valued characters by the row-reductions (respectively, column-reductions) of HEX as a 99 × 99-matrix which are stored as in Table 2, see [27] [28] for more details.
Besides, the Q-conjugacy character table of the symmetry of a given molecule would also be valuable in other applications such as in the context of chemical applications of graph theory and aromatic compounds, see [1] - [6] [23] - [28] .
Acknowledgements
The authors are indebted to the referees for useful discussion and suggestions.