The Effect of State-Dependent Control for an SIRS Epidemic Model with Varying Total Population

Fuwei Zhang, Linfei Nie^*

College of Mathematics and Systems Science, Xinjiang University, Urumqi, China.

DOI: 10.4236/jamp.2016.410191                

Abstract

Based on the mechanism of prevention and control of infectious disease, we propose, in this paper, an SIRS epidemic model with varying total population size and state-dependent control, where the fraction of susceptible individuals in population is as the detection threshold value. By the Poincaré map, theory of differential inequalities and differential equation geometry, the existence and orbital stability of the disease-free periodic solution are discussed. Theoretical results show that by state-dependent pulse vaccination we can make the proportion of infected individuals tend to zero, and control the transmission of disease in population.

Keywords

SIRS Epidemic Model, Varying Total Population, State-Dependent Pulse Control, Periodic Solution, Orbital Stability

1. Introduction

It is generally known that the spread of infectious diseases has been a threat to healthy of human beings and other species. In order to prevent and control the transmission of disease (such as hepatitis C, malaria, influenza), pulse vaccination as an effective strategy has been widely studied by many scholars in the study of mathematical epidemiology. In the classical research literature it is usually assumed that the pulse vaccination occurs at fixed moment intervals and total population size remains constant [1] [2] , and so on. Although fixed time pulse vaccination strategy is better than the traditional vaccination strategies (continuous vaccination), it has a few disadvantages. For these reasons, a new vaccination strategies, state-dependent pulse vaccination is proposed when the number of the susceptible individuals or infected individuals reaches a critical value. Clearly, the latter control strategies are more ra- tional for disease control because of its efficiency, economy, and feasibility. In recent years, mathematical models with state-dependent pulse control strategies have been extensively applied to research fields of applied science, such as pest management model [3] , tumor model [4] , predator-prey model [5] , and others. Particularly, Nie et al. [6] investigated an SIR epidemic model with state-dependent pulse vaccination. In it, authors obtained the existence and stability of positive order-1 and order-2 periodic solution. Tang et al. [7] proposed an SIR epidemic model with state-dependent pulse control strategies. Authors demonstrated that the combination of pulse vaccination and treatment is optimal in terms of cost under certain conditions, and studied the existence and stability of periodic solution.

As far as we know, epidemic model with varying total population and state-de- pendent feedback control strategies had never been done in the literatures. Hence, in this paper, the dynamical behavior of an SIRS epidemic model with varying total population and state-dependent pulse control strategy is studied. The main aim is to explore how the state-dependent pulse control strategy affects the transmission of diseases. The remaining part of this paper is organized as follows. In the next section, an SIRS control model is constructed and some preliminaries are introduced, which are useful for the latter discussion. In section 3, we will focus our attention on the existence and orbital stability of disease-free periodic. Finally, some concluding remarks are presented in the last section.

2. Models and Preliminaries

In the study of the dynamic properties of infectious diseases, it was found that when the popularity of disease for a long time total population size change this factor should be considered. In this case, Busenberg et al. [12] proposed the following SIRS epidemic model with varying total population size.

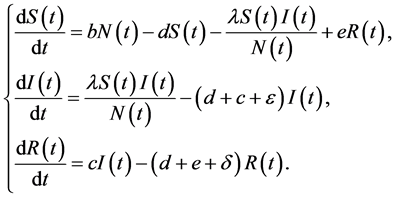(1)

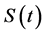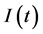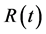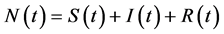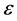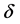Here, , and denote the numbers of susceptible, infected, and recovered individuals respectively, and denote the total population size at time t. The parameters in the model have the following features: b is the per capita birth rate with the assumption that all newborns are susceptible; d is the per capita disease free death rate of the population; the constants and denote the excess per capita death rate of infected individuals and recovered individuals, respectively; c is the per capital recovery rate of the infected individuals and e is the per capita loss of immunity rate for recovered individuals. It is assumed that all susceptible group becomes infected at a rate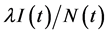, where 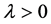is the effective per capita contract rate of infective individuals. All parameter values are assumed to be non- negative and.

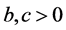Since the susceptible individuals are immunity toward certain infectious diseases in the crowd, once infected individuals get into the susceptible groups, this will lead to the outbreak of the diseases. For this reason, we propose a pulse vaccination function as follows 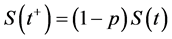where p 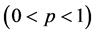is the proportion by which the susceptible individuals numbers is reduced by pulse vaccination.

Taking into account pulse vaccination as state-dependent feedback control strategies, model (1) can be extend to the following state-dependent pulse differential equation.

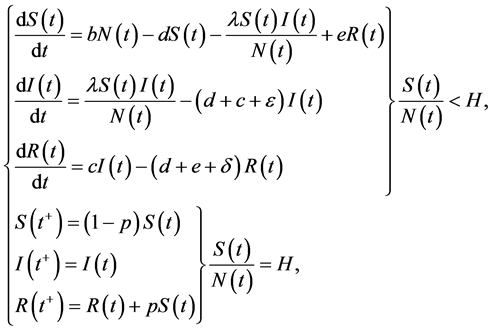(2)

where the critical threshold 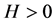is a constant. The meaning of model (2) as following: once the fraction of the susceptible individuals in the population reaches the critical value H at time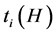, vaccination control strategies are carried out which lead to the number of susceptible and recovered individuals abruptly turn to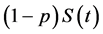, and 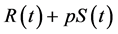respectively.

The equation for the total population size 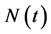can be determined from model (2)

It means that total population size is not constant. In such situations, to discuss the dynamics behavior of model (2) we need to consider the fraction of indivi- duals in the three epidemiological classes, namely

(3)

It following from (3) that we can transforms model (2) into the following model for these new variables

(4)

Define three threshold parameter as follows

On the dynamics of model (4) without pulse effect has been studied in [12] . Relevant conclusions can be summarized as the following Theorem 1.

Theorem 1. For model (4) without pulse control, the following result hold true.

1) The disease-free equilibrium always exists and is globally asymptoti- cally stable in the feasibility region when- ever, and unable when.

2) When, there exist a unique endemic equilibrium, which is globally asymptotically stable in the feasibility region where

and can be found by solving equation

3) The total population has the asymptotic behavior if

, and if.

4) When, the total infected population has the asymptotic behavior

if, and if.

Based on the above discussions, we just need to discuss cases (a) and (b) in Table 1.

Considering the similarities of cases (a) and (b), throughout of this paper, we discuss only the case (a). That is, in a increasing population, the number of infected individuals is converges to infinity, while the fraction of infected individuals in population is tending to a nonzero constant.

Due to, for model (4) we can eliminate by

and consider the two-dimensional model.

(5)

By the biological background, we only focus on model (5) in the biological meaning region. Besides, the globally exis- tence and uniqueness properties of solution of model (5) are guaranteed by the smoo- thness of f, which is the mapping defined by right-side of model (5), for details see [13] .

Let be an arbitrary nonempty set and be an arbitrary point. The distance between and is defined by. Set

be a solution of model (5) starting from initial point at. We define the positive orbit as follows

Firstly, on the positivity of solutions of model (5), we have the following Lemma 1.

Lemma 1. Supposing that is a solution of model (5) with the initial condition, then for all.

Proof. For any initial value, we will discuss all possible cases by the relation of the solution to the line as follows.

1) The solution intersects with line finitely many times.

For this case, due to the endemic equilibrium is globally asymptotically

Table 1. Threshold criteria and asymptotic behavior.

stable, then, for all.

2) The solution intersects with line infinitely many times.

For second situation, assume that solution intersects with line at times and. If the conclusion of Lemma 1 is false, we obtain that there exists a positive integer n and a such that

and for. The first possibility is that and. For this case, it follows from the first and third equation of model (5) that

which contradicts the fact that.

The other case is that and. In this regard, it follows from the second and fourth equation of model (5) that

which lead to a contradiction with. Therefore, according to above discussion, we can obtain that and for all. This proof is complete.

In order to address the dynamical behaviors of model (5), we could construct two sections to the vector field of model (5) by

and

Choosing section as a Poincaré section. Assume that for any point

, the trajectory starting from the initial point in- tersects section infinitely many times. That is, trajectory jumps to section at point due to pulse effect. Moreover, trajectory

will reach at section at point, and then jumps to point on section. Repeating this procedure, we get two pulse point sequences and , where is only determined by, , and. Therefore, we can define a Poincaré map of section as

(6)

From the definition of Poincaré map, it easy to get that

Obviously, function is continuously differential according to the Cauchy- Lipschitz theorem. If there exist positive integer k such that, then trajectory of model (5) is said to be order-k periodic solution.

3. Main Results

Our main purpose in this section is to investigate the existence and orbital stability of periodic solution of model (5). From the geometrical construction of phase space of model (5), we note that the trajectory from any initial point intersects section infinite times with. However, if, then trajectory from any initial point may be free from pulse effects or intersects section infinitely times, which depend on the initial con- ditions. Consequently, based on different positions of section we need to discuss the existence and orbital stability of periodic solution of model (5) in the cases of and.

Case I: The case of.

For this case, it will prove that model (5) possesses a disease-free periodic solution, which is orbitally asymptotically stable.

Suppose for all, then model (5) degenerates into the following model

(7)

Integrating the first equation of model (7) with the initial condition

, one yields

where

Assume that and, then we obtain

Therefore, model (5) possesses the following disease-free periodic solution, denoted by

(8)

where,.

On the stability of this disease-free periodic solution we have the following result.

Theorem 2. For any and the disease-free periodic solution (8) of model (5) is orbitally asymptotically stable.

Proof. We assume that section intersects line and x axis at points P and Q, respectively. From the geometrical structure of phase space of model (5), we know that trajectory starts from any point on set

will enter set. Further, set

is mapped to set

by Poincaré map (6), where. Then, set is mapped to set and

. Repeat above-mentioned procedure, we gain one point sequences and which satisfy

and

(9)

where.

From (9), it is concluded that the point sequence is monotonically decrease in the interval and converge to a fixed point in this bound region. That is.

Suppose that is a solution of small-amplitude perturbation of disease- free periodic solution with initial value, which first intersects section at point and then jumps to point

. Further, solution insects section at point again. Repeating the above process, we have two point sequences and, where. Furthermore, by, it is clear that. This shows that the disease-free periodic solution (8) of model (5) is orbitally asymptotically stable. This proof is complete.

Case II: The case of.

For this case, we know that there a point such that tra- jectory is tangent to section at the point

. Then the point is jump to the po- int on section after pulse effect. According to the different positions of point we has the following results.

Theorem 3. For any and, if

, then model (5) exists a positive order-1 periodic solution. Further, if

then model (5) exists a disease-free periodic solution (8), which is orbitally asympto- tically stable.

For this case, (8) is a disease-free periodic solution of model (5), and the proof of stability is similar to the proof of Theorem 2, we therefore omit here.

4. Concluding Remarks

In order to explore the effects of the state-dependent pulse control strategies on the transmission of the infectious diseases in a population of varying size, an SIRS epidemic model with varying total population and state-dependent pulse control strategy is proposed and analyzed in this paper. Theoretically analyzing this control model, we find that a disease-free periodic solution always exists and orbitally stable when condition holds. Theoretical results shows that the disease finally disappears if we control the fraction of susceptible individuals in relatively low levels. Furthermore, we obtained some sufficient condition on existence and stability of the positive order-1 periodic solution when. This amounts to that we can control the fraction of susceptible individuals and infected individuals within a retain range for a long time by appropriately choose the immune strength p and critical threshold H. Therefore, we can concluded that state-dependent pulse vaccination is a feasible, eco- nomic, and high efficient method to prevention and control spread of diseases.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Fund

This research has been partially supported by the Natural Science Foundation of Xinjiang (Grant no. 2016D01C046).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Hu, Z., Ma, W. and Ruan, S. (2012) Analysis of SIR Epidemic Models with Nonlinear Incidence Rate and Treatment. Mathematical Biosciences, 238, 12-20. http://dx.doi.org/10.1016/j.mbs.2012.03.010
[2]	Meng, X. and Chen, L. (2008) The Dynamics of a New SIR Epidemic Model Concerning Pulse Vaccination Strategy. Applied Mathematics and Computation, 197, 582-597. http://dx.doi.org/10.1016/j.amc.2007.07.083
[3]	Zhang, T., Meng, X., Liu, R. and Zhang, T. (2014) Periodic Solution of a Pest Management Gompertz Model with Impulsive State Feedback Control. Nonlinear Dynamics, 78, 921-938. http://dx.doi.org/10.1007/s11071-014-1486-y
[4]	Tang, B., Xiao, Y., Tang, S. and Cheke, R. (2016) A Feedback Control Model of Comprehensive Therapy for Treating Immunogenic Tumours. International Journal of Bifurcation and Chaos, 26, 22 p.
[5]	Tang, S., Tang, B., Wang, A. and Xiao, Y. (2015) Holling II Predator-Prey Impulsive Semi-Dynamic Model with Complex Poincaré Map. Nonlinear Dynamics, 81, 1575-1596. http://dx.doi.org/10.1007/s11071-015-2092-3
[6]	Nie, L., Teng, Z. and Toores, A. (2012) Dynamics Analysis of an SIR Epidemic Model with State Dependent Pulse Vaccination. Nonlinear Analysis: Real World Applications, 13, 1621-1629. http://dx.doi.org/10.1016/j.nonrwa.2011.11.019
[7]	Tang, S., Xiao, Y. and Clancy, D. (2005) New Modelling Approach Concerning Integrated Disease Control and Cost-Effectivity. Nonlinear Analysis: Theory, Methods and Applications, 63, 439-471. http://dx.doi.org/10.1016/j.na.2005.05.029
[8]	Yang, W., Sun, C. and Arino, J. (2010) Global Analysis for a General Epidemiological Model with Vaccination and Varying Population. Journal of Mathematical Analysis and Applications, 372, 208-223. http://dx.doi.org/10.1016/j.jmaa.2010.07.017
[9]	Hui, J. and Zhu, D. (2007) Dynamics of SEIS Epidemic Models with Varying Population Size. International Journal of Bifurcation and Chaos, 15, 1513-1529. http://dx.doi.org/10.1142/S0218127407017902
[10]	Li, J. and Ma, Z. (2002) Qualitative Analyses of SIS Epidemic Model with Vaccination and Varying Total Population Size. Mathematical and Computer Modelling, 35, 1235-1243. http://dx.doi.org/10.1016/S0895-7177(02)00082-1
[11]	Naresh, R. and Tripathi, A. (2005) Modelling and Analysis of HIV-TB Co-Infection in a Variable Size Population. Mathematical Modelling and Analysis, 10, 275-286.
[12]	Busenberg, S. and van den Driessche, P. (1990) Analy-sis of a Disease Transmission Model in a Population with Varying Size. Journal of Mathematical Biology, 28, 257-270. http://dx.doi.org/10.1007/BF00178776
[13]	Lakshmikantham, V., Bainov, D. and Simeonov, P. (1989) Theory of Impulsive Differential Equations. World Scientific, Singapore. http://dx.doi.org/10.1142/0906