A Remark on Polynomial Mappings from Cⁿ to C^n-1 and an Application of the Software Maple in Research

Thi Bich Thuy Nguyen

UNESP, Universidade Estadual Paulista, “Júlio de Mesquita Filho”, São José do Rio Preto, Brasil.

DOI: 10.4236/am.2016.715154                

Abstract

In [1], we construct singular varieties associated to a polynomial mapping where such that if G is a local submersion but is not a fibration, then the 2-dimensional homology and intersection homology (with total perversity) of the variety are not trivial. In [2], the authors prove that if there exists a so-called very good projection with respect to the regular value of a polynomial mapping , then this value is an atypical value of G if and only if the Euler characteristic of the fibers is not constant. This paper provides relations of the results obtained in the articles [1] and [2]. Moreover, we provide some examples to illustrate these relations, using the software Maple to complete the calculations of the examples. We provide some discussions on these relations. This paper is an example for graduate students to apply a software that they study in the graduate program in advanced researches.

Keywords

Singularities, Intersection Homology, Polynomial Mappings, Bifurcation

1. Preliminaries

1.1. Intersection Homology

We briefly recall the definition of intersection homology; for details, we refer to the fundamental work of M. Goresky and R. MacPherson [3] (see also [4] ).

Definition 1.1. Let X be an m-dimensional variety. A stratification of X is the data of a finite filtration

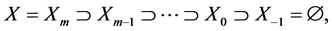
such that for every i, the set 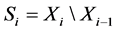is either an empty set or a manifold of dimension i. A connected component of 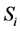is called a stratum of X.

We denote by, the open cone on the space L, the cone on the empty set being a point. Observe that if L is a stratified set then 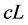is stratified by the cones over the strata of L and an additional 0-dimensional stratum (the vertex of the cone).

Definition 1.2. A stratification of X is said to be locally topologically trivial if for every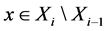, , 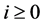there is an open neighborhood 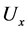of x in X, a stratified set L and a homeomorphism

such that h maps the strata of 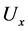(induced stratification) onto the strata of (product stratification).

The definition of perversities has originally been given by Goresky and MacPherson:

Definition 1.3. A perversity is an -uple of integers such that and, for.

Traditionally we denote the zero perversity by, the maximal perversity by, and the middle perversities by

(lower middle) and (upper middle). We say that the perversities and are complementary if.

Let X be a variety such that X admits a locally topologically trivial stratification. We say that an i-dimensional subset is -allowable if

Define to be the -vector subspace of consisting in the chains such that is -allowable and is -allowable.

Definition 1.4. The intersection homology group with perversity, denoted by, is the homology group of the chain complex.

The notation will refer to the intersection homology with compact supports, and the notation will refer to the intersection homology with closed supports. In the compact case, they coincide and will be denoted by. In general, when we write (resp.,), we mean the homology (resp., the intersection homology) with both compact supports and closed supports.

Goresky and MacPherson proved that the intersection homology is independent on the choice of the stratification satisfying the locally topologically trivial conditions.

The Poincaré duality holds for the intersection homology of a (singular) variety:

Theorem 1.5. (Goresky, MacPherson [3] ) For any orientable compact stratified semi-algebraic m-dimensional variety X, the generalized Poincaré duality holds:

where and are complementary perversities.

For the non-compact case, we have:

1.2. The Bifurcation Set, the Set of Asymptotic Critical Values and the Asymptotic Set

Let where be a polynomial mapping.

i) The bifurcation set of G, denoted by is the smallest set in such that G is not -fibration on this set (see, for example, [5] ).

ii) When, we denote by the set of points at which the mapping G is not proper, i.e.

and call it the asymptotic variety (see [6] ). The following holds: ( [6] ).

2. Varieties Associated to a Polynomial Mapping

In [1] , we construct singular varieties associated to a polynomial mapping as follows: let such that, where is the set of critical values of G. Let be a real function such that

where, and. Let us denote and consider as a real mapping from to. Let us define

where is the (real) Jacobian matrix of at x. Notice that, so we have.

Proposition 2.1. [1] For an open and dense set of polynomial mappings such that, the variety is a smooth manifold of dimension.

Now, let us consider:

a) the restriction of G on,

b).

Since the dimension of is (Proposition 2.1), then locally, in a neighbourhood of any point in, we get a mapping. Then there exists a covering of by open semi-algebraic subsets (in) such that on every element of this covering, the mapping F induces a diffeomorphism onto its image (see Lemma 2.1 of [7] ). We can find semi-algebraic closed subsets (in) which cover as well. Thanks to Mostowski’s Separation Lemma (see Separation Lemma in [7] , p. 246), for each, there exists a Nash function, such that is positive on and negative on. We can choose the Nash functions such that tends to zero when tends to infinity. Let the Nash functions and be such that tends to zero and tends to infinity when tends to infinity. Define a variety associated to as

that means is the closure of by.

In order to understand better the construction of the variety, see the example 4.13 in [1] .

Proposition 2.2. [1] Let be a polynomial mapping such that and let be a real function such that

where, and for Then, there exists a real algebraic variety in, where, such that:

1) The real dimension of is,

2) The singular set at infinity of the variety is contained in where

3. The Bifurcation Set and the Homology, Intersection Homology of Varieties Associated to a Polynomial Mapping

We have the two following theorems dealing with the homology and intersection homology of the variety.

Theorem 3.1. [1] Let be a polynomial mapping such that. If then

1)

2) where is the total perversity.

Theorem 3.2. [1] Let, where, be a polynomial mapping such that and, where is the leading form of, that is the homogenous part of highest degree of, for. If then

1)

2)

3) where is the total perversity.

Remark 3.3. The singular set at infinity of depends on the choice of the function, since when changes, the set also changes. However, we have alway the property (see [8] ).

Remark 3.4. The variety depends on the choice of the function and the functions, but the theorems 3.1 and 3.2 do not depend on the varieties. Form now, we denote by any variety associated to. If we refer to, that means a variety associated to for any.

4. The Bifurcation Set and the Euler Characteristic of the Fibers of a Polynomial Mapping

Let be a non-constant polynomial mapping and be a regular value of G.

Definition 4.1. [2] A linear function is said to be a very good projection with respect to the value if there exists a positive number such that for all:

i) The restriction is proper,

ii) The cardinal of does not depend on, where is a regular value of L.

Theorem 4.2. [2] Let be a regular value of G. Assume that there exists a very good projection with respect to the value. Then, is an atypical value of G if and only if the Euler characteristic of is bigger than that of the generic fiber.

Theorem 4.3. [2] Assume that the zero set, where is the leading form of, has complex dimension one. Then any generic linear mapping L is a very good projection with respect to any regular value of G.

5. Relations between [1] and [2]

Let be a polynomial mapping such that. Then any is a regular value of G. Let be a real function such that where, and for From theorems 3.1 and 4.2, we have the following corollary.

Corollary 5.1. Let be a polynomial mapping such that. Assume that there exists a very good projection with respect to. If the Euler characteristic of is bigger than that of the generic fiber, then

1) for any,

2) for any, where is the total perversity.

Proof. Let be a polynomial mapping such that. Then every point is a regular point of G. Assume that there exists a very good projection with respect to. If the Euler characteristic of is bigger than that of the generic fiber, then by the theorem 4.2, the bifurcation set is not empty. Then by the theorem 3.1, we have for any and for any, where is the total perversity. +

From theorems 3.2 and 4.2, we have the following corollary.

Corollary 5.2. Let, where, be a polynomial mapping such that and, where is the leading form of. Assume that there exists a very good projection with respect to. If the Euler characteristic of is bigger than that of the generic fiber, then

1) for any,

2), for any,

3) for any, where is the total perversity.

Proof. Let, where, be a polynomial mapping such that. Then every point is a regular point of G. Assume that there exists a very good projection with respect to. By the theorem 4.2, the bifurcation set is not empty. If, then by the theorem 3.2, we have

1) for any,

2), for any,

3) for any, where is the total perversity. +

We have also the following corollary.

Corollary 5.3. Let, where, be a polynomial mapping such that. Assume that the zero set has complex dimension one, where is the leading form of. If the Euler characteristic of is bigger than that of the generic fiber, where, then

1) for any,

2), for any,

3) for any, where is the total perversity.

Proof. At first, since the zero set has complex dimension one, then by the theorem 4.3, any generic linear mapping L is a very good projection with respect to any regular value of G. Moreover, the complex dimension of the set is the complex corank of . Then. By the corollary 5.2, we get the proof of the corollary 5.3. +

Remark 5.4. We can construct the variety, where L is a very good projection defined in 4.2 as the following: Let, where, be a polynomial mapping such that. Assume that there exists a very good projection with respect to. Then L is a linear function. Assume that. Then the variety is defined as the variety, where

with, are the modules of the complex numbers and, respectively. With this variety, all the results in the corollaries 5.1, 5.2 and 5.3 hold. Moreover, the varieties make the corollaries 5.1, 5.2 and 5.3 simpler.

Remark 5.5. In the construction of the variety [1] (see section 2), if we replace F by the restriction of to, that means

then we have the same results than in [1] . In fact, in this case, since the dimension of is, then locally, in a neighbourhood of any point in, we get a mapping. There exists also a covering of by open semi-algebraic subsets (in) such that on every element of this covering, the mapping F induces a diffeomorphism onto its image. We can find semi-algebraic closed subsets (in) which cover as well. Thanks to Mostowski’s Separation Lemma, for each, there exists a Nash function, such that is positive on and negative on. Let the Nash functions and

be such that and tend to zero where is a sequence in tending to infinity. Define a variety associated to as

We get the -dimensional singular variety in, the singular set at infinity of which is.

With this construction of the set, the corollaries 5.1, 5.2 and 5.3 also hold.

6. Some Discussions

A natural question is to know if the converses of the corollaries 5.1 and 5.2 hold. That means, let be a polynomial mapping such that then

Question 6.1. If there exists a very good projection with respect to and if either or, then is the Euler characteristic of bigger than the one of the generic fiber?

By the theorem 4.2, the above question is equivalent to the following question:

Question 6.2. If then are and?

This question is equivalent to the converse of the theorems 3.1 and 3.2. Note that by the proposition 2.2, the singular set at infinity of the variety is contained in Moreover, in the proofs of the theorems 3.1 and 3.2, we see that the characteristics of the homology and intersection homology of the variety depend on the set. In [1] , we provided an example to show that the answer to the question 6.2 is negative. In fact, let

then and if we choose the function then and; if we choose the function then and Then, we suggest the two following conjectures.

Conjecture 6.3. Does there exist a function such that if then?

Conjecture 6.4. Let be a polynomial mapping such that. Assume that there exists a very good projection with respect to. If the Euler characteristic of is constant, for any, then there exists a real positive function such that and.

Remark 6.5. The construction of the variety in [1] (see section 2) can be applied for any polynomial mapping, where, such that. In fact, if G is generic then similarly to the proposition 2.1, the variety

has the real dimension 2 m. Hence, if we consider, that means F is the restriction of G to, then locally we get a real mapping. Moreover, in this case, we also have for any (see [8] ), where

So, we can use the same arguments in [1] , and we have the following results.

Proposition 6.6. Let be a polynomial mapping, where, such that. Let be a real function such that

where, and for Then, there exists a real variety in, where, such that:

1) The real dimension of is 2 m,

2) The singular set at infinity of the variety is contained in

Similarly to [1] , we have the two following theorems (see theorems 3.1 and 3.2).

Theorem 6.7. Let, where, be a polynomial mapping such that. If then

1)

2) where is the total perversity.

Theorem 6.8. Let, where, be a polynomial mapping such that. Assume that, where is the leading form of. If then

1) for any,

2), for any,

3) for any, where is the total perversity.

7. Examples

Example 7.1. We give here an example to illustrate the calculations of the set in the case of a polynomial mapping where, and there exists a very good projection with respect to any point of. In general, the calculations of the set are enough complicate, but the software Maple may support us. That is what we do in this example.

Let us consider the Broughton’s example [9] :

We have and. In fact, since the system of equations has no solutions, then. Moreover,

and for any, we have

So is not homeomorphic to for any. Hence. We determine now all the possible very good projections of G with respect to. In fact, for any and for any, we have

Assume that is a sequence in tending to infinity. If tends to infinity then tends to zero. If tends to infinity then tends to zero. If L is a very good projection with respect to then, by definition, the restriction is proper. Then, where and. We check now the cardinal of where is a regular value of L. Let us replace

in the equation, we have the following equation

where. This equation always has three (complex) solutions. Thus, the number does not depend on. Hence, any linear function of the form, where and, is a very good projection of G with respect to. It is easy to see that the set of very good projections of G with respect to is dense in the set of linear functions.

We choose and we compute the variety associated to where. Let us denote

where. Consider G as a real polynomial mapping, we have

and

The set is the set of the solutions of the determinant of the minors of the matrix

Using Maple, we:

A) Calculate the determinants of the minors of the matrix:

1) Calculate the determinant of the minor defined by the columns 1, 2 and 3:

2) Calculate the determinant of the minor defined by the columns 1, 2 and 4:

3) Calculate the determinant of the minor defined by the columns 1, 3 and 4:

4) Calculate the determinant of the minor defined by the columns 2, 3 and 4:

B) Solve now the system of equations of the above determinants:

We conclude that where

C) In order to calculate, we have to calculate and draw, for .

1) Calculate and draw:

2) Calculate and draw:

+ Calculate and draw:

Since is the closure of then is connected and has a pure dimension, then is a cone:

Example 7.2. If we take the suspension of the Broughton’s example

then, similarly to the example 7.1, the variety is a cone as in the example 7.1 but it has dimension 4, in the space. We can check easily that the intersection homology in dimension 2 of the variety of this example is non-trivial. We get an example to illustrate the corollary 5.1.

Example 7.3. If we take the Broughton example for such that then similarly to the example 7.1, we get an example of varieties for the case where. This example illustrates the remark 6.5.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Nguyen, T.B.T. and Ruas, M.A.S. (2015) On a Singular Variety Associated to a Polynomial Mapping. ArXiv:1503.08079.
[2]	Ha, V.H. and Nguyen, T.T. (2011) On the Topology of Polynomial Mappings from Cn to Cn-1. International Journal of Mathematics, 22, 435-448. http://dx.doi.org/10.1142/S0129167X11006842
[3]	Goresky, M. and MacPherson, R. (1980) Intersection Homology Theory. Topology, 19, 135-162. http://dx.doi.org/10.1016/0040-9383(80)90003-8
[4]	Brasselet, J.-P. (2015) Introduction to Intersection Homology and Perverse Sheaves. Instituto de Matemática Pura e Aplicada, Rio de Janeiro.
[5]	Kurdyka, K., Orro, P. and Simon, S. (2000) Semialgebraic Sard Theorem for Generalized Critical Values. Journal of Differential Geometry, 56, 67-92.
[6]	Jelonek, Z. (1993) The Set of Point at Which Polynomial Map Is Not Proper. Annales Polonici Mathematici, 58, 259-266.
[7]	Mostowski, T. (1976) Some Properties of the Ring of Nash Functions. Annali della Scuola normale superiore di Pisa, 2, 245-266.
[8]	Dias, L.R.G., Ruas, M.A.S. and Tibar, M. (2012) Regularity at Infinity of Real Mappings and a Morse-Sard Theorem. Journal of Topology, 5, 323-340. http://dx.doi.org/10.1112/jtopol/jts005
[9]	Broughton, A. (1981) On the Topology of Polynomial Hypersurfaces. Proc. Sympos. Pure Math., Vol. 40, 167-178.