Investigational Validation of PV Based DCD-MLI Using Simplified SVM Algorithm Utilizing FPGA Tied with Independent Sources ()
1. Introduction
Today, photovoltaic (PV) energy has augmented interest in wide range of electrical power applications, since it is considered as a basically limitless and generally on hand energy resource with the focus on greener sources of power particularly for distant locations where utility power is engaged [1] - [4] . Many MPPT techniques have been proposed and implemented to track the MPP from the PV array [5] - [7] . Different types of multilevel inverter topologies are presented [8] . Many methods of pulse width modulation (PWM) techniques are used to control the inverter [9] . SVPWM is used to control the variable given by the control system, and identifies each switching vector as a point in complex (α, β) space. Gupta et al. [10] carried out that the multilevel ON-time calculation problem is converted to a simple two-level ON-time calculation problem. The FPGA is a sub-class of application-specific integrated circuit controllers which provides characteristics such as fast prototyping, simple hardware and software design and higher switching frequency. This is used in the control algorithm for PV inverters considered in [11] . In a PV system, proportional controller current control scheme is used to maintain the output current sinusoidal and to get high dynamic performance from the different atmospheric conditions [12] . The scheme is [13] [14] proposed for a single-phase multilevel cascaded H-bridge inverter for PV applications with fuzzy logic control (FLC) and system-on-chip approach.
The modelling, simulation and sizing of battery energy storage systems of reducing for residential electricity peak demand in the grid are explained [15] . Energy management strategies for commercial buildings are load shedding, to reduce the electricity bill using PV and storage systems [16] . An accurate and less-disturbing active anti islanding method based on phase locked loop (PLL) for single-phase grid connected inverter systems [17] . The modeling and simulation of three-phase multilevel inverter using sinusoidal pulse width modulation for grid connected photovoltaic system with fuzzy MPPT are proposed in [18] . The mathematical model for micro-source design of an intelligent building integrated with micro-grid is discussed [19] . According to the standard Std IEEE-929-2000 [20] , a lower percentage of THD indicates higher quality of an output waveform for utility interface of PV systems.
This paper describes the prototype development of PV based DCD-MLI using simplified SVM algorithm utilizing FPGA tied with independent sources. The three-level DCD-MLI model and control algorithm are developed and simulated in the SimPowerSystem block set environment. Indeed, the paper presents the operation principle and control algorithm of the PV based DCD-MLI utilizing FPGA tied with independent sources. This is essential due to the fact that it is the core in the PV-based integrated buildings, both remote and grid-connected buildings. Here, the grid tied PV-based DCMLI is effectively integrated and utilized for achieving the energy-efficiency type of buildings. Considering the significance of the aforementioned PV-based inverter, the PV source can be fully utilized and integrated in specially design buildings where the available PV energy can be easily harvested by using the proposed PV-based inverter. The proposed system consists of a grid tied PV three-phase three-level DCMLI as shown in Figure 1.
The following are the salient features of the proposed scheme.
![]()
Figure 1. General diagram of grid connected photovoltaic system.
1. The inverter is used.
a) To control DC bus voltage.
b) To convert DC input to AC output at the same waveforms as the three phase lines and
c) To ensure high quality of the injected power.
2. An intelligent control technique using FLC is associated to an MPPT control of the PV system, whose main property is to extract the maximum power from the PV generator and improve energy conversion efficiency under different environmental conditions.
3. It aims to control the active and regulate the reactive power injected in to the grid.
2. Space Vector Modulation Algorithm for DCD-MLI
2.1. SVM Algorithm
In this paper, SVM technique is proposed to generate gating signals generation to the inverter. The space vector VSP constituted by the pole voltages of DCD-MLI VR0, VY0, VB0 with phase displacement 1200 is defined as in Equation (1)
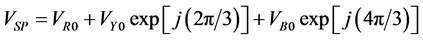 (1)
(1)
Vα0 and Vβ0 are the two rectangular components solved by the space vector VSP can be defined as the following equations.
 (2)
(2)
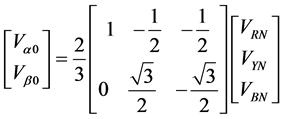 (3)
(3)
Equating the volt-seconds equation along α0 axis is defined as in Equation (4),
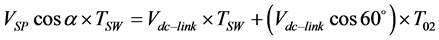 (4)
(4)
Equating the volt-seconds equation along β0 axis is defined as in Equation (5),
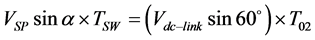 (5)
(5)
The values for the ON-time periods are T01, T02, T0 are obtained by solving the Equation (4) and (5).
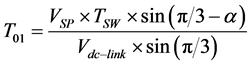 (6)
(6)
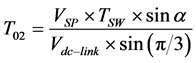 (7)
(7)
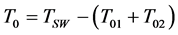 (8)
(8)
By switching amongst the DCD-MLI switching states positioned at the vertices, the reference voltage vector able to be reproduced in the average sense and contiguous closeness to it. The reference voltage in terms of volt-seconds with nearest three states are equated, the duty cycles are obtained by following equation.
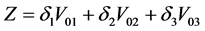 (9)
(9)
where δ1, δ2, and δ3 are duty cycles of the voltage vectors in DCD-MLI space vector diagram nearer to the reference vector and Z is the voltage reference vector.
2.2. Duty Cycle Calculation and Switching Loss Reduction
The space vector diagram represents the vector states at vertices of each region are shown in Figure 2. The sector-1 of the five-level vector diagram is shown in Figure 3.
![]()
Figure 2. Space vector diagram for three-level inverter.
![]()
Figure 3. Space vector diagram for three-level inverter for sector-1.
In three-level inverter, the reference vector Z3 is located in region-2. In four-level inverter, the reference vector Z4 is located in region-8. In five-level inverter, the reference vector Z5 is located in region-12. The reference vectors projected on to zero and 600 axes are (Z × 1) and (Z × 2), where (Z = 3 or 4 or 5). Through the sequential switching operation of nearest three switching states of inverter, the reference vector can be synthesized. The new vectors length and in each region the reference vector Z1 and Z2 are derived the following Equation (10) and Equation (11).
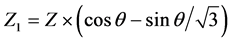 (10)
(10)
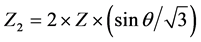 (11)
(11)
The reference voltages of each vertices of each duty cycle are Z1, Z2 and [1 − (Z1 + Z2)]. The duty cycles or ON-time for SVM switching states are V1, V2, and V3. The values of ON-times are (Z1 − 0.25), Z2 and (0.75 − Z1 − Z2). The values of Z1 and Z2 are used to identify, where reference vector is located. The ON-time period for each state of the inverter is calculated with duty cycles are represented following Equations (12)-(14)
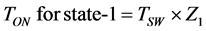 (12)
(12)
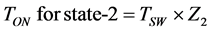 (13)
(13)
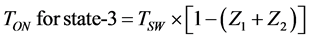 (14)
(14)
In three-level inverter, the redundant switching states cause certain voltage vectors correspond to two or three switching states. The main principle of the algorithm is that, the changing of switch states causes only the voltage (switch state) of the one phase change every time. When the rotating vector rotates from sector S14 to sector S15 the switching states will modulate as following sequence (221 → 220 → 210 → 110 → 110 → 210 → 220 → 221) → (221 → 220 → 120 → 110 → 110 → 120 → 220 → 221). When the rotating space vector VZ is in sector S14, VZ can be synthesized by space vector V21 or V9 (expressed by switching state 221 or 110), V14 (210), and V2 (220). When VZ falls in to sector S15, space vectors, V21 or V9 (221 or 110), V2 (220), and V15 (120), are selected to synthesize VZ. The switching states 221 and 110 express the same voltage vector and it is used as the starting state and ending state to complete the modulation process. There are a certain number of transitional switching states, but this will not change the overall output voltage magnitude and the duration of each output voltage vector.
2.3. FPGA Controller and Its Control Strategy
In this paper, FPGA using VHDL and coding are used to generate the SVM for the inverter circuit. To control tied independent sources with DCD-MLI ac output voltage, the digital PI controller can be employed. The inverter output voltages VR, VY and VB with FPGA controller are interfaced by using three voltage sensors for the part of voltage regulation. These voltage sensors attenuate the voltage to acclimatize the FPGA working voltages with precise voltage gains. The block diagram for FPGA implementation SVPWM control with finite state machine is shown in Figure 4.
The DCD-MLI output voltage VR, VY, VB with assumed unity power factor and ω is the output frequency are defined as following Equations (15)-(17).
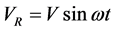 (15)
(15)
![]() (16)
(16)
![]() (17)
(17)
These voltages are scale down by using the voltage sensors and supply them to FPGA controller ADC channels for supplementary processing. For voltage regulation, these
![]()
Figure 4. Block diagram for FPGA implementation SVPWM control with finite state machine.
sampled signals are fed to voltage regulator block. These signals are sampled and fed to the voltage regulator block for voltage regulation. The PI controllers are operate efficiently, reducing the steady-state errors and regulates the output voltage using park’s transformation. The time domain of PI controller output V(t) is expressed following Equation (18)
![]() (18)
(18)
where MPRO and MINT are the gains of the proportional and integral terms, and e(t) is the error voltage. The output voltage equation of DCD-MLI is sampled based on the sampling time as expressed in Equations (15)-(17). The PI controller generates the output voltage, with minimum value error signal in every sampling time and as close as to the reference voltage. Thus, the DCD-MLI output voltage can be controlled and stabilized. This voltage regulation is made feasible by the attainment of the modulation technique and to obtain a sinusoidal ac output waveform, a SVM technique is implemented in the DCD-MLI control algorithm.
3. Simulation Model and Experimental Set-Up
Simulations are performed by using MATLAB/simulink for the proposed system. The SVM switching strategy is used in this paper. The simulation was carried out for 0.2 seconds and this involves determining the position of reference vector according to fundamental frequency f = 50 Hz, sampling frequency fs = 10 kHz and time. According to sector wherein the reference vector is, determine the switching sequence and to calculate the time for different switching states. The switching instant of a SVM pulse waveform is shown in Figure 5. The modulation index determines the shape of the output voltage of the inverter.
Figure 6 shows the results of multi DC link capacitor. It proves that the voltages are maintained constant. The overall operation is governed by the control system where the controller samples the voltages of the inverter and then generates the PWM signals for
![]()
Figure 5. Switching instant of a SVPWM pulse waveform.
![]()
Figure 6. Capacitor voltage waveform for three-level DCMLI.
driving the IGBTs. With the control scheme implementation, the inverter is able to maintain constant phase and line output voltage.
The Fuzzy MPPT tracking is shown in Figure 7. For verification of the simulated model, independent sources tied three-phase three-level DCD-MLI prototype was build, tested and evaluated in laboratory which is shown in Figure 8. The equipment used in the experimental set-up are Xilinx development tool with VHDL coding, FPGA Spartan 3A controller, digital storage oscilloscope, digital multimeter, IGBT’s, IGBT driver are used in independent sources tied three-phase three-level DCD-MLI.
4. Result and Discussion
4.1. Simulation Results
In the proposed system, the simulation result of the output line voltage of the independent sources tied three-phase three-level DCD-MLI is shown in Figure 9.
Figure 10 shows the line voltage waveform THD of the simulated inverter which is 0.35%. In this scheme, having 10 kHz for the switching frequency, these harmonic components are easily filtered out by the smaller size LC low-pass filter. The filtered ac output voltage waveforms of the three-phase independent sources tied three-level DCD-MLI are shown in Figure 11.
It can be seen that the output voltage waveforms are 50 Hz sinusoidal, balance, and displaced to each other by 120˚. Obviously the controller managed to accurately regulate the peak output phase voltage of 325 V or rms voltage of 230 V without any undesired voltage overshoots. It reveals a considerably good transient and steady-state performance of the inverter. The controller manages to precisely track the voltage reference, quickly achieve the steady-state values, and discriminates oscillation around the operating point. These results demonstrate the efficacy of the control strategy and algorithm employing the PI controller. In the three-phase system, which acquires high power capacity, the line voltage characteristics, e.g. Vab, are more significant rather than phase voltage, Van. Significantly, the rms line voltage, Vab is higher than phase voltage, Van, by a factor of √3. Therefore, theoretically, the rms line voltage of the three-phase
![]()
Figure 8. Photograph of experimental setup.
![]()
Figure 9. Output line voltage of a grid tied three-level DCMLI.
![]()
Figure 10. THD measurement of output line voltage of a grid tied three-level DCMLI.
![]()
Figure 11. Filtered three-phase output voltage waveforms of grid tied PV system.
independent sources tied three-level DCD-MLI is 440 V. The waveform of line to line voltage of independent sources tied inverter presented in Figure 12.
It can be seen, the peak level of the DCD-MLI output line voltage is approximately 622 V which is equivalent to rms voltage of 440 V. Like the phase voltage, the line voltage acquires a sinusoidal fundamental voltage of 50 Hz with a higher power capacity. According to the standard Std IEEE-929-2000 [20] , the THD of inverters output voltage and current waveforms must be less than 5%. Figure 13 shows the line voltage waveform THD of the simulated inverter which is 0.07% and complies with standard.
The frequency spectrum shows that the output waveform contains only the fundamental component with 100% in magnitude. It indicates that most of the harmonics components especially around the 10 kHz (200th harmonic order) switching frequency are filtered out from the inverter output waveforms. The current waveforms for the three- phase independent sources are shown in Figure 14. Similar to the output voltage wave- form, the phase load current waveforms exhibit a constant peak level of approximately
![]()
Figure 12. Output line voltage waveform of a grid tied PV system.
![]()
Figure 13. THD and harmonic spectrum of filtered line-to-line voltage waveform.
![]()
Figure 14. Filtered three-phase output current.
7.2 A or rms of 5.1 A. They are balanced sinusoidal waveforms of 50 Hz, and 120˚ displacement to each other. Considering the phase relation of both independent sources current and voltage waveform, they reveal in phase relationship, indicating a unity power factor feature which acquires high efficiency.
As illustrated in Figure 15, the THD of current waveform are shown. The THD of current waveform of the simulated inverter is 0.07% and in compliance with standard Std 929-2000. It can be seen that, the frequency spectrum of the independent sources current waveforms contain only the fundamental component which signifies that most of the harmonics components especially around the 10 kHz switching frequency are filtered out from the inverter output waveforms. This proves that the proposed scheme can reduce the THD which is an indispensable condition for proposed system. The low THD of both independent sources voltage and current waveform are mainly contributed by the effectiveness of the components selection of the low pass filter and the SVM switching technique implemented in the inverter control algorithm. This proves that the proposed scheme can reduce the THD which is a necessary criterion for proposed system.
4.2. Experimental Results
The experimental results are presented in order to assess the effectiveness of the proposed independent sources tied three-level DCD-MLI model and control algorithm. It also serves as a benchmark which relates the experimental achievements to the simulation and modeling concepts. VHDL code is developed to examine the switching patterns of SVM method. This code is synthesized using Xilinx ISE. The FPGA based generalized SVM is applied to control these independent sources tied DCD-MLI to track the given reference. The generation of SVM pulse waveform for three-level inverter through Xilinx. The output line voltage of the independent sources tied three-phase three-level DCD-MLI is shown in Figure 16. Figure 17 shows the line voltage waveform THD of the simulated inverter which is 1.78%.
![]()
Figure 15. FFT analysis for simulation showing the THD and harmonic spectrum of phase current Waveform.
![]()
Figure 16. Output line voltage of a grid tied three-level DCMLI.
![]()
Figure 17. THD measurement of output line voltage of a grid tied three-level DCMLI.
The inverter output phase voltage waveforms are captured and shown in Figure 18.
It is inferred that, the output voltage waveforms are stabilized at the peak voltage level of approximately 300 V which is equivalent to rms voltage of 212 V. The waveform of three-phase line voltage is presented in Figure 19.
![]()
Figure 18. Three-phase output voltage form using real PV module.
![]()
Figure 19. Output line voltage waveform of a grid tied PV system.
It is observed that, the peak level of the DCD-MLI output line voltage is approximately 600 V which is equivalent to rms voltage of 424 V. The waveforms are balanced nearly sinusoidal with a fundamental frequency of 50 Hz. The phase voltage waveform, Va, Vb and Vc are 120˚ displaced of each other as anticipated in the simulation. They exhibit some slight distortions in the waveforms which are shown by the tiny ripples and unsmooth sinusoidal waveforms. This is due to the existence of the small level of low order harmonics, e.g. 3rd, 5th and 7th harmonics, centered around the cut-off frequency of the filter which can be clearly seen in the harmonic spectrum of Figure 20. The THD of the output voltage waveforms is calculated to be 0.97% and comply with the requirement of IEEE-2000.
Finally, the three-phase independent sources current waveforms are depicted in Figure 21.
Like the voltage waveforms, current waveforms are balanced and nearly sinusoidal with the peak level of approximately 7 A or rms of 4.9 A. As anticipated, the 50 Hz sinusoidal current waveforms are 120˚ displaced to each other. Owing to the existence of the 3rd, 5th, and 7th harmonic components centered on the filter cut-off frequency, the current waveforms show slight distortions in the waveforms. As a result, the THD for the load current waveform is calculated to be 1.26% as depicted in Figure 22 which complies with the requirement of IEEE-2000.
In view of the phase relation of load current and voltage waveform, both waveforms are in-phase or unity power factor condition, which implies an efficient of power transfer. In general, the above real hardware experimental results are slightly different compared to that of simulation. Unlike simulation, the experimental results might be influenced by the uncontrollable nature of parameters, e.g. component tolerance variation and circuit parasitic inductance and capacitance which affect the performance of
![]()
Figure 20. THD of the three-phase output voltage waveform of grid tied PV system.
![]()
Figure 21. Three-phase output current waveforms.
![]()
Figure 22. THD of the three-phase output current waveforms.
the inverter especially the filter. The comparison of THD for both simulation and hardware is shown in Table 1. Nevertheless, these results presented are considered a good conformity between the experimental and simulation.
![]()
Table 1. Comparision of THD between the simulation and experimental of proposed system.
5. Conclusion
The independent sources tied three-phase DCD-MLI utilizing FPGA controller board platform is implemented. The configuration for the proposed system is designed and simulated using MATLAB/Simulink and implementation on FPGA. The simulation result gives that output voltage and current waveforms are stabilized at 1 p.u. which proves that the algorithm employing PI controllers is effective for the output regulation. This system guarantees that a fast transient response, a high disturbance rejection capability, a robust performance and lower THD are obtained. From the simulation, the THD of output voltage and current is 0.07% and 0.07%. FPGA controller with the independent sources tied three-level DCD-MLI prototype, the proposed DCD-MLI model control algorithm managed to generate the ac output power. The captured experimental results show that the inverter controller produces stable sinusoidal output voltage and current of 50 Hz which is comparable to the simulation. The proposed system is better in terms of unity power factor and less THD of output voltage and current which are 0.97% and 1.26%. As per IEEE-929-2000, low percentage of THD is obtained by both simulation and experimental. Thus, the simulation model and the prototype implementation performed well in order to show the usefulness of the conversion into the regulated ac output waveforms.