On Starlike Functions Using the Generalized Salagean Differential Operator

Saliu Afis¹, Mashood Sidiq²

¹Department of Mathematics, Gombe State University, Gombe, Nigeria.
²Department of Mathematics, University of Ilorin, Ilorin, Nigeria.

DOI: 10.4236/oalib.1102895                

Abstract

In this paper we investigate the new subclass of starlike functions in the unit disk U={z∈□:|z|＜1} via the generalized salagean differential operator. Basic proper-ties of this new subclass are also discussed.

Keywords

Salagean Differential Operator, Starlike Functions, Unit Disk, Univalent Functions, Analytic Functions and Subordination

1. Introduction

Let 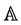denote the class of functions:

(1)

which are analytic in the unit disk. Denote by 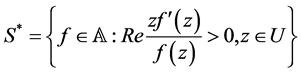the class of normalized univalent functions in U.

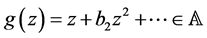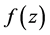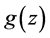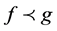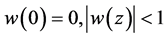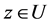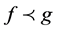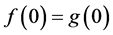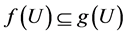Let. We say that is subordinate to (written as) if there is a function w analytic in U, with, for all. If g is univalent, then if and only if and [1] .

Definition 1 ( [2] ). Let 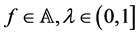and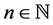. The operator 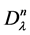is defined by

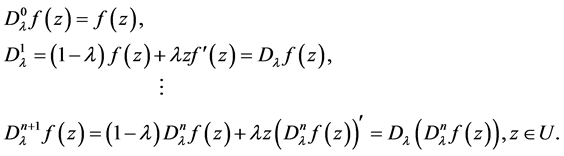(2)

Remark 1. If and, then .

Remark 2. For in (2), we obtain the Salagean differential operator.

From (2), the following relations holds:

(3)

and from which, we get

(4)

Definition 2 ( [3] ). Let, and. Then

with.

This operator is a particular case of the operator defined in [3] and it is easy to see that for any,.

Next, we define the new subclasses of.

Definition 3. A function belongs to the class if and only if

(5)

Remark 3..

Remark 4. if and only if.

Definition 4. Let, and, the set of functions satisfying:

i) is continuous in a domain of,

ii) and,

iii) when and for.

Several examples of members of the set have been mentioned in [4] [5] and ( [6] , p. 27).

2. Preliminary Lemmas

Let P denote the class of functions which are analytic in U and satisfy.

Lemma 1 ( [5] [7] ) Let with corresponding domain. If is defined as the set of functions given as which are regular in U and satisfy:

i)

ii) when.Then in U.

More general concepts were discussed in [4] - [6] .

Lemma 2 ( [8] ). Let and be complex constants and a convex univalent function in U satisfying, and. Suppose satisfies the differential subordination:

(6)

If the differential subordination:

(7)

has univalent solution in U. Then and is the best dominant in (6).

The formal solution of (6) is given as

(8)

where

and

see [9] [10] .

Lemma 3 ( [9] ). Let and be complex constants and regular in U with, then the solution of (7) given by (8) is univalent in U if (i) Re

, (ii) (iii).

3 Main Results

Theorem 1. Let and a convex univalent function in U satisfying

, and,. Let. If, then.

Proof. From (4), we have

If we suppose, we need to show that. Using the above equation and (4) and Remark 4, it suffices to show that if, then.

Now, let

Then

By (2) and (3) we have

(9)

Applying Lemma 2 with and, the proof is complete.W

Theorem 2. Let and a convex univalent function in U satisfying, and. Let. If, then

where

is the best dominant.

Proof. Let, then by Remark 4,

By (9), we have

where

To show that, by Remark 4, it suffices to show that

Now, considering the differential equation

whose solution is obtained from (8). If we proof that is univalent in U, our re-

sult follows trivially from Lemma 2. Setting and in Lemma 3, we have

i),

ii)

where, so that by logarithmic differentiation, we have

Therefore, ,

iii)

so that

Hence, is univalent in U since it satisfies all the conditions of Lemma 3. This completes the proof.W

Theorem 3..

Proof. Let. By Remark 4

From (9), let with for. Conditions (i) and (ii) of Lemma 1 are clearly satisfied by. Next, Then if. Hence, Using Remark 4, which complete the proof.W

Corollary 1. All functions in are starlike univalent in U.

Proof. The proof follows directly from Theorem 3 and Remark 4.W

Corollary 2. The class “clone” the analytic representation of convex functions.

Proof. The proof is obvious from the above corollary and Definition 4.W

The functions and are examples of functions in.

Theorem 4. The class is preserve under the Bernardi integral transformation:

(10)

Proof. let, then by Remark 4. From (10) we get

(11)

Applying on (10) and noting from Remark 1 that, we have

Let and noting that, we get

Let for. Then satisfies all the conditions of Lemma 1 and so Þ By Remark 4.W

Theorem 5. Let. Then f has integral representation:

for some.

Proof. Let. Then by Remark 4, and so for some

But, so that

Applying the operator in Definition 2, we have the result.W

With, we have the extremal function for this new subclass of which is

Theorem 6. Let. Then

The function given by (13) shows that the result is sharp.

Proof. Let, then by Remark 4,. Since it is well known that for any, , then from Remark 1 we get the result.W

Theorem 7. Let. Then

and

where

Proof. Let. Then by Theorem 6, we have

and

for.

Also, upon differentiating, we get

and

for. This complete the proof.W

Acknowledgements

The authors appreciates the immense role of Dr. K.O. Babalola (a senior lecturer at University of Ilorin, Ilorin, Nigeria) in their academic development.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Duren, P.L. (1983) Univalent Functions. Springer Verlag, New York Inc.
[2]	Al-Oboudi, F.M. (2004) On Univalent Functions Defined by a Generalized Salagean Operator. International Journal of Mathematics and Mathematical Sciences, 27, 1429-1436. http://dx.doi.org/10.1155/S0161171204108090
[3]	Faisal, I. and Darus, M. (2011) Application of a New Family of Functions on the Space of Analytic Functions. Revista Notas de Matemtica, 7, 144-151.
[4]	Babalola, K.O. and Opoola, T.O. (2006) Iterated Integral Transforms of Caratheodory Functions and Their Applications to Analytic and Univalent Functions. Tamkang Journal of Mathematics, 37, 355-366.
[5]	Miller, S.S. and Mocanu, P.T. (1978) Second Order Differential Inequalities in the Complex Plane. Journal of Mathematical Analysis and Applications, 65, 289-305. http://dx.doi.org/10.1016/0022-247X(78)90181-6
[6]	Miller, S.S. and Mocanu, P.T. (2000) Differential Subordination, Theory and Applications. Marcel Dekker, 2000.
[7]	Babalola, K.O. and Opoola, T.O. (2008) On the Coefficients of Certain Analytic and Univalent Functions. In: Dragomir, S.S. and Sofo, A., Eds., Advances in Inequalities for Series, Nova Science Publishers, 5-17. http://www.novapublishers.com
[8]	Eenigenburg, P., Miller, S.S., Mocanu, P.T. and Read, M.O. (1984) On Briot-Bouquet Differential Surbordination. Revue Roumaine de Mathématiques pures et Appliquées, 29, 567-573.
[9]	Miller, S.S. and Mocanu, P.T. (1983) Univalent Solution of Briot-Bouquet Differential Equations. Lecture Notes in Mathematics, 1013, Springer Berlin/Heidelberg, 292-310.
[10]	Srivastava, H.M. and Lashin A.Y. (1936) Some Applications of the Briot-Bouquet Differential Surbordination. Journal of Inequalities in Pure and Applied Mathematics, 37, 374-408.