On the Bump Tests of Cracked Shafts Using Acoustic Emission Techniques ()
1. Introduction
Acoustic Emission (AE) is well known as a very efficient non-destructive technique for analysis, monitoring, and diagnosis of mechanical component failures. Elastic waves associated with defects or cracks on components subjected to steady-state or varying loads can propagate through the medium and be captured by AE sensors. The great sensitivity to crack detection may be considered as one of the main advantages of AE analysis. Only in the recent years, some AE analyses have been developed for rotating machinery failure diagnosis and bearing failure detection [1] - [4] .
Reference [5] presents an experimental investigation about the influence of operating parameters on the AE levels for rotating systems supported by hydrodynamic bearings. One of their conclusions is that the viscous friction associated with the hydrodynamic bearings is one of the main sources of AE signals for rotors supported on fluid-film bearings.
Most of the recent works on the application of AE techniques in rotating systems is concerned with rotors supported by rolling bearings. Reference [6] shows that AE signals can be employed to detect failure at very early stages on rolling bearings. In their work, the AE signal level is compared with AE threshold levels associated with bearing failures. Reference [7] presents a study about the applicability of AE techniques on the detection and location of failures in ball bearings. Their experimental apparatus permits the application of very high loads on the rotating shaft in order to speed up the bearing surface degradation. They use spectral analysis on the AE time signals to evaluate and estimate efficiently the bearing crack initiation, propagation, and location.
Reference [8] devises a rotor-bearing test rig to study the AE signals associated with rolling bearing defects. The bearing defects are etched by means of electrical erosion techniques. They conclude that the AE signal amplitude varies substantially when the defect size reaches a minimum value. They also state that plastic deformation and crack growth are the main sources of AE signals in their study.
Reference [9] combines vibration analysis with AE techniques to investigate experimentally the AE signal features of rolling bearing defects. They show that there is a relationship between the AE signal amplitude and the bearing defect size, stating that the main source of AE signal in rolling bearings are the contact surface defects on the bearing races. They show that the AE technique based on two statistics, root mean square (RMS) value and kurtosis, can predict more accurately the bearing failures than the vibration techniques can.
Practically, the vast technical literature on the application of AE techniques in rotor dynamics is directed to analysis and detection of bearing failure. This paper deals with an experimental investigation about the AE analysis of cracked shafts. Six shafts with different transverse crack sizes are specially manufactured using commercial steel AISI 1020 for this work. The AE signals are captured during bump tests performed on all shafts [10] . The data acquisition system employs a wideband AE sensor (20 kHz - 1 MHz) with a sampling rate of 0.4 MHz. The AE data are evaluated by using wavelets and the AE time responses rendered from the six cracked shafts are evaluated statistically. The statistics associated with the third and fourth moments, kurtosis and skewness, are used to extract some patterns of the AE signals in time. The preliminary results indicate that the shaft discontinuity has an influence on the AE signal levels.
2. Statistical Analysis
A brief review of the statistical moments is presented to enlarge the understanding about their importance on the AE signal analysis.
2.1. Skewness
Reference [11] shows that the third-order statistical moment can be used to estimate the value of skewness of a probability distribution, which can provide an idea about the number and frequency of impulses on the AE signal distribution. Reference [12] shows that the noise associated with impact can be separated from the random noise by using the value of skewness. The skewness value is a good indicator for the signal distribution asymmetry [13] . That means that for symmetrical distributions, the skewness tend to be zero.
Skewness is a measure of the probability distribution asymmetry in relation to the average. Statistical distributions with data concentrated at one side from the mean value have large values of skewness. Negatively skewed distributions are not common in most engineering problems.
Skewness, S, can be expressed by Equation (1), in which 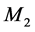 and M3 are the second and third statistical moments, respectively.
and M3 are the second and third statistical moments, respectively.
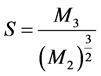 (1)
(1)
The second statistical moment  is related to the standard deviation, σ, as shown by Equation (2). The number of elements in a sample is given by n.
is related to the standard deviation, σ, as shown by Equation (2). The number of elements in a sample is given by n.  represents an individual value and
represents an individual value and 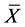 represents the mean value of a sample.
represents the mean value of a sample.
 (2)
(2)
The third statistical moment  is expressed by Equation (3).
is expressed by Equation (3).
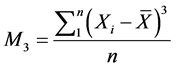 (3)
(3)
Substituting Equation (2) and Equation (3) into Equation (1), the following expression is obtained for the skewness.
 (4)
(4)
2.2. Kurtosis
Reference [14] uses the value of kurtosis in the study of failure detection in rolling bearings used in electrical motors. Their experimental results indicate that the amplitudes of the signal harmonic components do not vary expressively for rolling bearings without defects. Moreover, they state that statistical analysis using the kurtosis can show clearly the signal variations for bearings operating with defects. Reference [15] also employs kurtosis to analyze and diagnose rolling bearing failures. AE statistical analysis has also been used in machining process as it is shown in the work [16] , which presents the values of Kurtosis associated with the AE signals measured during a run of a steel drawing process.
Kurtosis is a measure of dispersion that characterizes the shape of the probability distribution. Kurtosis is associated with the fourth statistical moment of a probability distribution. Reference [17] defines Kurtosis as the ratio of the fourth moment 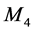 to the standard deviation σ raised to the power 4, as it is depicted in Equation (5).
to the standard deviation σ raised to the power 4, as it is depicted in Equation (5).
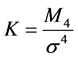 (5)
(5)
The skewness and kurtosis of the AE signal samples measured in the bump tests performed in this work are estimated to give some insights into the characteristics of the signal distribution.
3. Experimental Procedures
The description of the experimental procedures employed in this work is presented into three items: 1) Shaft assembly; 2) AE data acquisition; and 3) AE signal analysis.
3.1. Apparatus Description
Six shafts made of commercial steel AISI 1020 are used in the bump tests [18] . The basic dimensions of all shafts are shown in Figure 1. The shaft mass is 1.160 kg. The depth of the transversal crack is indicated by symbol a.
A transverse crack is etched on the shaft by machining. Section A-A in Figure 1 shows the exact location of the transverse crack introduced into the shafts. The crack depth varies from zero to the value of the shaft radius. The values of ratio μ, which relates the crack depth a to the shaft radius r, for the shafts tested are shown in Table 1.
The shaft bump tests are performed at free-free boundary conditions [10] . Both shaft ends are hanged from the test room ceiling using 0.8 mm diameter nylon wires with length of 1.2 m. An AE wideband transducer, model PAC S9208, is mounted on a special base using adhesive tape and grease within the contact surfaces. Figure 2 depicts the more important details of the shaft assembly indicating the AE sensor position and its movable base. It is highly recommended in vibration tests to mount the vibration transducer at the shaft ends to avoid some vibration mode node [10] . In acoustic emission tests such recommendation is not applicable, because the AE transducer is supposed to capture the propagating elastic waves along the shaft generated by the crack. For convenience, the AE transducer is mounted on the shaft right-hand side end, as it is indicated by Figure 2.
![]()
Figure 1. Shaft basic dimensions with typical transversal crack [18] .
![]()
Table 1. Ratio μ values for the six shafts used in this work.
![]()
Figure 2. Schematic drawing of the cracked shafts for the bump tests.
3.2. AE Instrumentation System
Each shaft undergoes five bump tests, which provide 30 AE signal samples for analysis. The bump is provided by a steel bar, which also is hanged from the ceiling using a 0.8 mm diameter nylon rope, as it is depicted in Figure 3. A small pendular motion is induced in the testing shaft when the bar hits the shaft. The impact takes place always at the same position for all shafts. To avoid large variation on the impulse caused by the bump, the hitting metallic bar is connected by means of a fixed length nylon rope to a concrete column.
The data acquistion system (DAQ) consists of an AE transducer PAC S9208, a NI deck PXI1042, a processor NI PXI 8106, a DAQ NI PXI6115 and a DAQ NI TB2708. The NI Sound and Vibation kit is used to capture the AE signals at sampling frequency of 0.4 MHz and acquisition time of 0.4 s. The signal amplitude is captured in volts. The AE data collected during the bump tests are stored in a computer for posterior analysis. The software MatLab© is employed to develop tools for analysis of the AE signal files.
3.3. AE Signal Analysis
The 30 AE signal samples are analyzed in the time-domain using the software MatLab©. The experimental data treatment is performed by using seven different approaches. In the first approach, the experimental data are treated by a Wavelet technique. Wavelet transform daubechies 4 [19] is employed in this approach. In the second approach, the AE signals are analyzed from 0.2 s to 0.4 s in all experiments, to eliminate the range of large variation at the initial testing times, in which the signal presents very high amplitudes followed by a strong decay. The curves of AE amplitude in volts versus time are the core of the third approach. The fourth approach is based on fitting a probability distribution to the time curve of AE signal. The AE signal average and standard deviation are computed for each sample. In the fifth approach, a similar statistical analysis is performed to estimate the AE signal average 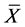 and standard deviation σ for each shaft, that is, for five samples simultaneously. The approximate normal distribution is generated for each shaft in the sixth approach. The seventh and last approach consists on the computation of the values of skewness and kurtosis for the AE data.
and standard deviation σ for each shaft, that is, for five samples simultaneously. The approximate normal distribution is generated for each shaft in the sixth approach. The seventh and last approach consists on the computation of the values of skewness and kurtosis for the AE data.
4. Results and Analysis
It is noteworthy to say that assembly of the impacting metallic bar (Figure 3) seems to be efficient enough to reduce the AE signal variations in the bump tests. Figure 4 de-
![]()
Figure 3. Schematics of the shaft test rig indicating the assembly of the bumping metallic bar.
![]()
Figure 4. Comparative curves of AE signal versus time rendered from five bump tests performed on shaft 5.
picts the AE curves rendered from the five bump tests performed on shaft 5 (µ = 0.8). The AE signal patterns are basically the same in all five bump tests.
The curves of AE amplitude distribution versus frequency for the 30 bump tests are shown in Figure 5. Curves 5.a, 5.b, 5.c, 5.d, 5.e, and 5.f depict the five curves of AE amplitude probability distribution, respectively, for shafts 1, 2, 3, 4, 5, and 6. It can be noticed that there is a spreading trend on the base of the distribution as the shaft crack increases.
Using the data from the distributions shown on Figure 5, it is possible to estimate the mean value  and the standard deviation σ associated with the AE signals for each shaft. The average and the standard deviation are computed from the data collected in the five bump tests for each shaft. Table 2 summarizes these values for all six shafts.
and the standard deviation σ associated with the AE signals for each shaft. The average and the standard deviation are computed from the data collected in the five bump tests for each shaft. Table 2 summarizes these values for all six shafts.
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)![]() (e) (f)
(e) (f)
Figure 5. Curves of AE signal probability distribution for five bump tests performed in the six shafts.
The mean value and the standard deviation from Table 2 can be used to adjust an equivalent normal distribution on the AE amplitude distribution for each shaft. The curves of AE amplitude probability distribution for each shaft are depicted in Figure 6.
![]()
Table 2. Values of average ![]() and standard deviation σ for the six shafts.
and standard deviation σ for the six shafts.
![]()
Figure 6. Comparison of equivalent normal probability distributions for six shafts.
Finally, Table 3 depicts the estimated values of kurtosis and skewness of each shaft for the AE data collected from the five bump tests. As the shaft crack depth increases (μ increases), it can be observed that the values of kurtosis and skewness decrease.
The decreasing values of kurtosis as the crack depth increases, shown in Table 3, indicate that a flattening on the AE signal amplitude peaks occurs when a crack is introduced into the shaft. This peak flattening increases as the ratio μ increases. This pattern can be seen in Figure 6. Moreover, the decreasing values of skewness as the crack size increases indicate, mathematically, that a shift on the AE amplitude peaks from the right-hand side to the left-hand side of the probability distribution takes place. This skewness shifting trend as the ratio μ increases is not apparent in Figure 6.
A very important finding in this work is the possibility of performing bump tests on rotating shafts in order to identify the crack initiation and to monitor the crack growth. The AE signal can be used to identify the presence of a crack and may even estimate the crack size. Further research is necessary to apply the same data treatment techniques on the AE signals on vibration tests performed on real operating conditions.
![]()
Table 3. Estimated values of kurtosis and skewness for the AE data rendered from each shaft.
5. Final Remarks
The AE data rendered from the several bump tests performed on cracked shafts of different crack depths are treated by wavelet transform and statistical moments to analyze the influence of the crack size on the AE signal amplitude and frequency. The preliminary results obtained in this work indicate that a decrease on the AE amplitude peaks occurs as the crack depth increases. The values of kurtosis associated with the AE data apparently are very sensitive to the detection of geometric discontinuities in the shafts tested. At first glance, the statistical treatment of AE signals obtained in bump tests could be used to identify the crack initiation and monitor the crack growth in rotating shafts.