Analysis of Optical Properties of Off-Axis Reflective Volume Holographic Grating ()


1. Introduction
In 1948, Dennis Gabor proposed the holographic wavefront reconstruction technique to reduce the aberration of electron microscopy and improve the image resolution, namely, the short wavelength electromagnetic spectrum line was used to store the measured object image, while the long wavelength electromagnetic spectrum was used to reproduce. In the field of holographic optical, holographic wavefront reconstruction is to use two beams of coherent light exposure holographic material, and the interference fringes of two beams of coherent light will be recorded in holographic material, and any beam at the original records is used to irradiate the recorded holographic material, which can reproduce another beam at the original records [1]-[6].
If the object and reference beams are both point light source and recorded in the holographic medium, the holographic medium consisting of point source hologram can be as the basic holographic optical element, which can be realized the function of the basic lens, a reflecting mirror. A point source of holographic optical elements can be a bunch of diverging or converging spherical wave and a bunch of planar light wave mutual interference, and can also two beams of spherical waves interfere with each other, or two beams of plane waves interfere with each other. The interference fringes can be a group of paraboloid, ellipsoid, hyperboloid or plane, depending on two point light source with respect to the position of the plane of the recording medium position [7]-[12].
2. Interference Field of Plane Wave and Converging Spherical Wave
According to the theory of holographic wavefront reconstruction, when object beam with the convergent spherical wave and reference beam with the parallel light is used to exposure to holographic media at different side, the converging spherical wave can be reconstruction by irradiating the reference beam on the redording holographic media, which achieves the function of focusing mirror.
The expression of complex amplitude 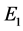 and
and  of two coherent light waves are respectively [13]:
of two coherent light waves are respectively [13]:
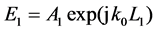 (1)
(1)
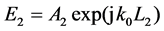 (2)
(2)
where  and
and 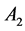 are respectively the amplitude of light wave of
are respectively the amplitude of light wave of  and
and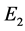 ;
; 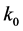 is the wave vector in the vacuum, and
is the wave vector in the vacuum, and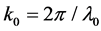 ,
, 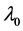 is the wavelength of light in the vacuum;
is the wavelength of light in the vacuum; 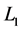 and
and 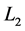 are respectively the light path of two beams.
are respectively the light path of two beams.
According to the interference principle, the two light waves meet with the same frequency, same vibration direction, which would produce interference phenomenon The distribution of the interference intensity is:
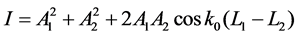 (3)
(3)
When the optical path difference is equal to the wavelength of integer times, that is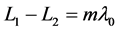 , the position would have the constructive inference.
, the position would have the constructive inference.
Assuming that a converging spherical wave E1 gathers the origin of coordinates, and the propagation direction of another plane wave E2 parallels to the YZ plane with the angle  for the z axis. Thus,
for the z axis. Thus, ![]() and
and![]() . The the location generating an constructive interference is:
. The the location generating an constructive interference is:
![]() (4)
(4)
From the Formula (4), we can see that the position of constructive interference is a group of paraboloid of revolution, which is symmetry with the beeline of![]() , but the opening towards the propagation of plane waves in the opposite direction. When the angle
, but the opening towards the propagation of plane waves in the opposite direction. When the angle ![]() between the parallel optical wave and the Z axis is zero, the pattern generating the constructive interference in the YZ plane is a parabolic, as shown in Figure 1. The parabola opening is in the negative direction of the Z axis. With the increase of the absolute value of the interference level m, the parabola opening is gradually increased. The maximum interference level is the zero, and the position of constructive interference is non positive part of the Z axis, and the minimum interference level is negative infinity. For a certain level m of interference, the parabolic peak is located at the Z axis of the
between the parallel optical wave and the Z axis is zero, the pattern generating the constructive interference in the YZ plane is a parabolic, as shown in Figure 1. The parabola opening is in the negative direction of the Z axis. With the increase of the absolute value of the interference level m, the parabola opening is gradually increased. The maximum interference level is the zero, and the position of constructive interference is non positive part of the Z axis, and the minimum interference level is negative infinity. For a certain level m of interference, the parabolic peak is located at the Z axis of the![]() , and the distance of the parabolic peak between the adjacent interference level is
, and the distance of the parabolic peak between the adjacent interference level is![]() .
.
![]()
Figure 1. Interference field of plane wave and converging spherical wave.
3. The “Curved” Coupled Wave Theory Based on “Plane” Coupled Wave Theory
In the last section, the interference fringes are formed by the signal beam and the reference beam in the holographic material, which is the basic holographic optical element, and can be called as the holographic grating [14]. According to the comparison of the thickness of the holographic recording medium and the fringe spacing of the recording, the holographic grating can be divided into volume holographic grating (thick holographic grating) or plane holographic grating (thin holographic grating). If the thickness of the holographic recording medium is equal to or greater than the recorded interference fringe interval, the interference fringe formed in the recording medium is three-dimensional distribution, namely the volume holographic grating. Due to high diffraction efficiency of volume holographic grating, so that the volume holographic optical elements are widely used in many optical system. The volume holographic optical elements at the incidence of the Bragg angle or close to the Bragg angle can obtain effective wavefront reconstruction [15]-[18].
The interference fringes formed by point source hologram in holographic medium can be divided into two kinds: the plane interference fringe and the curved interference fringe. In holographic interferogram for point source field, the only the interference fringes of one plane wave and another plane wave are planar shape. When a convergent spherical wave or divergent spherical wave is the reference beam or the signal beam, the interference fringes formed by the interference field are curved shape (paraboloid, hyperboloid, ellipsoid). The coupled wave theory proposed by Kogelnik in 1969 mainly analyzed the characteristic of the holographic grating with plane interference fringes, not analyzed the holographic grating with curved interference fringes.
Therefore, the “curved” coupled wave theory is derived in this paper, based on the “plane” coupled wave theory. The geometric structures of the base element hologram are respectively recorded by the two plane waves and the converging spherical wave and plane wave as shown in Figure 2 and Figure 3. By comparison, the direction and magnitude of grating vector kF of volume hologram recorded by two plane waves are both the same in the whole position in Figure 2, in other words, the direction and magnitude of grating vector is a constant![]() . But the grating vector kF recorded by converging spherical wave and plane wave may be different in different position, that is,
. But the grating vector kF recorded by converging spherical wave and plane wave may be different in different position, that is, ![]() is variable.
is variable.
According to the wave differential equation, after a series of deduction, the diffraction efficiency of the holographic grating is described as [15]
![]() (5)
(5)
Here,
![]() (6)
(6)
![]()
Figure 2. The volume holographic grating recorded by two plane waves.
![]()
Figure 3. The volume holographic grating recorded by converging spherical wave and plane wave.
![]() (7)
(7)
where, n1 is the refractive index of volume holographic grating, d is the thickness of volume holographic grating, is the incident light wavelength for reconstruction, cR and cS are the inclination factor of volume holographic grating, and can be described as:
![]() (8)
(8)
![]() (9)
(9)
where kF is the grating vector of volume hologram, kR is wave vector of reference beam, ![]() is the angle between the reference beam and the z aixs, and
is the angle between the reference beam and the z aixs, and ![]() is the angle between the grating vector and the z axis.
is the angle between the grating vector and the z axis.
In the Formula (7), ![]() is described as:
is described as:
![]() (10)
(10)
where n is the average refractive index of volume holographic grating.
If the incident angle ![]() of reference wave deviates from the Bragg angle of
of reference wave deviates from the Bragg angle of![]() , the incident angle can be described as
, the incident angle can be described as![]() . If the wavelength of reference wave deviates from the recording wavelength, the wavelength can be described as
. If the wavelength of reference wave deviates from the recording wavelength, the wavelength can be described as![]() . Thus, the Formula (10) can be described as
. Thus, the Formula (10) can be described as
![]() (11)
(11)
When ![]() is little, the Formula (11) can be described as:
is little, the Formula (11) can be described as:
![]() (12)
(12)
Kogelnik only analyzed the diffraction efficiency of volume holographic grating under the condition of the interference fringes are the plane by the interference of two plan waves, that is, the size kF and angle ![]() of grating vector are the same in the whole position of grating. But the kF and
of grating vector are the same in the whole position of grating. But the kF and ![]() is different in the volume holographic grating with the curved interference fringes, so the wavelength selectivity, the angle selectivity and the diffraction efficiency at arbitrary position of grating may be different. Therefore, the size and direction of the grating vector with curved interference fringes at different locations need to be given.
is different in the volume holographic grating with the curved interference fringes, so the wavelength selectivity, the angle selectivity and the diffraction efficiency at arbitrary position of grating may be different. Therefore, the size and direction of the grating vector with curved interference fringes at different locations need to be given.
Assuming that the plane wave (reference beam) is incident to the holographic media from the air with the angle of![]() , and the propagation angle in media is
, and the propagation angle in media is![]() , and the coordinate of the converging point of spherical wave is
, and the coordinate of the converging point of spherical wave is![]() , and the propagation angle of signal beam in media is
, and the propagation angle of signal beam in media is![]() , and the exit angle from the media
, and the exit angle from the media
into the air is![]() , and the coordinate of arbitrary position in media is
, and the coordinate of arbitrary position in media is![]() . Therefore, according to the theory of K vector closure, it can be deduced that the angle
. Therefore, according to the theory of K vector closure, it can be deduced that the angle ![]() and size
and size ![]() of grating vector at any point in the holographic grating with curved interference fringes.
of grating vector at any point in the holographic grating with curved interference fringes.
For the volume holographic grating of the reflection type with the curved interference fringes, the ![]() and
and ![]() are described as:
are described as:
![]() (13)
(13)
![]() (14)
(14)
4. The Optical Properties of the Off-Axis Volume Holographic Grating
The phase volume holographic grating for reflection type and no absorption with the curved interference fringes is divided into the coaxial and off-axis recordings. The reconstruction process is shown in Figure 4(a) and Figure 4(b), respectively.
Due to the surface position zF of the reflection volume holographic grating is zero, only need to analyze the characteristics of the grating when ![]() at different locations of xF.
at different locations of xF.
In Figure 4(b), assuming that the laser wavelength is 532 nm, the coordinate of the converging point of spherical wave is![]() , the incident angle of plane wave is
, the incident angle of plane wave is![]() , the range of coordinate position of holographic media is
, the range of coordinate position of holographic media is![]() ,
,![]() .
.
4.1. Angular Selectivity at Different Locations of the Volume Holographic Grating
The angular selectivity in different locations of xF for the reflection volume holographic grating with the curved interference fringes is shown in Figure 5, when xF = −10 - 10 cm, zF = 0 cm, and the thickness of grating is 20 μm, 60 μm, 100 μm, respectively.
![]()
![]() (a) (b)
(a) (b)
Figure 4. The sketch of reconstruction process of reflection volume holographic grating with the curved interference fringes recorded by the plane wave and the converging spherical wave. (a) the coaxial recording; (b) the off-axis recording.
For a certain thickness, the angular selectivity is gradually reduced and the field of view is gradually increased from xF = −10 - 10 cm. The cause is the increase of the angle between the propagation vector kR of reference beam and the propagation vector kS vector of signal beam. The relationship between angular selectivity and diffraction efficiency in the center and two edges of off-axis reflection volume holographic grating with the curved interference fringes is shown in Figure 6.
4.2. Wavelength Selectivity at Different Locations of the Volume Holographic Grating
The wavelength selectivity at different locations of off-axis volume holographic grating with the reflection type is shown in Figure 7. With the increase of the thickness of grating, the wavelength selectivity will enhance. The relationship between spectral selectivity and diffraction efficiency of in the center and two edges of off-axis reflection volume holographic grating with the curved interference fringes is shown in Figure 8.
4.3. Diffraction Efficiency at Different Locations on the Surface of the Grating
In the off-axis records, on the surface of holographic media with xF = −10 - 10 cm, zF = 0 cm, and the thickness of holographic media is respectively 20 μm, 60 μm and 100 μm, the diffraction efficiency of the reflection type volume holographic grating with curved interference fringes at different locations of xF is shown in Figure 9, when Bragg angle and recording wavelength is used to reconstruct.
When the thickness of grating is 20 μm, the diffraction efficiency is gradually reduced from xF = −10 - 10 cm. This is due to the gradual increase of the angle between the propagation vector kR of the reference beam and the propagation vector kS of the signal beam in the off-axis recording.
When the thickness of grating is 60 μm, the diffraction efficiency decreases from 100% to 99.95%.
When the thickness is 100 μm, the diffraction efficiency is 100%, which indicates that the diffraction efficiency is mainly determined by the thickness of the recording medium, and to a certain extent the angle between the propagation vector of light wave affects the diffraction efficiency.
5. Conclusion
Based on the above analysis, the angular and spectral selectivity of reflection type volume holographic grating at different locations is determined by the angle between the propagation vectors of reference beam kR and signal beam kS. The smaller the angle, the angular and spectral selection is stronger; the angle becomes larger, the angular and spectral selectivity weaker. The diffraction efficiency also meet the above conclusions for the relatively thin volume holographic grating, but the diffraction efficiency will be 100% for the relatively thick volume holographic grating.
NOTES
![]()
*Corresponding author.