Schultz Polynomials and Their Topological Indices of Jahangir Graphs J2,m ()
Received 20 June 2016; accepted 26 August 2016; published 29 August 2016

1. Introduction
Let G = (V; E) be an undirected connected graph without loops or multiple edges. The sets of vertices and edges of G are denoted by V(G) and E(G), respectively. A topological index is a numerical quantity derived in an unambiguous manner from the structure graph of a molecule. As a graph structural invariant, i.e. it does not depend on the labelling or the pictorial representation of a graph. Various topological indices usually reflect molecular size and shape. An oldest topological index in chemistry is the Wiener index, that first introduced by Harold Wiener in 1947 to study the boiling points of paraffin. It plays an important role in the so-called inverse structure-property relationship problems. The Wiener index of a molecular graph G was defined as [1] :
 (1)
(1)
In 1989, H.P. Schultz [13] has introduced a graph theoretical descriptor for characterizing alkanes by an integer number as follow:
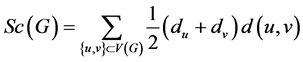 (2)
(2)
where du and dv are degrees of vertices u and v. Schultz named this descriptor the “molecular topological index” and denoted it by MTI. Later MTI became much better known under the name the Schultz index.
In 1997, S. Klavžar and I. Gutman [14] defined another based structure descriptors the Modified Schultz index of G is defined as:
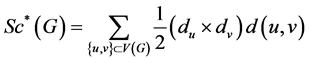 (3)
(3)
Now, there are two topological polynomials of a graph G as follow:
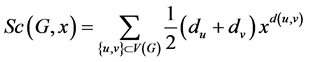 (4)
(4)
and
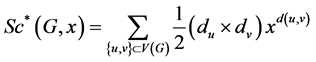 (5)
(5)
For more details about the Schultz, Modified Schultz polynomials and their topological indices and other molecular topological polynomials and indices reader can see the paper series [13] - [29] .
In this paper we study the Schultz, Modified Schultz polynomials and their topological indices of Jahangir graphs J2,m for all integer number m ≥ 3.
2. Main Results
In this section we compute the Schultz, Modified Schultz polynomials and their topological indices for Jahangir graphs J2,m "m ≥ 3. The general form of Jahangir graphs Jn,m is defined as follows:
Definition 1. [30] - [35] Jahangir graphs Jn,m for m ≥ 3, is a graph on nm + 1 vertices i.e., a graph consisting of a cycle Cnm with one additional vertex which is adjacent to m vertices of Cnm at distance n to each other on Cnm.
Theorem 1. Let J2,m be the Jahangir graphs ("m ≥ 3). Then,
The Schultz polynomial of J2,m is equal to
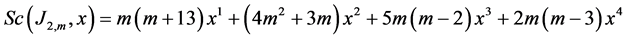
The Modified Schultz polynomial of J2,m is equal to

Proof. "m ≥ 3 consider Jahangir graph J2,m. By using Definition 1 and [29] - [32] , one can see that the number
of vertices in Jahangir graph J2,m is equal to 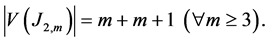 And the number of edges of Ja-
And the number of edges of Ja-
hangir graph J2,m is equal to 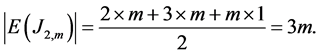 Because, there is only Center vertex with
Because, there is only Center vertex with
degree m and there are m vertices with degree 2 and m vertices with degree. In this paper, we denote the sets of all vertices with degree two by A, all vertices with degree three by B and only Center vertex c by C.
From the structure of Jahangir graph J2,m (Figure 1), we see that there are distances from one to four, for every vertices  In other words,
In other words, 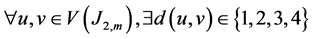 and the Diameter D of Jahangir graph J2,m is equal to D(J2,m) = 4.
and the Diameter D of Jahangir graph J2,m is equal to D(J2,m) = 4.
I. If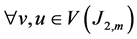 ,
, ![]() , we have two case for first sentences of the Schultz, Modified Schultz polynomials of J2,m.
, we have two case for first sentences of the Schultz, Modified Schultz polynomials of J2,m.
I-1. For a vertex![]() , there are two path with length one until a vertex
, there are two path with length one until a vertex![]() , thus there are 2m edges uvÎE(J2,m), such that
, thus there are 2m edges uvÎE(J2,m), such that![]() ,
,![]() . Therefore, we have two terms 5 × 2mx1, 6 × 2mx1 of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m, respectively.
. Therefore, we have two terms 5 × 2mx1, 6 × 2mx1 of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m, respectively.
I-2. For only vertex![]() , there are m path with length one until a vertex
, there are m path with length one until a vertex![]() , thus there are m edges
, thus there are m edges![]() , such that
, such that![]() ,
,![]() . So, we have two terms
. So, we have two terms ![]() and
and ![]() of the Schultz and Modified Schultz polynomials of J2,m, respectively.
of the Schultz and Modified Schultz polynomials of J2,m, respectively.
Thus, the first sentences of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m are equal to
![]() and
and![]() , respectively.
, respectively.
II. If![]() ,
, ![]() , we have three case for first sentences of the Schultz, Modified Schultz polynomials of J2,m.
, we have three case for first sentences of the Schultz, Modified Schultz polynomials of J2,m.
II-1. For a vertex![]() , there are two path with length two until other vertices A, so there are (1/2) × 2m 2-edge-path in J2,m, such that
, there are two path with length two until other vertices A, so there are (1/2) × 2m 2-edge-path in J2,m, such that![]() . Therefore, we have a terms 4 × mx2 of the Schultz and Modified Schultz polynomials of J2,m.
. Therefore, we have a terms 4 × mx2 of the Schultz and Modified Schultz polynomials of J2,m.
II-2. For every vertex![]() , there are only 2-edge-path until the Center vertex c, and there are m
, there are only 2-edge-path until the Center vertex c, and there are m
2-edge-path in J2,m with ![]() and
and![]() . Therefore, we have two terms
. Therefore, we have two terms![]() , 2m × mx2 of the Schultz and Modified Schultz polynomials of J2,m, respectively.
, 2m × mx2 of the Schultz and Modified Schultz polynomials of J2,m, respectively.
II-3. For a vertex![]() , there are m − 1 path with length two until other vertices
, there are m − 1 path with length two until other vertices![]() , so there are
, so there are ![]() 2-edge-path in J2,m, such that
2-edge-path in J2,m, such that![]() ,
,![]() . So, we have two terms
. So, we have two terms ![]() and
and ![]() of the Schultz and Modified Schultz polynomials of J2,m, respectively.
of the Schultz and Modified Schultz polynomials of J2,m, respectively.
Thus, the second sentences of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m are equal
to ![]() and
and ![]() respectively.
respectively.
III. If![]() ,
, ![]() , for a vertex
, for a vertex![]() , there are (m − 2)m path with length three until vertices of B, such that
, there are (m − 2)m path with length three until vertices of B, such that![]() ,
,![]() . Therefore, we have two sentences
. Therefore, we have two sentences ![]() and
and ![]() of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m, respectively.
of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m, respectively.
IV. If![]() ,
, ![]() , for a vertex
, for a vertex![]() , there are m − 3 path with length 4 = D(J2,m), between v and other vertices u of A. Thus by
, there are m − 3 path with length 4 = D(J2,m), between v and other vertices u of A. Thus by![]() , the fourth sentence of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m is equal to
, the fourth sentence of the Schultz and Modified Schultz polynomials of Jahangir graph J2,m is equal to![]() .
.
From the definition of the Schultz, Modified Schultz polynomials and above mentions, we have following results "m Î ℕ − {2}.
![]()
Figure 1. Jahangir graphs J2,4, J2,5, J2,6, J2,16 and J2,32 [32] .
![]() (6)
(6)
and
![]() (7)
(7)
And these complete the proof. ![]()
Theorem 2. Let J2,m be the Jahangir graphs ("m ≥ 3). Then, the Schultz, Modified Schultz indices of J2,m are equal to
![]()
Proof. Consider the Jahangir graph J2,m ("m ≥ 3) that presented in above proof. Now, by using the results from proof of Theorem 1 and according to the definitions of the Schultz, Modified Schultz indices of the graph G, one can see that these indices are the first derivative of their polynomials (evaluated at x = 1). Thus we have following computations "m Î ℕ − {2}.
![]() (8)
(8)
And
![]() (9)
(9)
Here the proof of theorem is completed. ![]()
Acknowledgements
The author is thankful to Professor Emeric Deutsch from Department of Mathematics of Polytechnic University (Brooklyn, NY 11201, USA) for his precious support and suggestions.
NOTES
![]()
*Corresponding author.