Razumikhin-Type Theorems on General Decay Stability of Impulsive Stochastic Functional Differential Systems with Markovian Switching

Zhiyu Zhan, Caixia Gao

School of Mathematical Sciences, Inner Mongolia University, Hohhot, China.

DOI: 10.4236/jamp.2016.48172                

Abstract

In this paper, the Razumikhin approach is applied to the study of both p-th moment and almost sure stability on a general decay for a class of impulsive stochastic functional differential systems with Markovian switching. Based on the Lyapunov-Razumikhin methods, some sufficient conditions are derived to check the stability of impulsive stochastic functional differential systems with Markovian switching. One numerical example is provided to demonstrate the effectiveness of the results.

Keywords

Impulsive Stochastic Functional Differential System, p-th Moment Stability, Almost Sure Stability, Lyapunov-Razumikhin Approach

Received 8 July 2016; accepted 26 August 2016; published 29 August 2016

1. Introduction

Impulsive stochastic systems with Markovian switching is a class of hybrid dynamical systems, which is composed of both the logical switching rule of continuous-time finite-state Markovian process and the state represented by a stochastic differential system [1] . Because of the presence of both continuous dynamics and discrete events, these types of models are capable of describing many practical systems in many areas, including social science, physical science, finance, control engineering, mechanical and industry. So this kind of systems have received much attention, recently (for instance, see [2] - [5] ).

It is well-known that stability is the major issue in the study of control theory, one of the most important techniques applied in the investigation of stability for various classes of stochastic differential systems is based on a stochastic version of the Lyapunov direct method. However, the so-called Razumikhin technique combined with Lyapunov functions has also been a powerful and effective method in the study of stability. Recalled that Razumikhin developed this technique to study the stability of deterministic systems with delay in [6] [7] , then, Mao extended this technique to stochastic functional differential systems [8] . This technique has become very popular in recent years since it is extensively applied to investigate many phenomena in physics, biology, finance, etc.

Mao incorporated the Razumikhin approach in stochastic functional differential equations [9] and in neutral stochastic functional differential equations [10] to investigate both p-th moment and almost sure exponential stability of these systems (see also [11] - [13] , for instance). Later, this technique was appropriately developed and extended to some other stochastic functional differential systems, especially important in applications, such as stochastic functional differential systems with infinite delay [14] - [16] , hybrid stochastic delay interval systems [17] and impulsive stochastic delay differential systems [18] - [20] . Recently, some researchers have introduced y-type function and extended the stability results to the general decay stability, including the exponential stability as a special case in [21] - [23] , which has a wide applicability.

In the above cited papers, both the p-th moment and almost sure stability on a general decay are investigated, but mostly used in stochastic differential equations. And As far as I know, a little work has been done on the impulsive stochastic differential equations or systems. In this paper, we will close this gap by extending the general decay stability to the impulsive stochastic differential systems. To the best of our knowledge, there are no results based on the general decay stability of impulsive stochastic delay differential systems with Markovian switching. And the main aim of the present paper is attempt to investigate the p-th moment and almost sure stability on a general decay of impulsive stochastic delay differential systems with Markovian switching. Since the delay phenomenon and the Markovian switching exists among impulsive stochastic systems, the whole systems become more complex and may oscillate or be not stable, we introduce Razumikhin-type theorems and Lyapunov methods to give the conditions that make the systems stable. By the aid of Lyapunov-Razumikhin approach, we obtain the p-th moment general decay stability of impulsive stochastic delay differential systems with Markovian. In order to establish the criterion on almost surely general decay stability of impulsive stochastic delay differential systems with Markovian, the Holder inequality, Burkholder-Davis-Gundy inequality and Borel- Cantelli’s lemma are utilized in this paper.

The paper is organized as follows. Firstly, the problem formulations, definitions of general dacay stability and some lemmas are given in Section 2. In Section 3, the main results on p-th moment and almost sure stability on a general decay of impulsive stochastic delay differential systems with Markovian switching are obtained with Lyapunov-Razumikhin methods. An example is presented to illustrate the main results in Section 4. In the last section the conclusions are given.

2. Preliminaries

Throughout this paper, let 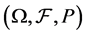be a complete probability space with some filtration 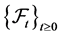satisfying the usual condition (i.e., the filtration is increasing and right continuous while 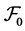contain all P-null sets). Let be an m-dimensional -adapted Brownian motion.

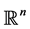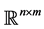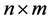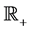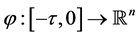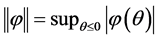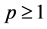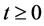Let be the n-dimensional Euclidean space; denotes the real matrix space; is the set of all non-negative real numbers; denotes the family of continuous functions with the norm; denotes the standard Euclidean norm for vectors; let, ,) denotes the family of -measurable -valued random variables such that and be the -measur- able -valued random variables; means the expectation of a stochastic process; is a discrete index set, where N is a finite positive integer.

Let, be a right-continuous Markov chain on the probability space taking values in a finite state space with generator given by

where, and is the transition rate from i to j if while.

We assume that the Markov chain is independent of the Brownian motion. It is well known that almost every sample path of is a right-continuous step function with a finite number of simple in any subinterval if. In other words, there exist a sequence of stopping times almost surely such that is a constant in every interval for any, i.e.

In this paper, we consider the following impulsive stochastic delay differential systems with Markovian switching

(1)

where the initial value

represents the impulsive perturbation of x at time. The fixed moments of impulse times satisfy (as),.

For the existence and uniqueness of the solution we impose a hypothesis:

Assumption (H): For and satisfy the local Lipschitz condition and the linear growth condition. That is, there exist a constant such that

For all, and, and, moreover, there are a constant such that

For all, and.

Definition 1 is said to be y-type function, if it satisfies the following conditions:

(1) It is continuous, monotone increasing and differentiable;

(2) and;

(3).

(4) for any.

Definition 2 For, impulsive stochastic delay differential systems with Markovian switching (1) is said to be p-th moment stable with decay of order, if there exist positive constants and function, such that

(2)

when, we say that it is stable in mean square, when, we say that it is p-th moment exponential stable, when, we say that it is p-th moment polynomial stable.

Definition 3 impulsive stochastic delay differential systems with Markovian switching (1) is said to be almost surely stable with decay of order, if there exist positive constant and function, such that

(3)

when, we say that it is almost surely exponential stable, when, we say that it is almost surely polynomial stable.

Let denote the family of all nonnegative functions on that are continuously once differentiable in t and twice in x. For each define an operator for system (1) by

where

Lemma 1 (Burkholder-Davis-Cundy inequality) Let, , there exist positive constants and, such that

where

Lemma 2 (Borel-Cantelli’s lemma)

(1) If and, then

That is, there exist a set with and an integer valued random variable such that for every we have whenever.

(2) If the sequence is independent and, then

That is, there exists a set with, such that for every, there exists a sub-seq- uence such that the belongs to every.

3. Main Results

In this section, we shall establish some criteria on the p-th moment exponential stability and almost exponential stability for system (1) by using the Razumikhin technique and Lyapunov functions.

Theorem 1 For systems (1), let (H) hold, and is a y-type function, Assume that there exist a function, positive constants and such that

(H₁) For all

(4)

(H₂) For all

(5)

For all and those satisfying

(6)

where.

(H₃) For all and

(7)

where and.

Then, for any initial, there exists a solution on to system (1). Moreover, the system (1) is p-th moment exponentially stable with decay of order.

Proof. Fix the initial data arbitrarily and write simply. When is replaced by, if we can prove that the system (1) is p-th moment exponentially stable with decay of order for all, then the desired result is obtained. Choose satisfying , and thus we can have the following fact:

Then it follows from condition (H₁) that

In the following, we will use the mathematical induction method to show that

(8)

In order to do so, we first prove that

(9)

This can be verified by a contradiction. Hence, suppose that inequality (9) is not true, than there exist some such that. Set

. By using the continuity of in

the interval, then and

(10)

(11)

Define, then and

(12)

(13)

Consequently, for all, we have

And so

By condition (H₂) we have

Consequently,

(14)

Applying the formula to yields

(15)

By condition (14), we obtain

(16)

On the other hand, a direct computation yields

that is

which is a contradiction. So inequality (9) holds and (8) is true for. Now we assume that (8) is satisfied for, i.e. for every,

(17)

Then, we will prove that (8) holds for,

(18)

Suppose (18) is not true, i.e. there exist some such that

(19)

Then, it follows from the condition (H₃) and (17) that

which implies that the dose not satisfy the inequality (19). And from this, set

. By the continuity of in the

interval, we know that and

(20)

(21)

Define, then and

(22)

(23)

Fix any, when for all, then (20)-(22) imply that

If for some, we assume that, without loss of generality, , for some, then from (17) and (20)-(22), we obtain

(24)

Therefore,

by condition (H₂) we have

Consequently,

(25)

Similar to (15), applying the formula to yields

By condition (25), we obtain

On the other hand, by (20) and (22), we have

that is

which is a contradiction. So inequality (18) holds. Therefore, by mathematical induction, we obtain (8) holds for all. Then from condition (H₁), we have

which implies

i.e., system (1) is pth moment exponentially stable with decay of order. The proof is complete.

Theorem 2 For system (1), suppose all of the conditions of Theorem 1 are satisfied. Let, assume that there exist constants, such that for all and,

(26)

Then, for any initial and for any, there exists a solution on to stochastic delay nonlinear system (1). Moreover, the system (1) is almost surely stable with decay of order and

(27)

Proof. Fix the initial data arbitrarily and write simply. We claim that

(28)

where

Choose sufficiently small and, for the fixed, let, where

is the maximum integer not more than x. Then for any, there exist positive integer i, , such that. So, for any, , we obtain

(29)

For each i when, , we obtain

(30)

By Theorem 1, we have

(31)

By Holder inequality, condition (26) and Theorem 1, we derives that

(32)

Similarly, by the Lemma 1 and (32), we obtain

(33)

where is a positive constant dependent on p only.

Substituting (31), (32) and (33) into (30) yields

(34)

Thus, it follows from (29) and (34), we obtain

Using Chebyshev inequality, we have

Since, by Lemma 2, when, , we obtain

That is

Figure 1. State of the example.

Figure 2. Markovian switching of the example.

Thus, the system (1) is almost surely stable with decay of order.

4. Examples

In this section, a numerical example is given to illustrate the effectiveness of the main results established in Section 3 as follows. Consider an impulsive stochastic delay system with Markovian switching as follows

(35)

where is a right-continuous Markov chain taking values in with generator

And independent of the scalar Brownian motion, ,

, , ,.

Choosing, , , , then, ,

, then we have

and

By Theorem 1, we know that, which means that the conditions of Theorem 1 are satisfied. So the impulsive stochastic delay system with Markovian switching is p-th moment stable with decay of order 2. The simulation result of system (35) is shown in Figure 1, and the Markovian switching of system (35) is described in Figure 2.

5. Conclusion

In this paper, p-th moment and almost surely stability on a general decay have been investigated for a class of impulsive stochastic delay systems with Markovian switching. Some sufficient conditions have been derived to check the stability criteria by using the Lyapunov-Razumikhin methods. A numerical example is provided to verify the effectiveness of the main results.

Acknowledgements

The work was supported by the National Natural Science Foundation of China under Grant 11261033, and the Postgraduate Scientific Research Innovation Foundation of Inner Mongolia under Grant 1402020201336.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Ji, Y. and Chizeck, H. (1990) Controllability, Stabilizability and Continuous Time Markovian Jump Linear Quadratic Control. IEEE Transactions on Automatic Control, 35, 777-788. http://dx.doi.org/10.1109/9.57016
[2]	Liu, Z. and Peng, J. (2009) p-Moment Stability of Stochastic Nonlinear Delay Systems with Impulsive Jump and Markovian Switching. Stochastic Analysis and Applications, 27, 911-923. http://dx.doi.org/10.1080/07362990903136439
[3]	Dong, Y., Wang, Q. and Sun, J. (2009) Guaranteed Cost Control for a Class of Uncertain Stochastic Impulsive Systems with Markovian Switching. Stochastic Analysis and Applications, 27, 1174-1190. http://dx.doi.org/10.1080/07362990903259421
[4]	Sathananthan, S., Jameson, N., Lyatuu, I. and Keel, L.H. (2012) Hybrid Impulsive State Feedback Control of Markovian Switching Linear Stochastic Systems. Communications in Applied Analysis, 16, 665-686.
[5]	Sathananthan, S., Jameson, N., Lyatuu, I. and Keel, L.H. (2013) Hybrid Impulsive Control of Stochastic Systems with Multiplicative Noise under Markovian Switching. Stochastic Analysis and Applications, 31, 894-911. http://dx.doi.org/10.1080/07362994.2013.817254
[6]	Razumikhin, B.S. (1956) On the Stability of Systems with Delay. Prikl. Mat. Mekh, 20, 500-512.
[7]	Razumikhin, B.S. (1960) Application of Lyapunov’s Method to Problems in the Stability of Systems with a Delay. Automat, i Telemekh, 21, 740-749.
[8]	Mao, X. (1997) Stochastic Differential Equations and Applications. Horwood Publications, Chichester.
[9]	Mao, X. (1996) Razumikhin-Type Theorems on Exponential Stability of Stochastic Functional Differential Equations. Stochastic Processes and their Applications, 65, 233-250. http://dx.doi.org/10.1016/S0304-4149(96)00109-3
[10]	Mao, X. (1997) Razumikhin-Type Theorems on Exponential Stability of Neutral Stochastic Functional Differential Equations. SIAM Journal on Mathematical Analysis, 28, 389-401. http://dx.doi.org/10.1137/S0036141095290835
[11]	Shsikhet, L. (2013) Lyapunov Functionals and Stability of Stochastic Functional Differential Equations. Springer International Publishing, Switzerland. http://dx.doi.org/10.1007/978-3-319-00101-2
[12]	Kloeden, P.E. and Platen, E. (1992) Numerical Solution of Stochastic Differential Equations. Springer-Verlag, Berlin Heidelberg.
[13]	Huang, L. and Deng, F. (2009) Razumikhin-Type Theorems on Stability of Stochastic Retarded Systems. International Journal of Systems Science, 40, 73-80. http://dx.doi.org/10.1080/00207720802145478
[14]	Yang, Z., Zhu, E., Xu, Y., et al. (2010) Razumikhin-Type Theo-rems on Exponential Stability of Stochastic Functional Differential Equations with Infinite Delay. Acta Applicandae Mathe-maticae, 111, 219-231. http://dx.doi.org/10.1007/s10440-009-9542-1
[15]	Pavlovic, G. and Jankovic, S. (2012) Razumikhin-Type Theorems on General Decay Stability of Stochastic Functional Differential Equations with Infinite Delay. Journal of Computational and Applied Mathematics, 236, 1679-1690. http://dx.doi.org/10.1016/j.cam.2011.09.045
[16]	Wei, F. and Wang, K. (2007) The Existence and Uniqueness of the Solution for Stochastic Functional Differential Equations with Infinite Delay. Journal of Mathematical Analysis and Applications, 331, 516-531. http://dx.doi.org/10.1016/j.jmaa.2006.09.020
[17]	Mao, X., Lam, J., Xu, S. and Gao, H. (2006) Razumikhin Method and Exponential Stability of Hybrid Stochastic Delay Interval Systems. Journal of Mathematical Analysis and Applications, 314, 45-66. http://dx.doi.org/10.1016/j.jmaa.2005.03.056
[18]	Cheng, P. and Deng, F. (2010) Global Exponential Stability of Impulsive Stochastic Functional Differential Systems. Statistics and Probability Letters, 80, 1854-1862. http://dx.doi.org/10.1016/j.spl.2010.08.011
[19]	Wu, X., Zhang, W. and Tang, Y. (2013) Pth Moment Stability of Impulsive Stochastic Delay Differential Systems with Markovian Switching. Communications in Nonlinear Science and Numerical Simulation, 18, 1870-1879. http://dx.doi.org/10.1016/j.cnsns.2012.12.001
[20]	Peng, S. and Jia, B. (2010) Some Criteria on pth Moment Stability of Impulsive Stochastic Functional Differential Equations. Statistics and Probability Letters, 80, 1085-1092. http://dx.doi.org/10.1016/j.spl.2010.03.002
[21]	Hu, S., Huang, C. and Wu, F. (2008) Stochastic Differential Equations. Science Press, Beijing.
[22]	Wu, F. and Hu, S. (2012) Razumikhin-Type Theorems on General Decay Stability and Robustness for Stochastic Functional Differential Equations. International Journal of Robust and Nonlinear Control, 22, 763-777. http://dx.doi.org/10.1002/rnc.1726
[23]	Pavlovic, G. and Jankovic, S. (2012) Razumikhin-Type Theorems on General Decay Stability of Stochastic Functional Differential Equations with Infinite Delay. Journal of Computational and Applied Mathematics, 236, 1679-1690. http://dx.doi.org/10.1016/j.cam.2011.09.045