A Heuristic on Risk Management System in Goods Transportation Model Using Multi-Optimality by MODI Method ()
Received 15 July 2016; accepted 23 August 2016; published 26 August 2016

1. Introduction
The efficient goods transportation system has been recognized as an essential determinant in providing consistent, quality service to beneficiaries. A standard transport system satisfies three of the “rights” of supply. That is getting the goods there at the right time, in the right condition and in a cost effective manner. Considering this assumption into a series of actionable steps, and successfully implementing those steps, will ensure timely and effective delivery of humanitarian assistance. In that case, the safety issue is one of the important parts to transport goods from factory or source to beneficiaries. The various ways of transportation system have many kinds of risks to transport goods. Transporting goods to the beneficiaries safely and timely is a big challenge in a business sector. Some of common risks are involved in about all ways of routes such as highway, waterway, airway, railway etc. Numerous distinct techniques are utilized in unique kinds of transportation system to reduce risks.
To minimize risks in the goods transportation system, many heuristics techniques have been presented in the literature. Jamroz et al. [1] represented the four modes of transport listed in the project called Integrated System of Transport Safety ZEUS and also presented the background conditions for the integration of risk management in transport and a concept of an integrated method for risk management called TRANS-RISK. Bemeleit et al. [2] proposed a proactive risk management (RM) system to supplement a holistic process management in order to handle the existing risks of logistic systems and especially for sensitive goods. Palšaitis et al. [3] evaluate the risk when investing into infrastructure reconstruction is to safeguard heavyweight or oversized goods transportation for managing Transportation Risk in Heavyweight and Oversized Cargo service. Conca et al. [4] analyzed the interactions between road traffic flow and frequency of accidents and proposed an integrated approach for the study of routing problems considering safety in a Road Transportation of Dangerous Goods. Degirmenci et al. [5] proposed an Integrated Approach for Intermodal Transport Security and some others like [6] - [8] .
In this paper, we proposed a technique to reduce the transport risks which are applicable in all general transportation systems. The main significance of the study is to transport goods safely and timely to protect the losses of wealth, invest and the lives. Most importantly, it keeps up the reputations of the supplier of goods and makes sure for the next work order. The best way to do this is the applying of mathematical and computational methods and techniques.
2. Risk Management System in Transportation Sector
Protecting goods from some not unusual risks while transporting from sources to destinations are the major concern in the transport sector. Further the scheduled time given by the recipient for delivery should be retained for attaining next work order. In this paper, the process or system which reduces the risks to transport goods timely and safely is termed as a Risk Management System.
Risk Factors in Transportation System
The common risks which may hamper the shipment process by delaying the shipment or damaging the goods or part of goods in each of the way of transportation system are termed as risk factors. Some of these common risks are in follows:
・ Traffic: The traffic is taken into consideration to be the foremost trouble in the shipping system due to the fact whilst a distributor spends more time in traffic there are more possibilities to delays within the delivery of products or miss the ships or airplanes. This will also lead to the cancellation of the work orders and ultimately a company will lose those precise clients. So it’s far usually better to keep away from congested routes whilst shipping goods from resources to destinations.
・ Accidents: Accidents are the next catastrophe and unpredictable troubles to transport any professional or valuable goods. During accidents there are equal losses to each the service providers and the clients by using those services. There may also be loss of the lives of the drivers, breakage of the transported goods, and many others.
・ Natural Disasters and Animals: A few issues, like the natural screw ups and troubles created by using animals are something that are far from the knowledge of the human and that can't be controlled. For instance, whilst there is heavy rain, flood or landslide this may in reality lead to many unpredictable problems. Even animals cause many troubles on highways by way of making groups and standing on the highways and blockading the roads.
・ Security in Highway: Security is another issue for hampering the transportations of goods. All highways are not secured from the robbery, hijacking or kidnapping, and many others due to lacking of sufficient traffic police or police check post or coast guards. For those risks shipment may be delayed and the provider and clients each will be affected.
・ Turmoil/Political Violence/Terrorism: Political risks are affecting all the system of the country, mainly inside the business sector and within the transportation sector. Political violence may be occurring in the whole country or in some special zones. In the business sector, the transportation system will be more affected by holding transportation or destroying or damaging the vehicles, blocking roads. For that reasons shipment may be behind schedule and then goods had been spoiled via this violence.
・ Bad Condition of Routes: The conditions of the routes are the most important part for shipping goods in time and safely. Sometimes roads are bumpy or rough which affect the time schedule to shipping goods to the clients. Rough roads reduce the vehicle speed and also once in a while it has a hazard to make an accident. The weather is another trouble of transportation. Flood, heavy rain or wind or fog, thunderstorm, freezing rain, snow, and heat wave, etc. may hamper the schedule time of shipment.
・ Labor Rate Uncertainty: Labor rate associated with the transportation sector varies zone to zone and route to route. And this rate is not the same for all the seasons or time. It can be rises for lacking of labor or the most economical inflation. This uncertainty increases the total transportation cost and aftermath it will decrease the profit. If it’s far viable to reduce the routes then it may be lessen the chance of this uncertainty.
So, these are some of the factors affecting a smooth transportation of goods over an extended distance.
3. Importance of Minimization of Routes
The transportation risks are uncertain to predict the chance of occurring. Also some risk factors are unpredictable and sometimes cannot avoid some of these risks. In that situation, it is better to avoid these types of routes or if possible reduce the number of transported routes. For that the probability of the chance of happening that risks factors will be minimized. Each of the routes involves with these above discussed risks to transport goods from sources to destinations. If it is possible to minimize the number of routes to transport goods then it reduces the probability of happening those above threats. That’s mean minimizing transport routes, minimize the transport risks.
4. Minimization of Routes
Each of the transportation problems (TP) has unique optimal solutions with unique transport cost but the transport routes. It is possible to find more than one set of optimal transport routes which has the same optimal transport cost. In this paper, we are using the Modified Distribution Method (MODI) to find the multiple optimal solutions of some transportation problems to minimize the possible routes. We refashioned the MODI method to obtain multiple optimal solutions according to reducing the transport routes.
4.1. Algorithm of Modified Distribution Method (MODI)
The modified distribution method, also known as MODI method or (u − v) method provides a minimum cost solution to the transportation problem.
・ Step-1: Determine an initial basic feasible solution using any of the transportation algorithms such as North West Corner Rule (NWC), Least Cost Method (LCM), Vogel’s Approximation Method (VAM), Implied Cost Method (ICM) [9] , Lowest Allocation Method (LAM) [10] , and, or some other methods mentioned in the reference [11] - [22] etc.
・ Step-2: Determine the values of dual variables ui and vj, using .
.
・ Step-3: Compute the opportunity cost using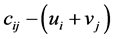 .
.
・ Step-4: Check the sign of each opportunity cost. If the opportunity costs of all the unoccupied (unallocated) cells are either positive or zero, the given solution is the optimal solution. On the other hand, if one or more unoccupied cell has negative opportunity cost, the given solution is not an optimal solution and further savings in transportation cost are possible.
・ Step-5: Select the unoccupied cell with the smallest negative opportunity cost as the cell to be included in the next solution.
・ Step-6: Draw a closed path or loop for the unoccupied cell selected in the previous step with all corner of the loop have the occupied (allocated) cells. Please note that the right angle turn in this path is permitted only at occupied cells and at the original unoccupied cell.
・ Step-7: Assign alternate plus and minus signs at the unoccupied cells on the corner points of the closed path with a plus sign at the cell being evaluated.
・ Step-8: Determine the maximum number of units that should be shipped to this unoccupied cell. The smallest value with a negative position on the closed path indicates the number of units that can be shipped to the entering cell. Now, add this quantity to all the cells on the corner points of the closed path marked with plus signs, and subtract it from those cells marked with minus signs. In this way, an unoccupied cell becomes an occupied cell.
・ Step-9: Repeat the whole procedure until an optimal solution is obtained.
4.2. Multiple Optimal Solutions Using MODI
By the MODI algorithm, when the opportunity costs of all the unoccupied cells are positive, then the solution is optimal and there is no scope to enter any unoccupied cell to be occupied. But we observed that when any of the unoccupied cells contain zero opportunity cost (other unoccupied cells should be positive) then it is possible to exchange the occupied cells with the unoccupied cells. In this case the total transport cost will not be changed but the decision variables (or routes) may be changed. And sometimes number of decision variables (or routes) decreases than previous optimal solution.
For obtaining multiple optimal solutions, when any of the unoccupied cells contain zero opportunity cost (other unoccupied cells should be positive) then repeats step-5 to step-8 for MODI algorithm.
Now let us consider a transportation problem and find the initial feasible solution (IFS) by Least Cost Method (LCM) and optimal solution by MODI.
By the Least Cost Method (LCM) allocations are made in the cell along with the minimum transport cost and adjust the supply and demand for this associate row and column by allocating the minimum amount of them. The satisfied row or column will be crossed out. If for any cell, the row and column are satisfied simultaneously, then keep one row or column with zero supply or demand amount and another will be crossed out (The crossed out row or columns are marked by the shadow in below). Iterations 1-7 show the step by step solution obtained by Least Cost Method (LCM) of the TP in Table 1.
All cells are satisfied by the supply and demand constrains. The final initial feasible solution of this transportation problem is in Table 1.
Now let us check if this above solution in Table 2 is optimal or not, if not, then make it optimal by the Modified
Iteration 1. Allocating maximum available transported amount in the least cost cell (S3, D2).
Iteration 2. Allocating maximum available transported amount in the least cost cell (S4, D4).
Iteration 3. Allocating maximum available transported amount in the least cost cell (S2, D5).
Iteration 4. Allocating maximum available transported amount in the least cost cell (S3, D5).
Iteration 5. Allocating maximum available transported amount in the least cost cell (S3, D3).
Iteration 6. Allocating maximum available transported amount in the least cost cell (S4, D3).
Distribution Method (MODI) as shown in Iteration 8 and Iteration 9, which described in the Section 4.1.
We observed that by the algorithm of MODI the above solution is optimal. The optimal solution of this
Iteration 7. Allocating maximum available transported amount in the least cost cell (S3, D1)
Iteration 8. Computedual variables ui and vj, using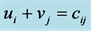 .
.
Iteration 9. Compute the opportunity cost using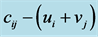 .
.
transportation problem is given below.
Table 3 represents the last iteration of checking optimality by MODI and observed that all opportunity costs (left bottom corner within parenthesis) are positive or zero. Therefore, Table 3 shows the optimal solution of the given transportation problem. There are eight routes to transport commodities satisfying supply demand constraints. The graphical representation of the above optimal result is shown in Figure 1.
Also, we observed that from Table 3, in (S4, D2) cell the opportunity cost is zero. By the existing algorithm of MODI, this solution is optimal. But if we refashion the MODI algorithm that if the opportunity cost is zero,
![]()
Table 1. The transportation problem table.
![]()
Table 2. Initial feasible solution of the above transportation problem by Least Cost Method (LCM).
![]()
Table 3. Optimal solution by Modified Distribution Method (MODI).
then repeat the step-5 to step-8 of MODI algorithm and can find another new optimal solution. The optimal cost of the new solution will not be different, but sometimes this new solution contains fewer routes than the previous solution to transport goods which minimize the risks associated with in about all ways of routes which are discussed in Section 2.1.
Now we select the (S4, D2) cell as a new occupied cell and make a closed loop with all right angle turn has an occupied cell. That is the closed loop is made by (S4, D2), (S4, D3), (S3, D3) and (S3, D2) cells. And assign alternate plus minus sign from (S4, D2) cell with a plus sign. Select the minimum amount from minus sign cells and adding this amount into plus sign cells and subtract from minus sign cells.
In Table 4, all minus sign cells have the same amount of allocation, therefore these two minus sign cells will be leave from the next iteration and (S4, D2) cell will be enter.
Thus Table 5 is the new optimal solution with seven positive allocations, that’s mean seven routes which is less than the previous optimal solution. Figure 2 shows the difference between the previous optimal result and the new optimal result.
5. Risk Minimization Using Multi-Optimality
From the above technique, we minimize transport routes to find multiple optimal solutions by the refashioned MODI method for the given transportation problems. And we observed that alternative optimal solutions contain minimal routes than the original optimal solution which will be minimize the probable risks associated with all ways of routes what are discussed earlier. Figure 3 shows the graphical representation of the comparing between the two optimal results and it clearly described that the refashioned MODI method can minimize the transport routes.
6. Illustrating Some Examples
Now we construct some numerical example to establish our proposed technique. We consider some transportation problem and find the initial feasible solutions by various transportation algorithms and then find the optimal solutions. The step by step solutions of the transportation problems can be obtained by using OTPA [23] or TORA [24] software. Also, we will be applying the proposed technique to obtain multiple optimal solutions where the transportation routes are less than the previous optimal solutions. Earlier, we discussed about the transport risks which are associated with in about all ways of routes. The fewer routes to transport goods minimize the probability of risks to occur any inconvenience situation.
![]()
Table 4. Applying Modified Distribution Method (MODI) for zero opportunity cost.
![]()
Table 5. New optimal solution with seven positive allocations.
![]()
Figure 1. Optimal solution with eight routes, where each route has some common risks to transport goods.
![]()
Figure 2. Optimal solution with seven routes, where there are fewer risks than Figure 1 to transport goods.
![]()
Figure 3. Risk minimization by reducing the transportation routes. (a) Optimal solution with eight routes, where each route has some common risks to transport goods. (b) Optimal solution with seven routes, where there are less risks than (a) to transport goods.
6.1. Example-1
Let us consider a transportation problem (TP) in Table 6 with five sources and five destinations. We solved this problem by finding initial feasible solution by Vogel’s Approximation Method (VAM) and obtained optimal solution by MODI.
The initial feasible solution solved by Vogel’s Approximation Method (VAM) of the above TP is shown in Table 7.
The optimal solution obtained by MODI is given below:
In Table 7, we observed that there are nine optimal routes and also, in (S4, D1) cell the opportunity cost is zero. Then we apply our technique that repeats the step-5 to step-8 of MODI algorithm to obtain another optimal solution which shown in Table 8.
The above optimal solution in Table 9 contains eight optimal routes which is less than the previous optimal
![]()
Table 6. The transportation problem table.
![]()
Table 7. Initial feasible solution of the above transportation problem by Vogel’s Approximation Method (VAM).
![]()
Table 8. Optimal solution by Modified Distribution Method (MODI) with nine positive allocations.
solution. That’s mean the risks associate with all the routes are less than the previous optimal solution.
6.2. Example-2
Let us consider another transportation problem (TP) with four sources and four destinations as shown in Table 10. We solved this problem by finding initial feasible solution by Least Cost Method (LCM) and obtained optimal solution by MODI.
The initial feasible solution solved by Least Cost Method (LCM) of the above TP is shown in Table 11.
The optimal solution obtained by MODI is given below:
In Table 12, we observed that there are seven optimal routes and also, in (S3, D3) and (S4, D3) cells the opportunity costs are zero. Then we apply our technique that repeat the step-5 to step-8 of MODI algorithm to obtain another optimal solution.
The above optimal solution as shown in Table 13 contains six optimal routes which is less than the previous optimal solution. That’s mean the risks associate with all the routes are less than the previous optimal solution.
![]()
Table 9. New optimal solution with eight positive allocations.
![]()
Table 10. The transportation problem table.
![]()
Table 11. Initial feasible solution of the above transportation problem by Least Cost Method (LCM).
![]()
Table 12. Optimal solution by Modified Distribution Method (MODI) with seven positive allocations.
![]()
Table 13. New optimal solution with six positive allocations.
7. Conclusion
The transport risk management system consists of some common risks in about all ways of routes such as highway, waterway, airway, railway and so forth. Those risks may affect the transportation system which can damage goods or delay shipment. In this paper, we developed a technique to obtain multiple optimal solutions using Modified Distribution Method (MODI) of a transportation problem. These multiple optimal solutions provide same optimal transportation costs, but sometimes some of these optimal solutions provide less decision variables or routes than others. In that case, probability of occurring risk factors will be reduced. Using more routes to transport goods increases the probability of occurring risk factors which may hamper the distribution of goods. Finally, we conclude that our proposed technique by MODI method minimizes the transportation routes which minimize the probability of occurring some risk factors in the transportation system.
NOTES
![]()
*Corresponding author.