Non-Negative Matrix Factorization Based UKF Algorithm for Constant Modulus Signals in Adaptive Beamforming ()
1. Introduction
Adaptive blind beamforming plays an important role in the contemporary communication systems where it constantly tributes to the enhancement of the signals that tend to be received or transmitted. Adaptive beamforming is achieved through varying the tap weights assigned to each antenna at every time instant applying signal processing algorithm.
The weights are adjusted such that maximum array sensor gain is obtained with minimal amount of residual error. On processing the beamforming signals, the computational complexity depends on the algorithm which works upon the signals. The recent UKF-CMA algorithm for blind beamforming application works quite well compared to other beamforming techniques such as Least Mean Squared-Constant Modulus Algorithm (LMS-CMA) and Recursive Least Mean Squared-Constant Modulus Algorithm (RLS-CMA) with higher computational complexity [1] .
The UKF-CMA algorithm enabled in Gaussian conditions converges to optimal solution when measurement noise is considered. However, UKF-CMA with process noise results in sub-optimal solution [2] [3] . The CM criterion is incorporated into Weiner filter through which adaptability is achieved [2] . Generally, Constant Modulus (CM) cost functions with quadratic nature are very sensitive to array tap weights and can be minimized using Stochastic Gradient Descent methods (SGD) and the stability of SGD methods relatively depends on the step-size selected and thus results in slow rate of convergence [2] .
An approximation of various CM algorithms is proposed. The computational cost of the Lagrangian formulated beamforming methods is higher over the regularized beamforming methods [4] . In unscented transform, the choice of sigma points is controlled by l, which in turn linearises equal to the second order Gauss filter that results in optimal convergence of the solution [3] [5] . A new discriminant based non-negative matrix factorization algorithm is proposed for facial image characterization problems where discriminant analysis is based on the classification features [6] .
A variant of NMF algorithm is proposed for blind source separation where it is a promising solution for spectral unmixing in hyper-spectral image processing and feature extraction [7] . Different methods of initialization are studied for NMF algorithm, where initialization plays an important role since decomposition is non-convex with many local minima [8] .
Non-Negative Matrix Factorization Algorithm
Non-Negative Matrix Factorization (NMF), a relatively novel technique for dimen- sionality reduction, has been in the growing fast since its origin. It incorporates the non-negativity constraint and thus achieves the parts-based representation as well as enhancing the construe of the problem correspondingly [9] [10] . Some new algorithms for NMF are proposed for blind source separation application when sources are statistically dependent by imposing constraints to the matrix [11] . Multichannel NMF decomposition algorithms are proposed for blind audio source separation. More variants of NMF algorithms for blind sources separation techniques can be found in [12] - [14] . An extensive survey of NMF algorithms can be seen in [15] . In rectangular matrix, the solution is normally iterative and the steps normally require a
. In NMF, we make sure that the complexity is reduced to
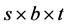, where t is the rank of the matrix. This is achieved by factoring the matrix, as a product of 2 matrices, where first matrix acts as a set of basis vectors and other is positive definite. In quadratic problems, the coefficient matrix has to be positive-definite which
is not true in general case, NMF forces the coefficient matrix to be positive-definite that results in closed-form solution.
Figure 1 describes about the flow of the algorithm.
The algorithm can be given as,
Initialize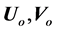 
and 
for
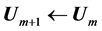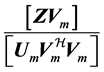
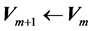o 
o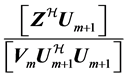 
![]()
end
Where
, 
, 
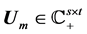are non-negative matrices and the reduced rank t is given by 
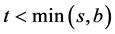where
.
In this paper, we have reduced the computational complexity of UKF-CMA algorithm by reducing dimensionality of the matrix computation, which is achieved through the non-negative matrix factorization.
Note: Notations followed in the paper are bold small letters are vector. Capital letters are matrix.
2. Beamforming Model
Consider a linear array of size L of uniform spacing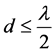 
and n is the number ofsource signals (interference and desired signals). The signal output of an adaptive beamformer is represented as [1] ,
![]()
Figure 1. Flowchart of NMF-UKF-CMA algorithm.
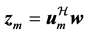(1)
The input signal vector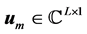 
as,
![]()
(2)
where![]()
, ![]()
is the source signal vector whose first ele- ment is desired signal and remaining elements of the vector are made as interference signals, ![]()
is circular complex Gaussian noise at m-th time instant.
The spatial signature matrix![]()
, Where![]()
,
![]()
, ![]()
, ![]()
is the array phase function, ![]()
is the phase constant, d is the array spacing, ![]()
is ![]()
element of the AOA vector![]()
.
The Constant Modulus (CM) cost function for adaptive beamforming problem can be formulated as
![]()
(3)
where![]()
, ![]()
and ![]()
is the signal modulus of the desired signal![]()
, which is a known a priori. As stated, the optimization problem is non-convex and non-linear.
3. Algorithm Formulation
The constant modulus criterion in (3) assumes that the unknown system model ![]()
for the input signal ![]()
is equal to the constant modulus of the desired signal ![]()
in (5).
![]()
(4)
![]()
(5)
The final state space model is obtained by incorporating process noise![]()
. Since initial received signal is unknown, so we take it as noise ![]()
adding to the model in (7). Applying the non-linearity ![]()
in (8).
![]()
(6)
![]()
(7)
![]()
(8)
![]()
where ![]()
and ![]()
is the process noise.
In (10) ![]()
is approximated by non-negative matrix factorization.
![]()
(9)
![]()
(10)
where![]()
, ![]()
, ![]()
are non-negative matrices and the reduced rank t is given by ![]()
where![]()
. In the algorithm formulation, we ignore the process noise ![]()
on including leads to suboptimal solution.
4. Proposed NMF-UKF-CMA Algorithm
The proposed NMF-UKF-CMA algorithm is as follows,
Input:![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
Initialize: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
then initialize the unscented Kalman filter with
![]()
of size![]()
,
for ![]()
do
Compute and update
・ Extract the sigma points ![]()
as
![]()
(11)
where ![]()
is an initial weight vector.
・ Extract matrix ![]()
for the input signal ![]()
as
![]()
and then get the sigma points ![]()
for the updated state as
![]()
(12)
where![]()
.
・ Extract the posteriori estimate ![]()
as
![]()
(13)
where j denotes the j-th column vector for ![]()
and j―the element for vector![]()
.
・ Extract the sigma priori covariance ![]()
as
![]()
(14)
where j is the j-th column vector for ![]()
and j-th element for vector![]()
.
・ Extract the sigma points ![]()
through non-linear function as
![]()
(15)
where ![]()
for each element of the j-th column vector for ![]()
for![]()
.
・ The output sigma points are approximated using non-negative matrix factorization algorithm as ![]()
![]()
(16)
where![]()
, ![]()
are non-negative matrices and reduced rank![]()
.
・ Applying the output sigma points to extract the estimated output ![]()
as
![]()
(17)
・ The obtained crosscovariance matrix ![]()
as
![]()
(18)
・ The obtained autocovariance ![]()
as
![]()
(19)
where ![]()
・ Now apply the Kalman innovation matrix and the update formulas as
![]()
(20)
![]()
(21)
![]()
(22)
・ Update the optimal weight vector![]()
. end
5. Simulation and Results
In this section, the performance of NMF-UKF-CMA algorithm is compared with existing UKF-CMA algorithm. An uniform linear array of length L = 20 and of spacing ![]()
for simulation. The constant modulus signals are generated by Minimum Shift Keying (MSK) Modulation scheme with unity modulus and the interference plus noise signal were set as Gaussian distributed random variables with mean, 0 and noise variance of 1. An uniform distribution of ![]()
to ![]()
is followed for phase. The desired direction of arrival is set as 10˚ and for interference signals are set as 25˚, −30˚ and −45˚. The CMA criterion is chosen as p = 1 and q = 2 in the simulations, for which we achieve optimal signal-to-interference-plus-noise ratio (SINR). In addition to SINR in dB, Mean Square Deviation (dB) and Array Sensor Gain (dB) are the parameters, also used to estimate the performance of the array algorithms. MSD is defined as![]()
. The value of ![]()
is set as 0.75 in all the simulations. The plots simulated are stochastic averages of 500 independent simulations.
Simulation-1
In Simulation-1, The interference plus noise signal of variance (![]()
) is set as 0.1. From Figure 2, NMF-UKF-CMA algorithm has improved gain and grating lobe suppression compared to UKF-CMA. Lesser mean square deviation for NMF-UKF-
![]()
Figure 2. Simulation 1: SINR in dB (left), Array Sensor Gain in dB (center), MSD in dB (right) with![]()
.
CMA for the given noise variance to the UKF-CMA. The proposed NMF-UKF-CMA algorithm attains much better SINR compared with UKF-CMA as the sample size increases. The convergence of NMF-UKF-CMA algorithm gives better attenuation of interferences compared to UKF-CMA and it converges within the limited sample space.
Simulation-2
In Simulation-2,The interference plus noise signal of variance (![]()
) is set as 0.0316. From Figure 3, We achieve similar results compared to UKF-CMA as the noise variance decreases. We could observe betterment of proposed algorithm MSD com- pared to UKF-CMA. The SINR values of NMF-UKF-CMA algorithm closely follow the UKF-CMA algorithm.
Simulation-3
In Simulation-3, The number of antennas L in the array is increased to 60 and remaining parameters are set as in simulation 1. From Figure 4, we achieve an in- creased SINR for NMF-UKF-CMA algorithm as the number of antenna is increased.
Simulation-4
In Simulation-4, The number of sources M is increased to 7, interference’s added in the direction of 35˚, 55˚, −55˚ and the number of antennas L is decreased to 4 and p is set as 0.5 for the simulation are performed. From Figure 5, As seen, there is de- gradation in SINR as the number of sources increased. The similarity in performance can be seen for NMF-UKF-CMA and UKF-CMA as the number of sources increased.
6. Conclusion
A technique for dimensionality reduction and compression of cross-covariance matrix is achieved through NMF Algorithm, found to be more effective in beamforming. NMF achieves superiority over the classic low rank reduction algorithms such as PCA and LDA by imposing purely additive constraint or positivity criteria on the matrix. The initialization and the determination of number of basis vectors add to faster con- vergence of the solution. By incorporating the technique in to a adaptive blind beamforming problem, our proposed NMF-UKF-CMA algorithm has better performance compared to UKF-CMA algorithm. On close observation, as the number of antennas in the array and noise variance increases, we achieve better Sensor Array Gain, Signal
![]()
Figure 3. Simulation 2: SINR in dB (left), Array Sensor Gain in dB (center), MSD in dB (right) with![]()
.
to Interference plus Noise Ratio and Mean Squared Deviation with reduced computational complexity.