Joule-Lenz Energy of Quantum Electron Transitions Compared with the Electromagnetic Emission of Energy ()
Received 4 July 2016; accepted 19 August 2016; published 22 August 2016

1. Introduction
Usually any calculation of the emission rate of energy in the atom has as its background a rather complicated statistical-and-probabilistic theory. This situation seems to be not changed much since the very end of the nineteenth and beginning of twenteeth century [1] - [3] . In practice an individual atomic system has been never considered, but instead of it an ensemble of the oscillating atoms known as the black body was examined. Rather automatically the temperature parameter―important for comparing the theoretical results with experiment―has been involved in such many-atomic calculations. Next the probabilistic approach to the emission intensity found its justification, and a rather extended though complicated application, in quantum mechanics [4] [5] .
More recently an approach to the treatment of the energy emission in a single atomic object could be based on the Joule-Lenz law [6] - [10] . For, when the Bohr theory of the hydrogen atom is taken as an example, any atom has its electron placed on a definite orbit which can be approximated by a circle. Electrically such a circular motion can be represented by a current having a known intensity. For example, for the quantum states n and 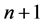 the current intensity is respectively
the current intensity is respectively
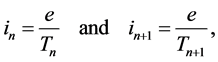 (1)
(1)
where 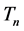 and
and 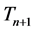 are the time periods of the electron circulation about the proton nucleus. In the next step, the energy difference between levels
are the time periods of the electron circulation about the proton nucleus. In the next step, the energy difference between levels 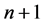 and n, namely
and n, namely
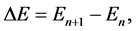 (2)
(2)
provides us with the electric potential
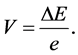 (3)
(3)
This leads to the electric resistance
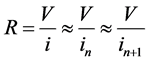 (4)
(4)
where the approximate relations in (4) hold in virtue of
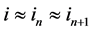 (5)
(5)
valid for large n. The validity of (5) becomes evident if we apply Formula (7) in (1).
For such large n we have [11] the energy change
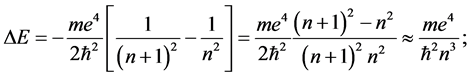 (6)
(6)
in the last step of (6) the approximation of large n is considered.
Since [11]
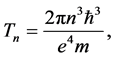 (7)
(7)
we obtain
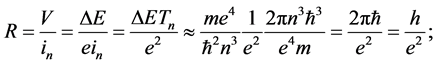 (8)
(8)
this is a constant independent of n. The same value of R can be calculated also for other quantum systems than the hydrogen atom, see [6] [7] [10] . A characteristic point is that R is equal to a well-known result of ex- periments done on the integer quantum Hall effect [12] .
The Joule-Lenz law is represented by the well-known relation
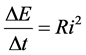 (9)
(9)
where 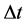 is the time interval necessary to produce the emitted energy
is the time interval necessary to produce the emitted energy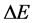 . In fact (9) implies that for
. In fact (9) implies that for ![]() we have
we have
![]() (10)
(10)
Moreover from (6) and (10) we obtain
![]() (11)
(11)
or
![]() (12)
(12)
Therefore the ratio (9) becomes
![]() (13)
(13)
Results similar to (10)-(12) can be obtained also for other quantum systems than the hydrogen atom [6] [7] [10] .
The principal aim of the paper is, in the first step, to compare the ratio calculated in (13) with the rate of energy emission obtained in terms of the electromagnetic theory. Next, in order to compare the quantum emission with the classical emission rate, the properties of the harmonic oscillator emission are also studied.
2. Fields Induced by the Electron Motion in the Hydrogen Atom
The electric field value ![]() acting on the electron in the Bohr atom is well known:
acting on the electron in the Bohr atom is well known:
![]() (14)
(14)
The last step in (14) is attained because of the radius of the orbit n which is [11]
![]() (15)
(15)
A less-known magnetic field omitted in the Bohr atomic model [10] is induced in the hydrogen atom due to the circular electron motion done with the frequency
![]() (16)
(16)
Because of the formula (see e.g. [13] )
![]() (17)
(17)
the identity between (16) and (17) combined with (7) gives
![]() (18)
(18)
A characteristic point is that when expressions for ![]() and
and ![]() are substituted to the Lorentz force
are substituted to the Lorentz force
![]() (19)
(19)
we obtain for the electric component of (19)
![]() (20)
(20)
and the same value is obtained for the magnetic component of (19)
![]() (21)
(21)
on condition the vector of the electron velocity having the value [11]
![]() (22)
(22)
is normal to![]() .
.
3. Field Values Specific for the One-Electron Current Present in the Atom and the Electromagnetic Rate of the Energy Emission
Our aim is to construct the Poynting vector which provides us with the electromagnetic dispense of energy. The vectors ![]() and
and ![]() become slightly diffferent than in Section 2 because they refer to the current behaviour of the electron which is circulating along its orbit. With the potential V given in (3) and (6) and equal to
become slightly diffferent than in Section 2 because they refer to the current behaviour of the electron which is circulating along its orbit. With the potential V given in (3) and (6) and equal to
![]() (23)
(23)
the electric field on the orbit having the length
![]() (24)
(24)
attains the value [16]
![]() (25)
(25)
This gives an electric vector directed along the current.
On the other hand the magnetic field directed normally to the current attains the value [14] [16]
![]() (26)
(26)
This field differs from that given in (18) solely by the factor equal to![]() .
.
It should be noted that parameter ![]() entering (26) is the radius of the circular cross-section area of the orbit assumed to be equal to the cross-section of the electron microparticle considered as a sphere [15] [17] :
entering (26) is the radius of the circular cross-section area of the orbit assumed to be equal to the cross-section of the electron microparticle considered as a sphere [15] [17] :
![]() (27)
(27)
The value of the Poynting vector emanating the energy from the orbit is calculated according to the formula [14]
![]() (28)
(28)
where
![]() (29)
(29)
is the toroidal surface of the orbit having the length (24) and the length of the cross-section circumference of the orbit is equal to
![]() (30)
(30)
In effect we obtain from (23), (26) and (28) the result precisely equal to Formula (13) calculated from the Joule-Lenz theory. Since (13) assumed the electron transitions solely between the levels
![]() (31)
(31)
the identity between (13) and (28) implies that the limitation to transition (31) applies also to the electro- magnetic result calculated in (28).
A problem may arise to what extent the energy rate (13), or (28), can be radiated as an electromagnetic wave. An altenative behaviour is that the energy ![]() is spent for a mechanical rearrangement of the electron position due to the transition process. An argument for that is the presence of the electric force
is spent for a mechanical rearrangement of the electron position due to the transition process. An argument for that is the presence of the electric force
![]() (32)
(32)
along the orbit. The force (32) multiplied by the orbit length calculated in (24) gives
![]() (33)
(33)
which is precisely the energy ![]() of the electron transition obtained in (6).
of the electron transition obtained in (6).
4. Quantum and Classical Emission Rate Calculated for the Harmonic Oscillator
A natural tendency is to compare the quantum rate of the energy emission with the classical emission rate. To this purpose the one-dimensional harmonic oscillator has been chosen as a suitable object of examination.
The classical energy of the oscillator is
![]() (34)
(34)
a is the oscillator amplitude; m is the oscillator mass which together with the force constant k refers to the circular frequency of the oscillator
![]() (35)
(35)
T is the oscillation period [18] .
The quantum oscillator energy is
![]() (36)
(36)
(the last step holds for large n) and the change of energy due to transition between the levels ![]() and n is
and n is
![]() (37)
(37)
According to the Joule-Lenz approach to the quanta [6] - [10] the emission rate between the levels ![]() and n is
and n is
![]() (38)
(38)
This gives
![]() (39)
(39)
so
![]() (40)
(40)
because the reference between ![]() and
and ![]() is
is
![]() (41)
(41)
The potential V connected with the energy change ![]() is
is
![]() (42)
(42)
If we note that a maximal distance travelled by the electron oscillator in one direction is
![]() (43)
(43)
the electric field connected with the oscillator parallel to its motion is
![]() (44)
(44)
The electric current let be considered as remaining approximately constant in course of the oscillation. In this case the magnetic field which is normal to the current [see (26)] is
![]() (45)
(45)
since the cross-section of the electron current is assumed to be identical with the cross-section area of the electron microparticle, see (27).
The surface area of the sample containing the oscillator is
![]() (46)
(46)
on condition the contribution of the end areas of the sample surface equal to
![]() (47)
(47)
has been neglected because (47) is a small number in comparison with S in (46).
In consequence, for the vector ![]() normal to vector
normal to vector ![]() the value of the Poynting vector becomes
the value of the Poynting vector becomes
![]() (48)
(48)
This is a result identical with (38) on condition Formula (39) is taken into account.
According to the classical electrodynamics [19] the emission rate of energy from a classical oscillator is
![]() (49)
(49)
since
![]() (50)
(50)
is the dipole moment of the classical harmonic oscillator. Formula (49) can be compared with the quantum approach to the Joule-Lenz emission rate of energy [see (38)]:
![]() (51)
(51)
In the case of very small quantum systems the amplitude a in (49) can be close to its minimal length [10]
![]() (52)
(52)
and the time period T can approach its minimal size [10]
![]() (53)
(53)
The equality required between (49) and (51) leads to the relation
![]() (54)
(54)
When a and T are taken respectively from (52) and (53), Formula (54) becomes
![]() (55)
(55)
from which we have the relation
![]() (56)
(56)
The result obtained in (56) differs by only 20 percent from the reciprocal value of the atomic constant equal to 137.
5. Ratio of the Classical and Quantum Emission Rate Defined by the Damping Coefficient of the Classical Radiation
An attempt of this Section is to demonstrate that the classical emission can be considered as a damped quantum emission rate. The classical damping coefficient of the oscillator is [19]
![]() (57)
(57)
On the other hand, the classical emission rate given in (49) can be modified when the amplitude a entering (49) is expressed in terms of the oscillator energy E [18] :
![]() (58)
(58)
Here, at the end of (58), the energy E is replaced by the approximate quantum formula for the oscillator energy given in (36). In effect the classical emission rate in (49) becomes
![]() (59)
(59)
Another transformation may concern the quantum emission rate in (51):
![]() (60)
(60)
As a result of (59) and (60) we obtain the ratio
![]() (61)
(61)
which is proportional to ![]() in (57). A multiple of the oscillation time period T is the proportionality coefficient representing (61) in terms of
in (57). A multiple of the oscillation time period T is the proportionality coefficient representing (61) in terms of![]() . Therefore another way to write (61) can be
. Therefore another way to write (61) can be
![]() (62)
(62)
Let us note that ![]() entering (36) and (58) is proportional to n.
entering (36) and (58) is proportional to n.
It is worth to note that the Einstein coefficient ![]() of the emission probability can be coupled with
of the emission probability can be coupled with ![]() by the relation [20]
by the relation [20]
![]() (63)
(63)
so
![]() (64)
(64)
According to Heisenberg [20] [21] we have
![]() (65)
(65)
where a is the quantum-theoretical amplitude of the expansion of the coordinate ![]() of an anharmonic oscillator;
of an anharmonic oscillator; ![]() is the circular frequency of the harmonic oscillator.
is the circular frequency of the harmonic oscillator.
For small peturbation ![]() of the oscillator we have [21]
of the oscillator we have [21]
![]() (66)
(66)
so Formula (65) gives
![]() (67)
(67)
or
![]() (68)
(68)
In effect for ![]() taken in (63) we obtain from (64) and (68):
taken in (63) we obtain from (64) and (68):
![]() (69)
(69)
If ![]() is presented, according to (61), in terms of the ratio of
is presented, according to (61), in terms of the ratio of ![]() and
and![]() , we obtain
, we obtain
![]() (70)
(70)
where T is the oscillation time period of the harmonic oscillator.
6. Reciprocal Value of the Atomic Constant and the Electron Spin
The reciprocal value ![]() of the atomic constant (~137) approached in (56) is important in the treatment of the electron spin [10] [22] [23] . We show below that the magnetic field intensity necessary to produce the electron spin can be obtained approximately as a result of a coupling of
of the atomic constant (~137) approached in (56) is important in the treatment of the electron spin [10] [22] [23] . We show below that the magnetic field intensity necessary to produce the electron spin can be obtained approximately as a result of a coupling of ![]() with the radius
with the radius ![]() of the electron microparticle, see (27).
of the electron microparticle, see (27).
According to the classical electrodynamics [14] the magnetic field H at a distant r from the center of the linear wire carrying a current i is coupled with i and r by the formula
![]() (71)
(71)
If the current i is flowing on a surface of the conductor which is the electron orbit, we can assume that ![]() which is both the radius of the electron microparticle and cross-section of the orbit. The field H becomes in this case [14]
which is both the radius of the electron microparticle and cross-section of the orbit. The field H becomes in this case [14]
![]() (72)
(72)
where the time period T of the electron circulation along the orbit is taken from Formula (7) for![]() :
:
![]() (73)
(73)
The essence of the spin effect is that the path of the spinning electron circumvents the electron orbit about
![]() (74)
(74)
times during the time period T indicated in (73). In classical electrodynamics this means that the magnetic field produced in this way is ![]() times stronger than that obtained in (72):
times stronger than that obtained in (72):
![]() (75)
(75)
The result in (75) differs solely by the factor of ![]() from the magnetic field assumed to produce a spinning
from the magnetic field assumed to produce a spinning
electron particle in [10] [22] [23] :
![]() (76)
(76)
A discrepancy between (75) and (76) can be ascribed to some uncertainty connected with the calculation of the radius![]() , see [24] .
, see [24] .
7. Conclusions
The aim of the paper was to get more insight into a non-probabilistic description of the transfer of energy between two quantum levels. A suitable situation for discussion is the case when the levels are neighbouring in their mutual position of the energy states. Then the energy change (![]() ) between the levels, and the time interval
) between the levels, and the time interval ![]() necessary to attain
necessary to attain![]() , satisfy a very simple formula
, satisfy a very simple formula
![]() (77)
(77)
see [6] -[10].
In the paper, Formula (77) finds its counterparts supplied by the electromagnetic theory of emission. Two physical objects, namely the hydrogen atom and electron harmonic oscillator, were studied. The case of the electron oscillator allowed us to perform a more direct comparison of the quantum approach to the emission rate with the classical electromagnetic theory. It occurs that the classical rate is equal to the quantum rate multiplied by the Born damping coefficient and an interval of time, see (62).