Received 18 June 2016; accepted 8 August 2016; published 11 August 2016

1. Introduction
For a given function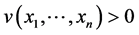 , defined in a domain
, defined in a domain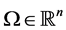 , let us calculate its partial derivatives in the logarithmic space:
, let us calculate its partial derivatives in the logarithmic space:
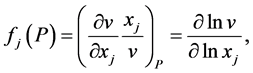 (1)
(1)
where 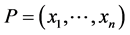 is an arbitrary point. If
is an arbitrary point. If 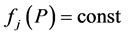 in the domain
in the domain 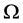 for all j, then v clearly is a
for all j, then v clearly is a
power function in 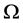 of the form
of the form 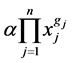 where
where . In this paper we study piecewise constant ap-
. In this paper we study piecewise constant ap-
proximations of the quantities (1) or, in other words, nonlinear approximations of the function v by piecewise power functions.
This study is first of all motivated by applications in Systems Biology, where many networks can be de- scribed via compartment models
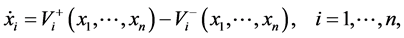 (2)
(2)
with the influx and efflux functions 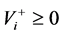 and
and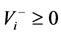 , respectively.
, respectively.
For instance, in a typical metabolic network used in Biochemical Systems Theory the index 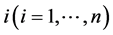 refers to the n internal metabolites
refers to the n internal metabolites . The influx
. The influx , resp. efflux
, resp. efflux ![]() function accounts for the rate (velocity) of a production (synthesis), resp. degradation of the metabolite
function accounts for the rate (velocity) of a production (synthesis), resp. degradation of the metabolite![]() .
.
Another important example is gene regulatory networks which in many cases can be described as a system of nonlinear ordinary differential equations of the form
![]() (3)
(3)
where ![]() is the gene concentration (i = 1, ・・・, n) at time t, while the regulatory functions
is the gene concentration (i = 1, ・・・, n) at time t, while the regulatory functions ![]() and
and ![]() depend on the response functions
depend on the response functions![]() , which control the activity of gene k and which are assumed to be sigmoid-type functions [1] .
, which control the activity of gene k and which are assumed to be sigmoid-type functions [1] .
The derivatives ![]() in the logarithmic space are very important local characteristics of biological net- works. In Biochemical Systems Theory these derivatives are known as the kinetic orders of the function v, while in Metabolic Control Analysis (see e.g. [2] ) they are called elasticities. From the mathematical point of view, these quantities measure the local response of the function v to changes in the dependent variable (for instance, the local response of enzyme or other chemical reaction to changes in its environment). Thus, they describe local sensitivity of the function v, the terminology which is widespread in e.g. engineering sciences.
in the logarithmic space are very important local characteristics of biological net- works. In Biochemical Systems Theory these derivatives are known as the kinetic orders of the function v, while in Metabolic Control Analysis (see e.g. [2] ) they are called elasticities. From the mathematical point of view, these quantities measure the local response of the function v to changes in the dependent variable (for instance, the local response of enzyme or other chemical reaction to changes in its environment). Thus, they describe local sensitivity of the function v, the terminology which is widespread in e.g. engineering sciences.
If all influx and efflux functions in (2) have constant kinetic orders, one obtains the so-called “synergetic system”, or briefly “S-system”:
![]() (4)
(4)
where the exponents![]() ,
, ![]() represent all the (constant) kinetic orders associated with (4). The right-hand side of an S-system, thus, contains power functions, and analysis based on S-systems is, therefore, called “Power- Law (PL) Formalism”, see e.g. [3] - [7] ).
represent all the (constant) kinetic orders associated with (4). The right-hand side of an S-system, thus, contains power functions, and analysis based on S-systems is, therefore, called “Power- Law (PL) Formalism”, see e.g. [3] - [7] ).
The Power-Law Formalism has been successfully applied to a wide number of problems, for example, to metabolic systems [8] , gene circuits [9] , signalling networks [10] . Such systems are very advantageous in bio- logical applications, as the systems’ format considerably simplifies mathematical and numerical analysis such as steady state analysis, sensitivity, stability analysis, etc. For instance, calculation of steady states for the S- systems is a linear problem (see [7] ). By these and other biological and mathematical reasons, it was suggested in [11] to classify such systems as “a canonical nonlinear form” in systems biology.
In many models, however, the kinetic orders may vary considerably. A typical example is a model coming from Generalized Mass Action
![]() (5)
(5)
where the power functions ![]() describe the rates of the process no. r, while
describe the rates of the process no. r, while ![]() is a stoichiometric factor that stands for the number of molecules of
is a stoichiometric factor that stands for the number of molecules of ![]() produced, i.e.
produced, i.e. ![]() or
or![]() . Collect- ing the processes in (5) in a net process of synthesis
. Collect- ing the processes in (5) in a net process of synthesis ![]() (positive terms) and a net process of degradation
(positive terms) and a net process of degradation ![]() (negative terms) results in an aggregated system (2), which is not an S-system.
(negative terms) results in an aggregated system (2), which is not an S-system.
Another example of generic systems with non-constant kinetic orders stems from Saturable and Cooperativity Formalism [12] reflecting two essential features of biological systems, which gave the name to this formalism (see [13] for more details). In this case, the system (5) becomes
![]() (6)
(6)
where ![]() and
and![]() ,
, ![]() ,
, ![]() and
and ![]() are real numbers.
are real numbers.
Another version of Saturable and Cooperativity Formalism, which is mentioned in [12] , is defined as follows:
![]() (7)
(7)
where ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are real numbers.
are real numbers.
In the case of gene regulatory networks (3) the sensitivities (1) are non-constant as well, even if one considers the functions ![]() and
and ![]() to be multilinear in
to be multilinear in![]() . In addition, the usage of non-multilinear functions are also known in this theory [14] .
. In addition, the usage of non-multilinear functions are also known in this theory [14] .
Taking into account the importance of kinetic orders/elasticities/sensitivities (1) in Systems Biology, one one hand, and convenience of the well-developed analysis of S-systems (stability theory [7] , parameter estimation routines [15] , software packages) on the other, a new kind of generic representations of compartment systems (2) was suggested in [16] (see also [17] for further applications of this representation). According to this idea, the entire operating domain is divided to partition subsets where all kinetic orders can be viewed as constants. In other words, the system (2) is approximated by a set of S -systems, each being only active in its own partition subset. This way of representing (2) is called “Piecewise Power-Law Formalism” [18] .
From the biological point of view, piecewise power-law representations are useful in many respects, when compared to other ways of approximations, as they take into account biologically relevant characteristics (kinetic orders) rather than the standard partial derivatives. Therefore, piecewise S-systems preserve important biological structures and, at the same time, do not destroy a relatively simple mathematical structure of plain S-systems. By this reason, approximations of a general target function by piecewise power approximations may be of a great importance for biological and other modelling. A rigorous mathematical justification of the idea of piecewise power-law approximations is the main purpose of the present paper. More precisely, we consider mean-square and uniform convergence of approximations by piecewise power functions to the target function provided that the associated partitions of the operating domain ![]() satisfy some additional assumptions. One of the challenges is that partitions of the operating domain
satisfy some additional assumptions. One of the challenges is that partitions of the operating domain ![]() may not be chosen freely in applications. For instance, the partitions may directly stem from biological properties of the model [17] . Other ways of con- structing partitions can be dictated by optimality-oriented algorithms. In Appendix (see also [18] ) we describe such a method which goes back to the paper [19] and which is based on an automatical procedure, allowing to obtain simultaneously the best possible polyhedral partition and the respective best possible piecewise linear approximation in the logarithmic space.
may not be chosen freely in applications. For instance, the partitions may directly stem from biological properties of the model [17] . Other ways of con- structing partitions can be dictated by optimality-oriented algorithms. In Appendix (see also [18] ) we describe such a method which goes back to the paper [19] and which is based on an automatical procedure, allowing to obtain simultaneously the best possible polyhedral partition and the respective best possible piecewise linear approximation in the logarithmic space.
The main results of the paper are presented in Section 3 (mean-square convergence of piecewise power approximations) and in Section 4 (uniform convergence of piecewise power approximations). Several auxiliary results are proved in Appendices A.1-A.3, while Appendix A.4 presents an approximation algorithm which provides an automated partition and the respective best possible approximation in the logarithmic space for a given number of subdomains. Finally, in Appendix A.5 we explane by example why a direct piecewise power- law fitting is ill-posed.
2. Preliminaries
Throughout the paper we use the following notations (see Table 1). Let ![]() and let
and let ![]() be given by
be given by ![]()
![]()
Let ![]() be a domain in the space
be a domain in the space ![]() which we call Cartesian. We assume
which we call Cartesian. We assume ![]() to be closed and
to be closed and
bounded (i.e. compact) subset of![]() . Let
. Let ![]() be its image in the logarithmic space
be its image in the logarithmic space ![]() and
and ![]() be a
be a
measurable partition of![]() . This means that
. This means that ![]() are all Borel measurable subsets of
are all Borel measurable subsets of![]() ,
, ![]() for
for
every ![]() and
and ![]() for any natural N. In some results and algorithms
for any natural N. In some results and algorithms ![]() will be a poly-
will be a poly-
hedron domain in the logarithmic space, and ![]() will be a polyhedral partition.
will be a polyhedral partition.
Below ![]() is the measurable partition of
is the measurable partition of ![]() which is the image of the partition
which is the image of the partition ![]() under the
under the
inverse logarithmic transformation.
![]()
Table 1. Overview of the basic terminology and notation used in the paper (LS-least-squares).
We also put ![]()
Let ![]() be a least-squares (LS) power-law fitting to the function v on
be a least-squares (LS) power-law fitting to the function v on![]() ,
,![]() For
For
![]() we consider the piecewise power function
we consider the piecewise power function ![]() whenever
whenever ![]() We put
We put ![]()
Let ![]() be a LS linear approximation to the function
be a LS linear approximation to the function ![]() on
on ![]()
![]() For
For
![]() we consider the piecewise linear function
we consider the piecewise linear function ![]() whenever
whenever ![]() We put also
We put also ![]()
We remind that the parameters ![]() and
and ![]() of the linear functions
of the linear functions ![]() are uniquely obtained from the following minimization criterion in the logarithmic space:
are uniquely obtained from the following minimization criterion in the logarithmic space:
![]() (8)
(8)
Alternatively, one can define approximations of the target function v by power functions minimizing the distance in the space![]() :
:
![]() (9)
(9)
Our last minimization criterion looks similar to (6), but is, in fact, very different
![]() (10)
(10)
as the minimum here is taken over all polyhedral partitions ![]() of the polyhedral domain
of the polyhedral domain![]() , and all
, and all
corresponding linear functions ![]() (
(![]() ).
).
The main advantage of the criteria (8) and (10) is their linearity that provides the uniqueness of the solution and also makes the process of finding the solution computationally cheap, as it is based on explicit matrix formulas. On the other hand the use of the logarithmic transformation requires caution. The influences of the data values will change, as will the error structure of the model. Yet, the criterion (8) only requires a standard linear regression, while the criterion (10) requires a special regression algorithm, still linear, but much more involved (see Appendix A.4 for details).
The criterion (9) gives best possible approximation in terms of the LS error in the Cartesian space. However, a nonlinear regression algorithm should be used in this case, which is less advantageous, especially when the number of the estimated parameters is big. In addition, the nonlinear regression may have other drawbacks, one of which is ill-posedness (see Appendix A.5).
3. Mean-Square Convergence of Piecewise Power Approximations
The results of this section provide the mean-square convergence (L2-convergence) of piecewise approximations by power functions. The involved parameters may be e.g. obtained according to one of the minimization criteria (8) or (9).
The main technical challenges stemming from the nature of these minimization algorithms can be sum- marized as follows: 1) the L2-convergence of the approximations in the logarithmic space may not imply the L2-convergence of their images in the Cartesian space (and vice versa); 2) it is not evident that automatic dissections of the operating domain, as e.g. in the algorithms based on the minimization criterion (10), make the diameters of the partition subsets go to zero even if the number of partition subsets tends to ¥.
Three propositions below deal with L2-convergence in the logarithmic domain.
Proposition 1. Let the target function ![]() be measurable and bounded on
be measurable and bounded on ![]() and
and![]() . Suppose
. Suppose
that the measurable partitions ![]() satisfy the property
satisfy the property ![]() (
(![]() ). Then for the corresponding
). Then for the corresponding
LS approximations ![]() in
in ![]() and
and ![]() in
in ![]() we have
we have![]() ,
, ![]() in the respective L2-norms, if
in the respective L2-norms, if![]() .
.
To prove this proposition we need the following lemma, the proof of which can be found in Appendix A.1:
Lemma 1. Let v be measurable and ![]() on
on ![]() for some constants
for some constants![]() . Let
. Let ![]()
and the measurable partitions ![]() satisfy the property
satisfy the property ![]() (
(![]() ). Then there exists a sequence
). Then there exists a sequence
![]() of continuous on
of continuous on ![]() functions satisfying the properties
functions satisfying the properties ![]() on any
on any![]() ,
, ![]()
for all ![]() and
and ![]() (resp.
(resp.![]() ) L2-converges to
) L2-converges to ![]() (resp. v) on
(resp. v) on ![]() (resp.
(resp.![]() ).
).
Proof of Proposition 1. We use the sequences
![]()
from the lemma 1, which both converge in the L2-sense in the respective domains.
Since ![]() is the LS piecewise linear approximation in
is the LS piecewise linear approximation in![]() , we have
, we have
![]()
as![]() . ,
. ,
In the next proposition we do not assume that![]() .
.
Proposition 2. Let ![]() be a polyhedral domain in
be a polyhedral domain in![]() , the function
, the function ![]() be square integrable in
be square integrable in ![]() and
and
![]() be the optimal polyhedral partition of
be the optimal polyhedral partition of ![]() obtained by the algorithm described in Appendix A.4. Then
obtained by the algorithm described in Appendix A.4. Then
for the corresponding LS approximations ![]() in
in ![]() we have
we have ![]() in the L2-norm, if
in the L2-norm, if![]() .
.
Proof. Evidently, for the L2-function ![]() there exists a sequence of polyhedral partitions
there exists a sequence of polyhedral partitions ![]() of
of ![]() such
such
that ![]() as
as ![]() and a sequence of piecewise constant functions
and a sequence of piecewise constant functions ![]() given
given
by ![]() whenever
whenever ![]() for which
for which ![]() in the L2-norm if
in the L2-norm if![]() .
.
For the optimal polyhedral approximation ![]() we obtain
we obtain
![]()
as![]() . ,
. ,
In particular, the assumption on ![]() is fulfilled if the target function v is measurable and bounded on
is fulfilled if the target function v is measurable and bounded on![]() .
.
The case of the L2-convergence of the approximations![]() , given as
, given as![]() , is more involved. The reason for that is that the L2-convergence of the sequence
, is more involved. The reason for that is that the L2-convergence of the sequence ![]() does not necessarily imply the L2-
does not necessarily imply the L2-
convergence of the sequence![]() .
.
We introduce the following notation. Given a partition subset ![]() of
of ![]() we put
we put
![]() (11)
(11)
where the point ![]() is the center of mass of the convex set
is the center of mass of the convex set ![]() given by
given by
![]() (12)
(12)
Let ![]() be the symmetric
be the symmetric ![]() -matrix with the entries defined as
-matrix with the entries defined as
![]() (13)
(13)
Below we fix a matrix norm![]() . All matrix norms are equivalent. One of the norms is Euclidean, which is
. All matrix norms are equivalent. One of the norms is Euclidean, which is
defined via the maximal eigenvalues:![]() . In the case of symmetric, positive definite matrices
. In the case of symmetric, positive definite matrices
(like ![]() above) we can write that
above) we can write that![]() .
.
We say that the sequence of partitions ![]() (
(![]() ) of
) of ![]() satisfies the condition (
satisfies the condition (![]() ) if there exists
) if there exists
a constant ![]() such that
such that
![]()
If the chosen norm is Euclidean, then the latter estimate can be rewritten as
![]()
where ![]() is the least (positive) eigenvalue of the matrix
is the least (positive) eigenvalue of the matrix ![]() (
(![]() ;
;![]() ).
).
Informally speaking, this property means that the partition subsets cannot be too different from each other in the shape. Assume, for instance, that the partition sets are enclosed in rectangular boxes. The result below says that if the ratio of the longest and the shortest edges of the boxes is bounded above, i.e. boxes are not “too thin”, then the sequence of such boxes satisfies the property (![]() ).
).
Proposition 3. A sequence of rectangular boxes ![]() satisfies the property (
satisfies the property (![]() ) if and only if
) if and only if
![]() , where
, where ![]() (resp.
(resp.![]() ) is the length of the smallest (resp. biggest) edge of the box
) is the length of the smallest (resp. biggest) edge of the box![]() .
.
Proof. We calculate the matrix (13).
We fix N and the Nth rectangular box ![]() given by
given by
![]()
Let ![]()
![]() be the center of mass and
be the center of mass and![]() .
.
The substitution
![]()
yields
![]()
where ![]() Since
Since
![]()
and![]() , the matrix (13) becomes
, the matrix (13) becomes![]() . The least eigenvalue of the matrix is equal
. The least eigenvalue of the matrix is equal
to![]() , i.e. to
, i.e. to![]() . The diameter of the box can be estimated above by the constant
. The diameter of the box can be estimated above by the constant
![]() , which also dominates the asymptotics of the diameter. Therefore the condition (
, which also dominates the asymptotics of the diameter. Therefore the condition (![]() ) is fulfilled for the given sequence of rectangular boxes if and only if the sequence
) is fulfilled for the given sequence of rectangular boxes if and only if the sequence ![]() is bounded above. ,
is bounded above. ,
The next lemma is proved in Appendix A.2.
Lemma 2. Assume that the target function ![]() is measurable and bounded on
is measurable and bounded on ![]() and
and![]() .
.
Assume further that the sequence of partitions ![]() (
(![]() ) of
) of ![]() satisfies the condition (
satisfies the condition (![]() ). Then
). Then
the corresponding LS approximations ![]() and
and ![]() are uniformly bounded on
are uniformly bounded on ![]() and
and![]() , re- spectively, i.e. there exist constant
, re- spectively, i.e. there exist constant ![]() and
and ![]() such that
such that
![]()
for all ![]() and all
and all ![]()
![]()
for all ![]() and all
and all ![]()
The main result of this section is the following theorem:
Theorem 4. Let the target function v be measurable and bounded on![]() .
.
1) If the measurable partitions ![]() have the property
have the property ![]() (
(![]() ), then
), then ![]() and
and ![]()
in the ![]() -norm as
-norm as![]() .
.
2) Assume that ![]() is a polyhedral domain in
is a polyhedral domain in![]() , while a sequence of polyhedral partitions
, while a sequence of polyhedral partitions ![]() of
of ![]()
and associated LS piecewise linear approximations ![]() satisfy the criterion (10) for each
satisfy the criterion (10) for each![]() . Assume
. Assume
further that the partitions ![]() (
(![]() ) satisfy the condition (
) satisfy the condition (![]() ). Then
). Then ![]() in the
in the ![]() -
-
norm as![]() .
.
Proof. To prove the first part of the theorem, we apply Lemma 1 and obtain
![]()
as![]() , since
, since ![]() is the LS piecewise power approximation in
is the LS piecewise power approximation in![]() .
.
In the second part of the theorem, we use either Proposition 1 or Proposition 2, which yields the L2- convergence of the LS approximations ![]() to the function
to the function![]() . Applying Lemma 2 we obtain the uniform boundedness of the approximations:
. Applying Lemma 2 we obtain the uniform boundedness of the approximations: ![]() for some M and any
for some M and any![]() . Then we have
. Then we have
![]()
where ![]() The latter estimate is due to the uniform Lipschitz continuity of the function
The latter estimate is due to the uniform Lipschitz continuity of the function ![]() on the interval
on the interval![]() :
: ![]()
This estimate proves the L2-convergence of the LS approximations ![]() to the target function v. ,
to the target function v. ,
4. Uniform Convergence of Approximations
In the previous section we studied convergence of LS approximations in the L2-norm. In many applications, however, it is desirable to consider their uniform convergence. This may be, for instance, of interest if we include the obtained approximations into the models based on differential equations, as it is well-known that convergence of (approximations of) solutions is only guaranteed by the uniform convergence of (approximations of) the right-hand sides.
The main result of this section is formulated in terms of kinetic orders ![]() and
and ![]() of the target function
of the target function ![]() and its piecewise power approximations
and its piecewise power approximations![]() .
.
Theorem 5. Let the target function ![]() be a C1-function (i.e. differentiable with the continuous partial
be a C1-function (i.e. differentiable with the continuous partial
derivatives). Let the sequence of partitions ![]() (
(![]() ) of
) of ![]() have the following two properties:
have the following two properties:
1) The closure of each ![]() coincides with the closure of its interior
coincides with the closure of its interior ![]()
2) ![]() (
(![]() ).
).
Assume, in addition, that for any![]() ,
, ![]() there exist points
there exist points![]() ,
, ![]() such that piecewise power approximations
such that piecewise power approximations ![]() (=
(=![]() on
on![]() ) satisfy
) satisfy
![]() (14)
(14)
Then ![]() uniformly on
uniformly on ![]() as
as ![]()
Proof. We fix N and consider the corresponding partition ![]() of the domain
of the domain![]() . Let
. Let![]() ,
,
![]() ,
, ![]() ,
,![]() . Clearly,
. Clearly, ![]() By assumption, for
By assumption, for
![]() we have
we have ![]() where
where ![]() On the other hand, the mean value theorem yields
On the other hand, the mean value theorem yields ![]() where
where ![]() depends on y. Therefore
depends on y. Therefore
![]()
The uniform continuity of the continuous vector function ![]() on
on ![]() and the property that
and the property that
![]()
imply that, given an![]() , the estimate
, the estimate
![]() (15)
(15)
is fulfilled for sufficiently large N.
Since (15) holds for any ![]() we also obtain that for sufficiently large N
we also obtain that for sufficiently large N ![]() i.e.
i.e. ![]() uniformly on
uniformly on ![]() as
as![]() .
.
As the uniform convergence of the sequence ![]() implies its uniform boundedness, there is M such that
implies its uniform boundedness, there is M such that ![]() for all
for all![]() . Therefore,
. Therefore,
![]()
where![]() . This gives the uniform convergence of
. This gives the uniform convergence of ![]() to v as
to v as ![]() ,
,
Our last result shows that the LS approximations converge uniformly in the scalar case. This is due to the fact that in the scalar case the equalities (14) are always fulfilled.
Corollary 1. Let the target function v be continuous on ![]() (
(![]() ) and
) and![]() . Assume
. Assume
that the sequence of partitions ![]() (
(![]() ) of
) of ![]() has the property
has the property ![]() (
(![]() ).
).
Then for the corresponding LS power approximations ![]() and
and ![]() we have
we have![]() ,
, ![]() (
(![]() ) uniformly on
) uniformly on![]() .
.
The proof of the theorem follows directly from the previous theorem and the following lemma, the proof of which is given in Appendix A.3.
Lemma 3. Let a linear function ![]() be the LS approximation of a
be the LS approximation of a ![]() function
function ![]() on the entire interval
on the entire interval![]() . Then there exist
. Then there exist ![]() and
and ![]() such that
such that ![]()
![]()
5. Discussion and Conclusions
Piecewise power-law representations may be very useful as practical approximations to target functions which are defined analytically or numerically. However, a strict mathematical justification of these approximations is not always paid attention to. Unfortunately, such an analysis is not always straightforward, especially if one puts additional a priori assumptions on the approximations, which is quite common in many applications.
We showed in the present paper that under additional assumptions power approximations do converge to the target function. We studied least-squares and uniform convergence, both of which are widely used (explicitly or implicitly) in applications.
Our analysis dealt with two types of regression: linear regression in the logarithmic space and power-law regression in the Cartesian space. The first procedure has all the advantages of the linear regression, but the transformation back to the Cartesian space distorts the error structure of the problem; the least squares error for the resulting piecewise power-law fitting is in general less accurate than the corresponding error for a power-law regression of the original data. As a partial remedy, it may be advantageous to apply power-law regression to the original data over each of the partition subsets back in the Cartesian space. Yet, being nonlinear regression this procedure is essentially ill-posed. Thus, both kinds of regression have their strong and weak sides, so that the choice between them must be undertaken by modeling consideration.
In many cases, it may also be advantageous to use the classical linear regression in combination with optimal partitions of the operating domain. In the logarithmic space this procedure is again linear and can be auto- matized, but this may also cause several technical problems when proving the convergence of the corresponding approximations.
In the present paper, we offered a partial mathematical justification of the analysis based on piecewise power approximations, stemming from both kinds of regression, by verifying their convergence in the mean-square (L2) and uniform sense. Uniform convergence is e.g. important if target functions are included in differential eq- uations, as it is the uniform, and not L2-convergence, which is inherited by the solutions of the equations. How- ever, a comprehensive analysis of convergence of solutions of differential equations, approximated by piecewise S-systems, is beyond the scope of this paper and will be discussed in a separate publication.
Acknowledgements
The work of the first author was partially supported by a EEA grant coordinated by Universidad Complutense de Madrid, Spain, and by the grant #239070 of the Norwegian Research Council.
Appendix
A.1. Proof of Lemma 1, Section 1
Let us prove the lemma for the domain![]() . Notice that the function
. Notice that the function ![]() is measurable on the compact set
is measurable on the compact set ![]() and satisfies the estimate
and satisfies the estimate ![]() on
on![]() . By Lusin’s theorem, for any N, there is a uniformly continuous function
. By Lusin’s theorem, for any N, there is a uniformly continuous function ![]() on
on ![]() such that
such that ![]() for all N and the Lebesgue measure of the set
for all N and the Lebesgue measure of the set ![]() is less than
is less than![]() . Now, there exists a
. Now, there exists a ![]() for which
for which![]() ,
, ![]()
implies![]() . We define
. We define ![]() for some
for some![]() .
.
Let ![]() be chosen in such a way that
be chosen in such a way that![]() . If
. If![]() , then we have
, then we have
![]()
as ![]() and
and ![]() Therefore, the Lebesgue measure of the set
Therefore, the Lebesgue measure of the set ![]() is less than
is less than![]() , so that the sequence
, so that the sequence ![]() converges to
converges to ![]() in measure, and due to its uniform bondedness, also in the L2-sense on
in measure, and due to its uniform bondedness, also in the L2-sense on![]() .
.
A similar argument applies to the sequence ![]() on
on![]() , where we use the sequence
, where we use the sequence ![]() instead of
instead of![]() .
.
A.2. Proof of Lemma 2, Section 1
Clearly, ![]() is measurable and bounded on
is measurable and bounded on![]() . Let
. Let![]() .
.
Let us fix a partition subset![]() . Our aim now is to find estimates for the norms of orthonormal basis functions
. Our aim now is to find estimates for the norms of orthonormal basis functions![]() ,
, ![]() in the linear subspace of the space
in the linear subspace of the space ![]() consisting of all linear functions and equipped with the scalar product
consisting of all linear functions and equipped with the scalar product
![]()
One basis is given by the set (11). However, this set is not necessarily orthogonal.
First of all, we choose ![]() and observe that its norm is equal to 1. Using the description (11) of the basis functions
and observe that its norm is equal to 1. Using the description (11) of the basis functions ![]() defined via the center of mass we directly deduce from (12) that
defined via the center of mass we directly deduce from (12) that ![]() is orthogonal to any linear combination of the other basis functions. The challenge is therefore to estimate the norms of linear
is orthogonal to any linear combination of the other basis functions. The challenge is therefore to estimate the norms of linear
combinations![]() , where
, where ![]() are real numbers.
are real numbers.
In the proof below we often omit one of the variables in![]() , that is either l, or y, depending on a particular interpretation of this basis. Writing
, that is either l, or y, depending on a particular interpretation of this basis. Writing ![]() means that we regard it as a vector for each particular y, i.e.
means that we regard it as a vector for each particular y, i.e. ![]() (the component
(the component ![]() is excluded in further considerations). Omitting y (
is excluded in further considerations). Omitting y (![]() ) means that we treat
) means that we treat ![]() as a function of y for a given l, i.e. as an element of the space
as a function of y for a given l, i.e. as an element of the space![]() .
.
As![]() , we require the following constraints on the coefficients:
, we require the following constraints on the coefficients:
![]()
where![]() . Therefore,
. Therefore,
![]() (16)
(16)
(where ![]() is the Euclidean norm in
is the Euclidean norm in ![]() and
and ![]() is the scalar product of two vectors) with the constraint
is the scalar product of two vectors) with the constraint![]() .
.
Diagonalization of the symmetric, positive definite matrix ![]() with the help of an orthogonal matrix Q gives the matrix containing the eigenvalues
with the help of an orthogonal matrix Q gives the matrix containing the eigenvalues ![]() of
of ![]() on the diagonal. Putting
on the diagonal. Putting ![]() and using
and using![]() , we obtain from (16) that
, we obtain from (16) that
![]()
with the constraint![]() , where the constant
, where the constant ![]() is evidently an upper estimate for the func-
is evidently an upper estimate for the func-
tions (11) on the partition subset![]() . The maximum value of the expression
. The maximum value of the expression ![]() under the above constraint is
under the above constraint is![]() , where
, where ![]() is the minimal eigenvalue of the matrix
is the minimal eigenvalue of the matrix![]() . Due to the condition (
. Due to the condition (![]() ) we get
) we get
that![]() , where the constant
, where the constant ![]() does not depend on i and N.
does not depend on i and N.
The final step in the proof of the lemma uses the explicit representation of the LS approximation![]() :
:
![]()
where
![]()
Therefore![]() ,
, ![]() (
(![]() ) and
) and
![]()
This implies also the uniform boundedness of the approximations ![]() on
on![]() . The proof of the lemma is complete.
. The proof of the lemma is complete.
A.3. Proof of Lemma 3, Section 4
Let us first prove the existence of![]() . Assume the converse, i.e. that
. Assume the converse, i.e. that ![]() for all
for all ![]() Let for instance
Let for instance ![]() for all
for all ![]() Put
Put ![]() Then the linear function
Then the linear function ![]() satisfies the estimates
satisfies the estimates ![]() Therefore
Therefore
![]()
This, however, contradicts the definition of the least squares approximations. The case ![]() is treated in a similar manner.
is treated in a similar manner.
Assume now that ![]() for all
for all![]() . We shall prove that in this case the graph of the scalar linear function
. We shall prove that in this case the graph of the scalar linear function ![]() intersects the graph of
intersects the graph of ![]() in at least two points from the interval
in at least two points from the interval![]() .
.
From the first part of the proof we know that at least one intersection point does exist. Assume that there is exactly one point ![]() such that
such that ![]() Without loss of generality we may assume that
Without loss of generality we may assume that ![]() where
where![]() . Since
. Since ![]() and
and ![]() for all
for all![]() , we obtain that
, we obtain that ![]() for
for ![]() and
and ![]() for
for ![]() (one of these sets may be empty). Consider a new linear approximation given by
(one of these sets may be empty). Consider a new linear approximation given by ![]() where a sufficiently small
where a sufficiently small ![]() is chosen in such a way that the graphs of the functions
is chosen in such a way that the graphs of the functions ![]() and
and ![]() have still one intersection point in
have still one intersection point in ![]() (namely, d by construction).
(namely, d by construction).
It is easy to see that such a ![]() does exist. Indeed, in a vicinity U of the point d we have that
does exist. Indeed, in a vicinity U of the point d we have that![]() , so that for small
, so that for small ![]() we have
we have ![]()
![]() and hence d is the only intersection point of the graphs of the functions
and hence d is the only intersection point of the graphs of the functions ![]() and
and ![]() in U. Outside U, i.e. inside the compact set
in U. Outside U, i.e. inside the compact set ![]() the continuous function
the continuous function ![]() is non-zero, so that
is non-zero, so that![]() . Choosing
. Choosing ![]() in such a way that
in such a way that ![]() guarantees that the graphs of the functions
guarantees that the graphs of the functions ![]() and
and ![]() meet only in d.
meet only in d.
We complete now our analysis of the scalar case observing that for such ![]()
![]()
simply because the graph of ![]() is closer to the graph of
is closer to the graph of![]() , than the graph of l. This contradicts the assumption that l is the LS approximation of
, than the graph of l. This contradicts the assumption that l is the LS approximation of![]() . We have therefore proved that there exists
. We have therefore proved that there exists ![]() such that
such that ![]()
A.4. Piecewise Power-Law Regression
In this subsection we describe a numerically stable way to find a best possible, in some sense, piecewise power approximation to an arbitrary target function. The method was suggested in [18] and was based on the piecewise linear regression from [19] .
Let![]() ,
, ![]() be a target function (e.g. the in- and efflux functions in (2), possible only as a data set obtained from some measurements. The task is to find a set of power functions which approximate the target function in a “best possible” way given a number N of the partition sets. The problem is essentially non-convex being therefore not well-posed numerically. However, using the logarithmic space
be a target function (e.g. the in- and efflux functions in (2), possible only as a data set obtained from some measurements. The task is to find a set of power functions which approximate the target function in a “best possible” way given a number N of the partition sets. The problem is essentially non-convex being therefore not well-posed numerically. However, using the logarithmic space ![]() one can convert this problem into a linear one. Performing an automated piecewise linear regression based on Artificial Neural Networks (ANN) introduced in [19] , this algorithm returns an optimal polyhedral partition of the domain in logarithmic space and the corresponding optimal set of linear functions which are the best approximations to the image of the target function in the logarithmic space. Returning to the Cartesian space produces piecewise power functions that are not necessarily the best possible approximations in the sense of the metric in
one can convert this problem into a linear one. Performing an automated piecewise linear regression based on Artificial Neural Networks (ANN) introduced in [19] , this algorithm returns an optimal polyhedral partition of the domain in logarithmic space and the corresponding optimal set of linear functions which are the best approximations to the image of the target function in the logarithmic space. Returning to the Cartesian space produces piecewise power functions that are not necessarily the best possible approximations in the sense of the metric in![]() , but this approximation procedure is numerically stable.
, but this approximation procedure is numerically stable.
As before, we assume ![]() to be the image of
to be the image of ![]() under the logarithmic transformation, i.e.
under the logarithmic transformation, i.e. ![]() ,
,![]() . Let also N be a fixed number of partition subsets of a polyhedral set
. Let also N be a fixed number of partition subsets of a polyhedral set![]() . The task is to construct numerically the function
. The task is to construct numerically the function![]() ,
, ![]() , which is piecewise linear and which is the best possible LS approximation to
, which is piecewise linear and which is the best possible LS approximation to![]() . The inverse logarithmic transformation of
. The inverse logarithmic transformation of ![]() will then give a piece- wise power approximation
will then give a piece- wise power approximation ![]() of the target function v, which is best possible with respect to the logarithmic distance. To simplify the notation we will below write
of the target function v, which is best possible with respect to the logarithmic distance. To simplify the notation we will below write![]() , thus removing the index N.
, thus removing the index N.
A polyhedral partition satisfies the following assumptions: ![]() for every
for every![]() ,
, ![]() ,
,
![]() and
and
![]() (17)
(17)
This partition gives rise to a partition of the original domain![]() . Applying the inverse logarithmic trans-
. Applying the inverse logarithmic trans-
formation, we obtain
![]() (18)
(18)
The piecewise linear function ![]() is assumed to have the following representation:
is assumed to have the following representation:
![]() (19)
(19)
where ![]() are all polyhedral sets defined by (17) and defining a partition of the logarithmic domain
are all polyhedral sets defined by (17) and defining a partition of the logarithmic domain![]() .
.
Scalar weights ![]() for
for ![]() and the numbers
and the numbers ![]() for
for![]() ,
, ![]() ,
, ![]() uniquely characterize the function
uniquely characterize the function ![]() and the corresponding partition
and the corresponding partition![]() . Below the weights are collected in a vector
. Below the weights are collected in a vector ![]() for every
for every![]() .
.
The piecewise linear algorithm has two targets.
Target 1: The weights vector ![]() (
(![]() ), which should be reconstructed as soon as the partition is known.
), which should be reconstructed as soon as the partition is known.
Target 2: Scalars ![]() (
(![]() ,
,![]() ) which should be estimated for every
) which should be estimated for every ![]()
The aim of the piecewise linear regression: given a function ![]() represented via a data set
represented via a data set![]() , a number of partition subsets N and a natural number c find a piecewise linear function
, a number of partition subsets N and a natural number c find a piecewise linear function ![]()
and the polyhedral partition ![]() such that
such that
![]()
where the minimum is taken over all polyhedral partitions ![]() and all linear functions
and all linear functions ![]() (
(![]() ). The parameter c is the number of nearest neighboring points required by the implementation of the method. The neighboring points are used to aggregate approximations into clusters.
). The parameter c is the number of nearest neighboring points required by the implementation of the method. The neighboring points are used to aggregate approximations into clusters.
The algorithm consists of the following steps.
Step 1. Local regression: Define the set ![]() containing the kth point
containing the kth point ![]() and the samples associated with
and the samples associated with ![]() nearest neighbors y to
nearest neighbors y to ![]() and perform linear regression to obtain the weights
and perform linear regression to obtain the weights ![]() fitting the samples in
fitting the samples in![]() .
.
Step 2. Clustering: Perform a clustering process to subdivide the set of weight vectors ![]() into N groups with similar features.
into N groups with similar features.
Step 3. Classification: Apply a classification algorithm based on a pattern-recognition method to produce the coefficients ![]() describing the partition subsets
describing the partition subsets![]() .
.
Step 4. Regression: For every ![]() perform linear regression on the samples
perform linear regression on the samples ![]() with
with ![]() to obtain the weights
to obtain the weights ![]() for the ith approximation.
for the ith approximation.
The inverse logarithmic transformation of ![]() results in a piecewise power approximation of the function
results in a piecewise power approximation of the function ![]() and a partition
and a partition ![]() defined by (18).
defined by (18).
A modification of this algorithm, which is suggested in [18] , assumes a power-law regression to the original data over each of the N partition subsets of the optimal partition![]() , so that the increase in difficulty is modest even though the regression is now nonlinear. The partitioning is found from the first three steps of the above algorithm and the new algorithm proceeds as follows:
, so that the increase in difficulty is modest even though the regression is now nonlinear. The partitioning is found from the first three steps of the above algorithm and the new algorithm proceeds as follows:
Step 4A. Power-law regression: For every ![]() perform power-law regression on the samples
perform power-law regression on the samples ![]() with
with ![]() to obtain the power functions for each partition subset given by (18).
to obtain the power functions for each partition subset given by (18).
The algorithm is implemented in a free MatLab toolbox Hybrid Identification Toolbox (HIT).
A.5. Ill-Posedness of LS Power-Law Fitting
In this section we show that the nonlinear power-law regression, i.e. the one based on the minimization criterion (9), is ill-posed. This ill-posedness is caused by the fact that the set ![]() from (9) is a non-convex set.
from (9) is a non-convex set.
Let us assume that ![]() is only known with a certain accuracy, as it is often the case. Mathematically, we will describe this situation by letting v depend on a (small) parameter
is only known with a certain accuracy, as it is often the case. Mathematically, we will describe this situation by letting v depend on a (small) parameter![]() , i.e.
, i.e. ![]() (and so becomes the function
(and so becomes the function ![]() as well). But it turns out, as we will show below, that for certain values of
as well). But it turns out, as we will show below, that for certain values of ![]() small perturbations may cause a “jump” in the corresponding power-law representation, i.e. while functions
small perturbations may cause a “jump” in the corresponding power-law representation, i.e. while functions ![]() remain close to each other, the least-squares minimization criterion (9) may produce the power-law repre- sentations that are very different.
remain close to each other, the least-squares minimization criterion (9) may produce the power-law repre- sentations that are very different.
Below we illustrate this fact analytically using a specific example. For the sake of simplicity, let us consider a target function ![]() of one variable, so that
of one variable, so that
![]() (20)
(20)
If ![]() then
then ![]() and f that minimize (20) are also functions of
and f that minimize (20) are also functions of ![]()
We first consider a simpler problem assuming that![]() , so that after rescaling we may assume that
, so that after rescaling we may assume that ![]() and rewrite (20) as
and rewrite (20) as
![]()
After applying the substitution ![]()
![]()
![]() we obtain
we obtain
![]()
or
![]() (21)
(21)
where ![]()
![]()
Now, let ![]() and consider the function
and consider the function ![]() and its LS power approximation
and its LS power approximation![]() .
.
It is easily seen that the projection function ![]() is discontinuous in
is discontinuous in ![]() (see Figure A1), while Figure A2 gives a graphical representation of this discontinuity in
(see Figure A1), while Figure A2 gives a graphical representation of this discontinuity in ![]() for one value of y.
for one value of y.
Going back to the variable x, the above function becomes![]() ,
, ![]() ,
, ![]() ,
,
the discontinuity in ![]() being preserved.
being preserved.
This example shows that the criterion (9) may produce a LS power approximation that is not stable under small perturbations of the parameter ![]() and by this under small perturbations of the target function, which causes ill-posedness of the minimization problem. We stress also that this effect is generic, i.e. independent of the number of the involved parameters, as the comparison of Figure A1(a) (resp. Figure A1(b)) and Figure A2(a) (resp. Figure A2(b)) clearly demonstrates.
and by this under small perturbations of the target function, which causes ill-posedness of the minimization problem. We stress also that this effect is generic, i.e. independent of the number of the involved parameters, as the comparison of Figure A1(a) (resp. Figure A1(b)) and Figure A2(a) (resp. Figure A2(b)) clearly demonstrates.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/