Error Estimations, Error Computations, and Convergence Rates in FEM for BVPs

Karan S. Surana¹, A. D. Joy¹, J. N. Reddy²

¹Department of Mechanical Engineering, Univeristy of Kansas, Lawrence, KS, USA.
²Department of Mechanical Engineering, Texas A&M University, College Station, TX, USA.

DOI: 10.4236/am.2016.712120                

Abstract

This paper presents derivation of a priori error estimates and convergence rates of finite element processes for boundary value problems (BVPs) described by self adjoint, non-self adjoint, and nonlinear differential operators. A posteriori error estimates are discussed in context with local approximations in higher order scalar product spaces. A posteriori error computational framework (without the knowledge of theoretical solution) is presented for all BVPs regardless of the method of approximation employed in constructing the integral form. This enables computations of local errors as well as the global errors in the computed finite element solutions. The two most significant and essential aspects of the research presented in this paper that enable all of the features described above are: 1) ensuring variational consistency of the integral form(s) resulting from the methods of approximation for self adjoint, non-self adjoint, and nonlinear differential operators and 2) choosing local approximations for the elements of a discretization in a subspace of a higher order scalar product space that is minimally conforming, hence ensuring desired global differentiability of the approximations over the discretizations. It is shown that when the theoretical solution of a BVP is analytic, the a priori error estimate (in the asymptotic range, discussed in a later section of the paper) is independent of the method of approximation or the nature of the differential operator provided the resulting integral form is variationally consistent. Thus, the finite element processes utilizing integral forms based on different methods of approximation but resulting in VC integral forms result in the same a priori error estimate and convergence rate. It is shown that a variationally consistent (VC) integral form has best approximation property in some norm, conversely an integral form with best approximation property in some norm is variationally consistent. That is best approximation property of the integral form and the VC of the integral form is equivalent, one cannot exist without the other, hence can be used interchangeably. Dimensional model problems consisting of diffusion equation, convection-diffusion equation, and Burgers equation described by self adjoint, non-self adjoint, and nonlinear differential operators are considered to present extensive numerical studies using Galerkin method with weak form (GM/WF) and least squares process (LSP) to determine computed convergence rates of various error norms and present comparisons with the theoretical convergence rates.

Keywords

Finite Element, Error Estimation, Convergence Rate, A Priori, A Posteriori, BVP, Variationally Consistent Integral Form, Variationally Inconsistent Integral Form, Differential Operator Classification, Self-Adjoint, Non-Self-Adjoint, Nonlinear

Received 3 June 2016; accepted 26 July 2016; published 29 July 2016

1. Introduction

It is now well recognized that in finite element computations there are three independent parameters: characteristic length of the discretization h, degree of approximation p, and the order k of the scalar product space. h and p have been well known for quite some time but introduction of k as an additional independent parameter in finite element computations is rather recent. Surana et al. [1] - [4] have shown the order k of the approximation space to be an independent parameter in all finite element computational processes in addition to h and p, hence k-version of finite element method in addition to h- and p-versions. The order k of the approximation space ensures global differentiability of order over the whole discretization. The appropriate choice of k is essential in ensuring that 1) the desired physics is preserved in the computational process and 2) the integrals are Riemann in the entire finite element process so that the equivalence of BVP with the integral form is preserved and the errors in the calculated solution can be computed correctly without knowledge of the theoretical solution. We elaborate more on some of these aspects in the following.

If the differential operator contains highest order derivatives of the dependent variables of orders, then the approximation of the solutions of the BVP must at least be of class i.e. of global differentiability of order in order for this approximation to be admissible in the BVP in the pointwise sense. This requires that the order k of the approximation space must at least b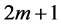e i.e. 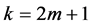is minimally conforming order of the approximation space. Clearly, the order k of the minimally conforming space is determined by the highest order of the derivatives of the dependent variable(s) in the BVP. When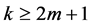, all integrals over the discretization remain Riemann. 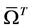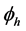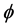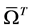When, the integrals over are in Lebesgue sense and the corresponding approximation of the solution over is not admissible in the BVP in the pointwise sense. When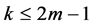, the approximation of over is not admissible at all in the BVP. Choosing may be beneficial if the theoretical solution of the BVP is of higher order global differentiability than 2m as this choice incorporates higher order global differentiability aspects of in the computational process. Thus, now we have h-, p-, k-versions of the finite element processes and associated convergences and convergence rates.

The subject of a priori error estimation and a posteriori error estimation have been exhaustively studied and investigated with the objective that 1) perhaps a priori error estimates will help us in deciding the most prudent choices of h, p, and k so that the errors in the desired norms are reduced at the fastest rate during computations, 2) the a posteriori error estimates will guide us based on the current finite element solution in improving the accuracy of the subsequently computed solutions in the most prudent manner. The published literature on this subject is enormous and discussion of each writing on the subject in this paper is not feasible and is also of little benefit. Interested readers can refer to some selected publications [5] - [34] included here.

In the work presented in this paper, our objectives are:

a) To derive a priori error estimates for BVPs described by self adjoint, non-self adjoint, and nonlinear differential orperators when the theoretical solutions are analytic, thus establishing precise dependence of the chosen error norm on h, p, k, and the smoothness of the theoretical solution (for simplicity this is done using one dimensional BVPs).

b) To discuss the currently used a posteriori error estimation techniques, their shortcomings, and serious inadequacies when actual physics of the BVP is incorporated in the finite element computational process.

c) To demonstrate the need for a posteriori error computation and present a framework in which those computations can be performed without the knowledge of theoretical solutions.

d) To establish that higher order approximation spaces and variationally consistent integral forms are essential for incorporating the desired physics of the BVP in the computational process and to ensure that the resulting finite element computational processes are unconditionally stable so that error estimations remain meaningful.

e) To perform numerical studies using one dimensional boundary value problem described by self adjoint, non-self adjoint, and nonlinear differential operators and to demonstrate exceptionally good agreement of the computed convergence rates with those established theoretically.

f) To establish that the a priori error estimates derived in (a) also hold for 2D and 3D BVPs when the integral forms in those BVPs are variationally consistent.

2. Preliminaries: Convergence and Convergence Rates, Convergence Behavior of Computations, Error Estimation, and Error Computations

In this section, we present some preliminary material and concepts that are essential in error estimation and error computations. Many of these are well known but are included in the following for completeness and for the sake of coherent continuation to the new work in this paper.

2.1. Convergence and Convergence Rate

Convergence of a finite element solution implies behavior of the error in the finite element solution (measured in some norm) as a function of the degrees of freedom or the characteristic length of the discretization. When the theoretical solution is known, the error in the finite element solution in some norm (L₂-norm, H¹-norm, etc.) can be computed and therefore we can study its behavior as a function of the degrees of freedom. When the theoretical solution is not known, perhaps estimating the error in some norm in the computed solution is a viable option. However, we shall see in a later section that this option only works in a restricted range of the behavior of error norm versus dofs. The third option is that if we are using minimally conforming spaces then residual functional can be computed precisely as for minimally conforming spaces all integrals over the discretization of, the domain of definition of the BVP, are Riemann. Proximity of to zero is a measure of error due to the fact that when,. Thus, is in fact error measure in the solution over. This option can always be used for any applications as it does not require theoretical solution but necessitates the approximation to be in a space of order. In what follows we can use as a measure of error over, hence convergence of the computed solution to implies studying versus dofs as more degrees of freedom are added to the discretization. When, a predetermined tolerance of computed zero, we consider the finite element solution to be converged to the

theoretical solution. We consider versus dofs or, L₂-norm of residual E.

We study versus dofs using log-log scale, or more precisely we study versus log(dofs). and log(dofs) or log-log scale are necessary as the range of I could be - and the range of dof could be - or higher.

2.2. Convergence Behavior of Computations

The material presented in this section is based on versus dof behavior, but the same concepts hold true for any other measure of error norm (i.e. can be replaced with any other error norm without affecting the basic behavior of the convergence graph). A typical convergence behavior of or versus log(dof) is shown in Figure 1. This graph is generated using 1D convection-diffusion equation (a second order ODE) with and least squares finite element formulation based on residual functional. The progressively graded discretizations are generated beginning with two elements using a constant geometric ratio of 1.5. The smallest element is located at. is used as it corresponds to the minimally conforming space. Minimum p-level of 5 (needed for) is considered for each progressively refined discretization. From Figure 1, we observe five distinct zones. In each one of these zones the behavior of versus dofs is unique and distinct. The behavior of versus log(dofs) shown in Figure 1 illustrates the varying rate of convergence of the finite element solution (the slope of the curve) with varying dofs. In the middle portion represented by almost a straight line behavior the slope is almost constant, indicating constant convergence rate. We discuss the details related to the varying slope of the curve, associated rate of convergence, and its significance in the following.

Figure 1. Typical convergence behavior of a finite element solution.

Pre-asymptotic range (AB): The range AB is called pre-asymptotic range. In this range as we move from location A toward location B additional degrees of freedom are added to the discretization but there is virtually no measurable reduction in the L₂-norm of E. The accuracy of the computed solution in this range is very poor (due to of the). Due to poor accuracy of the solution, hence, the values for the elements are poor as well, hence these cannot be used to guide any form of adaptive refinement process. A posteriori error estimations in this range are not possible either as these require some regularity in the computed solution which is absent in in range AB. Thus, in this range adaptive processes are not possible as reliable indicators (either estimated or computed) based on are not possible.

Onset of asymptotic range (BC): The range BC is called onset of asymptotic range. In this range addition of degrees of freedom to the discretization results in measurable reduction in reflecting progressive improvement in accuracy of the computed solution from B to C. In this range values or any other possible element error indicators are more accurate than range AB. In this range adaptive processes in h, p, or hp can be utilized keeping in mind that as we move closer to C, the values of (or other indicators) for the elements of the discretization become more accurate, hence can be more effective in the adaptive process.

Asymptotic range (CD): In this range as more dofs are added to the discretization the improvement (reduction) in is most significant. This range on log-log scale is nearly linear, hence constant slope. Adaptive refinements in this range are most effective in reducing. We observe that between C and D there are several orders of magnitude reduction in the value of. Slope of the error norm versus dof graph in this range is called the asymptotic convergence rate of the finite element solution.

Onset of post-asymptotic range (DE): This range is almost reverse of the onset of asymptotic range. In this range reduction in progressively diminishes with the addition of degrees of freedom to the discretization indicating that substantial achievable reduction in has taken place up to point D. Computations in this range result in waste of significant resources (dofs) with very little gain in the objective of reducing.

Post-asymptotic range (EF): In this range in spite of the addition of dofs to the discretization no measurable reduction is observed in. This is generally due to the fact that within the accuracy of the computations (i.e. the word size on the computer we have reached a limit), hence the accuracy remains limited to the same number of decimal places in regardless of the increase in dofs.

2.3. Convergence Rates

In range AB, the slope is almost zero. From B to C the slope increases as more dofs are added to the discretization thereby progressively increasing convergence rate from B to C. From C to D, the asymptotic range, the slope of versus dofs is almost constant and the reduction in is most significant as more dofs are added. Thus, in the asymptotic range the convergence rate is the highest (due to highest slope of versus log(dof)) and is constant. In the onset of post-asymptotic range DE the convergence rate decreases and eventually becomes almost zero in the post-asymptotic range EF.

Remarks

I) Behavior of versus dofs shown in Figure 1 is typical of other error norms as well, hence the discussion and conclusions related to Figure 1 are applicable in the convergence behavior study using any other desired error norm.

II) Pre-asymptotic range AB, onset of post-asymptotic range DE, and post-asymptotic range EF should be avoided as in these ranges solution accuracy improvement is poor.

III) In range AB values (or other measures) are not accurate enough to guide an adaptive process of any kind.

IV) Adaptive processes () can be initiated in the range BC as values in this range are reasonable measure of error. Adaptive processes become more and more effective when we initiate them as we approach from B to C. In the range BC the slope of versus dof increases from B to C indicating improving convergence rate and eventually achieves the highest convergence rate value at C which remains almost constant in the asymptotic range CD.

V) A priori and a posteriori error estimates are only valid in the asymptotic range due to the fact it is only in this range that computed has desired regularity and the convergence rate is the highest, hence worth estimating a priori. The error estimates (a priori and a posteriori) can neither be derived accurately nor can be used meaningfully in regions other than BC.

2.4. Error Estimation and Error Computation

There are two types of error estimations generally considered: a priori error estimation and a posteriori error estimation. A priori error estimation refers to establishing dependence of some error norm on h, p, k, and the regularity of the theoretical solution before the computations are performed so that we have knowledge of the precise nature of the functional dependence of error norm on h, p, k, and the regularity of the theoretical solution. A posteriori error estimation refers to error estimates derived using a computed solution with specific choices of h, p, and k. The sole purpose of a posteriori error estimation is to use current finite element solution to derive element indicators that can perhaps be used to guide an adaptive process. Both of the error estimations require some regularity of the computed solution which only exists in the asymptotic range (range CD, Figure 1). This is a very significant restriction on the use of these estimates. For example, a priori error estimate cannot be used to predict convergence rate in the ranges AB, BC, DE, and EF as this is specifically derived using the regularity of that only exists in the asymptotic range. Likewise a posteriori estimate cannot be used for adaptivity in any ranges except CD.

Another point to note is that a posteriori error estimates are generally derived such that they quantify the

weakness (es) in the finite element global approximation. Their derivations are largely based on

local approximations which result in interelement discontinuity of the derivatives normal to the interelement boundaries. This may be quantified by establishing bounds that can be used for adaptivity. However if we use of class thereby of class, then such bounds are meaningless. In k-version of finite element methods enabling higher order global differentiability approximations, majority of the a posteriori error estimates based on interelement discontinuity of the derivatives are not meaningful. With the use of higher order approximations, the integrals can be maintained Riemann, and are true measures of the error in the finite element solution for and and can indeed be used in adaptive processes. These aspects are discussed in more details in later sections.

3. Variationally Consistent (VC) and Variationally Inconsistent (VIC) Integral Forms

The differential operators appearing in the totality of all BVPs can be mathematically classified in three categories: self-adjoint, non-self-adjoint, and nonlinear differential operators. The finite element processes for these operators can be derived by constructing integral forms using methods of approximation such as: Galerkin method (GM), Petrov-Galerkin method (PGM), weighted residual method (WRM), Galerkin method with weak form (GM/WF), and least squares method or process (LSP). The unconditional stability of the resulting computational process or lack thereof can be established by making a correspondence of these integral forms to the elements of the calculus of variations [1] - [4] [35] . The integral forms that result in unconditionally stable computational processes are termed variationally consistent (VC). The others are called variationally inconsistent (VIC). In VC integral forms the assembled coefficient matrices always remain positive-definite regardless of the admissible choices of h, p, and k whereas in VIC integral forms this can not always be ensured.

Definition 3.1 (consistent (VC) integral form of a BVP) A variationally consistent integral form corresponding to the BVP consists of

1) Existence of a functional corresponding to the BVP. This is generally by construction (or is assumed).

2) Necessary condition for the existence of an extremum of is given by. The integral form is used to determine. The Euler’s equation resulting from must be the BVP.

3), , (minimum, saddle point, maximum of) is the sufficient condition or extremum principle. Extremum principle ensures that a obtained from is unique. Extremum principle also establishes whether from minimizes or maximizes or yields a saddle point of.

When all these three elements are present in an integral formulation of the BVP, then the integral form (resulting from or otherwise) is called a variationally consistent integral form of the BVP (or simply VC integral process). VC integral form or process yields unique extremum of the functional corresponding to, hence a unique solution of the BVP (the Euler’s equation resulting from).

Definition 3.2 (inconsistent integral form (VIC) of a BVP) If an integral form of a BVP (resulting from or otherwise) is not variationally consistent, then it is variationally inconsistent. A variationally inconsistent integral form or process violates one or more of the three requirements needed for variational con- sistency of the integral form.

Remarks

1) Thus, we see that a variationally consistent integral form of a BVP emerges as a method of obtaining a unique solution of the BVP.

2) The necessary condition (the integral form resulting from or otherwise) provides a system of algebraic equations from which the solution is determined.

3) The sufficient condition or unique extremum principle ensures that a obtained from the integral form (or otherwise) is unique, hence this yields a unique extremum of as well as a unique solution of the Euler’s equation which is the BVP under consideration.

4) Variationally consistent integral forms yield symmetric coefficient matrices in the algebraic systems and the coefficient matrices are positive-definite, hence have real, positive eigenvalues and real eigenvectors (basis). Such coefficient matrices are invertible, hence yield unique values of the unknowns in the corresponding algebraic systems.

5) When the integral form is variationally inconsistent, a unique extremum principle does not exist. In such cases the coefficient matrix in the algebraic system resulting from the integral form is not symmetric, hence is not ensured to be positive-definite. A unique solution of the unknowns in such algebraic systems is not ensured. A consequence of the non-positive-definite coefficient matrix in the algebraic system is that such coefficient matrices may have zero or negative eigenvalues or the eigenvalues and eigenvectors may be complex. In summary, variationally inconsistent integral forms must be avoided at all cost due to the fact that when using such integral forms a unique solution of the BVP is not ensured. In other words when obtaining solution of BVPs, variationally consistent integral forms are essential to ensure unique solutions of the BVPs.

6) The definition stated above can be applied to any BVP provided we can show existence of a functional corresponding to the BVP such that and are necessary and sufficient conditions for the existence of extremum of. A yielding unique extremum of is also a unique solution of.

7) We can show (see ref. [1] - [4] [35] for details) that a) the integral forms resulting from GM/WF are VC only for self-adjoint differential operators when the bilinear functional is symmetric, b) the integral form resulting from LSP is VC for all three classes of differential operators, and c) integral forms resulting from the other methods of approximation (GM, PGM, WRM) for all three clases of differential operators are VIC.

8) We show that VC integral forms in designing finite element processes are essential for the derivations of the a priori error estimates.

9) In the following, we only consider GM/WF and LSP, keeping in mind that the integral form from GM/WF is VC only for self-adjoint differential operators and for LSP the integral forms are VC for all three classes of operators.

4. Variational Consistency of the Integral Form and the Best Approximation Property

In this section, we present some theorems and their proofs regarding GM/WF and LSP for the three classes of differential operators and establish best approximation property of GM/WF for self-adjoint operators and LSP for all three classes of operators.

4.1. Galerkin Method with Weak Form (GM/WF): Self-Adjoint Operators

In this section, we revisit main steps of GM/WF for self-adjoint operators. Let

(1)

be a boundary value problem in which the differential operator A is symmetric and its adjoint (i.e. the differential operator A is self adjoint). Based on fundamental lemma of calculus of variations we can write the following integral form [1] [35] :

(2)

in which on if (given) on. v is called test function, hence is admissible in (2). When in (2), the integral form (2) is called integral form in Galerkin method. Since A is self adjoint, the BVP (1) only contains even order derivatives of. We transfer half of the differentiation from to v using integration by parts in the first term in (2) and collect those terms that contain both and v and define them collectively as and those that contain only v and define them as, hence we can write the following.

(3)

Each term in contains both and v but more importantly the orders of derivatives of and v in each term is same (i.e. is symmetric), thus

(4)

and since A is linear, is bilinear in and is linear in v. Hence in this case quadratic functional is possible and is given by

(5)

The integral form (3) is called weak form of (1). Due to the fact that (2) is integral form in Galerkin method, the weak form (3) is called integral form in Galerkin method with weak form (GM/WF). The quadratic functional has physical significance as explained in reference [35] . If (1) represents a BVP associated with

linear elasticity in solid mechanics, then is strain energy, is potential energy of loads and

is the total potential energy of the system described by (1).

Theorem 4.1. The weak form resulting from GM/WF for self adjoint differential operator A in in which is symmetric is variationally consistent.

Proof. Variational consistency of the weak form requires that there exist a functional such that gives the weak form, the Euler’s equation resulting from is the BVP, and yields unique extremum principle. Following Section 4.1 the existence of the functional is by construction (Equation (5))

If is differentiable in, then is a necessary condition for an extremum of. Using (due to GM/WF),

Since is symmetric, we obtain

or

The unique extremum principle (or sufficient condition) is given by

Hence, a unique extremum principle.

To show that the Euler’s equation resulting from the weak form is in fact the BVP, we just have to transfer differentiation back to f (or f_h) from v in the weak form using integration by parts. This is rather straightforward. Thus, the weak form resulting from the GM/WF is variationally consistent. implies that a from the weak form minimizes,

□

Theorem 4.2. Let be a BVP in which A is self adjoint and let be weak form resulting from GM/WF in which and, then has best approximation property in -norm. That is, if, being theoretical solution, then

Proof.

a)

Choosing

Hence,

or

This implies that no element of V is a better approximation of than, the solution for the weak form when measured in as e is -orthogonal to every element v of V. This is called the best approximation property of GM/WF for self adjoint operators.

b) For any

But, hence

Since we have

Thus,

or

or

That is, error in in B-norm is the lowest compared to any other solution w. This completes the proofs of a) and b). □

4.2. GM/WF for Non-Self Adjoint and Non-Linear Operators

Theorem 4.3. Let in be a BVP in which A is a non-self adjoint differential operator. Let be all possible weak forms. Then all such integral forms are variationally inconsistent.

Proof. Let there exist a functional such that yield the weak form. Since A is non-self adjoint, is bilinear but not symmetric (i.e.), hence

is not possible because is not symmetric. Therefore, is not a unique extremum principle. Thus, the integral form with is VIC when the differential operator is non-self adjoint. □

Theorem 4.4. Let in be a BVP in which A is a non-linear differential operator and let be all possible weak forms of in. Then, all such integral forms or weak forms are variationally inconsistent.

Proof. Let there exist a functional such that yields the integral form. Since the differential operator A is non-linear, is linear in v but not linear in and is linear in v. Therefore, the second variation of I

is a function of due to the fact that is a non-linear function of. Thus, does not represent a unique extremum principle and, hence, the integral form or weak form is VIC. □

4.3. Least-Squares Method Based on Residual Functional: Self-Adjoint and Non-Self-Adjoint Operators

Theorem 4.5. The integral form in least-squares method based on residual functional is variationally consistent when the BVP is described by self adjoint differential operator.

Proof. Consider the BVP

in which A is self adjoint. Let be an approximation of over discretization of. Let

be residual function. We define residual functional

If is differentiable in then the necessary condition is given by.

or

or

is bilinear and symmetric and is linear.

Hence, the integral form resulting from is variationally consistent. □

Theorem 4.6. The integral form in least-squares method based on residual functional is variationally consistent when the BVP is described by non-self adjoint operator.

Proof. Since non-self adjoint operators are linear the proof of this theorem is same as that for self adjoint operators (Theorem 4.5) which are also linear. □

4.4. Least-Squares Method Based on Residual Functional for Non-Linear Operators

Theorem 7 Let in be a boundary value problem in which A is a non-linear differential oper-

ator. Let be approximation of in, discretization of and let be the re-

sidual function in. Then the integral form resulting from the first variation of the residual functional set to zero is VC provided and the system of non-linear algebraic equations resulting from are solved using Newton-Raphson or Newton’s linear method.

Proof. Since A is non-linear, E is a non-linear function of, hence is a function of.

If is differentiable in, then

Hence, is a necessary condition.

or

or

Also

is not possible. Hence, we do not have a unique extremum principle. At this stage, the least-squares process is VIC. We rectify the situation in the following.

We note that based on the necessary condition must hold. Since is a non-linear function of, we must find a iteratively that satisfies. Let be an initial (or assumed) solution, then

Let be a change in such that

Expanding in Taylor series about and retaining only up to linear terms in (Newton- Raphson or Newton’s linear method)

Therefore

But. Hence

Thus, in order for the coefficient matrix to be positive-definite,

This gives a unique extremum principle. The improved value of is given by

We choose such that. This is referred to as line search. With this approximation of, the integral form is variationally consistent. £

Remarks

1) Justification for approximating is important to discuss.

2) We note that

Justification of is only necessary in the asymptotic range of convergence as the a priori error estimation only holds in this range, thus establishing best approximation property of LSM method in some norm is also only required in this range.

In the asymptotic range in the pointwise sense if the approximation spaces are minimally conforming to ensure that all integrals over are Riemann. When then, hence is valid. Further discussion on the validity of this approximation can be found in reference [35] .

Theorem 4.8. The integral form resulting from the least-squares method based on residual functional has best approximation property in L₂-norm of E.

Proof. From Section 4.3, we have

or

For theoretical or exact solution, we have

Hence,

Thus, or is orthogonal to (dual of). We note that

That is L₂-norm of E obtained using f_h is lowest out of all. Hence, LSP has best approximation property in L₂-norm of E or. £

Theorem 4.9. A variationally consistent integral form has a best approximation property in some associated norm. Conversely, if an integral form has a best approximation property in some norm, then it is variationally consistent.

Proof. Proof of this theorem follows due to the fact that VC integral form in GM/WF has best approximation property in B-norm because is bilinear and symmetric. The integral form in the LSP is also VC but LSP has best approximation property in L₂-norm of E. Both GM/WF and LSP are VC but have best approximation property in different norms. In both cases, VC integral form is not possible without best approximation property and the best approximation property is not possible without VC integral form. This is obviously due to the fact that they both require the functional to be bilinear and symmetric. As long as this holds, how is derived is not important. £

We note that

1) Since the integral forms for non-self adjoint and non-linear differential operators are VIC in GM/WF, the approximation from GM/WF does not have best approximation property in B-norm (Theorem 4.9).

2) Lack of best approximation property and lack of VC of the integral form resulting from GM/WF for non- self adjoint and non-linear differential operators are both obviously due to the fact that the functional in the weak forms is not symmetric.

3) In LSP for all classes of differential operator is minimized, therefore has best approximation property in E-norm

.

4) We note that variational consistency of the integral form holds for all choices of h, p, and k whereas the best approximation property only holds in the asymptotic range.

4.5. Integral Forms Based on Other Methods of Approximation

The integral forms used in finite element method based on Petrov-Galerkin method, Galerkin method, and weighted residual method are not considered as these always yield integral forms that are variationally inconsistent. Hence, when using these integral forms computations may not even be possible.

4.6. General Remarks

1) We have established that GM/WF yields VC integral form only for self adjoint operators when the functional in the integral form is symmetric and this method has best approximation property in B-norm.

2) LSP based on residual functional yields VC integral forms for self adjoint, non-self adjoint, and non-linear (in the asymptotic range) differential operators and has best approximation property in E-norm.

3) VC integral form implies best approximation property in some norm and vice versa.

4) Best approximation property is necessary in a priori error estimation (in the asymptotic range), as shown in subsequent sections.

5) In general, when using GM, PGM, WRM, etc. error estimation is not possible as in these methods the approximation of does not have best approximation property in any norm.

5. A Priori Error Estimates: GM/WF and LSP

We consider simple model problems to demonstrate the best approximation properties of GM/WF for self adjoint operators and LSP for linear operators and present derivations of the a priori error estimates and convergence rates when. These estimates are derived using model problems (as illustrations) and are then generalized for all BVPs.

5.1. Model Problem 1: GM/WF

Consider the following BVP:

(6)

(7)

GM/WF for (6) with BCs (7) gives

(8)

Let be the finite element approximation of, then we have

(9)

Using (8) and (9) and since, v in (9) is also in V and we have

(10)

Theorem 5.1. For any we have

Proof.

Since

we can choose as both, then

Hence,

Using Cauchy-Schwarz inequality [35]

or

or

That is, in this case for the model problem (6) - (7) the derivative of has the best approximation property in L₂-norm. Alternatively, has best approximation property in B-norm. This completes the proof. £

5.2. Model Problem 2: LSP

Consider the following BVP described by non-self adjoint differential operator.

(11)

(12)

LSP based on residual functional gives (for)

(13)

is approximation of over. This integral form is VC. Also for theoretical solution

(14)

Setting in (14)

(15)

Subtracting (13) from (15)

(16)

Using interpolant of (interpolant matches at end nodes);, let, then we have

(17)

We note that, hence

(due to (5.11)) (18)

Thus, (17) reduces to

(19)

Using Cauchy-Schwarz inequality

(20)

Thus,

(21)

That is L₂-norm of the derivative of error is bounded by the finite element interpolant. Using proposition 5.1 (shown subsequently) and (21), we can write

(22)

L₂-norm of e; that is, for LSP is derived using Aubin-Nitsche trick (Oden and Carey [33] and Reddy [34] ). We consider details in the following.

Consider the same BVP (for),

(23)

Let. Assume that w is the solution of the second order differential equation

(24)

The finite element interpolant () satisfies

(25)

(using (5.19)) (26)

Consider

(27)

Using integration by parts and the fact that at and at and (orthogonal property)

(28)

Hence, (using Cauchy-Schwarz inequality)

(29)

Dividing by

(30)

We make the following remarks.

1) For a first order BVP, the rate of convergence of the L₂-norm of the error in the finite element solution is proportional to and the rate of convergence of the L₂-norm of the derivative of the error is proportional to h.

2) These estimates are same as those for a second order BVP when using GM/WF in which the integral form is variationally consistent.

General Remarks

1) The error estimates have been derived for a second order BVP using GM/WF in which the integral form is VC and the local approximation is linear () over an element. In case of LSP the BVP is first order ODE, the integral form is VC, and for local approximation.

2) We note that the integral forms in both cases are VC and contain only up to first order derivatives, hence the reason for same convergence rates of and even though in case of GM/WF the BVP is a second order ODE and in case of LSP it is only a first order ODE. This is rather significant to note that VC of the integral form and the highest order of the derivative in the integral form control the rates of convergence.

3) We need to extend these estimates for higher degree local approximation (i.e. p-level of “p”).

4) The order of approximation space k needs to be incorporated in the error estimates.

5.3. Proposition and Proof

Proposition 1 Let the theoretical solution of (6) - (7) be at least of class and let be approxi-

mation of over the discretization of in which is an element e. Let h be the characteristic length of such that. Let be interpolant of that agrees

with at the nodes [i.e.,]. Then

a)

(31)

b)

(32)

c) When (31) and (32) hold, the following hold

(33)

(34)

(35)

in which

(36)

Proof. Consider linear and (i.e.).

For an element e let be the interpolation error between f and inter-

polant. Since vanishes at and of an element e, by virtue of Rolle’s theorem there ex- ists at least one point between and at which. Then for any x

(37)

Since is linear, implies that

(38)

Applying Cauchy-Schwarz inequality to (37) and using (38)

(39)

(40)

(41)

(42)

or

(43)

Let

(44)

Hence for, we can write

(45)

This proves (32).

Likewise (since),

(46)

Applying Cauchy-Schwarz inequality

(47)

Substituting from (43) into (47)

(48)

Hence,

(49)

Using (44), (49) reduces to

(50)

This proves (31):

(51)

Substituting from (40) into (51)

(52)

(53)

(54)

(55)

Thus,

(56)

Hence,

(57)

This proves (33).

Consider

(58)

or

(59)

Using Cauchy-Schwarz inequality

(60)

(61)

Substituting from (40)

(62)

(63)

(64)

(65)

(66)

(67)

Hence

(68)

Now

(69)

Using (56) and (68), we have

(70)

(71)

(72)

Hence

(73)

This proves (35).

Remarks

From theorem 5.1, we have

(74)

and

(75)

Hence using (74), (75), (33), and (34), we finally have

(76)

and

(77)

and likewise

(78)

5.4. Proposition and Proof

Proposition 5.2. The derivation of the error estimates in proposition 1 are presented for model problem 1 using GM/WF in which the operator is self adjoint, hence the weak form is VC. In model problem 2 (Section 5.2) the differential operator is non-self adjoint and the error estimates are derived for LSP in which the integral form is also VC. In this section we consider a more general approach of deriving a priori error estimates for arbitrary degree of approximation p only based on the assumption that the integral form is VC.

If the integral form resulting from a method of approximation is VC, then the following hold.

(79)

And if

(80)

then

(81)

In (81), is the highest order of the derivative in the differential operator A. The constants, , , and do not depend upon h and p.

Proof. Consider one dimensional BVP:

(82)

Let be discretization of in which is an element e. Let be finite element approximation of over such that in which is local approximation of over.

Let and be interpolants of of class over and such that at the nodes agrees with the theoretical solution. Thus, error estimation reduces to estimating error between and over an element of length. When is analytic, it can be expanded in Taylor series in over about some point j.

(83)

Consider a over of degree p resulting from a VC integral form (hence, ensuring well-behaved solution), then the local approximation at the same point j can also be written as (assuming agrees with up to degree of p),

(84)

Subtracting (84) from (83), we obtain

(85)

(86)

(87)

Let

(88)

Then

(89)

Therefore

(90)

Using (83)-(90), it is rather straightforward to establish

(91)

and by induction

(92)

Using (90) and (92), we can establish that

(93)

£

Remarks

1) The estimates in (92) and (93) apply to VC integral forms regardless of the method of approximation. Thus, these estimates hold for GM/WF for self adjoint operators and also hold for LSP for all three classes of differential operators.

2) The local approximations used are always of class.

3) The constants, , and do not depend on h and p.

4) The estimates (92) and (93) apply to all finite element processes in which the integral form is variationally consistent.

5) From (92) and (93), we note that progressively increasing order of derivatives of the finite element solution converge progressively slower. That is

(94)

(95)

and so on. Likewise

(96)

(97)

and so on. From (95) and (97), we note that convergence rate in H¹-norm is controlled by the convergence rate of the seminorm (i.e. highest order derivative in). This property holds universally for all operators and integral forms as long as they are variationally consistent.

6) When examining, if the highest order of derivative in E is 2m, then we have

(98)

5.5. Convergence Rates

In this section, we present details of the convergence rates of various error norms for finite element solutions obtained using GM/WF for self adjoint operators when is symmetric and LSP for all three classes of differential operators. We recall that when the integral form has best approximation property in some norm, hence is variationally consistent, we have the following a priori error estimate (derived for 1D BVP, Equation (93)) in the asymptotic range:

(99)

Taking log of both sides

(100)

or

(101)

in which

(102)

We note that (101) is the equation of a straight line (when we use equality) in xy-space in which m is the slope and C is the y-intercept. That is, if we plot versus on an xy-plot, then we obtain a straight

line whose slope is and intercept is. Slope is called the rate of conver-

gence of. Higher values of imply faster convergence of to measured in. Equation (101) can be expressed in terms of total degrees of freedom which is perhaps more appealing in applications as dofs are more easily accessible than characteristic length or size “h” of the discretization. As the discretization is refined, the characteristic length h reduces and the total dofs increase, thus dofs are inversely proportional to h,

(103)

Using in (100) and since we obtain

(104)

We keep in mind that dofs in (104) are purely due to uniform mesh refinement. Thus, in order to determine convergence rate of for finite element processes with VC integral forms we need to plot versus and determine the slope of this curve, which is the convergence rate in the asymptotic range. For a sequence of fixed discretizations, as p increases convergence rate increases linearly.

Remarks

I) We note that requires knowledge of theoretical solution, which may not be possible to determine for a practical application.

II) When the approximation space is minimally conforming or of higher order (i.e. for integrals over to be Riemann or if the Lebesgue integrals over are accepta-

ble), then in which the residual function can be computed using over

and over.

(105)

using and taking log of both sides

(106)

The dofs in (106) are also due to uniform h-refinement. Since does not require theoretical solution,

it can be computed using. Equation (106) can be used for any application without the knowledge of

theoretical solution as long as the approximation space is minimally conforming or of higher order than minimally conforming.

5.6. Proposition and Proof

Proposition 5.3. When local approximation is of progressively higher order global differentiability, that is, in scalar product spaces for progressively increasing k, the accuracy of the finite element solution progressively improves. In this proposition we answer two important questions:

1) Dependence of the a priori error estimates derived so far for local approximations of class on the order of the space k; that is, if the local approximations are in space how do the a priori estimates change and the influence of k on convergence rate.

2) The influence of the order k of the approximation space on the accuracy of the finite element computation.

Of course (1) and (2) are interdependent because when we have determined (1), the assessment of accuracy may be inferred from it.

The following a priori error estimate derived for 1D BVPs using p-version local approximation can be extended when the local approximations are in spaces using the following two important considerations or properties of local approximations in spaces:

(107)

Property I

We consider a simple illustration of a 1D discretization using three node p-version hierarchical local approximation finite elements in space. Let m be the number of elements in the discretization, then the total degrees of freedom (dofs) are given by

(108)

p is the degree of local approximation (assumed same for all elements of the discretization). Let us choose a p-level, say nine (9) and a one hundred (100) element discretization, then using (108) we can determine total degrees of freedom for corresponding to the local approximations of class, , ∙∙∙,.

From Table 1, we observe that as k increases (i.e. progressively higher order local approximations) the total degrees of freedom are progressively reduced. This is a significant property of the higher order local approximations. From Table 1, we note that for, 901 dofs are reduced to 802 in the case of without much effect on accuracy of the solution. The same holds for progressively higher order local approximations, , and so on; that is, the dofs continue to reduce with progressively increasing order of space without much effect on the accuracy. This behavior of the solution accuracy (say in) holds regardless of the type of differential operator and regardless of the method of approximation used to oconstruct the integral form as long as the integral form is variationally consistent. Figure 2 shows typical plots of versus dofs at for solutions of classes, , and. Typical points A, B, C correspond to solutions of classes, , and for the same discretization and p-level (i.e. fixed h and p), with almost same value of but progressively reducing degrees of freedom. In view of the a priori error estimate (107) we can conclude that if h and p are fixed, then the dependence of the a priori estimate on k lies in, [i.e. in (107) and in (98)].

Property II

If we choose and if is the interpolant that agrees with at the inter-element

nodes of the discretization; that is, agree with corre-

sponding to local approximations of classes respectively, then in the consideration of the a priori error estimates we only need to consider () (i.e. interior of the element). This suggests that in a priori estimate in (98) (for example) only depends on k. That is, (98) holds when except that.

Table 1. Total dofs for a 100 element discretization at p = 9 for different values of the order of space k.

Figure 2. Typical versus dofs behavior for k = 1, 2, and 3.

Remarks

1) From properties I and II it is clear that when, in the error estimate (98) the terms and likewise the terms in (107) remain unaffected. Only the coefficients and show mild dependence on k.

2) In view or properties I and II, we conclude that if solutions of a BVP are to be computed for a fixed number of degrees of freedom, then progressively more degrees of freedom can be added to solutions of class so that the total dofs in all classes of solutions are the same. We recall that with same values of h and p in the solutions of class (Figure 2) remains virtually the same for all classes, however the total dofs are progressively reduced.

The consequence of adding more dofs (through h-refinement) with progressively increasing order of space so that in each case the dofs match with C⁰ solutions is clearly improved accuracy of reflected by progressively reducing. Clearly, in doing so the convergence rate or is not affected. Thus, versus log(dofs) graphs for solutions of classes in the asymptotic range are parallel to each other but with progressively lower values of as shown in Figure 2. That is graph for C¹ is below C⁰ and that of C² is below C¹ and so on, but they are all parallel.

5.7. General Remarks

2) We remark again that the rates only hold in the asymptotic range.

3) The integral forms must be VC so that the best approximation property of holds in some norm in order for these estimates to remain valid. The estimates derived here hold for: (a) GM/WF for self adjoint operators when the bilinear functional is symmetric and (b) for LSP based on residual functional for all three classes of differential operator.

4) In case of GM/WF for non-self adjoint and non-linear operators, the a priori estimates derived here do not hold. In case of such operators the functional generally consists of a symmetric part and a non-symmetric part. With sufficient mesh refinement if we can ensure that the behavior is dominated by the symmetric part, then the estimates derived here hold in the range of calculations when asymptotic range is realized. We illustrate this aspect through model problems presented in a later section.

6. Computations of a Priori Error Estimates and Convergence Rates

In this section, we present numerical studies related to the computation of a priori error estimates and convergence rates for BVPs described by self adjoint, non-self adjoint, and non-linear differential operators in which VC integral forms are constructed using GM/WF for BVP described by self adjoint differential operators and using LSP for BVPs described by all three classes of differential operators.

6.1. Model Problem 1: Self-Adjoint Operator, 1D Diffusion Equation

We consider the 1D steady-state diffusion equation.

(109)

(110)

If we choose, , , , then the theoretical solution or is given by

(111)

a) GM/WF: The differential operator is linear and. The integral form using GM/

WF is given by (over)

(112)

or

(113)

is bilinear and symmetric and is linear. The integral form (weak form) is VC due to the fact that

hence a solution from (113) minimizes.

b) LSP based on residual functional

I) LSP using higher order system (without auxiliary equation)

Using (109), referred to as the higher order differential equation or system, if we let be approximation of over then

(114)

(115)

or

(116)

or

(117)

(118)

Hence, the integral form (117) is variationally consistent.

II) LSP using first order system

Let, hence (109) can be written as a system of two first order equations.

(119)

LSP for (119) follows standard procedure. Let and be approximations of and, then

(120)

(121)

(122)

Hence the integral form (121) resulting from LSP is variationally consistent.

Remarks

I) All other methods of approximation yield VIC integral forms, hence are not considered as in such cases the a priori error estimates and the convergence rates are not valid.

II) In the numerical studies, we consider GM/WF and LSP for higher order as well as first order system of differential equations describing BVPs.

6.1.1. GM/WF

In this section, we present numerical studies for the integral form (112) for, discretization of

. We consider uniform discretizations employing three node p-version hierarchical 1D elements with local approximations in scalar product space. We begin with two element uniform discretization and perform uniform mesh refinement containing 4, 8, 16, ...elements. Since in this model problem the theoretical solution is known, various error norms can be computed. We note from the description of the BVP (109) that in this case (highest order of the derivative in the BVP) and the integral form resulting from GM/WF contains only up to first order derivatives of the dependent variable and the test function. We consider computations using solutions of class, , and at different p-levels with uniform mesh refinements. Computed results for solution of class are shown in Figure 3. The integral form is VC and, the computed solution, has best approximation property in -norm.

In this case, the following a priori error estimates hold (Proposition 5.2):

(123)

For this BVP, and q depends on the type of norm. Figure 3 also shows the theoretical values of the convergence rates of various error norms for solutions of class at p-levels of 2 and 5. Graphs of the log of error norms versus log of dofs for these solutions are shown in Figure 3. We note that due to smoothness of the theoretical solution even the two element discretization yields the error norms in the asymptotic range; that is,

Figure 3. versus log(dofs) for solutions of class C⁰ (GM/WF, model problem 1, and 5).

pre-asymptotic and onset of asymptotic ranges in these solutions do not appear in Figure 3. All computations are in the asymptotic range, hence onset of post-asymptotic and post-asymptotic ranges are also absent. Calculated convergence rates are in perfect agreement with the theoretical convergence rates calculated using (123). We note that in and error norms the integrals over are Lebesgue, but the norms are well- behaved due to smoothness of.

Figure 4 shows plots of log of various norms and seminorms versus log of degrees of freedom at and 5 for solutions. The computed convergence rates of various error norms and comparison with the theoretical convergence rates obtained using (123) are shown in Figure 4. The agreement is perfect. Here we note that in computing and, the integrals over are Lebesgue but error norms are well-behaved due to smoothness of. Also, nearly all computations shown in Figure 4 are in the asymptotic range, except for the last point for at and at.

Log of various error norms and seminorms versus log of degrees of freedom for solutions of class at and 7 are shown in Figure 5. Since for, all integrals in all error norms are Riemann over the discretization. Computed error norms using (123) and comparison with the computed convergence rates of error norm are also shown in Figure 5. We observe perfect match between the theoretical values and the computed values. Except for the last point shown in Figure 5 for at, all other computed results are in the asymptotic range due to smoothness of.

Figure 6 shows plots of (or) versus log of dof for solutions of class, , and

() at. All three graphs of versus log of dofs for are parallel, confirming that the convergence rate of is independent of the order k of the approximation space. We note that graph for appears below and the graph for is below confirming that for given dofs, as the order k of space is increased, the error in the computed solution (measured in -norm) decreases without affecting the convergence rate.

The BVP in this model problem is described by a second-order differential operator (); hence, corresponds to minimally conforming space for which the integrals are always Riemann. However, due to smoothness of, when (solutions of class) in which case the integrals over are Lebesgue, the solution is expected to converge weakly to class. Next we consider solutions of class

Figure 4. versus log(dofs) for solutions of class (GM/WF, model problem 1, and 5).

Figure 5. versus log(dofs) for solutions of class (GM/WF, model problem 1, and 7).

Figure 6. versus log(dofs) for solutions of classes C⁰, C¹, and C² at (GM/WF, model problem 1).

with (minimum). Numerical solutions are computed for uniform mesh refinements beginning with a two-element uniform discretization. For each discretization we calculate and. Since the rate of convergence of is controlled by, we expect the convergence rates of and to be nearly same. We clearly see this in Figure 7. Graphs for and are parallel, confirming the same convergence rates of (or) for solutions of class () and class (). The convergence rate in the case of is, whereas in the case of is. Plots in Figure 7 confirm that rate of convergence of error norms is independent of the order of the approximation space.

6.1.2. LSP, Higher-Order System (No Auxiliary Equation)

In this study, we consider finite element formulation of model problem (109) using least-squares process based on residual functional. We consider solutions of class as well as. In case of solutions integrals over are Lebesgue whereas for solutions of class the integrals are Riemann. Figure 8 shows plots of and versus log of dofs for p-levels of 3 and 5 calculated using uniform mesh refinement. Calculated convergence rates of various error norms are also shown in Figure 8. The theoretical convergence rates of various error norms and a comparison with calculated convergence rates is also shown in Figure 8.

Agreement between theoretical and calculated values is excellent. Here also we observe absence of pre- asymptotic and onset of asymptotic ranges due to smoothness of the theoretical solution. Some graphs for significant refinement show appearance of post-asymptotic (or onset of post-asymptotic) range.

Similar studies for solutions of class are shown in Figure 9 for;,; and, norms at p-levels of 5 and 7. The computed convergence rates of the error norms are in perfect agreement with theoretical rates calculated using (), shown in Figure 9.

Graphs of and (or) versus log of dofs for solutions of class and obtained using uniform mesh refinement are shown in Figure 10. Calculated convergence rates are also shown in Figure 10. For error norm the theoretical rate is () whereas for it is (). The theoretical convergence rates are in perfect agreement with those calculated using graphs in Figure 10. We note that

Figure 7. or versus log(dofs) for solutions of classes C¹ and C at (GM/WF, model problem 1).

Figure 8. versus log(dofs) for solutions of class C¹ (LSP, model problem 1, and 5).

Figure 9. versus log(dofs) for solutions of class C (LSP, model problem 1, p = 5 and 7).

Figure 10. or versus log(dofs) for solutions of classes C¹ and C² at p = 5 (LSP, model problem 1).

and graphs for same p-level (5) are parallel to each other and graph is below, confirming that the convergence rates for and are same (i.e. independent of k), the order of space, but for the solution has better accuracy compared to.

Remarks. Numerical studies for LSP using auxiliary equation (i.e. a first-order system) are not presented for this model problem but will be presented for the next model problem, 1D convection-diffusion equation.

6.2. Model Problem 2: Non-Self-Adjoint Operator, 1D Convection-Diffusion Equation

We consider 1D convection-diffusion equation described by non-self adjoint operator for computing a priori error estimates and convergence rates and compare them with their theoretical values,

(124)

(125)

We consider. Theoretical solution of (124)-(125), finite element solution using GM/WF and LSP using higher order system (no auxiliary variables) and using first order system (using auxiliary variables) is

given in [35] . For this BVP, the operator is linear but, hence the in-

tegral form from GM/WF is VIC, but LSP for higher order as well as first order system of differential equations is VC.

a) GM/WF: The integral form of (124)-(125) is given by (for)

(126)

(127)

is bilinear but not symmetric and

(128)

does not yield a unique extremum principle. Hence, the integral form (127) is VIC.

b) LSP based on residual functional:

I) Higher order system (without auxiliary equation)

In this case we use (124) without introducing auxiliary equation, that is without reducing (124) into a first order system of equations. Let be approximation of over, then

(129)

(130)

or

(131)

or

(132)

(133)

Hence, the integral form (132) is VC.

II) First order system

Let, hence (124) can be written as

(134)

LSP for (134) follows standard procedure (parallel to Equations (119)-(122)). Details are straightforward. See [35] for many model problems of similar type.

Remarks

1) Since GM/WF yields VIC integral form and does not have best approximation property as the operator A is not self adjoint, hence the a priori error estimates derived in earlier sections using best approximation property in B-norm do not hold in this case. Nonetheless we present numerical studies for GM/WF for this model problem to illustrate some important aspects of error norms in a later section.

2) Integral form derived using LSP is VC and has best approximation property in E-norm or, I being residual functional, hence the same a priori error estimates derived for LSP for self adjoint operators hold here as well.

6.2.1. LSP: First Order System

Domain is discretized using 3-node p-version 1D elements of higher order global differentiability into 2, 4, 6, ...element uniform meshes. The solutions are computed using finite element formulation based on LSP for first order system of equations. Solutions of classes, , and are considered at different p-levels. For this problem the a priori estimates (123) hold as well with due to the fact that it is a first order system of equations. LSP has best approximation property in E-norm and the integral form is VC,

(135)

First, we consider solutions of class at and 5 and with. Due to local approximation and the first order system, integrals over are Lebesgue but due to smoothness of weak convergence of computed to class is expected. Figure 11 shows plots of log of various error norms versus log of the dofs at and 5. Details of the studies are also given in Figure 11. Theoretical convergence rates are in perfect agreement with the calculated rates shown in Figure 11. As p-level is increased from 2 to 5 convergence rates also show increase by 3 at compared to those at. We clearly observe pre- asymptotic, onset of asymptotic, and asymptotic ranges in all cases. For also observe onset of post- asymptotic and post-asymptotic ranges. We note that even though LSP does not have best approximation property in B-norm but due to the fact that the integral form is VC, the convergence rate of LSP (135) is same as those of GM/ WF for self adjoint operators (123).

As p-level is increased convergence rate increases proportionately. Derivatives converge more slowly than functions, hence convergence rate of is one order lower than that of or. Since the convergence rate of is dominated by the first derivative, and have same convergence rates (also clear from (135)).

Solutions of class at and 5 are considered here. Results obtained using uniform mesh refinement are given in Figure 12. Plots of log of various error norms versus log of dofs and calculated convergence rates are shown in Figure 12 and are compared with theoretical convergence rates. Calculated and theoretical convergence rates are in perfect agreement. We note that when the convergence rates of error norms are independent of k (i.e. at), solutions of class and have same convergence rates for the same norm, confirming that convergence rates of the error norms are not a function of k, the order of the approximation space. Pre-asymptotic, onset of asymptotic, and asymptotic ranges are clearly observed in Figure 12.

Solutions of class at and 7 are considered next. Results obtained using uniform mesh refinement are shown in Figure 13 and are compared with the theoretical convergence rates obtained using (135). Once

Figure 11. versus log(dofs) for solutions of class C⁰ (LSP, model problem 2, first order system, and 5,).

Figure 12. versus log(dofs) for solutions of class C¹ (LSP, model problem 2, first order system, and 5,).

Figure 13. versus log(dofs) for solutions of class C² (LSP, model problem 2, first order system, and 7,).

again the agreement is perfect. Again, we note from Figure 12 and Figure 13 that at the convergence rates are independent of k. In this case, the integrals in the computations of the error norms are always Riemann.

Figure 14 shows plots of and versus log of dof for solutions of class and at. Since the differential operator has the highest derivative of order 2, the convergence rate of is expected to be same as that of or for both classes of solutions. This is confirmed in Figure 14. Convergence rate in case of and solutions are same (4 in this case), but solutions have better accuracy for a given dofs, confirming again that convergence rates of error norms or residual functional are not a function of the order k of the approximation space. Calculated rates are in perfect agreement with the theoretical rates. Figure 15 shows plots of log of versus log of dofs for solution of classes, , and at. We observe same convergence rates for, 2, and 3 but better accuracy of the solution with progressively increasing k. These rates for LSP match perfectly with GM/WF for self adjoint operators due to the fact that in both cases the integral forms are variationally consistent. This proves again that the best approximation property in B-norm is not a requirement for establishing convergence rate. It is the variational consistency of the integral form that matters. Clearly the LSP does not have best approximation property in B-norm, yet has same convergence rates as GM/WF for self adjoint operators due to the fact that in both cases the integral forms are variationally consistent.

6.2.2. GM/WF

Since the differential operator is non-self adjoint the GM/WF will yield VIC integral form in which is nonsymmetric and we lose the best approximation property in B-norm. Nonetheless we conduct some numerical experiments to monitor convergence rates of various error norms. First, we note that GM/WF in this model problem will yield the following element equations for an element e (when and). See reference [35] .

Figure 14. versus log(dofs) for solutions of classes, , and at (LSP, first order system, model problem 2).

Figure 15. or versus log(dofs) for solutions of classes and at (LSP, first order system, model problem 2).

(136)

and the assembled equations for discretization are

(137)

in which and, are due to assembly of and for. As shown in reference [35] , is due to convection term (i.e.) and is due to diffusion (i.e.); is

nonsymmetric with zeros on the diagonals after and BCs are imposed, thus if is large, the contribution of to is almost insignificant compared to the contribution of and the computations using (137) will fail. On the other hand if the discretization is sufficiently refined, the con-

tribution of to overshadows that of and the behavior will be dominated by (i.e.

term in the differential operator). When this happens the integral form from GM/WF will behave like a VC inte-

gral form as it is primarily due to term in the differential operator which is self adjoint, hence the

convergence rates of various error norms will be similar to GM/WF for self adjoint operator.

For numerical experiments, we consider and. For the solution gradients are more isolated near and are higher in magnitude compared to. We consider solutions of class at for both Peclet numbers. Progressively refined uniform discretizations are used for computing solutions and error norms. Figure 16 shows error norms versus dof plots for solutions of class, for. We note that due to smoothness of the solutions, the asymptotic range in which dominates is quickly achieved, and the computations succeed for meshes of 16 elements or more. In this range calculated convergence rates match perfectly with the theoretical rates for self adjoint operator. In this range the BVP re-

duces to as the contribution of term in this range is insignificant. For meshes with 16 ele-

ments or fewer the calculated solution from (137) does not satisfy (137) when substituted in them, implying lack of equilibrium due to spuriousness of the computed solution. Figure 17 shows similar graphs for. The computations fail for discretizations resulting in (meshes coarser than 256 elements) where equilibrium is not achieved, that is, calculated solution from (137) does not satisfy (137) when substituted into the equations. This is due to VIC nature of the integral form resulting from GM/WF. Correspondingly, the values of the error norms for the failed discretizations grow out of control. When (discretization contains 256 elements or more), contribution becomes insignificant and the BVP behaves like

, hence the asymptotic range is observed with calculated convergence rates of the indicated error

norms of 3.7, 2.9, 2 are achieved compared to their theoretical values of 4, 3, 2 for self adjoint operators, rather amazingly good performance for VIC integral form.

When performing the error computations for higher than 1000 with uniform mesh refinement of 2, 4, ...elements failure of computations occurs when dominates the total as expected.

6.2.3. LSP: Higher Order System (Without Auxiliary Equation)

In this study, we consider 1D convection-diffusion equation (124) without converting it to a system of first order equations through the use of auxiliary equation. In this case, is minimally conforming approximation space if the integrals over are to be Riemann. For the integrals over are Lebesgue and (solutions of class) is not admissible.

Error norms are computed for progressively refined uniform discretizations for (solutions of classes and) at p-levels of 3 and 5 for and and 7 for. Plots of error norms versus dof for

Figure 16. versus log(dofs) for solutions of class (GM/WF, model problem 2, ,).

Figure 17. versus log(dofs) for solutions of class (GM/WF, model problem 2, ,).

solutions of classes and and the calculated convergence rates and comparisons with the theoretical values are shown in Figure 18 and Figure 19. We note that the highest order of the derivative in the mathematical model () in this case is 2 as the convection-diffusion equation is not reduced to a first order system using auxiliary equations. Theoretical convergence rates are overall in good agreement with the calculated convergence rates confirming importance of the variational consistency of the integral form. In solutions of both classes, the convergence rate of is higher than predicted for. In this case whereas in case of first order system derived using auxiliary equation, thus the first order system has higher convergence rate of in the LSP.

Figure 20 shows plots of versus dofs and versus dofs for solutions of classes and at. Since the highest order derivative is two in the differential operator, the convergence rate of is same as that of. and solutions have same convergence rates but solutions have better accuracy for a given dofs, confirming that the convergence rates of error norm and residual functional are not a function of the order k of the approximation space. Thus, for higher order system we also observe that the rates for LSP match with GM/WF for self adjoint operators due to the fact that in both the integral forms are VC even though the two methods of approximation have best approximation property in different norms.

6.3. Model Problem 3: Non-Linear Operator, 1D Burgers Equation

We consider 1D Burgers equation described by a non-linear operator (see reference [35] ) to compute a priori error estimates and convergence rates of various error norms and compare them with their theoretical values,

(138)

(139)

For the studies presented in the following sections, a value of is used. Theoretical solution of

Figure 18. versus log(dofs) for solutions of class C¹ (LSP, model problem 2, higher order system, and 5,).

Figure 19. versus log(dofs) for solutions of class C² (LSP, model problem 2, higher order system, and 7,).

Figure 20. or versus log(dofs) for solutions of classes C¹ and C² at (LSP, higher order system, model problem 2).

(138) and (139) and finite element solution using GM/WF and LSP (higher order and first order systems) are given in reference [35] . Some details are given in the following as a review. It is shown [35] that in this case

which is a function of, hence non-linear. The GM/WF yields VIC integral form. The in-

tegral form from the LSP is VC with minor adjustments (see theorem 7) of little consequence but immense benefit as they yield variational consistency of the integral form.

a) GM/WF: The integral form of (138) and (139) over is given by

(140)

or

(141)

Functional is linear in v but not linear in and is obviously not symmetric.

(142)

is obviously not, , or , hence the integral form (141) is VIC.

b) LSP based on residual functional: These can be constructed in two alternate ways, as a higher order system (138) or by recasting (138) as a system of first order equations. [(I)]

I) Higher order system

(143)

and residual functional is given by

(144)

(145)

(146)

The necessary condition is satisfied by calculating a solution using Newton’s linear method. See reference [35] for full details. The integral form in this case is variationally consistent.

II) First order system

Let, then (138) reduces to

(147)

LSP for (147) is described in detail in reference [35] and is omitted here. This integral form is also VC.

6.3.1. LSP: Higher-Order System (Without Auxiliary Equation)

For this model problem we only present studies related to convergence rates of various error norms using (138) (i.e. without recasting it as a system of first order equations). As in other problems is discretized using uniform meshes of 2, 4, 8, ...3-node p-version higher order global differentiability elements and the solutions are computed using finite element formulations based on GM/WF and LSP. In case of LSP, since the integral form is VC the same convergence rate estimates hold as in (135):

(148)

In this BVP,. Since the differential operator has derivative of up to second order, the minimally conforming space in this case is for the integrals over to be Riemann and the integrals are in Lebesgue sense when. is not admissible. Figure 21 and Figure 22 show plots of various error norms versus dofs for solutions of class and as well as calculated and theoretical convergence rates.

First, we note from Figure 21 and Figure 22 large pre-asymptotic and onset of asymptotic ranges. The asymptotic range is rather limited, due to which accurate computation of convergence rates is difficult. Nonetheless we observe that for most error norms the theoretical and calculated convergence rates are in good agreement. Once again, we observe that due to VC integral form in LSP for nonlinear operators the convergence rate estimates for GM/WF for self adjoint operators and the same for LSP for linear operators hold here, again confirming the significance and importance of VC integral forms.

Figure 23 shows plots of versus dof and versus dof for solutions of class and at. Since the differential operator is second order operator, the convergence rate of is same as that of for both and local approximations. However, solutions have better accuracy for a given dofs. We clearly observe that the convergence rate is not a function of k, the order of approximation space. Calculated convergence rates of and are the same and are in exact agreement with the theoretical convergence rates.

6.3.2. GM/WF

Since the differential operator is non-linear the integral form from GM/WF is VIC. is not bilinear and is

Figure 21. versus log(dofs) for solutions of class C¹ (LSP, model problem 3, higher order system, and 5,).

Figure 22. versus log(dofs) for solutions of class C² (LSP, model problem 3, higher order system, and 7,).

Figure 23. or versus log(dofs) for solutions of classes C¹ and C² at (LSP, higher order system, model problem 3).

not symmetric, hence we lose best approximation property of the GM/WF in -norm. GM/WF will yield the following form of the assembled equations for (when and B) assuming uniform discretization ():

(149)

in which and. is symmetric. is due to and is due to term in the differential equation. Furthermore has zeros on the diagonal after

and boundary conditions are imposed, thus if is large, the contribution of to is almost insignificant and the computations using (149) will fail. On the other hand if the discretization is sufficiently refined then contribution of to overshadows that of and the solution behavior

will be dominated by (i.e. term in the differential equation). When this happens the integral form

from GM/WF will behave like a VC integral form and the convergence rates of various error norms will be same as those of GM/WF for self adjoint operator.

For numerical studies, we consider. Uniform mesh refinement is carried out for solutions of class at. Figure 24 shows plots of error norms versus dofs. We note that for discretizations coarser than 128 elements the error norms correspond to erroneous computed solutions in which equilibrium condition is violated for the assembled equations. For finer discretizations (128 elements or more) asymptotic range is observed. In this range discretization is sufficiently refined so that the integral form is dominated by the diffusion term. Calculated convergence rates (of;,;,) 3.7, 3, and 2 are in close agreement with the theoretical convergence rates 4, 3, 2. In this study for computations failed for discretizations coarser than 128 elements where equilibrium was not achieved.

Figure 24. versus log(dofs) for solutions of class C¹ (GM/WF, model problem 3, p = 3,).

7. A Posteriori Error Estimation and Computation

7.1. A Posteriori Error Estimation

A posteriori error estimation refers to estimation of errors in the computed solution. The primary purpose is to be able to devise some element-wise measures as well as in the whole discretization that quantify the errors in the computed solution as well as provide some guidance on the portions of the domain where the computed solution needs to be improved. Based on these measures one could design mesh refinement, p-level change, etc. strategies that result in the desired accuracy of the computed solution. This process of changing h, p, and possibly k based on measures estimated using the computed solution is referred to as adaptive process (i.e. we adapt h, p, and k as dictated by the current state of the solution and a posteriori error estimators or indicators).

During the development of finite element technology and even now, solutions of class have been used predominantly. The local approximations of class result in interelement discontinuity of the derivatives normal to the interelement boundaries. When the solutions of the BVPs are smooth, these interelement jumps in the derivatives are reduced upon h, p refinements and we say solutions converge weakly to class. The a posteriori error estimations largely exploit the interelement discontinuities of the derivatives inherent in local approximations. We note the following.

1) When the local approximations are considered in higher order spaces, the a posteriori error estimates used currently that are derived based on local approximations are meaningless as for higher order global differentiability local approximations the interelement jumps in the derivatives of the solutions used currently do not exist.

2) The local approximations can only be used in a system of first order differential equations to calculate the residuals and residual functionals over as well as over, but only in Lebesgue sense. For higher order BVPs such computations are not possible with local approximations of class. Even though the residual functional over and are true measures of how well the local approximation satisfies the BVP, the emphasis has been largely on a posteriori error estimation, primarily due to the insistence on the use of local approximations.

3) Our view is that in a finite element computational framework the physics of the BVP must be preserved and in such a framework, once a finite element solution has been calculated, the computational framework must permit a posteriori computations of any desired measures otherwise the computational framework is deficient.

7.2. A Posteriori Error Computation

As mentioned in Section 7.1, the computational framework must be designed such that it permits a posteriori computations of all desired measures that are necessary and meaningful in adaptivity. Minimally conforming spaces play a crucial role in accomplishing this. We present details in the following. Let

(150)

be a boundary value problem in which the differential operator may be self adjoint, non-self adjoint, or non- linear. Let be the highest order of the derivative of in (150). Let and be approximations of over and. The approximation is assumed to be computed from any of the methods of approximation in which the integral forms may be VC or VIC. Let

(151)

(152)

The approximation space is minimally conforming ensuring that the integrals over are Riemann. Using (150) and (152), we can define residual functions

(153)

where n is the number of differential equations in (150). Let

(154)

We define residual functionals I and over and by

(155)

(156)

Since, we can write (using (155) and (156))

(157)

If is the theoretical solution then

(158)

and

(159)

over and each. Minimally conforming space ensures that integrals over are Riemann, hence proximity of to zero (theoretical value of functional I; that is,) is a measure of error in the solution over. When, , thus for each in, implying that differential Equation (150) are satisfied in the pointwise sense. Thus, the main steps in a posteriori error computation can be summarized in the following.

1) Choose minimally conforming space thereby ensuring integrals over in Riemann sense.

2) Regardless of the method of approximation to construct integral form in the finite element process, the following steps are possible and help in quantifying solution error. Calculate finite element solution and hence.

3) Calculate, for each element e with domain of the discretization.

4) Calculate for.

5) When (or lower), is reasonably converged to for the h, p, and k employed, hence no need for adaptive refinements.

6) When, we examine values for individual elements of to determine which elements have values larger than a certain threshold value. These elements can be considered for adaptive refinement (h or p or both) depending on the strategy adopted. Some of these are presented in the next section.

7) In this approach, a posteriori error estimations derived and used presently (of little value in higher order spaces) are eliminated altogether.

8) Errors in the computed solution are quantified without the knowledge of theoretical solution and there is built-in adaptivity due to for individual elements. The elements with values larger than a threshold value are candidates for refinement.

9) Adaptive processes based on values for elements of descretization are presented in the next section.

8. Summary and Conclusions

In this paper, we have considered a priori and a posteriori error estimations, a posteriori error computation, and convergence rates of the finite element computations for BVPs described by self-adjoint, non-self-adjoint, and nonlinear differential operators. Concepts of h-, p-, and k-versions and h-, p-, and k-convergences in finite element processes are presented and discussed. It is shown that a desired measure of error norm or residual functional versus degrees of freedom behavior has distinct features that can be classified as pre-asymptotic range, onset of asymptotic range, asymptotic range, onset of post-asymptotic range, and post-asymptotic range. The significance and importance of these ranges in finite element computations has been discussed and demonstrated through three model problems described by self adjoint, non-self adjoint, and non-linear differential operators.

The a priori estimates only hold in asymptotic range and their derivation in the currently published literature are only valid for self adjoint operators in GM/WF when functional is symmetric, thus GM/WF has best approximation property in B-norm. New work presented in this paper establishes correspondence between best approximation property of an integral form in some norm and the variational consistency of the integral form and demonstrates that when one exists the other is ensured. Thus, for establishing a priori error estimates, variational consistency becomes an essential property of the integral form. Of course best approximation property in some norm if it exists is equally good as best approximation property and variational consistency of integral form can not exist without each other, i.e. they co-exist. In case of GM/WF, VC integral form is possible for self adjoint operator and in case of LSP VC integral form is possible for all three classes of differential operators, hence a priori estimates for GM/WF for self adjoint operators and a priori estimates for LSP for all three classes of operators can be derived. The derivation of a priori error estimates presented in proposition 5.2 applies to GM/WF for self adjoint operators and in case of LSP for all three classes of operators as well as any other integral form resulting from a chosen method of approximation as long as the integral form is VC. Numerical studies for the model problems containing the three classes of operators confirm that when the integral form is VC, same a priori estimates and convergence rates hold. Thus, for the first time we have a priori error estimates for non-self adjoint and non-linear differential operators. Extensive numerical studies are presented for various p and k values for uniform h-refinements demonstrating that the theoretically derived convergence rates in a priori estimates are always in agreement with calculated values when the integral forms are VC. The a priori error estimates derived here also hold for 2D and 3D BVPs as long as the integral forms in these BVPs are variationally consistent. This can be confirmed numerically and is in agreement with published literature for self adjoint operators.

A posteriori error estimation based on the work presented here is viewed unnecessary when the approximation spaces are minimally conforming or of orders higher than minimally conforming due to the fact that when using such spaces a posteriori error computations of any desired quantity (for example and I) that can help guide adaptivity is possible. residual values for elements of are shown to be a perfect choice for adaptivity.

In short, VC integral form permits derivation of a priori error estimates and determination of convergence rates for all three classes of differential operators and use of minimally conforming spaces make a posteriori error estimation unnecessary and permit determination of desired a posteriori measures (such as and I) that can be used to quantify errors in the currently computed solution and to design adaptive processes (presented in a followup paper). The same estimates and convergence rates hold for 2D and 3D BVPs when the integral forms are VC. The details are somewhat involved and have been presented in published literature for self-adjoint operators.

Acknowledgments

The first and third authors are grateful for the support provided by their endowed professorships during the course of this research. The computational infrastructure provided by the Computational Mechanics Laboratory (CML) of the Mechanical Engineering department of the University of Kansas is gratefully acknowledged. The financial support provided to the second author by the Naval Air Warfare Center is greatly appreciated.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Surana, K.S., Ahmadi, A.R. and Reddy, J.N. (2002) The k-Version of Finite Element Method for Self-Adjoint Operators in BVP. International Journal of Computational Engineering Science, 3, 155-218. http://dx.doi.org/10.1142/S1465876302000605
[2]	Surana, K.S., Ahmadi, A.R. and Reddy, J.N. (2003) The k-Version of Finite Element Method for Non-Self-Adjoint Operators in BVP. International Journal of Computational Engineering Science, 4, 737-812. http://dx.doi.org/10.1142/S1465876303002179
[3]	Surana, K.S., Ahmadi, A.R. and Reddy, J.N. (2004) The k-Version of Finite Element Method for Non-Linear Operators in BVP. International Journal of Computational Engineering Science, 5, 133-207. http://dx.doi.org/10.1142/S1465876304002307
[4]	Surana, K.S., Allu, S. and Reddy, J.N. (2007) The k-Version of Finite Element Method for Initial Value Problems: Mathematical and Computational Framework. International Journal of Computational Engineering Science, 8, 123-136. http://dx.doi.org/10.1080/15502280701252321
[5]	Babuska, I. and Rheinboldt, W.C. (1978) A Posteriori Error Estimates for the Finite Element Method. International Journal for Numerical Methods in Engineering, 12, 1597-1615. http://dx.doi.org/10.1002/nme.1620121010
[6]	Babuska, I. and Rheinboldt, W.C. (1978) Error Estimates for Adaptive Finite Element Computations. SIAM Journal on Numerical Analysis, 18, 736-754. http://dx.doi.org/10.1137/0715049
[7]	Babuska, I. and Rheinboldt, W.C. (1979) Adaptive Approaches and Reliability Estimations in Finite Element Analysis. Computer Methods in Applied Mechanics and Engineering, 17, 519-540. http://dx.doi.org/10.1016/0045-7825(79)90042-2
[8]	Babuska, I. and Rheinboldt, W.C. (1981) A Posteriori Error Analysis of Finite Element Solutions for One Dimensional Problems. SIAM Journal on Numerical Analysis, 18, 435-463. http://dx.doi.org/10.1137/0718036
[9]	Ainsworth, M. and Oden, J.T. (2000) A Posteriori Error Estimation in Finite Element Analysis. Wiley-Interscience, Hoboken.
[10]	Szabo, B.A. and Babuska, I. (1991) Finite Element Analysis. Wiley-Interscience, Hoboken.
[11]	Schwab, Ch. (1998) p and hp Finite Element Methods. Clarendon Press, Oxford.
[12]	Guo, G. and Babuska, I. (1986) The hp Version of the Finite Element Method. Part 1: The Basic Approximation Results. Part 2: General Results and Applications. Computational Mechanics, 1, 21-41, 203-220.
[13]	Gui, W. and Babuska, I. (1986) The h, p and hp Versions of the Finite Element Method in One Dimension. Part 1: The Error Analysis of the p-Version. Part 2: The Error Analysis of the h- and hp-Versions. Part 3: The Adptive hp-Versions. Numerische Mathematik, 49, 577-683. http://dx.doi.org/10.1007/BF01389733
[14]	Ainsworth, M. and Senior, B. (1997) An Adaptive Refinement Strategy for hp-Finite Element Computations. Applied Numerical Mathematics, 26, 165-178. http://dx.doi.org/10.1016/S0168-9274(97)00083-4
[15]	Oden, J.T., Patra, A. and Feng, Y. (1992) An hp Adaptive Strategy. In Noor, A.K., Ed., Adaptive Multilevel and Hierarchical Computational Strategies, ASME Publication, 23-46.
[16]	Rachowicz, W. (1989) An hp Finite Element Method for One-Irregular Meshes, Error Estimation and Mesh Refinement Strategy. PhD Thesis, University of Texas at Austin, Austin.
[17]	Demkowicz, L. (2007) Computing with hp-Adaptive Finite Elements. Chapman and Hall/CRC, Boca Raton.
[18]	Babuska, I. and Strouboulis, T. (2001) The Finite Element Method and Its Reliability. Oxford University Press Inc., New York.
[19]	Jiang, B. (1998) The Least-Squares Finite Element Method: Theory and Applications in Computational Fluid Dynamics and Electromagnetics. Springer, Berlin. http://dx.doi.org/10.1007/978-3-662-03740-9
[20]	Strouboulis, T. and Haque, K.A. (1992) Recent Experiences with Error Estimation and Adaptivity. Part I: Review of Error Estimators for Scalar Elliptic Problems. Computer Methods in Applied Mechanics and Engineering, 97, 399-436. http://dx.doi.org/10.1016/0045-7825(92)90053-M
[21]	Strouboulis, T. and Haque, K.A. (1992) Recent Experiences with Error Estimation and Adaptivity. Part II: Error Estimation for h-adaptive Approximations on Grids of Triangles and Quadrilaterals. Computer Methods in Applied Mechanics and Engineering, 100, 359-430. http://dx.doi.org/10.1016/0045-7825(92)90090-7
[22]	Apel, T. (1999) Anisoptropic Finite Elements: Local Estimates and Applications. Teubner.
[23]	Surana, K.S., Stone, T., Reddy, J.N. and Romkes, A. (2011) Adaptivity in hpk Finite Element Processes. Proceedings of the 11th US Congress on Computational Mechanics (USNCCM-11), Minneapolis, 25-28 July 2011.
[24]	Surana, K.S., Stone, T., Romkes, A. and Reddy, J.N. (2009) Adaptivity in Finite Element Processes in hpk Mathematical and Computational Framework. Proceedings of the 10th US Congress on Computational Mechanics (USNCCM-10), Columbus, 15-19 July 2009.
[25]	Romkes, A., Bryant, C.M. and Reddy, J.N. (2010) A Posteriori Error Estimation of hpk FE Solutions of Linear Boundary Value Problems in Terms of Quantities of Interest. Proceedings of the International Conference on Multiscale Modeling and Simulation (ICMMS-2010), Guangzhou, 17-19 December 2010.
[26]	Surana, K.S., Stone, T., Romkes, A. and Reddy, J.N. (2009) Adaptivity in Finite Element Processes in hpk Mathematical and Computational Framework. Proceedings of the ICCMES, Hyderabad, 8-10 January 2009.
[27]	Romkes, A., Surana, K.S., Reddy, J.N. and Stone, T. (2008) Error Estimation for the K-Version of the Finite Element Method. Proceedings of the International Conference on Multiscale Modeling and Simulation (ICMMS-2008), Bangalore, 2-4 January 2008.
[28]	Romkes, A., Reddy, J.N., Stone, T. and Surana, K.S. (2007) A Priori Error Estimation in hpk FE Analysis. Proceedings of the 9th US Congress on Computational Mechanics (USNCCM-9), San Francisco, 22-26 July 2007.
[29]	Reddy, J.N. (2006) An Introduction to the Finite Element Method. 3rd Edition, McGraw Hill Inc., New York.
[30]	Claes J. (1994) Numerical Solutions of Partial Differential Equations. Cambridge University Press, New York.
[31]	White, R.E. (1985) An Introduction to the Finite Element Method with Applications to Nonlinear Problems. John Wiley & Sons, New York.
[32]	Carey, G.F. and Oden J.T. (1983) Finite Elements: A Second Course, Volume II. Prentice Hall, Upper Saddle River.
[33]	Oden, J.T. and Carey, G.F. (1983) Finite Elements: Mathematical Aspects. Prentice Hall, Upper Saddle River.
[34]	Reddy, J.N. (1986) Applied Functional Analysis and Variational Methods in Engineering. McGraw Hill Company, New York.
[35]	Surana, K.S. and Reddy, J.N. (2016) The Finite Element Method for Boundary Value Problems: Mathematics and Computations. CRC/Taylor and Francis, London. (In Press)