Received 25 May 2016; accepted 25 July 2016; published 28 July 2016

1. Introduction
For the Burgers-Huxley equation
 (1)
(1)
This an important equation used to describe the nonlinear diffusion phenomenon. In recent years, with the development of Symbolic Computation System and its perfection, people put forward a number of methods for solving the nonlinear equations of mathematical physics, such as the homogeneous balance method, F-method, Tanh method, projective Riccati method, ADM method [1] - [4] and bifurcation theory to direct integral method [5] and so on. G'/G expansion method [6] is proposed for solving nonlinear evolution equation and provided an effective method. This method has effectively solved many nonlinear evolution equations.
This article will make the G'/G expansion method extended further, solving the Burger-Huxley equation [7] - [10] and two kinds of special transformations.
2. The Introduction of Extended G'/G-Expansion Method [11] [12]
Given nonlinear PDE, containing two independent variables x and t:
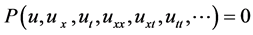 (2)
(2)
Among them, P is the polynomial of variable element u with high order partial derivative term and nonlinear term. For equations by G'/G expansion method (2) comprises the following steps:
1) On Equation (2) traveling wave reduction, let
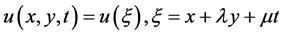 (3)
(3)
Among them,  and
and  are undetermined constants. Equation (3) is plugged into Equation (2). (ODE type):
are undetermined constants. Equation (3) is plugged into Equation (2). (ODE type):
 (4)
(4)
2) The 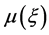 can be expressed as the finite series of G'/G
can be expressed as the finite series of G'/G
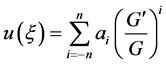 (5)
(5)
The 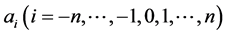 is a undetermined constant; the
is a undetermined constant; the  meet the two order linear ordinary differential equation as follows
meet the two order linear ordinary differential equation as follows
 (6)
(6)
The positive integer n can be determined by the balance principle homogeneous.
3) We will plug Equation (5) into Equation (4), then the left of Equation (4) translates the polynomial of G'/G, making this polynomial coefficients are all zero, can obtain the algebraic equations about
 .
.
4) With the help of Mathematica, we can solve the algebraic equations. so we can obtain the exact traveling wave solutions of Equation (1) that plugging the resulting value of  into Equation (4) [13] [14] .
into Equation (4) [13] [14] .
3. Calculate the Exact Solution of the Burger-Huxley Equation [15]
Make Burger-Huxley Equation for wave reduction, let
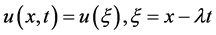 (7)
(7)
so Equation (1) can translate the ODE equation;
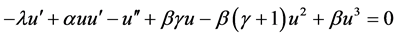 (8)
(8)
We can obtain a series of expansion of n is 1, assuming Equation (8) has the following form solution:
![]() (9)
(9)
Among them, ![]() meet the two order linear ordinary differential equation (LODE) equation
meet the two order linear ordinary differential equation (LODE) equation
![]() (10)
(10)
In Equation (9) and Equation (10), ![]() are the undetermined coefficients, according to the two equations, we can obtain relation as follows:
are the undetermined coefficients, according to the two equations, we can obtain relation as follows:
![]() (11)
(11)
Plugging Equation (11) into Equation (8), Equation (8) can be transformed into a polynomial about G'/G expansion. Merger these items with respect to G'/G expansion which have the same power, and its coefficient is zero. We can obtain the equations as follows.
![]() (12)
(12)
If set ![]() to undetermined constants, with the help of Mathematica software, we can get the values of
to undetermined constants, with the help of Mathematica software, we can get the values of ![]() as follows:
as follows:
1)![]()
![]()
![]() ,
, ![]()
2)
![]()
![]()
![]() ,
,![]() (13)
(13)
By using mathematics software to calculate again, a general solution of Equation (10) can be represented as:
![]() (14)
(14)
Substituting Equation (13) and Equation (14) into Equation (9), traveling wave solution of Equation (1) can be obtained:
1) When![]() ,
,
![]()
![]()
where![]() ;
;
2) When![]() ,
,
![]()
![]()
where![]() ;
;
3) When![]() ,
,
![]()
![]()
where![]() .
.
When the original equation of the parameters in the ![]() take different values, we can get different kinds of evolution equations, here are the two special forms to continue the discussion.
take different values, we can get different kinds of evolution equations, here are the two special forms to continue the discussion.
Case 1: when![]() , the equation is Fitz Hugh-Nagumo equation, so Equation (8) turns into:
, the equation is Fitz Hugh-Nagumo equation, so Equation (8) turns into:
![]() (15)
(15)
We assume that the same G'/G expression, by substitution to Equation (15) to obtain the following equations:
![]() (16)
(16)
With the aid of Mathematica software, we can get the value of ![]() are as follows:
are as follows:
1) ![]()
2) ![]()
3)
![]() (17)
(17)
Equation (15) can be expressed as the solution:
1) When![]() ,
,
![]()
![]()
![]()
where![]() ;
;
2) When![]() ,
,
![]()
![]()
![]()
where![]() ;
;
3) When![]() ,
,
![]()
![]()
![]()
where![]() .
.
Case 2: when![]() , Equation (1) can translate into the Burgers equation
, Equation (1) can translate into the Burgers equation
![]() (18)
(18)
Make the equation to traveling wave reduced, let![]() ,so Equation (18) can translate the NODE equation;
,so Equation (18) can translate the NODE equation;
![]() (19)
(19)
Make Equation (19) to integral, so
![]() (20)
(20)
We assume that the same G'/G expression, through to obtain the following equations
![]() (21)
(21)
With the aid of mathematica software, obtain the solution of the following:
![]() (exclude
(exclude![]() )
)
so the solution of Equation (18) can be expressed:
![]() (22)
(22)
Including to Equation (15), we can obtain the accurate solution of Equation (18):
1) When![]() ,
,
![]()
where![]() ;
;
2) When![]() ,
,
![]()
where![]() ;
;
3) When![]() ,
,
![]()
where![]() .
.
4. Conclusion
Based on the homogeneous balance method, the article obtains solutions of the Burgers-Huxley equation and two kinds of transformation type by the G'/G expansion method, making the Burgers-Huxley equation and its derivative equation solution in the form of more abundant. At the same time, we can obtain the hyperbolic traveling wave solutions of the equation and find the G'/G expansion method [16] in solving nonlinear evolution equations has very extensive practical value.