Loops in Digraphs of Lambert Mapping Modulo Prime Powers: Enumerations and Applications ()
Received 5 February 2016; accepted 25 July 2016; published 28 July 2016

1. Introduction
The Lambert W functions are used to find solutions of such equations in which the unknown also appears in
exponential (or logarithmic) terms. It is defined as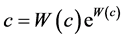 , where c is a complex number. Equivalently, it can be defined as
, where c is a complex number. Equivalently, it can be defined as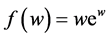 . Lambert solved a Diophantine equation
. Lambert solved a Diophantine equation 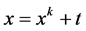 in 1758 (see [1] ). Later,
in 1758 (see [1] ). Later,
the solution is expressed in term of series. In 1980, the Lambert function was stored in MCAS (Maple Computer Algebra System) as a function for the solution of algebraic equations involving exponential (or logarithmic) functions (see [2] ). In this work, we discussed solutions of such functions by means of their digraphs using residue theory from number theory.
Let ![]() be the ring of residue classes modulo
be the ring of residue classes modulo![]() . Define
. Define ![]() by
by![]() , the discrete Lambert mapping, where
, the discrete Lambert mapping, where![]() . We investigate this mapping using directed graphs whose vertices are residues modulo
. We investigate this mapping using directed graphs whose vertices are residues modulo ![]() with edges from
with edges from ![]() to
to ![]() if and only if
if and only if![]() . This digraph is denoted by
. This digraph is denoted by![]() .
.
We investigate self loops (fixed points) of these digraphs and also lift up the investigations of such digraphs by Jingjing Chen and Mark Lotts in [3] from modulo a prime p to modulo![]() . Results regarding fixed points, isolated points followed by astute proofs have been presented. It is important to note that all solutions of congruences of Lambert functions are difficult to find since such mappings are hard to invert and need enormous inversions in any computer algorithm. To understand the terminology and symbols, we follow [3] - [6] .
. Results regarding fixed points, isolated points followed by astute proofs have been presented. It is important to note that all solutions of congruences of Lambert functions are difficult to find since such mappings are hard to invert and need enormous inversions in any computer algorithm. To understand the terminology and symbols, we follow [3] - [6] .
Definition 1. (see [7] ). Let p be prime and a be any integer not divisible by p. A least positive integer r such that ![]() is called order of a modulo
is called order of a modulo![]() . It is denoted as
. It is denoted as![]() .
.
Theorem 0. (see [3] ). Let q be any prime and![]() . Then,
. Then,
1. Let g be a quadratic residue of q, then![]() .
.
2. A point t is fixed Û![]() .
.
3. Fixed points of f are multiples of the order of g.
4. Let![]() . If t is odd, then
. If t is odd, then![]() , and if t is even, then
, and if t is even, then ![]() is a fixed point.
is a fixed point.
Let’s draw a digraph of the Lambert map. Take ![]() and chose a composite modulus m as
and chose a composite modulus m as![]() . We see that the digraph (see Figure 1) has six loops (fixed points) of which three are non-isolated. The digraph has two non-isomorphic components.
. We see that the digraph (see Figure 1) has six loops (fixed points) of which three are non-isolated. The digraph has two non-isomorphic components.
2. Fixed Points of the Map
Recall that a vertex u is said to have a loop ( fixed point) on it if ![]() and it referred to as an isolated fixed point of the graph
and it referred to as an isolated fixed point of the graph ![]() if
if ![]() and there does not exist any vertex v such that
and there does not exist any vertex v such that![]() . In this section, we present some results to find fixed points (or loops) and isolated points of the graph
. In this section, we present some results to find fixed points (or loops) and isolated points of the graph![]() .
.
Lemma 1. Let p be any prime. Then, ![]() if and only if
if and only if ![]() for any integer g.
for any integer g.
Proof. Let![]() . Then 2 is the least positive integer such that
. Then 2 is the least positive integer such that![]() . This means that either
. This means that either ![]() or
or![]() . But the first implies that,
. But the first implies that,![]() . Hence
. Hence![]() . Since
. Since![]() . Thus
. Thus![]() . Conversely, it is easy to see that
. Conversely, it is easy to see that![]() .
.
,
The proof of the following theorem is simple and can be established similar to Theorem 0 (4).
Theorem 1. Let ![]() and f be Discrete Lambert Map. If a is any odd residue of
and f be Discrete Lambert Map. If a is any odd residue of ![]() then
then ![]() and if a is an even residue of
and if a is an even residue of ![]() then
then ![]() under f.
under f.
In the following theorem, we find the values of g for which the fixed points of the digraph are necessarily isolated. Before proving the assertion, we give the following important lemmas.
Lemma 2. If ![]() then
then ![]() are the fixed points of the graph
are the fixed points of the graph![]() . In particular, the vertices,
. In particular, the vertices, ![]() when k is odd and
when k is odd and ![]() when k is even are always fixed points.
when k is even are always fixed points.
Proof. Let![]() , then
, then ![]() for some integer s. But then
for some integer s. But then
![]() (1)
(1)
For the rest of the proof, we note that ![]() when k is odd and
when k is odd and ![]() when k is even. Therefore,
when k is even. Therefore,
![]()
The case when k is odd can be dealt in a similar technique. ,
The following Lemma is of crucial importance. However, its proof is simple and can be viewed as a direct consequence of the Definition 1.
Lemma 3. Let g be a residue of![]() . Then
. Then ![]() if and only if
if and only if ![]()
Proof. Let![]() . Then l is the least positive integer such that
. Then l is the least positive integer such that![]() . Suppose
. Suppose![]() , then
, then ![]() for some integer s such that
for some integer s such that ![]() and
and![]() . Now
. Now
![]()
Thus ![]() if and only if
if and only if![]() . But
. But![]() . Hence, we conclude that
. Hence, we conclude that ![]() for
for![]() . ,
. ,
Lemma 4. Let![]() . If
. If ![]() divides v then v is a fixed point of the digraph
divides v then v is a fixed point of the digraph![]() .
.
Proof. Let![]() . Then
. Then ![]() is the least positive integer such that
is the least positive integer such that![]() . Now for any vertex v, if
. Now for any vertex v, if ![]() divides v then
divides v then ![]() for some integer
for some integer![]() . But then
. But then![]() . ,
. ,
Theorem 2. If![]() , then all fixed points of
, then all fixed points of ![]() are isolated.
are isolated.
Proof. Let![]() . Then by Lemma 3,
. Then by Lemma 3, ![]() for
for![]() . This means that possible orders of g modulo
. This means that possible orders of g modulo ![]() are
are![]() . Hence by Lemma 4,
. Hence by Lemma 4, ![]() , for any integer
, for any integer![]() , are the fixed points. We need only to show that these are the possible fixed points and are isolated. Since
, are the fixed points. We need only to show that these are the possible fixed points and are isolated. Since![]() , so,
, so, ![]() , where
, where ![]() and
and![]() . Let x be any fixed point in
. Let x be any fixed point in![]() , then
, then![]() . Or
. Or
![]() . This means that either
. This means that either ![]() or
or![]() . But
. But![]() . Hence
. Hence ![]() . This clearly shows that x is
. This clearly shows that x is ![]() or multiple of
or multiple of![]() . Finally, we show that these are isolated. Let
. Finally, we show that these are isolated. Let ![]() for some
for some![]() , is adjacent to some
, is adjacent to some![]() . Then
. Then![]() . But
. But ![]() , so
, so ![]() implies that
implies that![]() . That is,
. That is, ![]() , which is not possible since
, which is not possible since ![]() ,
,
Figure 2 depicts Theorems 2 and 3. In Figure 2, we note that![]() . By Theorem 2, the vertices 5, 10, 15, 20 are the fixed points and are isolated. Also
. By Theorem 2, the vertices 5, 10, 15, 20 are the fixed points and are isolated. Also ![]() is not a multiple of 5, so by Theorem 3, 0 is also an isolated fixed point. Thus all fixed points are isolated.
is not a multiple of 5, so by Theorem 3, 0 is also an isolated fixed point. Thus all fixed points are isolated.
Theorem 3. Let ![]() be a discrete Lambert digraph. Then,
be a discrete Lambert digraph. Then,
i) If ![]() then 0 is the only fixed point of G.
then 0 is the only fixed point of G.
ii) 0 is an isolated fixed point of G if and only if ![]()
iii) If ![]() is a fixed point then
is a fixed point then ![]()
Proof. i) Let ![]() and x be any fixed point of G. Then,
and x be any fixed point of G. Then,
![]() (2)
(2)
This means that either ![]() or
or![]() . But
. But![]() , so
, so![]() . Hence (2) yields that,
. Hence (2) yields that, ![]() . This is possible only if
. This is possible only if![]() .
.
ii) Let ![]() On contrary we suppose that there exist a vertex
On contrary we suppose that there exist a vertex ![]() such that x is adjacent to 0. That is,
such that x is adjacent to 0. That is,![]() . This means that
. This means that![]() . But
. But![]() . Hence,
. Hence,
![]() . This certainly implies that
. This certainly implies that![]() . Hence,
. Hence, ![]() for some integer k, a contradiction to supposition that
for some integer k, a contradiction to supposition that![]() . Hence 0 is isolated.
. Hence 0 is isolated.
Conversely, suppose 0 is isolated. Let there be any integer k such that ![]() and there exist some x such that
and there exist some x such that![]() . Then there must exist some integer
. Then there must exist some integer ![]() such that
such that![]() . This shows that 0 is not isolated, a contradiction. Therefore
. This shows that 0 is not isolated, a contradiction. Therefore![]() .
.
iii) Let ![]() be a fixed point together with
be a fixed point together with ![]() Then,
Then,
![]()
![]()
This shows that ![]() is a primitive root of
is a primitive root of![]() . But
. But![]() . Thus the word primitive root arrive at a contradiction. ,
. Thus the word primitive root arrive at a contradiction. ,
The following corollaries are the simple consequences of above theorem.
Corollary 1. Let ![]() be the set of vertices in
be the set of vertices in![]() . If
. If ![]() then the digraph
then the digraph ![]() has no fixed point.
has no fixed point.
Corollary 2. If ![]() then
then ![]() is not a fixed point.
is not a fixed point.
Theorem 4. The digraph ![]() contains no cycles except fixed points if and only if either g is of order 2 or g is divisible by p.
contains no cycles except fixed points if and only if either g is of order 2 or g is divisible by p.
Proof. By Lemma 1, ![]() if and only if
if and only if ![]() for any integer g. Also by Theorem 1, if
for any integer g. Also by Theorem 1, if ![]() and x is odd then
and x is odd then ![]() otherwise
otherwise![]() . We claim that there exist no cycle of length 2. For otherwise, an odd vertex a must mapped onto
. We claim that there exist no cycle of length 2. For otherwise, an odd vertex a must mapped onto ![]() (say), which is of course even and hence b can never adjacent to a since
(say), which is of course even and hence b can never adjacent to a since![]() , being even, a contradiction. Thus there does not exist any cycle of length > 1. Now if g is a multiple of p then it is trivial that all vertices constitute one component. Also by Theorem 3(i), if g is a multiple of p then 0 is the only fixed point. Thus the digraph must be a tree with root at 0. Consequently
, being even, a contradiction. Thus there does not exist any cycle of length > 1. Now if g is a multiple of p then it is trivial that all vertices constitute one component. Also by Theorem 3(i), if g is a multiple of p then 0 is the only fixed point. Thus the digraph must be a tree with root at 0. Consequently ![]() contains no cycle of length > 1. ,
contains no cycle of length > 1. ,
In Figure 3,![]() . By Theorem 4, 0 is the only isolated fixed points.
. By Theorem 4, 0 is the only isolated fixed points.
3. Applications
In recent years, studying graphs through different structural environments like groups, rings, congruences has become much captivating and dominant field of discrete mathematics. These assignments are easy to handle most of the mathematics which is integral based. A variety of graphs have been introduced and characterized regarding their structures through this dynamism. By means of congruences one can inspect numerous enthralling topographies of graphs and digraphs. Thus it becomes interesting to demonstrate that every congruence can generate a graph and hence under certain conditions on these graphs, the nature and solutions of congruences can be discussed. In this section, we discuss the solvability of the congruence and enumerate their solutions using the results given in previous section. The non-trivial ( other than![]() ) solution of the congruence modulo a single prime p is easy to discuss since every
) solution of the congruence modulo a single prime p is easy to discuss since every ![]() is prime to p. So the congruence
is prime to p. So the congruence ![]() is solvable if and only if
is solvable if and only if ![]() as given in Theorem 0 (4). Hence by Fermat's Little Theorem, the number
as given in Theorem 0 (4). Hence by Fermat's Little Theorem, the number ![]() becomes a solution of
becomes a solution of![]() . Now if we lift up the modulo from p to its higher powers
. Now if we lift up the modulo from p to its higher powers![]() , then the vertices which are not prime to p must not follow the fashion as for
, then the vertices which are not prime to p must not follow the fashion as for![]() .
.
The following result tackle this case and enumerate the solutions as well. Note that the vertex ![]() is the trivial solution in either case. The proof of the following theorem is simple and can be established using results given in Section 2.
is the trivial solution in either case. The proof of the following theorem is simple and can be established using results given in Section 2.
Theorem 5. Let p be an odd prime and![]() . Then the following hold:
. Then the following hold:
1. If ![]() then the congruence
then the congruence ![]() is solvable.
is solvable.
2. Let ![]() be any integer. If
be any integer. If ![]() then the congruence
then the congruence ![]() is solvable.
is solvable.
In particular, ![]() all are its
all are its ![]() solutions.
solutions.
3. If g is a primitive root of ![]() then congruence
then congruence ![]() has a unique non-trivial solution.
has a unique non-trivial solution.
Thus, 0 and ![]() are the only solutions of
are the only solutions of![]() .
.
4. If![]() , then the congruence
, then the congruence ![]() has no non-trivial solution.
has no non-trivial solution.
Acknowledgements
We are very thankful to the editor and the reviewers for specially sparing their precious time and forwarding useful comments. We sincerely believe that this has made the manuscript more interesting and informative.