Heat Transfer during Spray Cooling of Flat Surfaces with Water at Large Reynolds Numbers ()
Received 1 March 2016; accepted 23 June 2016; published 27 July 2016

1. Introduction
Enhanced heat transfer is widely used in various industrial processes and devices, including gas-turbine combustor cooling, steel production and metal processing. Heat removal through cooling and evaporation of liquid (most commonly, water) sprays is an attractive method, due to large volumetric flow rate and heat capacity. The thermal performance during spray injection of liquid onto surfaces is normally represented by the associated heat transfer coefficient (HTC) or the Nusselt number, which is a measure of the cooling rate due to forced convection. Characterization of the heat transfer coefficient is important for determining the required cooling capacity and corresponding internal properties of the product. For this reason, a vast amount of work has been devoted to parameterize or model the heat transfer coefficient during spray cooling in different flow regimes [1] [2] .
In large majority of applications as well as in this work, the interest is in large volumetric-flow-rate spray cooling or large Reynolds numbers, and for hot surfaces above the so-called Leidenfrost temperature (TLei). Here, the Reynolds number is defined as the Re = ρUL/μ, where U is the mean injection velocity of water at the injector exit, L the length scale of the surface to be cooled, and ρ and μ the water density and viscosity, respectively. The injection velocity has been obtained by measuring the volumetric flow rate of water and dividing by the injector area. At these conditions, the flow is turbulent and the cooling occurs through film-boiling in which a stable vapor film exists at the hot surface. The turbulent two-phase flow and heat transfer in these regimes involve complex transport processes, with several more factors to consider than in single-phase heat transfer. The Leidenfrost temperature, for example, has been found to be dependent on the Weber number [2] and other spray parameters, and does not have a fixed value varying from 400˚C to 600˚C [3] [4] . The HTC in the film-boiling regime has also been considered to be temperature-independent with the heat flux (qh) linearly increasing with the surface temperature, Ts [5] . Since the surface temperature during secondary cooling (Figure 1) occurs over a wide range of temperature, approximately from 600˚C to higher than 1200˚C, the notion of the temperature-independent HTC, which is usually based on a relatively narrow range of testing temperature, can be in-
![]()
Figure 1. Schematic diagram of continuous casting of steel.
complete or misleading. For example, by considering Ts varying from 200˚C to 1100˚C, Wendelstorf [4] and Raudensky et al. [6] reported that the heat transfer coefficient in the stable film boiling regime decreased as Ts increased. Here, the logic is that the primary cooling effect comes from the flow rate, or the Reynolds number effect. Then, other effects such as boiling, void fraction and two-phase flow structure near the surface can be accounted for using fluid property changes and thermodynamic considerations.
An example of the application of spray cooling is the continuous casting, also called strand casting, which is currently the most efficient method for steel production. During continuous casting as shown in Figure 1, large volumes of molten metal are solidified into simple shapes of semi-finished products for subsequent hot rolling in the finishing mills. The cooling is achieved through spray cooling, and the rate and uniformity of this heat removal are critical to the microstructure and quality of the final product. Molten steel, or other metal, is poured from a ladle into a copper mold, which is cooled by circulating water, known as primary cooling. The peripherally solidified strand is then extracted from the bottom of the mold and is entering the secondary cooling zone, in which the strand surface is sprayed with water to promote further solidification. Although the shape of the cast product is defined by the mold opening, the shape integrity and product quality are basically determined in the secondary cooling zone. For this reason, there is a great need to understand the spray and heat transfer characteristics for the spray cooling process.
The major function for the secondary cooling is to speed-up the strand solidification to produce steel with required microstructures but without generating undesirable defects [7] - [13] . Inappropriate cooling could create improper or non-uniform solidification, which can induce many types of defects, such as shape and dimension irregularities, and surface and internal cracking. For instance, surface cracks, including transverse and corner cracks, can be prevented by optimizing the spray cooling in the secondary cooling zone to limit the thermomechanical strains induced in the strand during solidification [8] [10] . Crack-free surfaces are especially critical, if direct or hot-charging rolling of the cast-strand is to be subsequently performed. Also, with appropriate secondary cooling, productivity or profitability can be enhanced by increasing the casting speed or by processing value-added special steel grades. Additional benefits by improving the secondary cooling include reduced maintenance costs and water consumption as well as extended equipment life. Indeed, secondary cooling and precise control of the heat transfer is arguably the most important element in increasing product quality and process productivity in continuous casting.
A good amount of literature exists for impingement cooling at relatively low Reynolds numbers, for applications in gas-turbine cooling or for fundamental understanding of the two-phase heat transfer [1] [3] [14] [15] . A simple, practical correlation method for large-scale cooling processes is to write the average HTC, 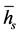 , as a function of the water volumetric flow rate, Qw [16] [17] .
, as a function of the water volumetric flow rate, Qw [16] [17] .
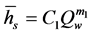 (1)
(1)
C1 is a constant that is used for different type of spray nozzle, while m1 is used to take into account the spray cooling patterns (spray overlap, injector spacing, etc.). By matching the experimental measurements of the surface temperatures with those predicted by numerical simulation, de Toledo et al. [16] obtained m1 =1.23 and C1 varies from 0.836 to 0.951, with 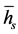 in [W/m2∙K] and Qw in [liter/min]. By fitting the modeling predictions with the temperature measurements, Jacobi et al. [7] and Muller and Jeschar [18] found that m1 was smaller, 1.15 to 1.19. In a more recent investigation, Santos et al. [17] observed that m1 was even smaller and reported that m1 and C1 were 0.556 and 366, respectively, with Qw in [L/s]. The form of this kind of correlation is set up for convenient practical applications, but due to the large number of possible spray configurations and injector types, the applicability is limited to a particular set of spray systems and also can be confusing for general use.
in [W/m2∙K] and Qw in [liter/min]. By fitting the modeling predictions with the temperature measurements, Jacobi et al. [7] and Muller and Jeschar [18] found that m1 was smaller, 1.15 to 1.19. In a more recent investigation, Santos et al. [17] observed that m1 was even smaller and reported that m1 and C1 were 0.556 and 366, respectively, with Qw in [L/s]. The form of this kind of correlation is set up for convenient practical applications, but due to the large number of possible spray configurations and injector types, the applicability is limited to a particular set of spray systems and also can be confusing for general use.
Although the twin-fluid (air/water sprays) cooling have been used for many industrial processes such as continuous casting for more than three decades, many investigators still use the correlations original developed for the single-fluid cooling. For example, Zhang et al. [19] adopted Equation (1) for their modeling of twin-fluid spray cooling with the multiplicative factor, C1, modified to C1 = 6 for liquid water spraying and C1 = 5 for air-mist spraying. In order to include air flow effects more directly, sophisticated HTC models have been developed for twin-fluid nozzle cooling. Based on the measurement by embedded thermocouples, Jacobi et al. [7] studied the heat transfer behavior during secondary cooling using twin-fluid flat-fan nozzles and found that the cooling rate (qh) is highly dependent on the surface temperature (Ts) for various mixing ratio of water and air flows. They observed that the maximum or critical heat flux took place at Ts = 200˚C, at which the complete (or maximum) wetting occurred. By re-examining the heat rate data presented by Jacobi et al. [7] , it has been found that the maximum HTC can be written as a linear function of the water volume flux (Qw).
 (2)
(2)
where D1 = 14.6, with hs,max and Qw in [kW/m2∙k] and [L/m2∙s], respectively. Indeed, the data showed that not only the HTC increased linearly with the water flow rate but also that it is independent on the air flow rate (Qa), justifying the use of Equation (1). A correlation by Ueta et al. (1990) is of interest due to its explicit dependence on the surface temperature (applicable from Ts = 600˚C ~ 1000˚C).
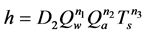 (3)
(3)
where Qa is the airflow rate, and D2, n1, n2 and n3 are correlation constants. Notably, the exponent n3 for the surface temperature is −0.136, meaning that the heat rate decreases with increasing surface temperature.
Most of the existing correlations, as noted above, include parameters such as the volumetric flow rates and surface temperature; however, they are cast in practical terms, i.e. heat transfer coefficient as a function of volumetric flow rates and empirical constants. In particular, the empirical constants vary over a wide range and are quite different for various spray configurations. The purpose of this work is to use an extensive experimental data set for heat transfer coefficients during spray cooling, and put the data in a standard form so that a universal application of the results is possible. We use the extensive data set obtained by Raudensky and co-workers [5] [6] , and seek a correlation of the form Nu = Nu(Re), where Nu is the Nusselt number and the Reynolds number. Since water is extensively used in industrial applications, the Prandtl number would be restricted to that of water. In addition, since the surface temperature has significant influence on the heat transfer we also seek to understand and parameterize the temperature effects into the correlation.
2. Experimental Details
The experiments involved using an array of injectors to spray water onto horizontal flat plates. The experimental details are fully described in Raudensky et al. [5] [6] , and here we provide a brief description in order to put the data in the context. A stainless steel plate of 30 cm × 30 cm is used (Figure 2(a)), with two rows of thermocouples embedded on backside (opposite of the cooled surface). The plate is then placed into a radiant heating device to bring the plate to about 1250˚C. The plate is removed from the radiant heater after being uniformly heated and placed over the moving injector array, which was placed 190 mm above the plate. Multiple passes of the injector arrays are made over the heated plate, and the temperatures are measured using the thermocouple array until the plate cools down to a temperature of approximately 100˚C. The temperature data as a function of time can be used to calculate the heat transfer coefficient, knowing the mass and specific heat of the metal plate.
Lechler 660.604, 660.674, and 660.804 nozzles [20] were used in the injector array, which sprayed water from top to bottom toward the heated plate as shown in Figure 2(a). These nozzles produce full elliptical spray patterns, with nearly uniform flow distributions, with different nozzle numbers having increasing bores so that a range of water volumetric flow rates from 2.22 to 15.81 liters/min per nozzle can be generated as function of the injection pressure. The elliptical impaction zones (the eight vertical rows of ellipses in Figure 2(b)) were angled alternately at + and −30 degrees as shown in Figure 2, and different spacing between the injectors allowed for different coverage and more importantly different total volumetric flow rates onto the surface. Here, the spray impaction pattern corresponds to the water reaching the surface from the injector. In Figure 2, 8 rows of injectors are used in the lateral (left-right) direction, with 7 injectors per row (top to bottom). The number of rows of injectors was fixed at 8, but the spacing and therefore the number of injectors per row was varied. The total mass flow rate and Reynolds number, then, is a function of the spray flow that impinges on the plate due to a single row (this can easily be figured out geometrically using the divergence angle of the spray and the stand-off distance), as the plate is traversed in the lateral direction (left-right in Figure 2(b)). The divergence angle was 110˚, the stand-off distance 24 cm, and the lateral speed, 1 m/s. The volumetric flow rate of different injectors is shown in Table 1. Therefore, the impact velocity is calculated by the (number of injectors) × (volumetric flow rate per injector)/(total spray impact area). The total spray impact area is πab (the elliptical pattern area) × (number of injectors). The stand-off distance was fixed, but the number of nozzles ranged from 20 to 60, which led to a large range of Reynolds numbers (55,000 to 580,000). As shown in Table 1, the injector type and flow rates were varied by changing the injection pressure. Based on the manufacturer’s data [20] , the injection velocities are estimated to range from 3.0 to 5.2 m/s for Lechler 660.604 nozzle, 4.2 to 7.8 m/s for 660.674, and 7.4 to 16.4 m/s for 660.804 nozzle.
![]() (a)
(a)![]() (b)
(b)
Figure 2. A schematic/photograph of the experimental setup (a) and spray impaction pattern on the surface (b).
![]()
Table 1. Flow rates for the nozzles, at different injection pressures.
3. Results and Discussion
The control parameters for industrial applications of spray cooling are injector type/bore diameter, injection pressure, injector lateral and longitudinal spacing. The optimum configuration should lead to uniform and sufficiently rapid cooling of the hot surface. The possible permutations of the above parameters can be overwhelming large, and one needs a universal correlation for the heat transfer rate based on the transport physics during spray cooling. It is evident that heat transfer during spray cooling depends primarily on the Reynolds number, or the volume of the flow in contact with the surface. Thus, many of the injector configuration parameters can be “compressed” into the Reynolds number of the flow. First, the injector lateral spacing only concentrates more or less of the fluid onto the surface, as does the injection pressure which increases the volumetric flow rate. We look at the geometry of the sprays as in Figure 2, and can deduce the percentage of the spray from the outside injectors that falls on the surface while assuming uniform flow speed across the spray. Due to the acute angle of the spray pattern, the outside injectors in Figure 2 have small percentage of flow falling onto the surface, while the inner four injectors carry majority of its flow onto the surface. The injection pressure is more straightforward in that the volumetric flow rate is determined as a function of the injection pressure from the injector manufacturer’s specifications. Thus, many of the injection parameters can simply translated into the volumetric flow rate onto the surface, and therefore the Reynolds number based on the total water flow rate. The relevant length scale used in the Reynolds number is the dimension of the surface, while the water density and viscosity are also used. Since the average heat transfer coefficient is calculated based on multiple thermocouple measurements, we can also convert the heat transfer coefficient to the average Nusselt number, again using the length of the plate and the water thermal conductivity.
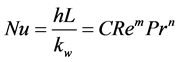 (4)
(4)
Based on this logic, we can find a generalized Nu-Re correlation, using the data set in which many of the injection parameters were varied. The length scale, L, in the Reynolds number is the lateral dimension of the substrate. The results are plotted in Figure 3, where all of the data are included as individual data points and a least-square fit curve is found from this data set. The departure from the curve to each data point thus represents the potential data uncertainty. The scatter in the data tends to increase with increasing Reynolds number, but a least-square fit curve through the line yields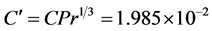 , m = 0.727 in Equation (4) and Figure 3. Equation (4) and Figure 3 show that for any water injection configuration at these Reynolds numbers (Re > 100,000) the average Nusselt number is a function only of the Reynolds number and water temperature (see below), and that only the Reynolds number needs to be evaluated based on the volumetric flow rate, which is easily obtained. The Nu-Re relationship can also be used to find the local averaged heat transfer rate, by assessing the local flow rate and therefore the local Reynolds number in divergent sprays.
, m = 0.727 in Equation (4) and Figure 3. Equation (4) and Figure 3 show that for any water injection configuration at these Reynolds numbers (Re > 100,000) the average Nusselt number is a function only of the Reynolds number and water temperature (see below), and that only the Reynolds number needs to be evaluated based on the volumetric flow rate, which is easily obtained. The Nu-Re relationship can also be used to find the local averaged heat transfer rate, by assessing the local flow rate and therefore the local Reynolds number in divergent sprays.
It is also interesting that the Nusselt number correlation shown in Figure 3 is similar to that for turbulent convection heat transfer for a parallel flow over a flat plate, where the coefficients are C = 3.7 × 10−2 and m = 0.8, but of course with a factor of Pr1/3 multiplying the Reynolds number dependence (Nu = CRemPr1/3). If we
![]()
Figure 3. Nusselt number plotted as a function of the Reynolds number, for various injector sizes, injection pressures, number of injectors and upward/downward injection. The range of test conditions is discussed in the Experimental Details section above. The solid line is Nu = 3.7 × 10−2 Re0.8, found from least-square fit through all of the data.
take the Prandtl number of the water to be 3.42, then the coefficient for the correlation shown in Figure 3 (or Equation (4)) is modified to, C/Pr1/3 = 1.9849 × 10−2, which is smaller than that for heat transfer over a flat plate, but still of similar order of magnitude. The explanation is that even though the spray is perpendicular to the plate in the current data set, the underlying heat transfer mechanism is the cooling by the liquid flow spreading over the hot surface at high Reynolds numbers. Due to the geometry of the flow, where a number of jet flows spread over the plate, the heat transfer is apparently less effective, resulting in a smaller Nusselt number as a function of the Reynolds number.
During spray cooling, complex flow structure develops near the hot surface due to the heat flux can easily cause phase change, creating vapor film near the surface. The vapor has much lower thermal conductivity than liquid, and therefore formation of vapor bubbles or films leads to a significant reduction in the heat transfer coefficient, called the Leidenfrost effect. In the current experimental data set, this complex transition can be observed as the temperature is continuously measured during multiple passes of the injector array. The data presented in Figure 3 have been taken at the surface temperature of 1000˚C, beyond the Leidenfrost point, so that they are representative of heat transfer during film boiling regime. This is the more critical heat transfer during practical applications. Subsequent heat transfer at lower surface temperatures will undergo a dramatic increase at the other side of the Leidenfrost point, and the data in the lower temperature regimes are currently also being analyzed. The effect of water temperature is quite pronounced in this heat transfer regime. In single-phase heat transfer, the heat rate is determined by the Newton’s cooling law, where the temperature difference (between the surface and water) dictates the total heat rate. However, the heat transfer coefficient stays constant. As noted above, at sufficiently high surface temperatures during spray cooling, the water can undergo nucleate or film boiling, leading to bubble/liquid flows over the surface. For temperature ranges of interest during metal production, the surface temperature is so high that typically film boiling occurs, and this has a large influence on the heat transfer. For spray cooling involving water, water temperature increase of 5˚C to 10˚C can bring the water closer to the onset of film boiling so that water temperature becomes an important parameter. In a separate set of experiments, the water temperature was varied from 20˚C, 40˚C to 60˚C at three different Reynolds numbers, and the resulting Nusselt number is plotted as shown in Figure 4. The Reynolds numbers are varied, as discussed in the Experimental Details section, while the water temperature was controlled with a pre-heater.
The effect of water temperature can also be incorporated through the Nusselt number.
 (5)
(5)
![]()
Figure 4. Heat transfer coefficient plotted as a function the water temperature at various Reynolds numbers. The Reynolds number was varied, as discussed in the Experimental Details section. The data symbols (circle, Re = 321,000; diamond, Re = 244,000; +, Re = 210,000) represent experimental data, and the lines theoretical result.
We consider the physics of the heat transfer to be the same in two-phase flow over the surface, and the primary mechanism of the change in the heat transfer coefficient is due to the reduced thermal conductivity of the vapor phase. The definition of the Nusselt number, as in Equation (5), shows that if the thermal conductivity is decreased, then the heat transfer coefficient will be reduced.
 (6)
(6)
Thus, in order to determine the heat transfer rate during two-phase flows, we need to have an estimate of the quality in relation to the water temperature. The physics of film boiling involves water mass flux over a hot surface, where the heat transferred to the water overcomes the heat of vaporization to convert liquid into water vapor. The exact details of this two-phase flow is quite complex. However, since we are interested in the net average heat transfer effect, we can use an energy balance model to find the functional relationship between the water and surface temperatures and the quality.
If we consider the energy balance for flow over a hot surface, undergoing vaporization, we can write the following equation.
![]() (7)
(7)
Here, Δm is the vaporization rate, and hfg the heat of vaporization. We can see that the enthalpy difference and the convection heat transfer constitute the excess heat available for vaporization. We can also solve for the excess heat.
![]() (8)
(8)
Thus, the quality x depends on the excess heat represented on the RHS of Equation (8). The exact dependence is the steady-state solution to the energy equation. However, we can deduce its dependence since x = 0 when there is zero excess heat, and x à 1 if the excess heat is very large. This leads to the following form for the x dependence on the excess heat.
![]() (9)
(9)
If Tf or Ts is very large, then the exponential term tends to zero in Equation (9) and x à 1. Conversely, if Ts is less than Tsat then the argument in the exponential term can become a large negative number, and x à 0. Since the precise effects of the mass flow rate on the two temperature difference terms are not known, these two factors are the correlation constants to be used with the experimental data.
![]() (10)
(10)
We can examine the effects of water temperature, Tf, on the heat transfer coefficient using Equations ((5), (6) and (10)). We consider the physics of heat transfer to be dependent only on the Reynolds and Prandtl number, as in Equation (4). This gives the heat transfer coefficient change as a function of the effective thermal conductivity, which changes with the fluid temperature according to Equations ((6) and (10)). The comparison is shown in Figure 4 where the effect of the fluid temperature is captured reasonably well, with correct inflections. The constants A1 and A2 have been found through comparison with experimental data and are listed in Table 2.
![]()
Table 2. Empirical constants A1, and A2 used in assessing the temperature effects on the Nusselt number in Equation (10) and Figure 4.
Experimental data also show that the surface temperature has an effect on the heat transfer coefficient. This is also apparent in Equation (9), where the higher surface temperature provides more excess heat for vaporization of the fluid layer close to the surface. The heat transfer model is able to predict the surface temperature effect reasonably well at low water temperatures of 20˚C and 40˚C. However, at 60˚C the predicted curve is qualitatively different from data, an inflection occurs at surface temperature of about 500˚C. Thus, there may be some additional physics that need to be considered at high fluid temperature, which are currently being investigated in this laboratory. For example, the constants A1 and A2 in Table 1 follow the expected trend where A1 increases with the Reynolds number. However, the magnitude is small in comparison to the product of the mass flow rate and the specific heat in Equation (9). Thus, perhaps this term should be computed relative to the heat of vaporization. The constant A2, on the other hand, increases with the Reynolds number, reflecting the fact that the Reynolds number enhances the heat transfer coefficient.
4. Conclusion
A large set of experimental data on spray cooling of hot surfaces with water has been analyzed, including the water temperature effects. For large-scale cooling, such as in industrial processes, large number of injection parameters such as number, type, pressure, and angle of the spray injection has led to a multitude of correlations that is included at times some of these injection parameters. However, by synthesizing a set of experimental data where all of the above parameters have been varied, we find that the Nusselt number and therefore the heat transfer coefficient can be cast as a function only of the Reynolds number. Also, the temperature effects can be accounted for by making use of the energy balance.
Acknowledgements
This experimental part of the current work was financially supported by the MEYS, under program NPU I, Project LO1202.
Nomenclature
A = surface area
A1, A2 = constants in Equation (10)
C = a constant in Equation (4)
C1 = a constant in Equation (1)
cp = specific heat
D1 = a constant in Equation (2)
D2 = a constant in Equation (3)
h = heat transfer coefficient
hfg = heat of vaporization
hs,max = maximum heat transfer coefficient
![]() = average heat transfer coefficient (HTC)
= average heat transfer coefficient (HTC)
k = thermal conductivity
keff = effective thermal conductivity of the thermal boundary layer
kf = thermal conductivity of the liquid phase
kg = thermal conductivity of the vapor phase
L = length scalem = constants in Equation (1) and Equation (4).
m= exponent for the Reynolds number in Equation (4).
m1 = a constant in Equation (1)
n1, n2, n3 = correlation constants in Equation (3)
Nu = Nusselt number = hL/k
Pr = Prandtl number
Qa = air flow rate
Qw = water flow rate
qexcess = “excess” heat rate in Equation (8)
Re = Reynolds number
Tf = water temperature
Ts = surface temperature
Tsat = saturation temperature
x = quality
μ = viscosity
ρ = density
NOTES
![]()
*Corresponding author.