Criticality Analysis on Value-at-Risk Model of Loan-to-Value Ratios Decision in Inventory Financing of Supply Chain Finance ()
Received 25 November 2015; accepted 10 December 2015; published 15 December 2015
Subject Areas: Operations Management, Supply Chain Management
1. Introduction
In recent years, supply chain finance (SCF) has been increasingly looked at by European and global enterprises and financial institutes. A survey of “How has the importance of supply chain finance to your organization changed over the past 12 months?” from the Treasury Today’s European Corporate Treasury Benchmarking Study 2010 in association with J.P. Morgan shows that 42.2% of the respondents have a view of “Increased in importance”; proportions of “Remained the same” and “Not on our agenda” are respectively 31.6% and 25.3%; only 0.9% of respondents think that “decreased in importance”. In fact, the modern concept of SCF stems from the world-class enterprises’ global business outsourcing under the trend of cost minimization in 1980s [1] and is typically defined as a combination of services and technology solutions that links buyers, suppliers and finance providers to improve the visibility of financing cost, availability and delivery of cash when supply chain events take place [2] .
Comparing with the traditional credits mainly providing letter of credit business, the SCF concentrates on providing account prepayments financing, inventory pledged financing and factoring [1] , which is increasingly looked at by European and global enterprises reforming of the business model of traditional finance. Because it has advantages of improving the credit availability, supporting the large enterprises to develop credit terms with their suppliers who can also use their credits with the credit qualities of receivable debtors to finance their receivables with a favorable rate, enhancing the margins and consumer relationships of borrowers and offering openness financing to small and medium enterprises [3] . In summary, SCF benefits both lenders and borrowers with more chances and higher profits, however, SCF is currently a relative young discipline, which has numerous problems, whether have been existed in traditional inventory financing or newly generated with the development of SCF.
The objective of this paper is to show the nonlinear relationship between loan-to-value ratio (LTV) and loan value-at-risk (VaR) in inventory financing of SCF. Commercial banks, suppliers (such as manufacturers), buyers (such as retailers) and logistic enterprises participate in this financial behavior. Relying on suppliers’ credits on which their cooperating with the banks based, buyers generally have budget constraints or financing with strategies, finance their debtors to commercial banks with the purchase pledging and regulating by the enterprises closely cooperating with banks who offer financial supports for buyers to place orders being used to pay off the loans after selling in a commodity market. In this financing business, banks play a key role in mitigating the capital pressures in supply chain, however, undertaking a level of risks, which may be mainly caused by the marketability and market price of pledged inventory with the character of self-liquidation [4] . For this point of view, Hu and Huang (2009) also indicate that a higher proportion of intermediate goods act as collateral with weaker marketability and stable distribution of market price comparing to materials and finished products may cause higher risk to banks in inventory financing of SCF [1] . Thus, Buzacott and Zhang (2004) analyze reasonably that an asset-based loan limit should be set for each loan by linking that to the borrower’s assets and liabilities in case of over-order by buyers [5] and Yi and Zhou (2011) consider the buyback-guarantee of suppliers when there exists surplus inventory pledged without selling in the commodity market [6] .
Given the self-liquidity feature of inventory financing in SCF, we mainly analyzed the banks’ loan-to-value ratio (LTV) decision, which is effective in controlling banking stability through decreasing the sensitivity of mortgage default risk to fluctuation of assets price [7] - [9] . For this reason, LTV defined as the ratio of a loan to an asset’s appraised value or purchase price (Wiki) have been widely looked at by financial institutions or departments and academic researchers, for instance, maximum LTV on mortgages have been adopted as a micro- prudential instrument by some European countries to fulfill the policy gaps. Similarly, the max LTV of 70% has been applied as a long-term regulatory policy by Hong Kong Monetary Authority (HKMA) in 1995 [7] . From the perspective of lender and borrower, Buzacott and Zhang (2004) analyze the linear relationship between LTV and maximum order quantity, which affects the retailer’s bankruptcy risk and bank’s return [5] . Li and Feng (2007) analyze the LTV decision of downside-risk-constraint banks when the prices of their inventory pledged follow the general distribution and several kinds of special specific ones, which indicate that the analytics of loan-to-value ratios can be solved under static pledge fashion only if the price distributions of the inventory are required at the end of the loan [10] . Additionally, Qin and Yang (2009) empirically illustrate the positive correlation relationship between LTV and loss given default, in their opinion, updated LTV can enhance loan risk segmentation although additional costs may be added [11] . Similarly, Liberti and Mian (2010) indicate that there is a mutual influence between the LTV and strategic default, that is, the more collateral required, the less possibility for borrowers to default strategically [12] . However, few researches concentrate on the relationship between LTV and loan VaR in inventory financing of SCF.
In uncertainty environment, risks and losses are inevitable, but the worst consequence may be predicted, and the measures according to extreme situations are also useful to common, that is, the extreme case may be better to reflect the real world. Just like VaR, the research method used in this paper, which can summarize the worst dollar loss over a target horizon that will not exceed with a given level of confidence and be applied to most financial prices, stock prices, bond prices, exchange rates and commodities. For instance, the Basel Committee on Banking Supervision declared that the banks market risks could be measured by the combination of VaR and internal model. Furthermore, as a standard method for measuring and reporting market risk, VaR not only reforms the traditional financial risk management but also can easily be used to measure and report market risks in a single number with unified unit and to communicate with the top management, shareholders as well as help financial institutions to confront their exposure to financial risks [13] [14] . For this reason, Duffie and Pan (1997) give an overview of the VaR methods from a perspective of price risk [15] . He Juan (2012) predicts the VaR of steel during various loan periods and gets the impawn rate, which may both control risk and decrease efficiency loss comparing with the experience method that the impawn rate is generally lower than 70%, by setting a model with the formula AR(1)-GARCH(1,1)-GED. A parameter K is introduced, which can improve its risk coverage [16] . In their views, the pledged inventories having autocorrelation are different from financial assets because of fat-tails and so on, meaning the market risk of the collateral may derive from some extreme situations such as dramatic price-decline. Different from traditional VaR method, however, the financial and procurement positions of the borrower were incorporated into VaR model in this paper, that is, the critical value of LTV corresponds to extreme values of loan VaR based on the parameters relating to the borrower’s financial and purchase conditions as well as the loan itself in inventory financing of SCF at extreme situations.
By considering the first order and second order conditions of loan VaR model with the general distribution and log-normal distribution of the buyer’s demand under extreme situations of dramatic price-decline, the analytic formulas of the critical order quantity and critical LTV were calculated. The former determines the monotonic property of the linear relationship between LTV and loan VaR when the order quantity is not limited; while the later has an influence on the LTV corresponding to extreme values of loan VaR, and the recessive analytic formula is provided from which the critical values of LTV corresponding to the local maximums and minimums of loan VaR can be calculated, which prevent the bank from the extreme potential loss deriving from LTV decisions. Furthermore, the impacts of parameters relating to borrower’s financial position, procurement and the loan itself on the relationship between LTV and loan VaR were analyzed in numerical examples. However, the problems of setting loan margin, setting the proportion of inventory pledged to total purchase amount, choosing semi-finished product as inventory pledged and LTV decisions of the bank with an attitude of risk- neutral in inventory financing of SCF were not analyzed in this paper.
This paper is organized as follows. Section 2 made several basic assumptions being followed by establishing the model. Section 3 analyzed the model from the perspectives of linear and nonlinear relationships of LTV and loan VaR. In Section 4, numerical examples were used to explore the linear and nonlinear relationships between LTV and loan VaR with considering the affection parameters. The conclusion was made in Section 6.
2. Model Assumption and Model Set-Up
Inventory financing of SCF is different from the traditional financing with the following properties: 1) The third party, frequently the core enterprise in supply chain, secures for the borrower, such as the retailer in supply chain, with the credit itself instead of her property; 2) Self-liquidity exists in the financing with pledging the borrower’s purchase, which is used to repay the loan through the commodity market; 3) Borrowers without real properties may finance from the bank in a shorter loan period. Thus, basic assumptions are needed before modeling.
2.1. Model Assumption
The nonlinear relationship between LTV and loan VaR of the commercial bank in supply chain inventory financing is analyzed. It refers to banking decisions that contain loan interest rate, loan period and LTV; the borrower’s initial wealth, purchase or demand that will act as the collateral, which can be sold in the commodity market for paying off the loan. Thus, we set up model based on the following assumptions.
1) Loan interest rate remains stable during the loan period within one year. The sales cycle of pledged inventory (liquidity) will be considered when the bank makes decisions of loan periods, which are negatively related to the liquidity of the collateral, and loan Interest rates are normally expressed for a period of one year.
2) Initial wealth is the only factor classifying retailers by the bank and not only retailers being lack of cash but also the ones owning enough initial wealth may participate in supply chain inventory financing.
3) The retailer orders from her suppliers without idea of actual demand, only the probability distribution of demand [5] .
2.2. Model Set-Up
We assume that the retailer owning initial wealth h orders the size q at a wholesale price p from her suppliers with no idea of the actual demand, only the probability distribution of demand  given by
given by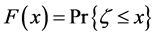 . Let
. Let ,
, 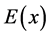 represents the expectation of
represents the expectation of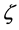 . The retailer is required to surrender a loan margin m, let
. The retailer is required to surrender a loan margin m, let ,
, 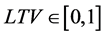 and
and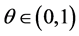 .
.
2.2.1. Loan Amount
The loan that is represented as l can be differ from the retailer’s initial wealth h when (1) h is little even cannot afford the m ( , i.e.,
, i.e., )and m will be deducted from loan amount calculating by
)and m will be deducted from loan amount calculating by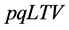 ; (2) h is enough for m while still cannot afford the purchase amount (
; (2) h is enough for m while still cannot afford the purchase amount (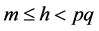 , i.e.,
, i.e.,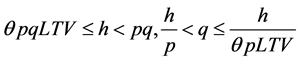 ); (3) h is enough for the purchase amount (
); (3) h is enough for the purchase amount (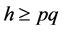 , i.e.,
, i.e.,![]() ), the probability of choosing a loan is
), the probability of choosing a loan is ![]() and
and ![]() otherwise. In summary, Loan amounts l actually supplying by the bank differ according to the retailer’s initial wealth h, and l is given by
otherwise. In summary, Loan amounts l actually supplying by the bank differ according to the retailer’s initial wealth h, and l is given by
![]() (1)
(1)
where ![]() represents loan-to-value ratio,
represents loan-to-value ratio, ![]() represents the proportion of the margin to a loan amount, p represents wholesale price, q represents the retailer’s order quantity and Q represents the probability of borrowing when a retailer has enough h for affording the purchase.
represents the proportion of the margin to a loan amount, p represents wholesale price, q represents the retailer’s order quantity and Q represents the probability of borrowing when a retailer has enough h for affording the purchase.
2.2.2. Expected Return to Bank
Follows the Equation (1), the return of the bank ![]() and expected return of the bank
and expected return of the bank ![]() can be given by Equation (2) and Equation (3), where R represents the loan interest rate,
can be given by Equation (2) and Equation (3), where R represents the loan interest rate, ![]() and T represents the loan period within one year.
and T represents the loan period within one year.
![]() (2)
(2)
![]() (3)
(3)
2.2.3. Market Risk
The bank who participates in supply chain inventory financing is risk averse and requires finished products or raw materials as collaterals. Banks prefer finished goods or raw materials to semi-finished products with a high specificity and a low liquidity in the commodity market.
One of the significant characters of supply chain inventory financing is self-liquidating, which the payment of a loan derives from sales of a trade financially supporting by the bank. In this paper, a retailer purchases products depending on a financial support of a bank who requires the borrower pledging the whole or part of the products as collaterals, which can be paid off after being sold in the market, that is, market price and interest rate may become factors of leading to market risk. In model assumption, we assume the interest rate remains stable during the loan period and the market price of the pledged inventory is the only factor affecting the market risk, that is, the bank’s lowest return ![]() follows the lowest unit market price of the collateral
follows the lowest unit market price of the collateral![]() , which will not be exceed with a confidence level
, which will not be exceed with a confidence level ![]() (e.g. 95%).
(e.g. 95%).
2.2.4. VaR Model
VaR can be defined as the dollar loss relative to what was expected for an asset over a target horizon that will not be exceed with a given level of confidence, which implies the identity of the asset during a given horizon, However, both return and loss of a loan in supply chain inventory financing derive from the market value of the pledged inventory. This means there exist a contradiction when we analysis the market risk of bank using the VaR method. For dealing with this problem, we define ![]() as follows
as follows
![]()
where only consider the lowest market value of the “discounted” (corresponding to LTV) collateral but not all. Thus, according to the definition of VaR, the loan LTV of the bank in supply chain inventory financing over a target horizon T at a confidence level of![]() ,
, ![]() , can be given by
, can be given by
![]()
Followed by first-order and second-order conditions, which were given by
![]()
![]()
where ![]() represents the expectation of the retailer’s demand
represents the expectation of the retailer’s demand![]() , which follows a general probability distribution,
, which follows a general probability distribution,![]() ,
, ![]() and
and![]() .
.
3. Model Analysis
In model assumption, we assumed that suppliers only know the probability distribution of the retailer’s demand ![]() but not the actual amount, follows it, several simple properties were analyzed by considering the first-order and second-order conditions of
but not the actual amount, follows it, several simple properties were analyzed by considering the first-order and second-order conditions of![]() , which relative to the critical order quantity
, which relative to the critical order quantity ![]() and the critical loan-to- value ratios
and the critical loan-to- value ratios![]() . We firstly assume the retailer’s demand
. We firstly assume the retailer’s demand ![]() follows general probability distribution, followed by linear and nonlinear analysis of the relationship between LTV and loan VaR, which is also analyzed based on the assumption of log-normal distribution of
follows general probability distribution, followed by linear and nonlinear analysis of the relationship between LTV and loan VaR, which is also analyzed based on the assumption of log-normal distribution of![]() .
.
3.1. Monotonic Impact of Critical Order Quantity q* in Linear Analysis
Either borrowers or lenders, the order quantity q can be one of the key factors in inventory financing. Although merely being able to directly affect by commercial banks who may prudentially consider the order quantity to make banking decisions and prevent themselves from the risk of over-order. For this reason, Buzacott and Zhang (2004) analyze the maximum order quantity, which can affect the retailer’s bankruptcy risk and bank’s return. In their model, the maximum order quantity is determined by the retailer’s initial wealth, unit purchase cost and a proportion similar to LTV. In this paper, the linear relationship between LTV and loan VaR is analyzed, followed by the condition of the linear relationship, and critical order quantity![]() , which monotonically influences the linear relationship, negative with
, which monotonically influences the linear relationship, negative with ![]() and positive with the expectation of retailer’s demand,
and positive with the expectation of retailer’s demand,![]() .
.
Lemma 1. There is linear relationships between LTV and loan VaR following ![]() or the equation that is given by
or the equation that is given by
![]()
where ![]() is the probability cumulative distribution function of general distribution of the retailer’s demand
is the probability cumulative distribution function of general distribution of the retailer’s demand![]() , c is a constant and
, c is a constant and ![]() and
and ![]() is the proportion of the retailer’s initial wealth to her purchase costs.
is the proportion of the retailer’s initial wealth to her purchase costs.
Specifically, ![]() is a monotonically increasing function of LTV if
is a monotonically increasing function of LTV if ![]() and otherwise if
and otherwise if![]() , where
, where ![]() can be given by
can be given by
![]()
and ![]() represents the proportion of unit purchase cost to the lowest unit market price of the collateral.
represents the proportion of unit purchase cost to the lowest unit market price of the collateral.
Proof. Obviously, ![]() if
if![]() , where there exists a linear relationship between
, where there exists a linear relationship between ![]() and
and![]() .
.
If![]() , since
, since![]() , hence the positive of negative of the second order condition depends on that of
, hence the positive of negative of the second order condition depends on that of![]() , which is given by
, which is given by
![]()
Let ![]()
![]()
Also consider the first order condition, let
![]()
![]()
![]()
Then ![]() (c is a constant).
(c is a constant).
![]() ,
, ![]() , Q.E.D.
, Q.E.D.
![]() and
and ![]() are main influenced factors to
are main influenced factors to ![]() from the perspective of risk attitudes of the bank, since it’s generally difficult for the bank in controlling R, T,
from the perspective of risk attitudes of the bank, since it’s generally difficult for the bank in controlling R, T, ![]() and p. In this paper,
and p. In this paper, ![]() is mainly analyzed and
is mainly analyzed and ![]() is viewed as a criterion to different borrowers. It can clearly be seen that the expected lowest market price or the extreme market price-decline of the collateral can reflect one’s risk-reverse level, the lower
is viewed as a criterion to different borrowers. It can clearly be seen that the expected lowest market price or the extreme market price-decline of the collateral can reflect one’s risk-reverse level, the lower![]() , the higher level of risk averse, furthermore, the higher critical order quantity
, the higher level of risk averse, furthermore, the higher critical order quantity![]() . Although the loan VaR decreases when
. Although the loan VaR decreases when![]() , as a matter of fact, the one with a risk-averse attitude cannot accept the retailer’s order quantity higher than
, as a matter of fact, the one with a risk-averse attitude cannot accept the retailer’s order quantity higher than![]() , and prefer that
, and prefer that![]() , which may lead the loan VaR increasing companion with the order quantity of the retailer.
, which may lead the loan VaR increasing companion with the order quantity of the retailer.
3.2. Critical LTV to Extrema of Loanvar
In the above analysis, it’s mainly to analyze the monotonically affection of the critical order quantity ![]() in the linear relationship between LTV and loan VaR, however, it’s also analyzed in nonlinear relationship between them. Furthermore, the affections of initial wealth, the expected lowest market price of the collateral as well as the loan period to the critical LTV and extreme values of loan VaR are also considered. Frequently, LTV can be an ex ante approach to prevent the bank from the potential loss such as the max LTV. For example, HKMA has regulated the max LTV of 70%, while Korteweg and Sorensen (2011) analyze the LTV distributions of buyers and sellers in household mortgage, followed by the values of LTV are prominent around 0.8.Similarly, Haan and Andre (2011) advices that loans with the LTV exceeding 0.8 should be required mortgage insurance. In this paper, through the nonlinear analysis between LTV and loan VaR, we discuss the critical LTV, which has an influence on the extreme values of loan payments from the perspective of VaR followed by Lemma 2 and Theorem 1.
in the linear relationship between LTV and loan VaR, however, it’s also analyzed in nonlinear relationship between them. Furthermore, the affections of initial wealth, the expected lowest market price of the collateral as well as the loan period to the critical LTV and extreme values of loan VaR are also considered. Frequently, LTV can be an ex ante approach to prevent the bank from the potential loss such as the max LTV. For example, HKMA has regulated the max LTV of 70%, while Korteweg and Sorensen (2011) analyze the LTV distributions of buyers and sellers in household mortgage, followed by the values of LTV are prominent around 0.8.Similarly, Haan and Andre (2011) advices that loans with the LTV exceeding 0.8 should be required mortgage insurance. In this paper, through the nonlinear analysis between LTV and loan VaR, we discuss the critical LTV, which has an influence on the extreme values of loan payments from the perspective of VaR followed by Lemma 2 and Theorem 1.
Lemma 2. A nonlinear relationship between LTV and loan VaR exists when![]() , followed by
, followed by ![]() existing if
existing if![]() ; and
; and ![]() existing if
existing if![]() , where
, where![]() ,
,![]() and
and ![]() respectively denotes the local maximum and local minimum of loan VaR.
respectively denotes the local maximum and local minimum of loan VaR.
Proof. Let![]() , then
, then ![]() can be given by
can be given by
![]() ,
,
Since![]() , then
, then
![]() (4)
(4)
Follows the Equation (4), then
![]()
That is, the local maximum of loan VaR exists if![]() ; the local minimum of loan VaR exists if
; the local minimum of loan VaR exists if![]() . Q.E.D.
. Q.E.D.
Lemma 2 indicates that the nonlinear relationship between LTV and loan VaR exists under certain conditions, that is, there exists corresponding values of loan LTV leading to extreme VaR of loan. ![]() and
and ![]() may not be the minimum or maximum in the interval of LTV from a to 1 where a is a positive number that is closed to zero, whereas the results of the convexity and concavity of the curve. From Lemma 2, it’s not difficult to see that lower LTV may cause higher loan VaR, whereas, higher LTV corresponds to lower loan VaR. That means, low LTV may not be safe, whereas, relative high LTV may decrease loan VaR. The critical LTV
may not be the minimum or maximum in the interval of LTV from a to 1 where a is a positive number that is closed to zero, whereas the results of the convexity and concavity of the curve. From Lemma 2, it’s not difficult to see that lower LTV may cause higher loan VaR, whereas, higher LTV corresponds to lower loan VaR. That means, low LTV may not be safe, whereas, relative high LTV may decrease loan VaR. The critical LTV ![]() can prevent them from the potential loss of loan deriving from the LTV decisions relying on experience, which may be generally useful. Specifically, the bank may make LTV lower when the acceptable LTV is lower than the critical one, otherwise, higher the value of LTV.
can prevent them from the potential loss of loan deriving from the LTV decisions relying on experience, which may be generally useful. Specifically, the bank may make LTV lower when the acceptable LTV is lower than the critical one, otherwise, higher the value of LTV.
Lemma 2 identifies the properties of convexity and concavity of LTV-loan VaR curve, which denotes the existing of the extreme value of loan VaR, then the Theorem 1 is is immediately followed by the analytic formula of ![]() or
or![]() .
.
Theorem 1. Assume the retailer’s demand ![]() follows the general probability distribution
follows the general probability distribution![]() , then
, then ![]() or
or ![]() follows the equation that is given by
follows the equation that is given by
![]()
where ![]() and
and ![]() respectively denotes the value of LTV corresponding to the local maximum and local minimum of loan VaR,
respectively denotes the value of LTV corresponding to the local maximum and local minimum of loan VaR, ![]() ,
, ![]() ,
, ![]() repre-
repre-
sents the proportion of the lending margin to loan amount, p represents unit wholesale price, h represents the retailer’s initial wealth, ![]() represents the expectation of the retailer’s demand
represents the expectation of the retailer’s demand![]() ,which follows the general probability distribution, Q represents the probability of lending a loan by a retailer when his h is enough for affording the purchase, R represents the loan interest rate and T is the loan period within one year.
,which follows the general probability distribution, Q represents the probability of lending a loan by a retailer when his h is enough for affording the purchase, R represents the loan interest rate and T is the loan period within one year.
Proof. Since there exists the maximum and minimum of loan VaR, ![]() follows from Lemma 2. Let
follows from Lemma 2. Let![]() , that is
, that is
![]()
then
![]()
then
![]()
where
![]()
Assume
![]()
then
![]()
Then
![]()
Then the differential equation is solved as follows,
![]()
Since![]() , then
, then![]() ,
,
Since ![]() , then,
, then, ![]()
Then, ![]()
Since, ![]()
Then, ![]()
Then, ![]()
![]() , Q.E.D.
, Q.E.D.
To some extent, ![]() and
and ![]() can prevent the bank from the risks of potential loss from the LTV decision, furthermore, they can improve one’s expected return and profits even in the serious case. Additionally, from the perspective of borrowers, relatively higher LTV help them receive more loan based on the certain inventory pledged or collateral, and inject more capital into the supply chain.
can prevent the bank from the risks of potential loss from the LTV decision, furthermore, they can improve one’s expected return and profits even in the serious case. Additionally, from the perspective of borrowers, relatively higher LTV help them receive more loan based on the certain inventory pledged or collateral, and inject more capital into the supply chain.
3.3. Specific Analysis Followed by Log-Normal Distribution of z
Based on the above analysis, we specifically assume the retailer’s demand ![]() follows lognormal distribution and have a research. Generally, the probability distribution is assumed to be normal if that of a variable is unknown, however, the cumulative distribution function of normal distribution is symmetric about its mean and the domain of that is over the entire real number, which is unsuitable to positive variables, such as the order quantity q in this paper. For this reason, we assume the retailer’s demand
follows lognormal distribution and have a research. Generally, the probability distribution is assumed to be normal if that of a variable is unknown, however, the cumulative distribution function of normal distribution is symmetric about its mean and the domain of that is over the entire real number, which is unsuitable to positive variables, such as the order quantity q in this paper. For this reason, we assume the retailer’s demand ![]() follows lognormal distribution with only
follows lognormal distribution with only
positive real numbers (Wiki) with parameters ![]() and
and![]() , that is,
, that is,![]() . Immediately, the Lemma 3, Lemma 4 and Theorem 2 are followed by the Lemma 1, Lemma 2 and Theorem 1.
. Immediately, the Lemma 3, Lemma 4 and Theorem 2 are followed by the Lemma 1, Lemma 2 and Theorem 1.
Lemma 3. If ![]() follows log-normal distribution
follows log-normal distribution ![]() with parameters
with parameters ![]() and
and![]() , that is,
, that is, ![]() , then there exists a linear relationship between LTV and loan VaR follows
, then there exists a linear relationship between LTV and loan VaR follows ![]() or the equation () established, which is
or the equation () established, which is
![]() (
(![]() is a constant and
is a constant and![]() ),
),
where![]() ,
, ![]() represents the cumulative distribution function of standard normal distribution and c is a constant. Specifically, the loan VaR has a monotonic increase with LTV if
represents the cumulative distribution function of standard normal distribution and c is a constant. Specifically, the loan VaR has a monotonic increase with LTV if ![]() and otherwise if
and otherwise if![]() , where
, where
![]()
The proof follows the Lemma 1, ![]() and
and ![]() when
when ![]() follows the log-nor- mal distribution.
follows the log-nor- mal distribution.
![]() and
and ![]() are positive with the critical order quantity
are positive with the critical order quantity![]() , the higher the values of
, the higher the values of ![]() and
and![]() , the higher the
, the higher the ![]() and the higher the value of
and the higher the value of![]() , and it’s obvious that the pair of parameters may have a more notable influence on the
, and it’s obvious that the pair of parameters may have a more notable influence on the ![]() than other parameters since they increase exponentially. Furthermore, the specific analytic formula of the critical LTV
than other parameters since they increase exponentially. Furthermore, the specific analytic formula of the critical LTV ![]() can be given if
can be given if ![]() follows the lognormal distribution, followed by Lemma 4.
follows the lognormal distribution, followed by Lemma 4.
Lemma 4. If![]() , then
, then ![]() exists as
exists as![]() , and
, and ![]() exists when
exists when![]() , where
, where![]() ,
, ![]() and
and![]() . Specially, there only exists
. Specially, there only exists ![]() when
when![]() .
.
Proof. Since![]() , then the probability density function
, then the probability density function ![]() can be given by
can be given by
![]()
and
![]()
Follows Lemma 2,
![]()
![]()
Substitute![]() ,
, ![]() from
from ![]()
Followed by
![]()
Substitute u from![]() , followed by
, followed by
![]()
where![]() .
.
Specifically, if![]() ,
, ![]() , then
, then![]() ,
, ![]() exists; if
exists; if![]() ,
, ![]() , then
, then![]() ,
, ![]() exists. Specially, if
exists. Specially, if![]() , then
, then![]() ,
, ![]() is always established because of
is always established because of![]() , that is, there only exists
, that is, there only exists ![]() if
if![]() . Q.E.D.
. Q.E.D.
Lemma 4 makes the manager of the bank clearly analyze the LTV decisions only if the initial wealth of the retailer h, the margin proportion of the loan![]() , the unit purchase cost p and the parameter
, the unit purchase cost p and the parameter ![]() are known, and the critical LTV
are known, and the critical LTV ![]() is relative to the unit procurement cost p but the order quantity q, which merely affect the nonlinear relationship between LTV and loan VaR. Additionally, the bank should evaluate h and the parameter
is relative to the unit procurement cost p but the order quantity q, which merely affect the nonlinear relationship between LTV and loan VaR. Additionally, the bank should evaluate h and the parameter ![]() through cooperating with the leading enterprise in the supply chain. Furthermore, the specific analytic formula is also given that follow immediately.
through cooperating with the leading enterprise in the supply chain. Furthermore, the specific analytic formula is also given that follow immediately.
Theorem 2. If![]() , then
, then ![]() and
and ![]() can be given by
can be given by
![]()
where![]() ,
, ![]() ,
,
![]() ,
,
![]() represents the proportion of the lending margin to loan amount, p represents the wholesale price of the pledged inventory, h represents the retailer’s initial wealth,
represents the proportion of the lending margin to loan amount, p represents the wholesale price of the pledged inventory, h represents the retailer’s initial wealth, ![]() represents the expectation of a retailer’s demand q, which follows log-normal distribution,
represents the expectation of a retailer’s demand q, which follows log-normal distribution, ![]() represents the cumulative distribution function of standard normal distribution, Q represents the probability of lending a loan by a retailer when his initial wealth h is enough for affording the purchase, R represents the loan interest rate and T is the loan period within one year.
represents the cumulative distribution function of standard normal distribution, Q represents the probability of lending a loan by a retailer when his initial wealth h is enough for affording the purchase, R represents the loan interest rate and T is the loan period within one year.
Proof. Since ![]() hence,
hence, ![]()
Follows Theorem 1, the value of LTV corresponding to ![]() and
and ![]() follow the equation that is given by
follow the equation that is given by
![]() ,
,
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() . Q.E.D.
. Q.E.D.
4. Numerical Example
Follows 3.3, log-normal distribution of the retailer’s demand ![]() was assumed in numerical example, that is,
was assumed in numerical example, that is, ![]() , and the impact of h, q,
, and the impact of h, q, ![]() , T and
, T and ![]() on the linear or nonlinear relationship of LTV with loan VaR was analyzed in 4.1 and 4.2. Among them, h and
on the linear or nonlinear relationship of LTV with loan VaR was analyzed in 4.1 and 4.2. Among them, h and ![]() are reflected by
are reflected by ![]() and
and![]() , which are the proportions of the retailer’s initial wealth to the total purchase costs and unit procurement cost to the expected lowest unit market price of the collateral or inventory pledged. Figure 1 shows the log-normal distribution of
, which are the proportions of the retailer’s initial wealth to the total purchase costs and unit procurement cost to the expected lowest unit market price of the collateral or inventory pledged. Figure 1 shows the log-normal distribution of ![]() respectively with the pair of parameters (3, 0.8), (3.5, 0.8) and (4, 0.8).
respectively with the pair of parameters (3, 0.8), (3.5, 0.8) and (4, 0.8).
The mode is the point of global maximum of the probability density function (Wikipedia)
4.1. Linear Analysis
In Lemma 3, the loan VaR has a monotonic linear-increase with LTV as q was in ![]() and a monotonic linear-decrease if
and a monotonic linear-decrease if![]() . The critical order quantity
. The critical order quantity ![]() that is positive with
that is positive with ![]() both at the situations whether
both at the situations whether ![]() or
or![]() . As an example, Let
. As an example, Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Firstly, As
. Firstly, As![]() ,
, ![]() , we varied
, we varied ![]() with three situations of
with three situations of![]() ,
, ![]() and
and![]() , followed by an increase of
, followed by an increase of ![]() that is positive with
that is positive with![]() . When
. When![]() ,
, ![]() and
and![]() ,
, ![]() , this means loan VaR is monotonically positive with LTV, while
, this means loan VaR is monotonically positive with LTV, while![]() ,
, ![]() and
and![]() ,
, ![]() , which means the loan VaR is monotonically decreased with increasing of LTV. Ob-
, which means the loan VaR is monotonically decreased with increasing of LTV. Ob-
![]()
Figure 1. Density function of log-normal distribution of the retailer’s demand z.
viously, ![]() represents the level of loan VaR, specifically, the higher the abstract of
represents the level of loan VaR, specifically, the higher the abstract of![]() , the higher the risk level when
, the higher the risk level when ![]() and otherwise if
and otherwise if![]() . Secondly, at the situation of
. Secondly, at the situation of![]() ,
, ![]() , linear relationship follows from the equation () , the affection of
, linear relationship follows from the equation () , the affection of ![]() to loan VaR was analyzed, such as, let
to loan VaR was analyzed, such as, let![]() ,
, ![]() , if
, if![]() ,
, ![]() , then
, then![]() ; if
; if![]() ,
, ![]() , then
, then![]() , that is, the borrower with less initial capital and more order quantity may suffer lower risk than that in a better capital condition. In other words, the initial wealth of the retailer merely influences the loan risk level corresponding to LTV, in fact, both
, that is, the borrower with less initial capital and more order quantity may suffer lower risk than that in a better capital condition. In other words, the initial wealth of the retailer merely influences the loan risk level corresponding to LTV, in fact, both ![]() and q mainly influenced the VaR level of the loan, like shows in Table 1.
and q mainly influenced the VaR level of the loan, like shows in Table 1.
The value of loan VaR can either be positive or negative, higher value of abstract of ![]() means higher risk level in former situation and otherwise the later. The values of loan VaR are mostly negative with variable LTV, and the higher abstract value of
means higher risk level in former situation and otherwise the later. The values of loan VaR are mostly negative with variable LTV, and the higher abstract value of![]() , the lower potential loss of the loan, that is, under the precondition of linear relationship between LTV and loan VaR, the enough order quantity acting as collateral may decrease the potential loss of loan without considering the limit of over-order, as illustrated in Figure 2.
, the lower potential loss of the loan, that is, under the precondition of linear relationship between LTV and loan VaR, the enough order quantity acting as collateral may decrease the potential loss of loan without considering the limit of over-order, as illustrated in Figure 2.
4.2. Nonlinear Analysis
Based on our analysis in Lemma 2 that higher LTV may corresponding to relatively lower loan VaR, whereas, relatively lower LTV may lead to higher risk level of potential loss of bank loan. According to Lemma 4, the local maximum and local minimum of loan VaR may respectively exist on the left and right sides of the critical LTV that can be given by
![]() , where
, where![]() .
.
According to the analytic formula of LTV*, it’s not difficult to see that LTV* is positive with ![]() and q, and is negative with the proportion of loan margin
and q, and is negative with the proportion of loan margin ![]() and the local parameter
and the local parameter ![]() of lognormal distribution of the
of lognormal distribution of the
retailer’s demand![]() . Since
. Since![]() , then the analysis of that is divided into two parts: one is based on the precondition of
, then the analysis of that is divided into two parts: one is based on the precondition of![]() , and the other will be discussed when
, and the other will be discussed when![]() . Specifically, if
. Specifically, if![]() , correspondingly,
, correspondingly, ![]() ,
, ![]() or
or![]() ; if
; if![]() , followed by
, followed by![]() ,
, ![]() or
or![]() . Furthermore, the impacts of
. Furthermore, the impacts of![]() ,
, ![]() ,
, ![]() and T on the
and T on the
nonlinear relationship between LTV and loan VaR will be analyzed. Specifically, the proportion ![]() can respectively reflect the variations of h or q, and
can respectively reflect the variations of h or q, and ![]() represents the level of fluctuation of the expected lowest unit market price of the collateral when p is some constant.
represents the level of fluctuation of the expected lowest unit market price of the collateral when p is some constant.
![]()
Figure 2. The linear relationship between LTV and loan VaR.
4.2.1. Impact of h and vmin
h and ![]() can be respectively reflected by
can be respectively reflected by ![]() and
and![]() , as an example, let
, as an example, let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . Following
. Following ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , fol-
, fol-
lowed by![]() , which is companion with Lemma 4. When
, which is companion with Lemma 4. When ![]() and
and![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() remain unchangeable, however,
remain unchangeable, however, ![]() ,
, ![]() and
and![]() , that is, the loan VaR increases from cutting down of
, that is, the loan VaR increases from cutting down of![]() . If
. If ![]() and it remains unchanged, h changes from 1.5 to 3.5,
and it remains unchanged, h changes from 1.5 to 3.5, ![]() is constant, whereas
is constant, whereas ![]() changes from 0.1429 to 0.3333,
changes from 0.1429 to 0.3333, ![]() increases from 0.3556 to 0.8298 as well as
increases from 0.3556 to 0.8298 as well as ![]() and
and ![]() respectively increase with 130.15% ((6.0632 − 2.6344)/2.6344 * 100%) and 134.31% ((8.8503 − 3.7772)/3.7772 * 100%). It can clearly be seen, loan VaR increases by the growth of h because the bank classifies the borrowers only with the initial wealth h, however, without the ability of controlling that effectively, as showing in Table 2.
respectively increase with 130.15% ((6.0632 − 2.6344)/2.6344 * 100%) and 134.31% ((8.8503 − 3.7772)/3.7772 * 100%). It can clearly be seen, loan VaR increases by the growth of h because the bank classifies the borrowers only with the initial wealth h, however, without the ability of controlling that effectively, as showing in Table 2.
From Figure 3, when![]() , loan VaR is higher than that at
, loan VaR is higher than that at![]() , whether the variation of
, whether the variation of ![]() or not, that is, the impact of
or not, that is, the impact of ![]() is more notable than h when other variables and parameters are unchanged. Furthermore, if
is more notable than h when other variables and parameters are unchanged. Furthermore, if ![]() remains constant and
remains constant and ![]() is enhanced, the loan VaR is higher when
is enhanced, the loan VaR is higher when![]() , whereas lower if
, whereas lower if![]() , that means, to some extent, higher h can lower loan VaR if LTV is set at a high level by the bank.
, that means, to some extent, higher h can lower loan VaR if LTV is set at a high level by the bank.
4.2.2. Impact of q and vmin
Instead of limiting the order quantity q, LTV was set as an limit to prevent the bank from loan risk. As a matter
![]()
Table 2. Impact of h and vmin on the Critical Value of LTV and Extreme Value of loan VaR When q = 10, mu = 4 and T = 6.
of fact, the bank generally has no ability to control the borrower’s order quantity, which may have an influence on the loan VaR. Let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , then
, then![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() is unchanged because h,
is unchanged because h, ![]() , p and
, p and ![]() are constant. As analyzed in 4.2.1, the loan VaR will be notably increasing if
are constant. As analyzed in 4.2.1, the loan VaR will be notably increasing if ![]() when q is constant such as
when q is constant such as![]() . On the contrary, the loan VaR will has a decrease if q increases from 10 to 20 whether
. On the contrary, the loan VaR will has a decrease if q increases from 10 to 20 whether ![]() or not, just like the Table 3 shows.
or not, just like the Table 3 shows.
Furthermore, Figure 4 clearly illustrates the variations of loan VaR as q and ![]() changing. Notably, the values of loan VaR are negative companion with the increasing of q from 10 to 20 when
changing. Notably, the values of loan VaR are negative companion with the increasing of q from 10 to 20 when![]() , that means, the more q, the lower the risk if
, that means, the more q, the lower the risk if ![]() is higher than p under the situation of the whole order quantity are needed on the commodity markets.
is higher than p under the situation of the whole order quantity are needed on the commodity markets.
4.2.3. Impact of T and m
T and ![]() respectively denotes the loan period and one of the parameters of log-normal distribution of retailer’s demand
respectively denotes the loan period and one of the parameters of log-normal distribution of retailer’s demand![]() , since
, since![]() , according to Lemma 4, then
, according to Lemma 4, then ![]() is given by
is given by
![]()
As an example, let![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . As Table 4 shows,
. As Table 4 shows, ![]() ,
, ![]() and
and ![]() will respectively decrease with 39.35% ((0.8298 − 0.5033)/0.8298 * 100%),
will respectively decrease with 39.35% ((0.8298 − 0.5033)/0.8298 * 100%),
(a) ![]() (b)
(b) ![]()
Table 3. (a) Impact of q and vmin on the critical value of LTV and extreme value of loan VaR when h = 10, mu = 4 and T = 6; (b) Impact of q and vmin on the critical value of LTV and extreme value of loan VaR when h = 15, mu = 4 and T = 6.
51.84% ((4.1276 − 1.9879)/4.1276 * 100%) and 31.03% ((6.8954 − 4.7557)/6.8954 * 100%), companion with the increase of ![]() from 3 to3.5 when
from 3 to3.5 when![]() , which illustrates that
, which illustrates that ![]() is negative with the loan VaR and
is negative with the loan VaR and![]() .On the contrary, the values of
.On the contrary, the values of ![]() and
and ![]() increase when T increase from 3 to 9 if
increase when T increase from 3 to 9 if ![]() remains to 3 or 3.5, which denotes that the values of loan VaR are positive with T under a certain LTV.
remains to 3 or 3.5, which denotes that the values of loan VaR are positive with T under a certain LTV.
Furthermore, as in Figure 5, when![]() , the values of loan VaR with
, the values of loan VaR with ![]() are higher than that with
are higher than that with![]() , specifically, higher at
, specifically, higher at ![]() than that at
than that at![]() , however, when
, however, when ![]() or
or![]() , the values of loan VaR with
, the values of loan VaR with ![]() are lower than that with
are lower than that with![]() , which illustrates that it’s better to choose value of LTV ranging from 0.1 to 0.5 or 0.82 to 1.00 with shorter loan period T and
, which illustrates that it’s better to choose value of LTV ranging from 0.1 to 0.5 or 0.82 to 1.00 with shorter loan period T and![]() , whereas the range of 0.50 to 0.82 is better with relatively longer T and higher
, whereas the range of 0.50 to 0.82 is better with relatively longer T and higher![]() , from the perspective of loan VaR. In any case, longer loan period leads to higher loan VaR with the certain LTV.
, from the perspective of loan VaR. In any case, longer loan period leads to higher loan VaR with the certain LTV.
5. Conclusions
In this paper, the problem of the relationship between LTV and loan VaR was dealt with to explore the critical LTV that could affect the extreme values of loan VaR, which was the worst potential loss of the loan causing by LTV decisions and price-decline of the inventory pledged in commodity market. Although several literatures concentrate on the issue of LTV decisions in inventory financing of SCF or the applications of VaR method, there are few studies focusing on the relationship between LTV and loan VaR, meanwhile, considering the borrower’s positions of financial and procurement.
Firstly, we assume that the borrower’s demand follows generally distribution, followed by the general conditions of linear and nonlinear relationships between LTV and loan VaR, as well as the critical order quantity in linear analysis and the critical values of LTV corresponding to extreme values of loan VaR in nonlinear analysis, meanwhile, the log-normal distribution of the borrower’s demand was assumed based on the general model, with the specific results and conclusions. Moreover, the critical order quantity follows the established linear relationship and has an influence on the monotonic property of loan VaR to LTV. In particular, the loan VaR is positive with LTV as the real order quantity is less than the critical value, whereas, with negative value and is negative with LTV, that is, the higher quantity the borrower orders, the lower loan VaR the bank will suffer under the precondition of no order which limits to the borrower. In addition, the initial wealth of the retailer merely influences the loan risk level relative to LTV, as a matter of fact, both ![]() and q mainly influence the VaR level of the loan.
and q mainly influence the VaR level of the loan.
However, the problems of setting loan margin, setting the proportion of inventory pledged to total purchase amount, choosing semi-finished product as inventory pledged and LTV decisions of the bank with an attitude of risk-neutral in inventory financing of SCF were not analyzed in this paper, and the following problems would be fatherly considered, including 1) Consider the first order and second order conditions with the proportion determine the loan margin; 2) Multiply the proportion of inventory pledged to total purchase amount as calculating the loan amount; 3) Consider the buy-back decisions to the collateral with semi-product, which has a high level
of specificity and weaken liquidity in commodity market; 4) Further considering the bank with risk-neutral attitude with an objective of profit-maximization.
Acknowledgements
The authors would like to thank the support by Project of Outstanding Young Teachers’ Training in Higher Education Institutions of Guangxi and a grant of Guangxi Philosophy and Social Science Fund (13BGL009).