
Subject Area: Theoretical Physics

1. Introduction
Considering the magnificent success of the “Standard Model” in describing the existence and interactions of the incredible zoo of elementary and composite quantum particles that inhabit (or can be forced to materialize in) our universe, it is very difficult to imagine that there is anything in physics that has been misunderstood. Nevertheless, regarding the most fundamental elements of gravitation theory, serious errors have persisted for over a century. This is understandable in view of the fact that the editors of physics journals must deal with a flood of submissions by “cranks” who characteristically address issues that mainstream physicists consider to be settled once and for all, having been so thoroughly studied by the dominant physics community that no further discussions need to be considered. In fact, it is my experience that any submission addressing any one of these settled issues will be rejected out of hand without any real review, even unread. But certain of these issues have actually not received careful consideration, with the result that several incorrect concepts in the theory of gravitation are protected as settled issues, allowing errors to survive, even for a century. The purpose of this paper is to identify some of these errors, to show how they enter the theory, and to present a new interpretation of Einstein’s 1916 theory of gravity1 based upon the concept of variable rest mass.
2. Einstein’s 1911 Paper: The Equivalence Principle and Its Implications
A brief review of the history of the development of Einstein’s theory of gravity will reveal how certain errors regarding the interpretation of the theory entered mainstream thinking. The most egregious error was, and is, the failure of Einstein and his followers to attempt to discover the cause of the gravitational red shift. This phenomenon was predicted by Einstein in a very remarkable 1911 paper [1] . In this paper Einstein boldly proposed his now famous principle of equivalence, according to which acceleration is equivalent to gravity: thus, for instance, experiments conducted in a rocket ship accelerating in the absence of gravity at one “g”, are predicted to give results identical to the same experiments conducted on the surface of the earth, where the acceleration of gravity has the same value. According to the well-understood Doppler Effect, a continuous single-frequency light signal sent “upward” in the accelerating rocket ship will be measured by the receiver to be reduced in frequency (red- shifted) because the receiver will have a higher velocity when the signal arrives than the emitter had when it launched the signal. Applying his new principle of equivalence, Einstein immediately inferred the existence of a gravitational red shift effect: light sent upward in a gravitational field would be received red shifted as compared with the emitted frequency2. Straightaway, Einstein noted that this seemed to imply an absurdity: if fewer wavecrests are received above than are emitted below, the number of wavecrests in between would continually increase, contrary to the assumption of time-independence. Einstein settled this issue by asserting that there is no reason to assume that clock rates are not influenced by gravity. He postulated that clock rates are reduced by the
factor  which reduction3 causes of frequency measurements be exaggerated by the inverse factor:
which reduction3 causes of frequency measurements be exaggerated by the inverse factor: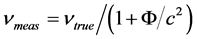 . Regarding the red shift one has
. Regarding the red shift one has , where
, where 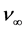 is the emission frequency in the absence of gravity, and
is the emission frequency in the absence of gravity, and 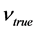 is the true frequency in flight, a constant. Finally,
is the true frequency in flight, a constant. Finally, 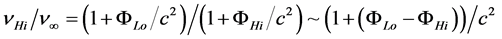 , Einstein’s result.
, Einstein’s result.
Surprisingly, Einstein did not attempt to understand the cause of this clock slowing effect?his immediate concern was that slowing clock rates would (and here he made an unwarranted assumption?that distance measurements would not be influenced by gravity) cause local observers to overvalue the speed of light?contrary to an enshrined principle of special relativity, that all observers will measure the speed of light to be the same universal constant. Incredibly, Einstein immediately jumped to the conclusion that the true speed of light must be reduced by gravity so as to insure that the locally measured speed of light be constant. One can only marvel at the remarkable philosophical flexibility exercised by Einstein in this matter. Regarding the reduction of the speed of light, Einstein seems to have imagined that the gravitational field possessed an effective index of refraction. In contrast, modern theorists attribute the effect to the rather mystical idea that the flow of time itself is reduced by gravity4, thus “explaining” not only light’s speed reduction, but also the slowing of clocks. In any event, it did not occur to Einstein, nor has it occurred to a century of his followers, that perhaps the measurement of distances might be influenced by gravity.
3. Bohr’s Paradigms for Length & Time Intervals:  &
& 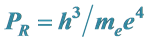
The answers to these unasked questions were not long in coming, but they were ignored. In 1913 Niels Bohr put forward his quantum theory of the hydrogen atom [2] . Bohr’s primitive theory has been supplanted by ever more sophisticated treatments, but Bohr did give us paradigms for time and distance intervals: what may be called the Rydberg period,  , and the Bohr radius,
, and the Bohr radius,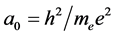 .
.
The frequencies emitted by every atomic species are determined by a formula involving species-specific quantum numbers, but in every case the leading factor in the formula is the reciprocal of the Rydberg period, PR. This formula holds regardless of the location of the atom in a gravitational field. Of course, all quantities of the same kind, i.e., of the same dimensionality, must vary together, so all masses must be similarly reduced. Thus, as early as 1914, the cause of the gravitational red shift might have been understood to be the decrease of rest masses in a gravitational field. Also, considering that the Bohr radius is inversely proportional to me, it is clear that in a gravitational field, measuring rods will be elongated, so that distance measurements will be underestimated by the same factor as clock rates are slowed, guaranteeing that any local measurement of the speed of light will be unaffected by gravity. This restores the invariance of the true speed of light, and demolishes the idea that the flow of time itself is reduced by gravity.
4. The True Nature of Gravitational Potential Energy
This phenomenon, gravitational rest mass reduction, is easily understood in terms of the celebrated equation, : when a mass is raised against gravity, the increase in potential energy, Δw, is stored in the body itself as an increase in rest mass:
: when a mass is raised against gravity, the increase in potential energy, Δw, is stored in the body itself as an increase in rest mass: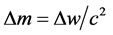 . Unfortunately, this simple idea runs counter to one of the settled issues of physics. Before there was any hint of the connection between mass and energy, the consensus was that gravitational potential energy resided in the gravitational field itself. Awkwardly, since the absolute value of gravitational field strength increases as gravitating masses are brought together, this model, in order to account for the attractive nature of gravity, required that the energy density of the gravitational field must be negative! Fortunately, this difficult concept may be safely discarded since there is a simple thought experiment proving that rest masses are reduced in a gravitational field, in accord with the variable rest mass interpretation of gravitational potential energy.
. Unfortunately, this simple idea runs counter to one of the settled issues of physics. Before there was any hint of the connection between mass and energy, the consensus was that gravitational potential energy resided in the gravitational field itself. Awkwardly, since the absolute value of gravitational field strength increases as gravitating masses are brought together, this model, in order to account for the attractive nature of gravity, required that the energy density of the gravitational field must be negative! Fortunately, this difficult concept may be safely discarded since there is a simple thought experiment proving that rest masses are reduced in a gravitational field, in accord with the variable rest mass interpretation of gravitational potential energy.
5. Positronium Proof of Gravitational Rest Mass Reduction
Consider the annihilation of a ground-state para-positronium system deep in a time-independent gravitational field. In this process, the entire combined rest mass of the electron and the positron will be converted to gamma ray photons. In a time-independent field, energy is conserved [3] , so the photons will move upward with constant energy. Nevertheless, because of the gravitational red shift, the total energy of the photons emitted from the annihilation event will be measured by distant observers, who are unaffected by the field, to be reduced as compared with the rest mass energy of such a system measured locally by these observers. The unavoidable conclusion is that the rest mass of the positronium system was reduced by the action of the gravitational field, upsetting another of the settled issues of physics, namely, that rest mass is unaffected by gravity.
6. Gravity Converts Rest Mass Energy to Kinetic Energy and Vice Versa
Crucially, there in an equation of motion ( [4] , p. 292) for a test mass moving freely in a time-independent field of gravity: it expresses the conservation of energy:
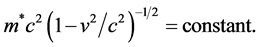
Here 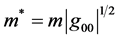 is the true rest mass, m is the proper rest mass, a constant, and g00 is the time-time component of the metric tensor
is the true rest mass, m is the proper rest mass, a constant, and g00 is the time-time component of the metric tensor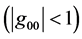 , a function of position, that characterizes the gravitational field. Sig-
, a function of position, that characterizes the gravitational field. Sig-
nificantly, energy conservation is expressed here as a product, rather than a sum. The equation implies that gravity converts rest mass energy to kinetic energy and vice versa. An obvious inference is that any change in the gravitational potential energy of the test mass exists as a change in its rest mass energy: no energy is stored in the gravitational field.
7. Gravity Couples Exclusively to Rest Mass
This suggests, as will be further argued below, that gravity couples exclusively to rest mass. This fact is of inestimable importance, since it undermines another settled issue, namely, that every element of the stress-energy tensor contributes to the gravitational field. In particular, freely moving5 massless quanta such as photons and gravitons are presently thought to contribute to the gravitational field and to be affected by it. The experimental evidence supporting this concept is the observation of the “bending of light rays” by the gravitational field, first observed during the eclipse of May 1919 by teams organized by Frank Dyson and Arthur Eddington. More accurate modern observations corroborate the fact that indeed light does not follow the spatial geodesics of the proper non-Euclidean geometry inherent to the gravitational field.
But in view of rest mass reduction, Bohr’s expression for the radius of the hydrogen atom, 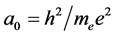 , implies that the radius of the hydrogen atom (and of all other lengths, including that of measuring rods), will be dilated in a gravitational field. This means that the currently accepted proper geometry in the vicinity of a gravitating body is incorrect. Correcting for this effect gives rise to a new, correct geometry, in which light rays do follow geodesics paths (the straightest paths possible in a non-Euclidean geometry), as will be shown directly.
, implies that the radius of the hydrogen atom (and of all other lengths, including that of measuring rods), will be dilated in a gravitational field. This means that the currently accepted proper geometry in the vicinity of a gravitating body is incorrect. Correcting for this effect gives rise to a new, correct geometry, in which light rays do follow geodesics paths (the straightest paths possible in a non-Euclidean geometry), as will be shown directly.
8. Gravitational Size Dilation and the New Geometry
Besides finally revealing the true nature of gravitational potential energy, rest mass reduction is the key to understanding and correcting a long-standing error regarding the geometry of three-dimensional space in a gravitational field. The metric for a time-independent central gravitational field will always feature a position-depen- dent time-time component, g00, of absolute value less than unity, that gives rise to the acceleration of gravity, to the gravitational red shift, and to the size dilation of all material objects, including measuring rods.
Because of the latter effect, the proper metric for the three dimensional geometry of space, 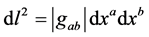 , must be considered to be defective, since distances are underestimated by the factor
, must be considered to be defective, since distances are underestimated by the factor![]() . The true geometry is then is described by the correct spatial metric, namely,
. The true geometry is then is described by the correct spatial metric, namely,![]() .
.
Regarding the bending of light rays, the path followed by a light ray may be determined from the proper metric, ![]() , by setting
, by setting![]() , whence
, whence![]() . Then, according to
. Then, according to
Fermat’s principle of least time, the ray path may be found by minimizing the integral of ![]() between specified end points. But this is same as finding the path of minimum distance, the geodesic path, in the correct spatial metric,
between specified end points. But this is same as finding the path of minimum distance, the geodesic path, in the correct spatial metric,![]() . Thus light rays are merely following the geodesics (the straightest possible paths) of the correct geometry. This result is in line with the fact that in a time-independent field, light moves with constant energy, indicating again that there is no coupling of gravity to the free electromagnetic field.
. Thus light rays are merely following the geodesics (the straightest possible paths) of the correct geometry. This result is in line with the fact that in a time-independent field, light moves with constant energy, indicating again that there is no coupling of gravity to the free electromagnetic field.
9. Optical Geometry
Interestingly, the identical geometry has been proposed on the basis of an important discovery regarding the kinematics of massive bodies in a gravitational field. Abramowicz et al. [6] proved that in a static gravitational field, a body will not experience speed-dependent forces (centrifugal and Coriolis forces) if it is constrained to move along a path that a light ray might follow. By analogy to Newtonian mechanics, in which such forces vanish for bodies moving in straight lines, the authors defined a new geometry by identifying light rays as the geodesics of the new geometry, which they named, appropriately, “Optical Geometry”.
10. Quantum Implications: Saving the Spin-Zero Graviton
By far the most important consequence of this heretofore unsuspected phenomenon, gravitational size dilation, is its implications regarding quantum gravity. The “bending of light rays”, i.e., the failure of light rays to follow the geodesics of the (incorrect) proper geometry, has been used to rule out the spin-zero graviton, since spinless quanta can only couple to the trace of the energy-momentum tensor of the target field, and the energy-momen- tum tensor of the free electromagnetic field has a zero trace. But light rays do follow the geodesics of the correct geometry, so theorists have wrongly rejected the spin-zero graviton, which should be accepted, and wrongly accepted the spin-two graviton, which should be rejected, at least as the quantum manifestation of gravity as a static field.
It has been shown that gravitational fields arise solely from sources having rest mass, and that gravity couples only to rest mass. Gravitons thus do not act as sources of gravity; they are not affected by gravity; and they do not interact with one another. In this respect, the situation is analogous to the relation of photons to the electromagnetic field and to one another. Within the same analogy, rest mass acts as the “charge” for the gravitational field. But the analogy breaks down since electric charge is invariant and the electromagnetic field possesses energy, whereas in the case of gravity, potential energy resides not in the field, but rather in the variable rest mass energy of the “charges”.
The fact that gravitons interact neither with the field itself, nor with one another, eliminates dreaded non-li- nearities, and gives promise of a linear, spin-zero scalar theory―a radical and welcomed simplification of the problem of formulating a quantum theory of gravity.
11. The Implications of Variable Rest Mass in the Theory of Black Holes
Variable rest mass also has important consequences regarding the theory of black holes and cosmology. Regarding black holes, we restrict our attention to the Schwarzschild field. The proper metric may be written:
![]()
Since, as argued above, proper time intervals and distance intervals are underestimated by the same factor, f, the correction is effected by multiplying by![]() . Thus the correct metric, the variable rest mass (VRM) metric, is
. Thus the correct metric, the variable rest mass (VRM) metric, is
![]()
Note that this metric does not represent a solution to the field equations: it simply introduces a system for the measurement of time and distance that is not influenced by the field. Time is measured using signals from a remote clock (the “clock at infinity”), while distances are measured by electromagnetic echo ranging calculated using the same time system6.
Before considering how the true geometry of a black hole is revealed in the VRM interpretation, a review of Schwarzschild static black hole structure according to the mainstream interpretation seems appropriate. The basic structure is a singularity hidden behind a surface called the event horizon, from which the escape velocity is equal to the speed of light. This surface is very special in that light sent from a finite proper distance directly toward the event horizon never reaches that surface. Proponents of the accepted interpretation “explain” that because of “the slowing of the flow of time itself”, the speed of light goes to zero as light approaches the event horizon, i.e., ctrue → 0 as r → rS.
Another puzzling fact is that light does not follow the geodesics (shortest paths) of the proper geometry. Again, proponents “explain” that the speed of light is greater along a path outside of the proper geodesic path, where there is less “slowing of the flow of time itself”. But, as argued in Appendix I, the claim that light’s speed is reduced by a factor f in a gravitational field also requires, unacceptably, that Planck’s constant and rest masses increase by factors of ![]() and
and ![]() respectively. Another mystery concerns the behavior of centrifugal force. According to the proper metric, every sphere centered on a black hole is convex when viewed from the outside, except for the event horizon itself, which, in the proper metric, appears to have zero curvature. Nevertheless, for any location inside the locus of photon orbits at 3/2rS, centrifugal force acts inwardly! Clearly, this phenomenon, the Abramowicz Effect [7] [8] cannot be accounted for in the context of the proper geometry of the conventional interpretation.
respectively. Another mystery concerns the behavior of centrifugal force. According to the proper metric, every sphere centered on a black hole is convex when viewed from the outside, except for the event horizon itself, which, in the proper metric, appears to have zero curvature. Nevertheless, for any location inside the locus of photon orbits at 3/2rS, centrifugal force acts inwardly! Clearly, this phenomenon, the Abramowicz Effect [7] [8] cannot be accounted for in the context of the proper geometry of the conventional interpretation.
The puzzling phenomena that appear in the conventional interpretation are easily understood in terms of the VRM interpretation. First of all, the geometry is very different. In the VRM metric, the area of a centered sphere
is equal to![]() . Differentiating with respect to r, one has
. Differentiating with respect to r, one has
![]()
Thus the area of a sphere is not a monotone function of r: it has a minimum at![]() , the locus of photon orbits. Furthermore, for
, the locus of photon orbits. Furthermore, for![]() , the area of a sphere increases without limit as r approaches rS. The sphere of minimum area, the stenosphere, is the throat of a wormhole-like structure connecting our familiar universe to another infinite three-space, which may reasonably be called “innerspace”. In the VRM metric, the stenosphere has zero curvature, which explains why centrifugal force vanishes there. This vanishing, in turn, confirms the fact that photons do not feel the force of gravity, since on the stenosphere there can be no centrifugal force to counter an imagined force of gravity acting on photons.
, the area of a sphere increases without limit as r approaches rS. The sphere of minimum area, the stenosphere, is the throat of a wormhole-like structure connecting our familiar universe to another infinite three-space, which may reasonably be called “innerspace”. In the VRM metric, the stenosphere has zero curvature, which explains why centrifugal force vanishes there. This vanishing, in turn, confirms the fact that photons do not feel the force of gravity, since on the stenosphere there can be no centrifugal force to counter an imagined force of gravity acting on photons.
Note that inside the stenosphere, the surface of a centered sphere, viewed from the “outside,” will be concave rather than convex. Thus, regarding the Abramowicz Effect, the correct geometry shows that the direction of centrifugal force obeys the usual pattern inside the stenosphere: the force is directed from the concave side to the convex side of the circle on which a body is constrained to move.
Regarding the other puzzles, it is obvious that light cannot reach the event horizon since that surface is infinitely distant in “innerspace” (the seeming finite proper distance to that surface is an artifact of the limitless elongation of measuring rods as r → rS). That proper geodesics lie inside VRM geodesics is easily understood: proper geodesics ‘cheat’ by taking advantage of the elongation of measuring rods implied by the gravitational size dilation effect. Another significant feature of the VRM interpretation is the non-existence of the baleful singularity, which, according to the usual interpretation, is thought to lurk behind the event horizon.
12. Looking Back: At the Fundamental Level, Is Gravity a Field Theory?
In retrospect, the concept of gravity presented here is clearly more in line with Newton’s (self-berated) action-at-a-distance formulation, than with Einstein’s field theory. Indeed, what role is left for the field if gravitational ‘charges’ (masses) are capable of exchanging momentum and energy directly? The role of the gravitational field is further diminished by the fact that any truly tensorial formulation of an energy-momentum tensor of the gravitational field itself in Einstein’s theory of gravity must be identically zero, since the field and the proposed energy-momentum tensor will vanishes locally in any freely-falling frame of reference. The tensor character then guarantees that the proposed energy-momentum tensor vanishes in every frame of reference. Another disturbing feature of gravity is that, as a practical fact, the force of gravity acts instantaneously. Of course, such instantaneous action is untenable unless a preferred frame of reference, the aether, actually exists. Surprisingly, a proof of aether’s existence is possible even though the proof requires acceptance of the relevance of a universe having the topology of a flat three-torus. In this imagined universe, attempts to set clocks according to Einstein’s scheme along each of the four shortest geodesic paths connecting the master clock with the clock to be set will usually yield inconsistent settings. But, as detailed in Appendix III, the data recorded in these attempts may be used to identify an aether frame in which all clocks can be unambiguously set.
Despite these facts, which would seem to render the gravitational field almost irrelevant, it must be recognized that the non-Euclidean geometry of three-space inherent to the gravitational field is indispensible to the correct understanding of the dynamical behavior of both massive particles and light, as well as the structure of black holes. The problem remaining is to discover how the presence of mass induces such profound changes in the geometry of three-space. But underlying all, the field seems somehow responsible for the reduction of rest masses, which is the cause of the two fundamental gravitational phenomena: gravitational clock slowing (the red shift) and gravitational size dilation.
13. The Implications of Variable Rest Mass for Cosmology
The most surprising implication of the variable rest mass concept relates to cosmology. Hubble’s discovery of the systematic cosmological red shift immediately suggested that galaxies were flying through space away from us and from one another―the further, the faster. This in turn suggested that the universe grew from an incredibly hot and dense condition (a singularity!) billions of years ago. Later, solutions of the field equations revealed that the galaxies were not actually moving through space, but rather that space itself was expanding. The conventional understanding holds that the wavelength of light is continually stretched in flight by the expansion of space. Thus in the present understanding, the redshift parameter, ![]() , shown by a galaxy is held to be proportional to the ratio of the scale of the present universe to that of the universe at the time of emission.
, shown by a galaxy is held to be proportional to the ratio of the scale of the present universe to that of the universe at the time of emission.
Neither astronomers nor cosmologists seem to be concerned with the fact that this explanation of the cosmological red shift fails to conserve the momentum of the observed radiation, as Noether’s Theorem demands in a spatially homogeneous universe [3] . Observation shows that, on a sufficiently large scale, the universe is homogeneous and isotropic to a very high degree, and virtually every cosmological model assumes this at the outset. Perhaps no one has even considered this problem since, as every observation of the red shift appears to have demonstrated, momentum seems to be manifestly not conserved. The photons of the cosmic microwave background radiation field that we detect today were born in a 3000˚K hydrogen-helium plasma at “recombination” time, when the plasma first became transparent. Their wavelength has seemingly increased by a factor of about 1000?how is it possible that their momentum has not changed? The only possibility is that over the aeons, measuring instruments have changed, and are changing, decreasing their characteristic wavelengths?for example, diffraction gratings have shrunk and are shrinking. And the only way this might occur is if all rest masses have been and are increasing in proportion to![]() , in which A(t) is the function that is presently interpreted as representing the increasing scale of the universe, and
, in which A(t) is the function that is presently interpreted as representing the increasing scale of the universe, and ![]() is its present value.
is its present value.
To prove that momentum conservation requires rest masses to increase in proportion to a(t), one need only consider the motion of a test mass through space. In this case, there is an integral of motion (developed in Ap-
pendix II) for the Robertson-Walker metric, namely,![]() . Since the momentum is given by
. Since the momentum is given by![]() , it is clear that conservation of momentum requires that the true rest mass, m*, must be proportional to a(t), that is,
, it is clear that conservation of momentum requires that the true rest mass, m*, must be proportional to a(t), that is, ![]() where m is the proper rest mass, a constant.
where m is the proper rest mass, a constant.
A very elaborate calculation is required to solve the field equations for cosmology under the assumption that momentum is conserved ( [5] , pp. 71-76). The surprising result is that a(t) turns out to be a simple exponential function of world time. But upon thoughtful reflection, it is obvious (in hindsight) that such must be the case, as will now be shown.
14. An Easy Proof That Rest Mass Increases Exponentially with World Time
Consider a source of monochromatic light and two observers lying on a straight line at distances d1 and d2 > d1 from the source. Generally,![]() . Let λ1 & λ2 be the wavelengths observed at d1 & d2, at times t1 & t2. In the case considered,
. Let λ1 & λ2 be the wavelengths observed at d1 & d2, at times t1 & t2. In the case considered,![]() .
.
Momentum conservation implies that the wavelength of light remains constant in traveling between any two points. If that is so, the spectra measured at d2 will differ from that observed at d1 only as a result of the changes in the instruments at d2 caused by the general increase in rest masses during the time interval![]() . And of course, the same is true for the time interval
. And of course, the same is true for the time interval![]() . Thus the function on the right hand side above must
. Thus the function on the right hand side above must
be representable as the product of some function, u , of d1/c and the same function of![]() , i.e.,
, i.e.,![]() . But when d2 = d1, we must have u = a. Thus the function a satisfies the relation
. But when d2 = d1, we must have u = a. Thus the function a satisfies the relation![]() . Only the exponential function satisfies this functional equation, so
. Only the exponential function satisfies this functional equation, so![]() , the form being chosen so that a(tnow) = 1.
, the form being chosen so that a(tnow) = 1.
The frequency parameter, ω, is easily identified as the Hubble constant, H0. For nearby galaxies, Hubble’s “law” implies![]() . The exponential function gives
. The exponential function gives ![]() , for nearby galaxies. Thus, ω = H0. Regarding the evolution of proper time, T,
, for nearby galaxies. Thus, ω = H0. Regarding the evolution of proper time, T, ![]() , so
, so ![]()
Thus the rest mass evolution function is a linear function of proper time, T.
15. The Two Times
Proper time is that kept by physical clocks whose rates, looking backward in time, slow in proportional to a(t). World time, t, may be thought of as being defined with reference to any observable free electromagnetic radiation―in particular, the cosmic microwave background radiation?whose true frequency is constant. Paradoxically, it is quite clear that the universe is infinitely old in terms of world time, t: yet it is no less true that the universe suddenly came into existence with a “Big Bang” some H0−1 seconds (~14 billion years) ago in terms of proper time, T.
16. Other Studies Proposing the Cosmological Evolution of Rest Mass
Others have proposed cosmologies in which rest mass evolves with time, notably Hoyle and Narlikar [9] ; Narlikar [10] ; Narlikar and Arp [11] ; and more recently, Wetterich [12] . But in each case, the variable rest mass concept was introduced ad hoc―not in order to satisfy the conservation of momentum demanded for a homogeneous universe.
17. Prospects for the Acceptance of the Evolving Rest Mass Cosmology
The evolving rest mass interpretation of the cosmic red shift has not been widely accepted, to say the least. The idea that the universe is not expanding but has evolved from a state (infinitely long ago in terms of world time) in which all fields were massless is very far from mainstream thinking and will be extremely hard for the physics community to accept. Nevertheless, it is the only cosmology satisfying the requirement of momentum conservation. Also, this cosmology does have several attractive features?there is no singularity, uniformity and smoothness are guaranteed by the very slow (with respect to world time, t) development of rest mass, and temperatures (as assessed in the VRM reference frame) are for all times past only modestly higher than present values ( [5] , p. 78). Importantly, it should be easy to make a decision regarding the acceptance of the VRM cosmology since the theory makes the very definite prediction that the mass evolution function, a(t), must be a simple exponential function of world time t, or, equivalently, a linear function of proper time, T.
18. Afterword
The variable rest mass concept underlies every one of the transformative ideas presented in this paper. It seems almost impossible that the physics community has for over a century failed to identify rest mass reduction as the cause of the gravitational red shift. It would appear that the discovery of causes and the seeking of understanding are no longer considered important, since special relativity and quantum theory especially are manifestly counterintuitive. This may also account for the extraordinary array of unwarranted assumptions which persist in the theory of gravity. I believe that these aberrations can be traced back to Einstein’s aetherless re-interpretation of the relativity theory developed by Lorentz, Poincaré and Larmor, which was already fully developed in terms of the luminiferous aether, and was published before Einstein’s 1905 paper appears.
Regarding Einstein’s paper, physicists evidently fail (and continue to fail) to realize that the magical constancy of the measured speed of light is a simple consequence of Einstein’s system for setting clocks: a system based on Einstein’s definition (!!) that the time required for a light signal to go from A to B is equal to that required to go from B to A. In fact, light’s measured speed is constant as a tautological consequence of the method prescribed for setting clocks! Without this understanding, Einstein’s special relativity is literally incomprehensible. Thus regarding two systems in relative motion, each system will observe the other’s clock rates to be slowed and measuring rods to be shortened. Such seeming paradoxes can be fully understood in terms of the aether ( [5] , 18-20), but for those rejecting the aether concept, such paradoxes can only be humbly accepted.
Einstein’s version of special relativity received universal acceptance, and the aether concept was relegated to the trash bin of superfluous ideas. If the existence of a privileged aether frame of reference is denied, every system has its own equally valid time, with the consequence that the order in which events occur is ambiguous: in one system, event X precedes event Y, but in another system, Y precedes X. This erosion of the concept of cause and effect, along with several seeming paradoxes, appears to have undermined physicist’s belief in the very possibility of understanding phenomena. Today any attempt to explain a phenomenon (for example, the gravitational red shift) will be rejected with condescension, and a reminder that “the mathematics says it all”.
Curiously, this rejection of the possibility of true understanding has led to the easy acceptance of ideas that border on, or even cross the border of, what may fairly be called unreasonable. Foremost among these is the relativity of time, asserting that the flow of time itself depends upon an observer’s motion and location in a gravitational field. Other such ideas include Kip Thorne’s proposal for time travel to the past, Hugh Everett’s many worlds resolution of Schrodinger’s cat paradox, Alan Guth’s cosmic inflation to account for the uniformity and flatness of the universe, and finally Brandon Carter’s anthropic explanation for the fine tuning of physical constants, an argument that necessarily posits an infinity of universes, among which at least one possesses a set of physical constants consistent with the development of life.
All this philosophical relativism began with Einstein’s rejection of a preferred frame of reference, the aether, without which there was no universal ordering of events, and hence no unambiguous assignment of cause and effect―a concept absolutely vital to the realist point of view, which had been, and should remain, the basis of all scientific endeavors. It is in support of this realist philosophy that I have presented in Appendix III my rather whimsical proof of aether’s existence.
Appendix I
It is proved that rest mass reduction is necessary and sufficient to account for the gravitational red shift in a manner that preserves the invariance of the measured speed of light and reveals the correct geometry of space in the neighborhood of a gravitating body. Consideration of the Strong Equivalence Principle (SEP) will guide our search for the cause of the reduction of emission frequencies in a gravitational field. According to Richard Dicke [13] , the SEP asserts that
In a freely falling, non-rotating laboratory, the local laws of physics take on some standard form, including a standard numerical content, independent of the position of the laboratory in space and time.
Many modern-day physicists misunderstand this as implying that nothing can actually change in the laboratory as it falls in a real gravitational field. This certainly is not the case since, as we already know, clock rates are slowed. The SEP only requires that any changes must occur in concert so as to be undetectable by observers in the falling lab. One thing the SEP certainly demands is that quantities of the same dimensionality must vary together, if they do vary, by exactly the same factor. Thus all quantities having the dimension of time must vary exactly as does the Rydberg period, PR, and all quantities having the dimension of length must vary as does the Bohr radius, a0. Going Further, all quantities having the dimension of velocity must vary as![]() . This must apply to the velocity of light, so it must be true that
. This must apply to the velocity of light, so it must be true that ![]() is unaffected by gravity. But this is just the fine structure constant, which is an observed constant, not just in Dicke’s falling lab, but as observed for instance in the spectra of distant stars.
is unaffected by gravity. But this is just the fine structure constant, which is an observed constant, not just in Dicke’s falling lab, but as observed for instance in the spectra of distant stars.
We are now in a position to summarize what we know regarding the possible dependence of the “constants” upon the gravitational potential. First, there is a red shift, implying that![]() , where
, where![]() . In
. In
what follows the dependence of any quantity, X, on f will be indicated by writing X ~ f (X). Accordingly, the red shift implies![]() . This may be expanded to
. This may be expanded to![]() . Next,
. Next,![]() . Finally, from the finding regarding the fine structure constant, we have
. Finally, from the finding regarding the fine structure constant, we have![]() . Clearly, these equations are satisfied by
. Clearly, these equations are satisfied by![]() ,
, ![]() ,
, ![]() , implying
, implying![]() , and
, and![]() . These relations characterize the variable rest mass (VRM) interpretation of gravity. Of course, according to the SEP, if the electron rest mass, me, is reduced, all masses are similarly reduced. For the same reason, the increase of a0 implies that the dimension of all objects, including measuring rods, is increased, and the increase in PR implies that all time periods are similarly increased (or, what is the same thing, frequencies are decreased by the reciprocal factor).
. These relations characterize the variable rest mass (VRM) interpretation of gravity. Of course, according to the SEP, if the electron rest mass, me, is reduced, all masses are similarly reduced. For the same reason, the increase of a0 implies that the dimension of all objects, including measuring rods, is increased, and the increase in PR implies that all time periods are similarly increased (or, what is the same thing, frequencies are decreased by the reciprocal factor).
Following Einstein [1] , modern day physicists have unconsciously assumed that that distance measurements are unaffected by gravity, implying![]() . Then since
. Then since![]() , it would follow that
, it would follow that![]() . But from the original definitions,
. But from the original definitions, ![]() , which is equal to (c). This would imply that
, which is equal to (c). This would imply that![]() , just
, just
as Einstein had assumed in order that the locally measured speed of light be independent of location in a gravitational field. The same equation, ![]() , would then imply that
, would then imply that![]() . Next, inserting this into the original equation for (a0), and setting
. Next, inserting this into the original equation for (a0), and setting ![]() would give
would give![]() . But charge invariance implies
. But charge invariance implies![]() , so that finally, Einstein’s assumption that distance measurements are unaffected by gravity requires not only that
, so that finally, Einstein’s assumption that distance measurements are unaffected by gravity requires not only that![]() , but also that
, but also that![]() , and
, and![]() . Mainstream physicists will perhaps be surprised and puzzled by the full implications of Einstein’s seemingly necessary and harmless assumption regarding the speed of light in a gravitational field. Notice that the correct choice implies that measuring rods are elongated, so that distance measurements are undervalued by the same factor as clock rates are slowed, guaranteeing that local measurements of the speed of light are unaffected by gravity. And of course the presently accepted idea that the true speed of light is reduced in a gravitational field must be rejected.
. Mainstream physicists will perhaps be surprised and puzzled by the full implications of Einstein’s seemingly necessary and harmless assumption regarding the speed of light in a gravitational field. Notice that the correct choice implies that measuring rods are elongated, so that distance measurements are undervalued by the same factor as clock rates are slowed, guaranteeing that local measurements of the speed of light are unaffected by gravity. And of course the presently accepted idea that the true speed of light is reduced in a gravitational field must be rejected.
Appendix II
An integral of motion in a Robertson Walker universe is derived.
The Robertson Walker metric may be written [4: 380]
![]()
depending on whether the curvature of the universe is positive, zero, or negative, respectively. Introducing a new time variable, ![]() , defined7 by
, defined7 by![]() , the metric becomes
, the metric becomes
![]()
In a homogeneous, isotropic universe, one may, without loss of generality, consider the motion to be in the ![]() direction, for which the geodesic equation is
direction, for which the geodesic equation is
![]()
But![]() ,
, ![]() , and
, and![]() . Thus the geodesic equation reduces to
. Thus the geodesic equation reduces to
![]()
Inserting ![]() and integrating, gives
and integrating, gives
![]()
The proper velocity, v, is defined by![]() , where
, where![]() , and
, and![]() .
.
Thus ![]() and the integral may be written,
and the integral may be written,
![]()
But directly from the line element, for the motion considered,
![]()
Inserting this and introducing![]() , the integral of motion may be written
, the integral of motion may be written
![]()
Appendix III
An otherworldly proof of the existence of the aether
Here it is demonstrated that Einstein’s procedure for setting clocks in a multiply connected space (e.g., a flat three-torus) generally produces inconsistent results which can be analyzed to give the velocity of the reference frame relative to the aether.
The special theory of relativity is a local theory: the geometry must be Euclidean, but there is no restriction regarding the topology of the space. The flat three-torus is a locally Euclidean space which may be visualized as the interior of a cubical box in which opposite points on the front & back, top & bottom, and left & right sides are identified as the same point. Of the countable infinity of locally geodesic paths connecting any given pair of points, only four are of interest: first the direct path touching no edge, together with three paths that are the shortest indirect (edge touching) paths connecting the given pair. Laying out the edge-touching geodesic paths connecting two points lying within the cube is simplified by adjoining image boxes, each an identical copy of the original, to form a face-connected crystal. The vector (altogether inside the cube) from the master clock, M, to the slave clock, S, will, in the general case, have a negative dot product with three of the six outward-pointing vectors normal to the six sides of the box. Only indirect geodesic paths beginning at M and directed through one of these three sides to the image of S in an adjoining box need be considered. (The other three sides would result in a path whose length exceeds the edge length.) The indirect paths will be straight lines connecting M to these three images of S.
We now calculate the discrepancies in the proposed settings for one slave clock, S. The analysis applies to any of the four acceptable paths. The calculations will be made in a frame at rest in the aether, with respect to which the frame of the clock system moves with velocity,![]() . A signal will follow the straight path from A to B, with velocity
. A signal will follow the straight path from A to B, with velocity![]() , of magnitude
, of magnitude
![]()
The travel time is
![]()
The time and distance values above are true aether frame values: the proper values are related to the aether values by ![]() and
and![]() . Thus in terms of proper measurements we have
. Thus in terms of proper measurements we have
![]()
For the signal moving from B to A, we just interchange A and B. Since ![]() and,
and, ![]()
![]()
Now consider the setting of the slave clock. According to Einstein’s “definition”, ![]() , so
, so ![]() is presumed to be just half the round-trip time, which has been measured. Thus S is instructed to set his stopped clock
is presumed to be just half the round-trip time, which has been measured. Thus S is instructed to set his stopped clock
to some time, ![]() , and to start the clock when the start signal is received. The start signal is launched from M at time
, and to start the clock when the start signal is received. The start signal is launched from M at time![]() , so as presumably to arrive at S at time
, so as presumably to arrive at S at time![]() . But actually the signal arrives at time
. But actually the signal arrives at time![]() . Now if
. Now if![]() , then
, then ![]() and S will start his clock early, so its setting will be ahead of M’s clock: it will lead by
and S will start his clock early, so its setting will be ahead of M’s clock: it will lead by
![]() .
.
Next we record at S the arrival times the start signals sent along each of the four locally shortest paths connecting M and S. The differences between of the arrival time for indirect paths, S K=1,2,3) and the direct path S0 are
![]()
Let ![]() and
and![]() . The equations to determine
. The equations to determine ![]() may be written as
may be written as
![]()
Or in matrix form, ![]() whence
whence
![]()
Thus Einstein’s procedure for setting a clock in this odd little universe permits the determination of one’s velocity with respect to aether, and hence, a preferred frame of reference at rest in the aether.
It seems unreasonable to imagine that the existence of the aether is a special feature of multiply connected universes, so we may perhaps be confident that the aether pervades our (apparently) simply connected universe. Thus, even though we may not be able to actually determine an aether rest frame, we may be confident of the existence of a preferred frame of reference in which the order in which events occur is well defined, cause preceding effect, in accordance with the realist concept of science.
NOTES
![]()
1Commonly called “General Relativity”, a misnomer. The interpretation offered here argues that only those elements of the matter tensor possessing non-zero rest mass should be included as sources. Otherwise, Einstein’s theory is accepted as is.
2The presentation given here has been simplified as compared with Einstein’s original development.
3Φ < 0 is the gravitational potential.
4This imagined phenomenon is commonly referred to as “gravitational time dilation”.
![]()
5It must be noted that captive radiation, as for instance in the body of a star, exhibits an equivalent rest mass and does interact with, and contribute to, the gravitational field ( [5] , p. 100). Even more striking is the fact that very nearly all of the rest mass of a baryon derives from the kinetic energy of confined massless gluons, and nearly massless quarks: m = E/c2.
![]()
6It is not being suggested that the proper metric should be discarded. The proper metric correctly describes the dynamical behavior of non- zero rest mass matter, which the VRM metric does not describe.
7![]() , where
, where ![]() is the world time and
is the world time and![]() .
.