Employment Protection, Employers’ Hiring Strategies and the Screening Role of Temporary Contracts ()
Received 13 May 2016; accepted 15 July 2016; published 18 July 2016

1. Introduction
One of the most important recent topics in labour economics is the issue of how employment protection legislation affects labour markets. In Europe, high and persistent unemployment rates (compared with those in the US) are thought to result from stringent employment protection that has generated labour market rigidities. In the 1980s, many European countries addressed this problem by liberalising the use of temporary contracts, with the aim of combating unemployment. However, introducing flexible employment contracts into economies with high unemployment produced only inconclusive results and remains theoretically and empirically controversial. Theoretical models predict that more stringent employment protection reduces both job creation and job destruction, which makes the overall effect on employment (and unemployment) ambiguous. This effect may imply that more flexible regulation of temporary employment may create new jobs but that these jobs are not well protected by employment legislation and are therefore unstable. In certain cases, the latter effect dominates the former, and the unemployment rate rises (see [1] and [2] ).
How the policies of easing the use of temporary contracts or relaxing other employment protection legislation affect labour markets depends on employers’ hiring strategies regarding the types of contracts. There are a number of reasons that employers use fixed-term employment contracts. [3] identifies three reasons for their use: 1) saving on future termination costs (and certain fringe benefits); 2) temporary replacement (churning); and 3) screening for permanent positions. If firms are required to pay lower (or no) firing costs with a fixed-term contract when employees are dismissed, hiring a temporary worker will save money. Furthermore, firms might replace incumbent workers with temporary workers and assess the adequacy of these employees for permanent positions. In this regard, temporary replacement enables employee screening. If fixed-term contracts are used to screen employees, then firms can learn about the employee and decide whether the current match should be converted into a permanent form. Although it is controversial whether temporary contracts are stepping stones to permanent contracts or dead-ends, a considerable number of temporary workers are currently being hired into longer-duration contracts in certain European countries (see [4] ).1 The evidence that temporary work can be a stepping stone to permanent work suggests that a screening effect is being exploited by firms with respect to temporary workers. Although a number of studies have incorporated the distinction between contract types into theoretical models that examine the effects of employment protection legislation on labour markets, the screening role of temporary contracts has not been a main focus of research attention. [3] and [7] find indications that temporary contracts help screen workers for permanent positions. Even if a match is revealed to be unproductive, firing a worker from a permanent job is costly in countries with stringent employment protections. The screening role of temporary contracts is thus indispensable in these countries.2 Thus, the purpose of this paper is to theoretically examine how employment protection for permanent jobs affects firms’ hiring decisions and the screening function of temporary contracts when the quality of an employment match (the productivity of a worker-firm pair) is match-specific and not perfectly observable.
The equilibrium search model is helpful in studying the effects of employment protection when both permanent and temporary jobs are considered. In particular, the endogenous job destruction framework constructed by [9] is a standard model for study in this field. In the basic model with endogenous job destruction, the productivity of each job is characterised as a random shock, and the decisions of a firm and a worker depend on the value of productivity. Thus, once a productivity shock occurs, both the firm and the worker can observe it. Under this set-up, conversion of a temporary contract to a permanent one also depends on the realised value of the productivity shock. With respect to the screening role of temporary contracts, such a framework is unsuitable because the productivity of a match is known after the shock, and there is no need to screen workers. In other words, screening is significant for firms when information about worker type or match quality is not fully revealed.3
The present paper has a motivation similar to that of [13] , which extends the model of [14] by introducing permanent and temporary contracts and showing that this type of model can account for the high transition rates from temporary to permanent employment in some European countries.4 [14] originally considered a situation in which only a publicly observable signal regarding the quality of a worker-firm match is obtained at the time of meeting but the true quality of the match is revealed over time after the match has been formed and work has begun.5 [13] adopts this learning mechanism to develop a model in which temporary contracts are used as screening devices.
Although the motivation for this paper is similar to that of [13] , there are two major differences in the structures of the models. First, he assumes that firms can offer temporary employment with exogenous probability, which represents a restriction on the use of temporary contracts. In this paper, however, we consider that firms endogenously choose what type of contract to offer. This enables us to examine how changes in regulations regarding terminating permanent employment contracts distort firms’ optimal hiring decisions. Second, in [13] , a firm is allowed to maintain an employee in a temporary position continuously if the renewal clause is not enforced, which is given by exogenous probability, and even matches with good quality can be retained in a temporary form. In his model, workers may be retained in a temporary position regardless of whether the true match quality is revealed or not. However, we do not permit this possibility, and all temporary jobs can persist for only one period. At the end of each period, only matches in a temporary position with high productivity are converted into permanent contracts. Otherwise, the temporary contracts are terminated. In this regard, we note that the endogenous choice between permanent and temporary jobs is a key element of this model.6 As noted by [22] , the previous literature assumes that temporary jobs are preferable to permanent ones and that all new jobs start as temporary jobs or that regulation forces firms to create permanent jobs. However, various regulations on the use of temporary contracts―pertaining, for example, to valid reasons for using FTCs (fixed-term contracts), the maximum number of successive FTCs and the maximum cumulative duration of successive FTCs―are imposed in many OECD countries. As a result of these regulations, offering temporary contracts may not always be the best choice. Accordingly, we focus on the situation in which a temporary job lasts for only one period7 and show that the types of contracts chosen depend on the realised value of the observed signal of a match type. Because research regarding the choice between temporary and permanent jobs (combined with the screening role of temporary jobs) is limited, our paper offers new insights into the impact of employment protection. Furthermore, because this paper theoretically shows the unique existence of an equilibrium with the endogenous choice of contract type, we are able to qualitatively examine the effect of dismissal costs on hiring standards and the average productivity of permanent jobs and to discuss the effectiveness of the policy of increasing labour market flexibility by weakening firing restrictions for permanent employment.
We further note that the average productivity of permanent jobs is one of the major factors in the analysis of this paper because if temporary contracts are an effective tool for screening workers for permanent positions, employers will expect increased productivity in permanent jobs. Because multiple mechanisms (substitution between general and firm-specific skills, work effort, substitution between permanent and temporary employment, and selection of workers) generally contribute to the effect of employment protection legislation on productivity, it is difficult to address all of these factors in one specific model.8 Among others, [27] draws attention to the match-specific component of productivity and finds that learning about match quality has a more dominant impact on the accumulation of match-specific knowledge than does learning-by-doing. Although the model used in this paper adopts a simpler learning process than that used in [27] , we instead consider the endogenous choice of contract type by employers. This will enable us to achieve new insight into understanding how employment protection for permanent employment affects labour productivity.
One important limitation of our work is that a welfare analysis is not conducted. The major reasons for this are: 1) it is difficult to obtain the analytically clear-cut result regarding how a change in dismissal costs affects the social welfare; and 2) we focus on the employers’ decision on what type of contract to offer. However, whether to increase dismissal costs or to decrease them should be determined from the viewpoint of social efficiency. In this regard, a detailed numerical analysis is required.
The remainder of the paper is organised as follows. In Section 2, the basic framework of the model is described. In Section 3, a steady-state equilibrium is characterised. In Section 4, we investigate how dismissal costs affect job creation and the hiring thresholds for each type of contract. Finally, Section 5 concludes.
2. Model
2.1. Description of the Economy
We extend the model studied by [14] to allow for two types of employment contracts: temporary and permanent. We employ a discrete-time framework and assume that both workers and firms discount the future by a constant rate  (which is a discount factor). Many workers are either employed or unemployed, and the measure of workers is normalised to one. On-the-job searches are ruled out, and thus only unemployed workers search for jobs. Firms are measured by the free entry/exit condition. All workers and firms are assumed to be risk-neutral.
(which is a discount factor). Many workers are either employed or unemployed, and the measure of workers is normalised to one. On-the-job searches are ruled out, and thus only unemployed workers search for jobs. Firms are measured by the free entry/exit condition. All workers and firms are assumed to be risk-neutral.
This model explicitly includes labour market friction; therefore, job seeking and recruiting activities are time consuming. We assume that the meeting process is described by constant-returns-to-scale matching technology, 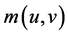 , where u and v are measures of unemployed workers and vacancies, respectively. During each period, a firm with a vacancy encounters a job seeker with probability
, where u and v are measures of unemployed workers and vacancies, respectively. During each period, a firm with a vacancy encounters a job seeker with probability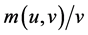 , and an unemployed worker encounters a vacancy with probability
, and an unemployed worker encounters a vacancy with probability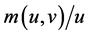 . Let the former probability be denoted by
. Let the former probability be denoted by  and the latter probability denoted by
and the latter probability denoted by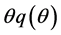 , where
, where  denotes labour market tightness. By assuming the constant-returns- to-scale matching technology, these probabilities can be represented as functions of only market tightness,
denotes labour market tightness. By assuming the constant-returns- to-scale matching technology, these probabilities can be represented as functions of only market tightness,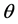 . We assume that
. We assume that 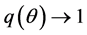 and
and 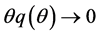 as
as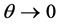 , and that
, and that  and
and 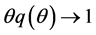 as
as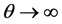 .
.
The production technology and the learning processes regarding match quality are based on [13] and [14] . We first consider the production technology; a unit of production is a matched worker-firm pair, and the productivity of each job is match-specific.9 As in the above literature, match-specific productivity is observed at the end of the period; it is represented by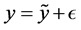 , where
, where ![]() is a zero-mean, independently and identically distributed, random variable and follows a uniform distribution with support
is a zero-mean, independently and identically distributed, random variable and follows a uniform distribution with support![]() .
. ![]() is the true quality of a match, which is either high or low; matches with high productivity are represented by
is the true quality of a match, which is either high or low; matches with high productivity are represented by![]() , and matches with low productivity are represented by
, and matches with low productivity are represented by![]() . Owing to the presence of the noise term
. Owing to the presence of the noise term![]() , neither the worker nor the firm can observe the true productivity of the match.
, neither the worker nor the firm can observe the true productivity of the match.
Match quality is considered to be both an inspection and an experience good. When a job seeker and a vacant firm meet, they observe a signal![]() , which represents the probability that the match will be good. This signal is drawn from the cumulative distribution
, which represents the probability that the match will be good. This signal is drawn from the cumulative distribution ![]() and is independent across matches. We assume that firms make hiring decisions based only on the realisation of
and is independent across matches. We assume that firms make hiring decisions based only on the realisation of![]() . After forming a match, a worker and a firm observe productivity (y) and update their information about the true match quality. If realised productivity falls in the range
. After forming a match, a worker and a firm observe productivity (y) and update their information about the true match quality. If realised productivity falls in the range![]() , the worker and firm learn that the match has high productivity. Similarly, if realised productivity falls in the range
, the worker and firm learn that the match has high productivity. Similarly, if realised productivity falls in the range![]() , the match is revealed to be of low quality. If realised productivity is in the range
, the match is revealed to be of low quality. If realised productivity is in the range![]() , nothing is learned (we assume that
, nothing is learned (we assume that![]() ). Thus, the learning process is a form of “all-or-nothing”. Let
). Thus, the learning process is a form of “all-or-nothing”. Let ![]() denote the probability that the true match quality is revealed. In this setting, a match of an unknown type with prior probability
denote the probability that the true match quality is revealed. In this setting, a match of an unknown type with prior probability ![]() will be revealed as high productivity with probability
will be revealed as high productivity with probability ![]() and will be revealed as low productivity with probability
and will be revealed as low productivity with probability![]() .
.
2.2. Contracts
In this model, two types of contracts are considered: temporary and permanent. In addition, there are two states of permanent contracts: pre-existing and newly created. When pre-existing permanent workers are dismissed, firms must pay fixed dismissal costs (firing taxes)![]() . However, no cost is imposed when new permanent workers and temporary workers are dismissed. The transfer component of dismissal costs is not considered in this paper.10
. However, no cost is imposed when new permanent workers and temporary workers are dismissed. The transfer component of dismissal costs is not considered in this paper.10
Separations from permanent jobs occur (i) when the match quality is revealed to be bad or (ii) when each firm experiences the negative shock with constant probability![]() . With respect to temporary jobs, however, we further assume that employees are dismissed if the true quality of the match is not revealed. In this regard, we implicitly assume that the maximum length of temporary contracts is legally limited and that a firm with a temporary job neither rehires its employee through a permanent contract in the next period. More details regarding this point are provided in the next subsection. When the use of temporary contracts is rather restrictive in this way, offering a permanent contract when opening a vacancy is a better choice for employers within certain range of a signal. We will show in a later section that there exists a unique cut-off value of
. With respect to temporary jobs, however, we further assume that employees are dismissed if the true quality of the match is not revealed. In this regard, we implicitly assume that the maximum length of temporary contracts is legally limited and that a firm with a temporary job neither rehires its employee through a permanent contract in the next period. More details regarding this point are provided in the next subsection. When the use of temporary contracts is rather restrictive in this way, offering a permanent contract when opening a vacancy is a better choice for employers within certain range of a signal. We will show in a later section that there exists a unique cut-off value of ![]() that is determined by the equivalence between offering permanent versus temporary contracts. This contrasts with the situation in which firms always prefer offering temporary contracts, as assumed in [13] and other related literature that is based on a model of endogenous job destruction.
that is determined by the equivalence between offering permanent versus temporary contracts. This contrasts with the situation in which firms always prefer offering temporary contracts, as assumed in [13] and other related literature that is based on a model of endogenous job destruction.
2.3. Bellman Equations
To derive the values of firms with each type of contract, some notation must be defined. Let us denote the value of a firm with a temporary job and a signal ![]() by
by ![]() and the value of a firm with a permanent job and a signal
and the value of a firm with a permanent job and a signal ![]() by
by![]() , where I is an indicator function that takes zero for a new permanent match and one for a pre-existing match. The value of a vacant job is denoted by V.
, where I is an indicator function that takes zero for a new permanent match and one for a pre-existing match. The value of a vacant job is denoted by V.
The expected value of a firm that has a temporary job and a signal ![]() is represented by
is represented by
![]() (1)
(1)
where ![]() is the wage paid for a temporary job. As defined above,
is the wage paid for a temporary job. As defined above, ![]() is the probability that a match will be good, and flow productivity is given by the expected value, using
is the probability that a match will be good, and flow productivity is given by the expected value, using![]() . At the end of the period, a match-specific shock is realised, with the employer learning that the true quality of a match is high with probability
. At the end of the period, a match-specific shock is realised, with the employer learning that the true quality of a match is high with probability ![]() and low with probability
and low with probability![]() . With probability
. With probability![]() , the quality of a match is not revealed. In this case, the prediction regarding the quality of a match cannot be revised, and the employment relationship is terminated because temporary contracts cannot be renewed in the next period. We note that instead of this strong assumption, the model can be extended to allow for continuing temporary contacts in the next period. Let us denote the retention probability by
, the quality of a match is not revealed. In this case, the prediction regarding the quality of a match cannot be revised, and the employment relationship is terminated because temporary contracts cannot be renewed in the next period. We note that instead of this strong assumption, the model can be extended to allow for continuing temporary contacts in the next period. Let us denote the retention probability by ![]() (s is the probability that the current employment relationship under a temporary contract terminates); Equation (1) is rewritten as follows:
(s is the probability that the current employment relationship under a temporary contract terminates); Equation (1) is rewritten as follows:
![]() (1’)
(1’)
Then, Equation (1) is a special case of (1’) when![]() . For a large s, we can show the unique existence of
. For a large s, we can show the unique existence of![]() , which makes employers indifferent towards temporary versus permanent jobs. Furthermore, the main results of this paper would not be essentially affected under this generalised situation. As mentioned in [30] , the transition rates from temporary employment to regular employment as of both one year and three years after the reference period are much lower in Japan than in many European countries. Particularly in Japan, the employment status of temporary workers is likely to be unchanged as of one year after the reference period, which means that they will be hired as temporary employment within the same firm. The term
, which makes employers indifferent towards temporary versus permanent jobs. Furthermore, the main results of this paper would not be essentially affected under this generalised situation. As mentioned in [30] , the transition rates from temporary employment to regular employment as of both one year and three years after the reference period are much lower in Japan than in many European countries. Particularly in Japan, the employment status of temporary workers is likely to be unchanged as of one year after the reference period, which means that they will be hired as temporary employment within the same firm. The term ![]() in the second line of (1’) captures this observation. Therefore, although this paper focuses on the simplest case
in the second line of (1’) captures this observation. Therefore, although this paper focuses on the simplest case![]() , we substantially consider a situation in which a temporary match with unknown productivity can be retained in the next period with some probability.11 For comparison, if the last term
, we substantially consider a situation in which a temporary match with unknown productivity can be retained in the next period with some probability.11 For comparison, if the last term ![]() in (1) were replaced by
in (1) were replaced by![]() , employers always prefer temporary employment to permanent employment.
, employers always prefer temporary employment to permanent employment.
The expected value of a firm with a permanent job and signal ![]() is represented by
is represented by
![]() (2)
(2)
where ![]() is the wage paid for a permanent job of type I
is the wage paid for a permanent job of type I![]() . Newly created matches are not covered by employment protection, and the outside option of these matches thus does not include dismissal costs. Conversely, all matches are covered by employment protection one period later, and employers must pay dismissal costs for firing workers. The final term in (2) represents the situation in which the separation of matches of unknown quality depends on the realised value of
. Newly created matches are not covered by employment protection, and the outside option of these matches thus does not include dismissal costs. Conversely, all matches are covered by employment protection one period later, and employers must pay dismissal costs for firing workers. The final term in (2) represents the situation in which the separation of matches of unknown quality depends on the realised value of![]() . In the steady-state equilibrium, however, all matches of unknown quality are retained in the form of permanent contracts because, as we will show in a later section,
. In the steady-state equilibrium, however, all matches of unknown quality are retained in the form of permanent contracts because, as we will show in a later section, ![]() is strictly greater than zero. We suppose that the quality of a match is unchanged when the match is retained.
is strictly greater than zero. We suppose that the quality of a match is unchanged when the match is retained.
The expected value of a vacant firm is represented by
![]() (3)
(3)
where c denotes the flow recruiting costs and ![]()
![]() is the hiring threshold for contract type j (P represents “permanent”, and T represents “temporary”). We here assume that
is the hiring threshold for contract type j (P represents “permanent”, and T represents “temporary”). We here assume that![]() , as formally shown below. In Equation (3), the employers’ choice regarding whether an employment match is designated as permanent or temporary depends on the realisation of the signal
, as formally shown below. In Equation (3), the employers’ choice regarding whether an employment match is designated as permanent or temporary depends on the realisation of the signal![]() .
.
Let us denote the value of being employed in a temporary job with signal ![]() as
as![]() . The value of being employed in a permanent job with signal
. The value of being employed in a permanent job with signal ![]() and the value of being unemployed are denoted by
and the value of being unemployed are denoted by ![]() and U, respectively (I is the indicator function that was defined above). The expected value of being employed in a temporary job with signal
and U, respectively (I is the indicator function that was defined above). The expected value of being employed in a temporary job with signal ![]() is represented by
is represented by
![]() (4)
(4)
where ![]() represents the constant disutility of work.
represents the constant disutility of work.
The expected value of being employed in a permanent job with signal ![]() is represented by
is represented by
![]() (5)
(5)
and the expected value of being unemployed is represented as follows:
![]() (6)
(6)
2.4. Surplus of a Match
Let us define the joint surplus generated from forming a match as follows:
![]()
![]()
where each equation is evaluated at any![]() . The first equation represents the surplus of a permanent job with current status I. The second equation represents the surplus of a temporary job. The type of match formed depends on the level of the observed signal
. The first equation represents the surplus of a permanent job with current status I. The second equation represents the surplus of a temporary job. The type of match formed depends on the level of the observed signal![]() . We suppose that the wage for each job is determined by a standard asymmetric Nash bargaining process, and we denote the worker’s bargaining power by
. We suppose that the wage for each job is determined by a standard asymmetric Nash bargaining process, and we denote the worker’s bargaining power by![]() . Under this wage determination mechanism, the worker and the firm that form a match divide the surplus according to the following sharing rule:
. Under this wage determination mechanism, the worker and the firm that form a match divide the surplus according to the following sharing rule:
![]() (7)
(7)
![]() (8)
(8)
Using these sharing rules, we derive the expressions for joint surplus as follows. First, the joint surplus values for permanent jobs are given by
![]() (9)
(9)
![]() (10)
(10)
where we use the free-entry condition that the values of vacancies in each state are equal to zero:![]() . Second, the surplus
. Second, the surplus ![]() generated by forming a temporary match is represented by
generated by forming a temporary match is represented by
![]() (11)
(11)
3. Equilibrium
3.1. Hiring Decision
We first consider the hiring decisions of firms with permanent jobs. Because firms can choose a form of contract with no cost, a firm decides to hire a worker on a permanent basis if offering a permanent contract is more profitable than offering a temporary contract. The corresponding condition for determining the optimal hiring standard is given by![]() . To obtain a concrete expression for this condition, it is useful to express
. To obtain a concrete expression for this condition, it is useful to express ![]() in a more tractable form. From (10), we obtain
in a more tractable form. From (10), we obtain
![]() (12)
(12)
Utilising (9), (10) and (12), the following two results are derived:
![]() (13)
(13)
![]() (14)
(14)
The first result depicts the relationship between ![]() and
and![]() . The surplus generated by a pre-existing permanent job is equal to the sum of the surplus generated by a newly created permanent job and the cost of dismissal. The second result indicates that
. The surplus generated by a pre-existing permanent job is equal to the sum of the surplus generated by a newly created permanent job and the cost of dismissal. The second result indicates that ![]() is independent of
is independent of![]() , where
, where ![]() represents the differentiation of
represents the differentiation of ![]() with respect to
with respect to![]() . After a match is revealed to be good
. After a match is revealed to be good![]() , the surplus in this case is expressed by
, the surplus in this case is expressed by
![]() (15)
(15)
![]()
This automatically holds under the assumption provided in Proposition 1.
We assume that ![]() is sufficiently high that the numerator of (15) is positive, which would indicate that (14) has a positive sign and that
is sufficiently high that the numerator of (15) is positive, which would indicate that (14) has a positive sign and that ![]() is increasing in
is increasing in![]() .12
.12
We next consider the existence of ![]() that satisfies
that satisfies![]() . It follows from (9) and (11) that
. It follows from (9) and (11) that
![]() (16)
(16)
and the condition ![]() is expressed as
is expressed as
![]() (17)
(17)
This results in
![]() (17’)
(17’)
Subsequently, (11) yields the explicit form of![]() , which is characterised by
, which is characterised by![]() :
:
![]() (18)
(18)
Because ![]() must be greater than zero, we suppose that the realisation of
must be greater than zero, we suppose that the realisation of ![]() is unprofitable and that the following condition is satisfied for a given
is unprofitable and that the following condition is satisfied for a given![]() :
:
![]() (19)
(19)
This condition requires that ![]() be sufficiently low for any positive
be sufficiently low for any positive![]() .13 Otherwise, even if the true productivity is
.13 Otherwise, even if the true productivity is ![]() with probability one, the expected costs of recruiting job seekers are lower than the expected net productivity
with probability one, the expected costs of recruiting job seekers are lower than the expected net productivity![]() , and every worker-firm pair yields non-negative profits, regardless of the realisation of
, and every worker-firm pair yields non-negative profits, regardless of the realisation of![]() . We do not consider this case.
. We do not consider this case.
For the value of a ![]() that is a solution to Equation (17), the following proposition is obtained.
that is a solution to Equation (17), the following proposition is obtained.
Proposition 1. There exists a unique ![]() that satisfies (17) and is contained in the interval
that satisfies (17) and is contained in the interval ![]() if (19) holds and
if (19) holds and ![]() is sufficiently high to satisfy the following condition for a given
is sufficiently high to satisfy the following condition for a given![]() :
:
![]() (20)
(20)
Furthermore, ![]() is strictly greater than
is strictly greater than![]() .
.
Proof. See Appendix A.
Condition (20) is required for the presence of![]() , which is contained in the interval
, which is contained in the interval![]() . Similar to (19), condition (20) will be satisfied under a reasonable value of d. We here note that there are countries in which the hiring threshold for permanent jobs is quite high and most newly created jobs are temporary.14 This case is obtained for a sufficiently large d. In this case,
. Similar to (19), condition (20) will be satisfied under a reasonable value of d. We here note that there are countries in which the hiring threshold for permanent jobs is quite high and most newly created jobs are temporary.14 This case is obtained for a sufficiently large d. In this case, ![]() becomes close to one, and it is optimal for most firms with vacancies to offer temporary contracts.
becomes close to one, and it is optimal for most firms with vacancies to offer temporary contracts.
The determination of hiring thresholds is described in Figure 1. ![]() is given by an intersection of the horizontal axis and
is given by an intersection of the horizontal axis and![]() , and
, and ![]() is given by an intersection of
is given by an intersection of ![]() and
and![]() . As shown in Figure 1, employers set a higher hiring threshold for permanent contracts relative to temporary contracts. The crucial difference between the two is whether dismissal costs are imposed. If
. As shown in Figure 1, employers set a higher hiring threshold for permanent contracts relative to temporary contracts. The crucial difference between the two is whether dismissal costs are imposed. If ![]() takes a low value, a contract is more likely to be terminated. In a permanent contract, an employer must pay these termination costs, and a lower
takes a low value, a contract is more likely to be terminated. In a permanent contract, an employer must pay these termination costs, and a lower ![]() increases the probability of this event. Therefore, a high probability of a good match is necessary for a permanent contract to compensate for the higher expected costs. We further note that employers’ choice between permanent and temporary contracts is endogenous and that a unique value of
increases the probability of this event. Therefore, a high probability of a good match is necessary for a permanent contract to compensate for the higher expected costs. We further note that employers’ choice between permanent and temporary contracts is endogenous and that a unique value of ![]() exists. Given the assumption that temporary jobs last one period, a portion of newly created jobs take the form of permanent contracts
exists. Given the assumption that temporary jobs last one period, a portion of newly created jobs take the form of permanent contracts![]() .
.
We further note that ![]() for
for![]() . This implies that
. This implies that ![]() and
and ![]() for any
for any ![]() that is greater than
that is greater than![]() . Therefore, employers prefer retaining a permanent worker to dismissing him (or her), even when the true quality of the match is not revealed, because the probability that the quality of a match is good remains high in permanent jobs.
. Therefore, employers prefer retaining a permanent worker to dismissing him (or her), even when the true quality of the match is not revealed, because the probability that the quality of a match is good remains high in permanent jobs.
3.2. Job Creation
The measure of vacant jobs that is posted in equilibrium is determined by the free-entry condition. Equation (4),
with![]() , implies
, implies
![]() (21)
(21)
where
![]()
The LHS of (21) increases in ![]() because
because ![]() is a decreasing function of
is a decreasing function of![]() . The impact of
. The impact of ![]() on the RHS of (21) is more complicated, but we are able to show that it decreases in
on the RHS of (21) is more complicated, but we are able to show that it decreases in![]() . Differentiating the RHS of (21) with respect to
. Differentiating the RHS of (21) with respect to ![]() yields
yields
![]()
From (15), ![]() decreases in
decreases in![]() , and the following results hold:
, and the following results hold:
![]()
Regarding the first two results, increased market tightness reduces the meeting probability of employers; therefore, employers raise their hiring thresholds to ensure profits. Taking from (16) that ![]() for any
for any![]() , we conclude that the RHS of (21) decreases with
, we conclude that the RHS of (21) decreases with![]() . The conclusion of this subsection can thus be summarised as follows:
. The conclusion of this subsection can thus be summarised as follows:
Proposition 2. There exists a unique value of ![]() that satisfies the job creation condition (21).15
that satisfies the job creation condition (21).15
As observed by [17] , it is difficult to show analytically the unique existence of a steady-state equilibrium in a Pries-Rogerson type model in which permanent and temporary jobs are incorporated. However, our model overcomes this difficulty and enables us to investigate the impact of employment protection analytically.
3.3. Employment Flows
Let us denote the steady-state measure of permanent workers by ![]() and the measure of temporary workers by
and the measure of temporary workers by![]() . Similarly, the measure of matches that are known to be good is denoted by
. Similarly, the measure of matches that are known to be good is denoted by![]() , and the measure of matches of unknown quality is denoted by
, and the measure of matches of unknown quality is denoted by![]() . In the steady-state equilibrium, the following equivalence conditions must hold in each employment pool.
. In the steady-state equilibrium, the following equivalence conditions must hold in each employment pool.
The equivalence of the inflow and outflow from the employment pool of temporary contracts yields the following condition:
![]() (22)
(22)
The LHS of (22) reflects the assumption that every temporary contract is terminated in the next period and that each temporary worker will be either employed with a permanent contract or unemployed. Regarding the RHS of (22), only worker-firm pairs that realise a signal contained in ![]() form temporary contract matches.
form temporary contract matches.
In the pool of high-quality employment, the equivalence of the inflows and outflows yields
![]() (23)
(23)
where
![]() (24)
(24)
![]() (25)
(25)
The LHS of (23) indicates that a negative shock, which occurs with probability![]() , causes the separation of the employment relationship. The RHS of (23) indicates that matches for both temporary and permanent positions of unknown type are revealed to show high productivity with probability
, causes the separation of the employment relationship. The RHS of (23) indicates that matches for both temporary and permanent positions of unknown type are revealed to show high productivity with probability ![]() multiplied by the expected value of the signal (
multiplied by the expected value of the signal (![]() represents the probability that an unknown match with a signal
represents the probability that an unknown match with a signal ![]() is found to be good).
is found to be good).
In the employment pool of permanent jobs with unknown productivity, the following equivalence condition is obtained:
![]() (26)
(26)
In the LHS of (26), outflows from this employment pool result from negative economic shocks and the revelation of matches that are either low or high productivity. The RHS of (26) captures inflows into this pool; it is composed of newly formed matches with signals that exceed![]() . Note that
. Note that ![]() represents the measure of matches of unknown productivity in permanent contracts. Figure 2 represents the employment flows that are described in this subsection.
represents the measure of matches of unknown productivity in permanent contracts. Figure 2 represents the employment flows that are described in this subsection.
Together with two additional conditions,
![]() (27)
(27)
![]() (28)
(28)
(22), (23) and (26)-(28) determine the steady-state value of ![]() and u. Solving these equations, we obtain
and u. Solving these equations, we obtain
![]() (29)
(29)
![]() (30)
(30)
![]()
Figure 2. Employment ows (![]() is the measure of permanent workers with unknown match productivity).
is the measure of permanent workers with unknown match productivity).
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
where
![]()
3.4. Wages
Because the surplus sharing rules have already been derived, we are able to solve the Nash wage equations for each type of employment contract. From (4) and (8), the wage equations for temporary contracts are given by
![]() (34)
(34)
Similarly, it follows from (5) and (7) that the wage equations for permanent contracts of type I are given by
![]() (35)
(35)
![]() (36)
(36)
Note that wages do not play a crucial role in the characterisation of the steady-state equilibrium because wages in both types of jobs are determined by the standard Nash bargaining problem and it is sufficient to focus on the surplus sharing rules given by (7) and (8).
The steady-state equilibrium in this model is characterised by ![]() , which are determined by (17’), (18), (21), (19)-(36). Because
, which are determined by (17’), (18), (21), (19)-(36). Because ![]() and
and ![]() are uniquely determined, other endogenous variables are also uniquely determined.
are uniquely determined, other endogenous variables are also uniquely determined.
4. The Effect of Dismissal Costs on Major Endogenous Variables
4.1. The Effect of Dismissal Costs on Job Creation and Hiring Thresholds
To examine the effects of dismissal costs on firms’ hiring decisions in a steady-state equilibrium, we first consider how these costs affect labour market tightness. For that purpose, the effects of d on the hiring thresholds must be identified. It follows from (15) and (18) that for a given![]() , a response of
, a response of ![]() to a change in d is given by
to a change in d is given by
![]() (37)
(37)
where ![]() stands for
stands for![]() . Higher dismissal costs increase the hiring threshold for temporary jobs because an increase in the future expected surplus is offset by the increased dismissal cost (
. Higher dismissal costs increase the hiring threshold for temporary jobs because an increase in the future expected surplus is offset by the increased dismissal cost (![]() decreases with higher dismissal costs).
decreases with higher dismissal costs).
From (17’), a change in d has the following effect on ![]() for a given
for a given![]() :
:
![]() (38)
(38)
where
![]()
Although (38) is somewhat complex, we are able to identify its sign explicitly. The result is summarised in the following Lemma.
Lemma 1. An increase in dismissal costs raises ![]() for a given
for a given ![]() if (20) is satisfied.
if (20) is satisfied.
Proof. See Appendix B.
We provide the same interpretation as in the case of![]() . Using the results regarding the hiring thresholds described above, the effect of an increased dismissal cost on job creation is examined. The effect of an increase in d on the RHS of (21) for a given
. Using the results regarding the hiring thresholds described above, the effect of an increased dismissal cost on job creation is examined. The effect of an increase in d on the RHS of (21) for a given ![]() is given as follows:
is given as follows:
![]() (39)
(39)
From (37) and Lemma 1, we obtain the following proposition regarding the effect of dismissal costs on job creation.
Proposition 3. The sign of (39) is negative and ![]() if
if ![]() is sufficiently high.
is sufficiently high.
Proof. See Appendix C.
For a higher![]() , a change in d has a minimal impact on
, a change in d has a minimal impact on ![]() (it tends to zero as
(it tends to zero as ![]() goes to one). Then, the positive impact of d on the expected profits from having a permanent job is negligible. Higher dismissal costs raise the hiring threshold for each type of employment contract for a given labour market tightness, and firms with vacancies thus take a longer time to form matches. This outcome decreases the expected profit from vacancies and job creation.
goes to one). Then, the positive impact of d on the expected profits from having a permanent job is negligible. Higher dismissal costs raise the hiring threshold for each type of employment contract for a given labour market tightness, and firms with vacancies thus take a longer time to form matches. This outcome decreases the expected profit from vacancies and job creation.
The result obtained in Proposition 3 may be standard and intuitive. However, the main focus of this paper lies in how the costs of firing employees affect employers’ hiring policies. At first glance, it appears to be difficult to obtain clear-cut results regarding the effect of dismissal costs on hiring thresholds, ![]() and
and![]() . The reason for this finding is that increasing d has a negative indirect effect on
. The reason for this finding is that increasing d has a negative indirect effect on ![]() and
and ![]() through changing the labour market tightness, whereas increasing d has a positive direct effect on
through changing the labour market tightness, whereas increasing d has a positive direct effect on ![]() and
and![]() , as (37) and Lemma 1 show. However, we are able to find conditions under which signs of
, as (37) and Lemma 1 show. However, we are able to find conditions under which signs of ![]() and
and ![]() are identified. Regarding
are identified. Regarding![]() , we then obtain the following proposition.
, we then obtain the following proposition.
Proposition 4. Suppose that ![]() is sufficiently high to satisfy the following conditions:
is sufficiently high to satisfy the following conditions:
![]() (40)
(40)
![]() (41)
(41)
Then, increasing dismissal costs for permanent jobs raises the hiring threshold ![]() if z is sufficiently high to satisfy the following conditions:
if z is sufficiently high to satisfy the following conditions:
![]() (42)
(42)
![]() (43)
(43)
Proof. See Appendix D.
We will provide a graphical explanation of Proposition 4 based on Figure 3. The left side of Figure 3 depicts how the equilibrium value of ![]() responds to an increase in d. Recalling that
responds to an increase in d. Recalling that ![]() is determined at the intersection of
is determined at the intersection of ![]() and
and![]() , which are linear functions of
, which are linear functions of![]() , we focus changes in the slope and intercept of each surplus. It follows from (11) and (15) that higher dismissal costs make the slope of
, we focus changes in the slope and intercept of each surplus. It follows from (11) and (15) that higher dismissal costs make the slope of ![]() steeper and increase the intercept of
steeper and increase the intercept of![]() . In contrast, the impacts of d on the slope of
. In contrast, the impacts of d on the slope of ![]() and the intercept of
and the intercept of ![]() are indeterminate because it follows from (12), (13), (15) and the result
are indeterminate because it follows from (12), (13), (15) and the result ![]() that we obtain
that we obtain
![]()
![]()
The signs of these equations depend on the magnitude of![]() . When z is sufficiently high and
. When z is sufficiently high and ![]() is low, however, a change in the slope of
is low, however, a change in the slope of ![]() has limited impact on the determination of
has limited impact on the determination of![]() . Therefore, we should concentrate on the intercept of
. Therefore, we should concentrate on the intercept of![]() . A lower value of
. A lower value of ![]() indicates that the true match quality is not likely to be revealed. Because permanent contracts are assumed to be retained even if the true match quality is unknown at the end of each period, employers are able to save future dismissal costs. This effect mitigates the reduction of expected profits caused by increased dismissal costs and decreases the magnitude of
indicates that the true match quality is not likely to be revealed. Because permanent contracts are assumed to be retained even if the true match quality is unknown at the end of each period, employers are able to save future dismissal costs. This effect mitigates the reduction of expected profits caused by increased dismissal costs and decreases the magnitude of ![]() (a higher
(a higher ![]() will have the similar effect). Then,
will have the similar effect). Then, ![]() is likely to decrease, which leads to an increase in
is likely to decrease, which leads to an increase in ![]() (
(![]() goes to
goes to ![]() as demonstrated in Figure 3). Therefore, when a match’s productivity is more dispersed and it is difficult to expose the true quality of the match through on-the-job screening, increased dismissal costs raise the hiring threshold for permanent jobs.
as demonstrated in Figure 3). Therefore, when a match’s productivity is more dispersed and it is difficult to expose the true quality of the match through on-the-job screening, increased dismissal costs raise the hiring threshold for permanent jobs.
Remembering that Proposition 3 is likely to hold under a higher value of![]() , we suppose that
, we suppose that ![]() for simplicity in the following analysis. Regarding the effect of d on
for simplicity in the following analysis. Regarding the effect of d on![]() , then we obtain the following proposition.
, then we obtain the following proposition.
Proposition 5. Increasing dismissal costs for permanent jobs decreases ![]() if (i) z is sufficiently high (
if (i) z is sufficiently high (![]() is low) such that at least the following condition holds:
is low) such that at least the following condition holds:
![]() (44)
(44)
![]()
Figure 3. (Left) The effect of d on![]() ; (Right) The effect of d on
; (Right) The effect of d on![]() .
.
and (ii) the expected costs of a vacancy are less affected by a change in![]() .
.
Proof. See Appendix E.
Although the effect of d on the slope of ![]() is ambiguous, this has a lesser impact on
is ambiguous, this has a lesser impact on ![]() for a lower
for a lower![]() , and an increase in the intercept of
, and an increase in the intercept of ![]() dominantly lowers the hiring threshold for temporary jobs. Therefore, the overall effect of increasing d on
dominantly lowers the hiring threshold for temporary jobs. Therefore, the overall effect of increasing d on ![]() is likely to be negative under the condition (44) (
is likely to be negative under the condition (44) (![]() goes to
goes to![]() , as demonstrated in Figure 3).
, as demonstrated in Figure 3).
It is worth noting that changes in dismissal costs have different impacts on hiring thresholds between permanent and temporary contracts under similar conditions on z (match productivity is more dispersed). As noted in (37) and Lemma 1, a direct impact of d on each hiring threshold is positive for a given![]() . Furthermore, because
. Furthermore, because ![]() and
and ![]() for
for![]() , the indirect impact of d on these thresholds through
, the indirect impact of d on these thresholds through ![]() is negative. However, Proposition 4 states that the total impact of d on
is negative. However, Proposition 4 states that the total impact of d on ![]() is positive for a lower value of
is positive for a lower value of ![]() (a higher value of z), whereas Proposition 5 states that the total impact of d on
(a higher value of z), whereas Proposition 5 states that the total impact of d on ![]() is negative under the similar condition. We will consider the reason for the difference in the reaction to a change in d between
is negative under the similar condition. We will consider the reason for the difference in the reaction to a change in d between ![]() and
and![]() .16
.16
First, we focus on the hiring threshold for temporary contracts. For a given ![]() and any
and any![]() , it follows from (11) that an increase in d decreases
, it follows from (11) that an increase in d decreases ![]() through
through![]() , but its impact lessens as
, but its impact lessens as ![]() decreases. Then, the upward pressure of d on
decreases. Then, the upward pressure of d on ![]() is mitigated. We further note that a change in
is mitigated. We further note that a change in ![]() has a larger impact on
has a larger impact on ![]() under a lower value of
under a lower value of![]() . A higher
. A higher ![]() decreases the probability of finding a job seeker for firms with vacancies
decreases the probability of finding a job seeker for firms with vacancies![]() . Because only temporary contract matches in which the true quality is revealed to be good are converted to permanent contracts, a lower
. Because only temporary contract matches in which the true quality is revealed to be good are converted to permanent contracts, a lower![]() , which means a decrease in the probability that the true quality is revealed, increases the separation probability of temporary jobs, and firms suffer longer recruitment durations. Then, a lower
, which means a decrease in the probability that the true quality is revealed, increases the separation probability of temporary jobs, and firms suffer longer recruitment durations. Then, a lower ![]() amplifies the impact of
amplifies the impact of ![]() on
on![]() , and the negative indirect effect of dismissal costs on
, and the negative indirect effect of dismissal costs on ![]() exceeds its positive direct effect. Thus, the hiring threshold for temporary contracts is reduced.
exceeds its positive direct effect. Thus, the hiring threshold for temporary contracts is reduced.
Second, regarding the hiring threshold for permanent contracts, note that ![]() satisfies
satisfies![]() . As explained in the previous paragraph, the direct impact of d on
. As explained in the previous paragraph, the direct impact of d on ![]() is mitigated under a lower
is mitigated under a lower![]() . From (12), (13) and (14), the impact of d on
. From (12), (13) and (14), the impact of d on![]() , which shifts
, which shifts ![]() downward for a given
downward for a given![]() , is not affected by the value of
, is not affected by the value of ![]() if
if ![]() is close to one. The impact of a downward shift of
is close to one. The impact of a downward shift of ![]() is likely to be greater than the impact of a shift of
is likely to be greater than the impact of a shift of![]() . Regarding the impact of
. Regarding the impact of ![]() on
on![]() , a significant point to be emphasised is that a lower
, a significant point to be emphasised is that a lower ![]() decreases the separation probability of matches associated with permanent contracts because a permanent job does not separate until its true type is revealed to be bad. Although a higher
decreases the separation probability of matches associated with permanent contracts because a permanent job does not separate until its true type is revealed to be bad. Although a higher ![]() decreases the success rate of recruiting, employers can avoid suffering this adverse effect when
decreases the success rate of recruiting, employers can avoid suffering this adverse effect when ![]() has a lower value. Then, the lower
has a lower value. Then, the lower ![]() contributes to a positive sign of
contributes to a positive sign of![]() . In total, the difference between
. In total, the difference between ![]() and
and ![]() in the hiring threshold reaction to a change in dismissal costs reflects the difference in how
in the hiring threshold reaction to a change in dismissal costs reflects the difference in how ![]() (or z) affects both the direct and the indirect effects of d on each hiring threshold.
(or z) affects both the direct and the indirect effects of d on each hiring threshold.
4.2. The Effect of Dismissal Costs on Labour Productivity
Because this paper focuses on the screening role of temporary contracts, we have an interest in the impact of dismissal costs on the screening function of temporary contracts from the viewpoint of firms. In this regard, the average productivity of permanent jobs will be appropriate. If temporary contracts are effectively used as screening devices and potentially unproductive matches are eliminated, employers will expect an increase in the productivity of permanent jobs. Using the results regarding the effect of d on ![]() and
and![]() , we examine how changing dismissal costs affects the average productivity of permanent jobs.
, we examine how changing dismissal costs affects the average productivity of permanent jobs.
We first define the average productivity of permanent jobs as follows:
![]()
where ![]() is defined as
is defined as
![]()
There are two types of permanent jobs: (i) the true match quality is good; (ii) the true match quality is not revealed. Note that the productivity of the latter type is expressed using![]() . We then obtain the following proposition.
. We then obtain the following proposition.
Proposition 6. Suppose that the results of Proposition 4 and Proposition 5 hold. Then, increasing firing costs for permanent jobs increases their average productivity.
Proof. See Appendix F.
This proposition shows that higher dismissal costs improve the average productivity of permanent jobs because of (i) the increased proportion of good-quality jobs among permanent jobs ![]() and (ii) a rise in the conditional expectation of inspection probability (
and (ii) a rise in the conditional expectation of inspection probability (![]() ). Regarding the fact (i), a rise in
). Regarding the fact (i), a rise in ![]() attributed to an increase in d (Proposition 4) implies a reduction of employment flows into the pool of permanent jobs with unknown match quality (unemployed workers are more likely to be hired in temporary jobs). The rise in
attributed to an increase in d (Proposition 4) implies a reduction of employment flows into the pool of permanent jobs with unknown match quality (unemployed workers are more likely to be hired in temporary jobs). The rise in ![]() also has the following impact on flows into permanent jobs with good match quality: a higher
also has the following impact on flows into permanent jobs with good match quality: a higher ![]() means a higher probability that match quality will be revealed to be good and that more workers will move from the pool of permanent jobs with unknown match quality to the pool of permanent jobs with good match quality. What is important in obtaining the result of Proposition 6 is that an increase in average productivity depends on how dismissal costs affect the hiring standard for temporary jobs. Although reducing
means a higher probability that match quality will be revealed to be good and that more workers will move from the pool of permanent jobs with unknown match quality to the pool of permanent jobs with good match quality. What is important in obtaining the result of Proposition 6 is that an increase in average productivity depends on how dismissal costs affect the hiring standard for temporary jobs. Although reducing ![]() by increasing d, which occurs in Proposition 5, reduces the number of workers who move from the pool of temporary jobs to the pool of permanent jobs with good match quality, the proportion of jobs with good quality among permanent jobs
by increasing d, which occurs in Proposition 5, reduces the number of workers who move from the pool of temporary jobs to the pool of permanent jobs with good match quality, the proportion of jobs with good quality among permanent jobs ![]() increases. This phenomenon occurs because more workers become temporary employees because of the reduction in
increases. This phenomenon occurs because more workers become temporary employees because of the reduction in ![]() and permanent workers tend to have experienced temporary jobs. Because only temporary jobs that are revealed to have good match quality are converted into permanent contracts, the reduction in
and permanent workers tend to have experienced temporary jobs. Because only temporary jobs that are revealed to have good match quality are converted into permanent contracts, the reduction in![]() , which reduces the ratio of permanent workers in the pool of matches with unknown productivity, increases
, which reduces the ratio of permanent workers in the pool of matches with unknown productivity, increases![]() . Regarding the fact (ii), a higher hiring threshold for permanent jobs increases the possibility that the true quality of a match is good. This contributes to the higher average productivity of permanent jobs.
. Regarding the fact (ii), a higher hiring threshold for permanent jobs increases the possibility that the true quality of a match is good. This contributes to the higher average productivity of permanent jobs.
We here examine how the dismissal costs for permanent jobs affect the average productivity of temporary jobs and the ratio of temporary employment. Regarding the average productivity of temporary jobs, we obtain the following proposition:
Proposition 7. An increase in dismissal costs has an ambiguous impact on the average productivity of temporary jobs.
Proof. See Appendix G.
The reason for this result is that increasing dismissal costs has two opposite effects: a decline in the hiring threshold for temporary jobs and an increase in the hiring threshold for permanent jobs. The former effect results in the decreased average productivity of temporary jobs, whereas the latter effect helps to increase average productivity. Therefore, a change in average productivity depends on which effect overcomes the other.
Furthermore, it follows from (30) and (31) that the relative ratio of temporary employment is expressed by
![]()
where ![]() is defined as
is defined as
![]()
Simple calculations show that an increase in d increases this ratio. Therefore, higher firing costs for permanent jobs increase the proportion of temporary employment. This result is consistent with the finding by [33] that showed that more stringent protection of workers on open-ended contracts increases the reliance on fixed- term contracts by employers aiming to achieve their desired levels of worker turnover.
The qualitative analysis conducted in this paper suggests that reducing dismissal costs for permanent jobs increases job creation and the proportion of permanent employment when match productivity is more dispersed (z is large). Using a similar framework, [13] finds that the increased use of temporary contracts is a second-best solution relative to reducing permanent employment protection: the latter policy will have a stronger impact on unemployment and social welfare than will reducing employment protection for temporary workers.17 Although policies of easing employment protection for permanent jobs appear to be problematic because of political pressure from permanent workers (see [35] ), these policies will be the first choice if they are viable.18 However, we should emphasise that Proposition 6 suggests that the favourable effects of weakening employment protection for permanent jobs will be in exchange for reducing the average productivity of permanent jobs when match productivity is more dispersed. In other words, if temporary contracts are expected to screen workers before they are promoted to permanent employment, increasing labour market flexibility by reducing dismissal costs for permanent jobs makes this screening role less significant because employers become less selective in hiring workers as permanent employment and the proportion of matches with unknown productivity increases.
We finally note the finding of [3] that fixed-term contracts are used as devices for screening workers for permanent positions, especially in uncertain economic environments. Although we must be careful when using the word “uncertain”, statements in Proposition 4 and Proposition 5 are consistent with their finding in the sense that temporary contracts are likely to become a major route to obtaining permanent positions (![]() increases and
increases and ![]() decreases for a sufficiently higher z). On that basis, these propositions show how the impact of changing dismissal costs on employers’ hiring decisions is affected by the uncertainty in productivity. Together with the effectiveness of the screening role of temporary contracts, policy makers should take into account the effect of employment protection legislation on employers’ hiring strategies regarding both permanent and temporary contracts in a given uncertain economic environment.
decreases for a sufficiently higher z). On that basis, these propositions show how the impact of changing dismissal costs on employers’ hiring decisions is affected by the uncertainty in productivity. Together with the effectiveness of the screening role of temporary contracts, policy makers should take into account the effect of employment protection legislation on employers’ hiring strategies regarding both permanent and temporary contracts in a given uncertain economic environment.
5. Conclusions
This paper has examined how the employment protection of permanent contracts affects employers’ hiring decisions if the true productivity of a worker-firm pair is not fully revealed even after a match is formed. We incorporate permanent and temporary contracts into an equilibrium search model and consider a situation in which temporary contracts are used to screen workers for permanent positions. Although employers cannot accurately observe the true quality of a match, they receive an observable signal about the quality of the match when hiring a worker. Employers’ hiring decisions are based on the realisation of this signal and are characterised as the determination of the hiring thresholds. The innovative point of this paper is that employers’ choice of what type of contract to offer is endogenous. This enables us to specify the hiring threshold for each type of employment contract and to analytically examine the impact of a change in dismissal costs on each threshold and labor productivity.
The main results obtained in this paper are summarised as follows. First, there exists a unique steady-state equilibrium in which employers have an incentive to offer permanent contracts and both permanent and temporary jobs exist concurrently. Second, reducing dismissal costs for permanent jobs increases job creation. Third, higher dismissal costs reduce the hiring threshold for temporary jobs and raise the threshold for permanent jobs, which implies that employers will be more (less) selective in hiring workers for permanent (temporary) employment when dismissal costs increase. We also note that the responses to these hiring thresholds occur under a high degree of uncertainty about the more true quality of job matches. In this situation, temporary contracts are likely to be used as screening devices, and therefore, the impact of dismissal costs varies between permanent and temporary contracts. Fourth, increasing dismissal costs increases the average productivity of permanent jobs when the hiring threshold for temporary jobs is reduced and that for permanent jobs is raised. These results imply that increasing labour market flexibility by reducing dismissal costs for permanent jobs has an adverse effect of reducing the screening function of temporary contracts and lowering the average productivity of permanent jobs, whereas this policy appears to have favourable effects such as fostering job creation and increasing the proportion of permanent workers.
Acknowledgements
I thank the Editor and the referee for their comments. I am also very grateful to Hiroaki Miyamoto and the participants in the Search Theory Workshop at Hokkaido University and the 26-th EALE conference in Ljubljana for their helpful comments. This work was partly supported by JSPS KAKENHI Grant Number 29014289. All remaining errors are mine.
Appendix
Appendix A. Proof of Proposition 1
We prove the statements of the proposition by relying on the following three facts: (i) ![]() is strictly less than
is strictly less than![]() ; (ii)
; (ii) ![]() is strictly greater than
is strictly greater than![]() ; and (iii)
; and (iii) ![]() is strictly less than zero, where
is strictly less than zero, where ![]() is given by (18).
is given by (18).
First, it follows from (12) and (16) that ![]() becomes
becomes
![]() (A-1)
(A-1)
If (19) is satisfied, the first term in (A-1) and the overall sign of (A-1) are negative.
Second, from (11), we obtain
![]() (A-2)
(A-2)
We note that from (13) and (15), ![]() is represented by
is represented by
![]() (A-3)
(A-3)
Substituting (A-3) into (A-2) and arranging it yield
![]() (A-4)
(A-4)
This takes a non-negative value if (20) holds. Since both ![]() and
and ![]() are linear and increasing in
are linear and increasing in![]() , there exists a unique
, there exists a unique ![]() that satisfies (17).
that satisfies (17).
Finally, we will show that ![]() is strictly greater than
is strictly greater than![]() . To prove this statement, it is sufficient to show that
. To prove this statement, it is sufficient to show that ![]() has a negative sign because the slope of
has a negative sign because the slope of ![]() is larger than that of
is larger than that of ![]() for any
for any![]() .19 Evaluating (9) by
.19 Evaluating (9) by ![]() and substituting (18) into it result in
and substituting (18) into it result in
![]()
We can show that the first term of the brace in (A-5) is less than one. Because the second term of the brace in (A-5) is obviously greater than one, the overall sign of (A-5) is negative. This indicates that ![]() is less than
is less than ![]() at
at ![]()
![]() . The proof is complete.
. The proof is complete.
Appendix B. Proof of Lemma 1
We first show that the coefficient of the last term of the brace in (38) is less than one. Actually, we obtain
![]()
We also note that the following inequality stems from (20):
![]() (B-1)
(B-1)
Thus the sum of the first and the last terms in the brace of (38) has a positive sign and the overall sign of (38) is also positive. The proof is complete.
Appendix C. Proof of Proposition 3
The second term of (39) takes a negative value from Lemma 1 and![]() . (37) ensures that the third term of (39) also has a negative sign. Although the last term is positive because
. (37) ensures that the third term of (39) also has a negative sign. Although the last term is positive because![]() , this becomes quite small for a sufficiently high
, this becomes quite small for a sufficiently high ![]() because
because
![]()
Under the fact that![]() , the overall sign of (39) is likely to be negative.
, the overall sign of (39) is likely to be negative.
Recalling that the LHS of (21) is increasing and the RHS of (21) is decreasing in![]() , we finally find that an increase in d decreases
, we finally find that an increase in d decreases![]() . The proof is complete.
. The proof is complete.
Appendix D. Proof of Proposition 4
We first note that the following facts are obtained for a given![]() :
:
(i) (17’) yields
![]()
where
![]()
Arranging the terms in the brace of the above equation results in
![]() (D-1)
(D-1)
(ii) It follows from (38) that we obtain
![]() (D-2)
(D-2)
where
![]()
(iii) The expressions of ![]() and
and![]() , which are described in subsection 3.2, yield
, which are described in subsection 3.2, yield
![]() (D-3)
(D-3)
![]() (D-4)
(D-4)
(iv) It follows from (18) that we obtain
![]() (D-5)
(D-5)
where it follows from (15) that ![]() is given by
is given by
![]()
(v) (37) yields
![]() (D-6)
(D-6)
(vi) Focusing on the RHS of (21), the impact of ![]() is given by
is given by
![]() (D-7)
(D-7)
and the impact of d on the RHS of (21) for a given ![]() is given by
is given by
![]() (D-8)
(D-8)
where expressions in subsection 3.2 yield
![]() (D-9)
(D-9)
From (D-7) and (D-8), ![]() is expressed by
is expressed by
![]() (D-10)
(D-10)
At this stage, we are now ready for examining the overall effect of d on![]() . This effect is represented by
. This effect is represented by
![]() (D-11)
(D-11)
The numerator of (D-11) is given by
![]() (D-12)
(D-12)
In this equation, note that the first term of (D-12) takes a negative sign because of the result of Lemma 1 and![]() . A sign of the last term is also negative because
. A sign of the last term is also negative because
![]()
We then focus on the square brackets of the second and the third term of (D-12). Regarding the second term, it follows from (D-3) and (D-9) that we obtain
![]()
Using (D-1) and (D-2), this expression is rewritten as
![]() (D-13)
(D-13)
Since a sign of (D-13) depends on a sign of its second line, we will specify the condition which makes the latter positive. Arranging the second line of (D-13) yields
![]() (D-14)
(D-14)
In the derivation of the second line, we have used the fact that the expression
![]()
around ![]() (this is actually less than one if
(this is actually less than one if![]() ). Then, the first line of (D-14) takes a positive sign if the following condition holds:
). Then, the first line of (D-14) takes a positive sign if the following condition holds:
![]() (D-15)
(D-15)
Using the definition of![]() , (D-15) is rewritten as (42), where its denominator takes a positive sign if (40) holds.
, (D-15) is rewritten as (42), where its denominator takes a positive sign if (40) holds.
Regarding the square bracket of the third term of (D-12), it follows from (D-1), (D-2), (D-5) and (D-6) that we obtain
![]() (D-16)
(D-16)
Arranging the terms in the brace of (D-16) yields
![]() (D-17)
(D-17)
The coefficient of ![]() in (D-17) is expressed by
in (D-17) is expressed by
![]()
Substituting this into (D-17) yields
![]() (D-18)
(D-18)
To identify a sign of (D-18), we first compare the term in the second brace of the first line with the coefficient of the second line:
![]()
where we have used the fact that![]() . This has a non-negative sign if the following condition holds:
. This has a non-negative sign if the following condition holds:
![]() (D-19)
(D-19)
Using the definition of![]() , we can rewrite (D-19) as
, we can rewrite (D-19) as
![]() (D-19’)
(D-19’)
Since (41) ensures that the denominator of (D-19’) takes a positive sign, (D-19’) (equivalently, (D-19)) is redundant.
Second, comparing the term in the first brace of the first line of (D-18) with the term in the brace of its second line yields
![]()
This takes a non-negative sign if
![]() (D-20)
(D-20)
Using the definition of![]() , the condition (43) is obtained.
, the condition (43) is obtained.
Therefore, under the conditions (D-15), (D-19) and (D-20), (D-12) takes a negative sign.20 Then, we conclude that an increase in dismissal costs for permanent jobs raises the hiring threshold of permanent jobs (recall that the denominator of (D-11) is equivalent to that of (D-10) and its sign is negative). The proof is complete.
Appendix E. Proof of Proposition 5
The overall effect of d on ![]() is represented by
is represented by
![]()
Its numerator is written by
![]() (E-1)
(E-1)
First, it follows from (D-3), (D-5), (D-6) and (D-9) that the terms in the parenthesis of the second term in (E-1) are given by
![]()
This takes a positive sign if the following condition holds:
![]() (E-2)
(E-2)
Second, it follows from (D-1), (D-2), (D-5) and (D-6) that the terms in the parenthesis of the third term in (E-1) are given by
![]() (E-3)
(E-3)
In (E-3), the coefficient of ![]() is arranged as follows:
is arranged as follows:
![]()
Substituting this expression into the brace in (E-3) yields
![]() (E-4)
(E-4)
We first specify the condition which makes the following expression positive:
![]() (E-5)
(E-5)
A sign of (E-5) becomes non-negative if the following condition is satisfied:
![]() (E-6)
(E-6)
Since the condition (20) is more binding than (E-6), this condition is redundant. Subsequently, we examine a sign of the following expression from (E-4) and obtain the condition which makes it non-negative:
![]() (E-7)
(E-7)
Since ![]() is less than one, the RHS of (E-7) is strictly greater than the RHS of (E-2). This means that (E-7) is redundant if the condition (E-7) is satisfied. Under (E-7), a sign of (E-4) is negative. Note that since the RHS of (E-7) is increasing with respect to
is less than one, the RHS of (E-7) is strictly greater than the RHS of (E-2). This means that (E-7) is redundant if the condition (E-7) is satisfied. Under (E-7), a sign of (E-4) is negative. Note that since the RHS of (E-7) is increasing with respect to![]() , it is likely to be satisfied for a small
, it is likely to be satisfied for a small![]() .21 Rewriting (E-7) by using the definition of
.21 Rewriting (E-7) by using the definition of ![]() yields
yields
![]() (E-7’)
(E-7’)
Finally, we consider the impact of the first and the last term of (E-1). Regarding the first term, it has a smaller impact on (E-1) if (i) the expected costs of having a vacancy are less affected by a change in![]() ; (ii)
; (ii) ![]() is sufficiently small. The condition (i) is straightforward because
is sufficiently small. The condition (i) is straightforward because ![]() results from the LHS of (21). Regarding the condition (ii), it follows from (D-6) that we can show that the direct impact of d on
results from the LHS of (21). Regarding the condition (ii), it follows from (D-6) that we can show that the direct impact of d on ![]() decreases as
decreases as ![]() becomes smaller:
becomes smaller:
![]() (E-8)
(E-8)
where the last line of (E-8) takes a positive sign if the following inequality holds:
![]() (E-9)
(E-9)
Regarding the last term of (E-1), we note that the impact of ![]() decreases as
decreases as ![]() becomes smaller. This result is easily obtained as follows. It follows from (D-4) with
becomes smaller. This result is easily obtained as follows. It follows from (D-4) with ![]() that
that
![]()
Together with fact that the direct impact of d on ![]() decreases as
decreases as ![]() becomes smaller, the last term of (E-1) also has a smaller impact for a sufficiently small
becomes smaller, the last term of (E-1) also has a smaller impact for a sufficiently small![]() . Using these results, we conclude that (E-1) is likely to have a positive sign. The proof is complete.
. Using these results, we conclude that (E-1) is likely to have a positive sign. The proof is complete.
Appendix F. Proof of Proposition 6
Let us define the conditional expectations of ![]() under
under ![]() and under
and under![]() , respectively. Note that
, respectively. Note that ![]() has been already defined as
has been already defined as
![]() (F-1)
(F-1)
and let us define ![]() as
as
![]() (F-2)
(F-2)
Using (F-1) and (F-2), the average productivity of permanent jobs is expressed by
![]() (F-3)
(F-3)
To examine the effect of d on (F-3), we focus on the effect of d on ![]() and
and![]() . First, it follows from (30) and (32) that
. First, it follows from (30) and (32) that ![]() is represented by
is represented by
![]() (F-4)
(F-4)
where
![]()
![]()
![]()
![]()
It follows from these facts and (F-4) that ![]() has an equal sign to the following expression:
has an equal sign to the following expression:
![]() (F-5)
(F-5)
A sign of (F-5) is positive if ![]() and
and![]() . Thus, higher dismissal costs increase the proportion of good type matches among permanent jobs, provided that the conditions for Proposition 4 and Proposition 5 are satisfied.
. Thus, higher dismissal costs increase the proportion of good type matches among permanent jobs, provided that the conditions for Proposition 4 and Proposition 5 are satisfied.
We next examine how an increase in d affects![]() . From the definition of
. From the definition of![]() , which is given by (F-1), we obtain
, which is given by (F-1), we obtain
![]() (F-6)
(F-6)
Using (F-3), (F-5) and (F-6), we conclude that an increase in d increases the average productivity of permanent jobs. The proof is complete.
Appendix G. Proof of Proposition 7
The average productivity of temporary jobs is represented by
![]()
where the expression of ![]() is given in (F-2). Contrary to the definition of the average productivity of permanent jobs, the average productivity of temporary jobs is simply described because all temporary jobs in this model has unknown productivity. Thus, it suffices to examine the effect of d on
is given in (F-2). Contrary to the definition of the average productivity of permanent jobs, the average productivity of temporary jobs is simply described because all temporary jobs in this model has unknown productivity. Thus, it suffices to examine the effect of d on![]() . Partially differentiating
. Partially differentiating ![]() with respect to d yields
with respect to d yields
![]() (G-1)
(G-1)
Note that the square bracket in the first line has a positive sign, while the square bracket in the second line has a negative sign. Using the results obtained in Proposition 4 and Proposition 5, the overall sign of (G-1) is indeterminate. The proof is complete.
![]()
Submit your manuscript at: http://papersubmission.scirp.org/
NOTES
![]()
1 [5] present evidence that temporary work is a stepping stone to permanent work depending on the type of contract and the employee’s gender. [6] find that a job at a temporary work agency may be an effective springboard to a permanent contract in Europe, although not in the US.
2 [8] address the issue of whether there are performance differences between establishments that use temporary agency workers as buffer stock (called the flexibility strategy) and establishments that use them for screening purposes. They conclude that the productivity of establishments that use the flexibility strategy is significantly lower than that of establishments that use the screening strategy.
3As noted in [10] , the quality of a match is considered to be imperfectly observable at the stage of forming the match, and therefore, employers learn about the true quality of the match through production activity. Based on the notion that some aspects of a worker-firm match can only be revealed after the employment relationship has been established, [11] focus on the difference in the learning process between learning about match quality and learning-by-doing and examine how an economy’s average productivity is affected by imposing dismissal costs. Using a model of heterogeneous workers that incorporates search frictions and endogenous separations of employment matches, [12] examine how worker heterogeneity amplifies unemployment fluctuations depending on the size of gross labour flows and asymmetric productivity shocks. In their model, a worker’s type is revealed by interviewing and screening in the job search and recruitment process.
4Multiple studies extend the framework of [14] . [15] incorporates job-specific shocks and examines the impact of employment protection on labour productivity. [16] focus on the screening effect of temporary jobs on transitions to regular employment. In their model, the effects of hiring and firing subsidies on the unemployment rate and social welfare are examined. [17] investigates the conditions under which temporary jobs are stepping stones to permanent jobs.
![]()
5 [18] develop a matching model in which adverse selection and firing costs are incorporated, examining reemployment probabilities for employed and unemployed workers. Because employers can only observe worker quality imperfectly, they may hire workers with poor match quality. Kugler and Saint-Paul show that introducing unjust dismissal provisions reduces the reemployment probabilities of unemployed job seekers but not those of employed job seekers.
6 [19] uses the two-period model to investigate the impact of easing the creation of temporary jobs and shows that temporary contracts are more advantageous for employers during recessions than booms. [20] extend [9] , incorporating on-the-job searches and permanent and temporary contracts into their model. They characterise the equilibrium in which permanent workers choose not to search but temporary workers decide to search. Then, employers have a risk of losing workers and having vacancies if they offer temporary contracts. [21] incorporate temporary and permanent jobs into a matching model with directed search. In their model, employers are willing to offer permanent contracts because the rate of filling permanent jobs is higher than that for temporary jobs.
7Although our assumption that temporary contracts last for only one period appears to be extreme, [22] note that in France, the average duration of temporary jobs is quite short (roughly one and a half months). They construct a job search and matching model with different expected durations to capture employer choices regarding the forms of contracts. In this paper, we will show that certain conditions are necessary to ensure that firms prefer permanent to temporary contracts even in such extreme situations. Furthermore, we also note that the main results of this paper do not change essentially if temporary employment is allowed to continue with some constant probability.
8The effects of various employment protection reforms on productivity and TFP have recently been investigated. See [23] - [26] , for example.
![]()
9“Match-specific” means that the productivity of each match depends on a worker whom an employer meets in the search process.
10The relative size and importance of each component (the firing tax component and the transfer component) differ across countries. [28] posit that the transfer component is not negligible in Italy, whereas the tax component of dismissal costs is considered to be substantially larger than the transfer component. They argue that the neutrality of severance payments, which was shown by [29] , continues to hold in their framework.
![]()
11 [31] assume that a temporary job is either terminated or converted into a permanent job in the next period. [13] assumes that a match of unknown type in a temporary job can be either retained or converted into a permanent job in the next period. In his model, even matches with high productivity will be retained in temporary form.
12The strictly positive sign of ![]() is required for the fact that permanent jobs are profitable for any
is required for the fact that permanent jobs are profitable for any![]() . This condition is satisfied if
. This condition is satisfied if
13In the later section, we will show that an increase in d decreases the equilibrium value of![]() . Therefore, we interpret that the condition (19) requires dismissal costs for permanent jobs to be lower.
. Therefore, we interpret that the condition (19) requires dismissal costs for permanent jobs to be lower.
14According to [32] , the share of fixed-term contracts in new hires reached approximately 91 - 95 per cent during 1985-2002 in Spain. This tendency is also observed in other European countries in which restrictions on the use of fixed-term contracts have been relaxed, as in France.
15A boundary condition at ![]() is necessary for the existence of a unique intersection between the locus of the LHS of (21) and that of the RHS of (21). Because
is necessary for the existence of a unique intersection between the locus of the LHS of (21) and that of the RHS of (21). Because ![]() goes to one as
goes to one as ![]() goes to zero, either high recruiting costs or strong worker bargaining power must be present to obtain the conclusion that the locus of the LHS of (21) lies below its RHS.
goes to zero, either high recruiting costs or strong worker bargaining power must be present to obtain the conclusion that the locus of the LHS of (21) lies below its RHS.
![]()
16The result that higher dismissal costs reduce the hiring threshold for temporary jobs is noted in [17] as well. However, [17] obtains this result through calibration, and therefore the conditions for which this result holds are not specified. [13] examines the welfare effects of introducing employment protection in the form of dismissal costs and the liberalisation of temporary contracts and does not focus on how changing dismissal costs affects hiring thresholds.
![]()
17 [34] derives the analytical expression of TFP by using the equilibrium search model with endogenous job destruction, and he shows that introducing firing costs enables low-productivity jobs to survive and reduces TFP.
18 [24] address the topic of a reform implemented in Austria in 2003. In Austria, a system of individual savings accounts has been introduced for regular jobs rather than redundancy pay. According to this study, there is little opposition to this reform from regular workers, and it has resulted in a drop in the employment protection legislation indicator for those workers.
19This fact is obtained by differentiating (16) with respect to ![]() and using
and using![]() .
.
20We note that ![]() and
and ![]() from (D-4).
from (D-4).
21Although ![]() is composed of
is composed of ![]() and
and![]() , a change in
, a change in ![]() directly affects the condition itself. We thus focus on a change in z when discussing the impact of
directly affects the condition itself. We thus focus on a change in z when discussing the impact of![]() .
.