
Subject Areas: Theoretical Physics
1. Introduction
A basic implication of Maxwell’s theory is that, all electromagnetic radiations propagate in vacuum at a constant velocity c. This conclusion was further raised to the postulate of special relativity, and soon after that described successfully as the moving behavior of massless photon by quantum theory. Despite all these, a substantial experimental effort [1] [2] has been made to measure the mass of photon 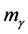 (we shall see below that, for being determined by unit spin
(we shall see below that, for being determined by unit spin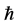 ,
, 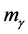 would be treated as the spin (or effective) mass of photon rather than the conventional one; it is noticed that its conventional mass is still zero). If the effective mass of photon was found to be nonzero, it would produce an effect on the contemporary physical theories [3] [4] ; for example, the special relativity must be modified to suit massive photon [5] .
would be treated as the spin (or effective) mass of photon rather than the conventional one; it is noticed that its conventional mass is still zero). If the effective mass of photon was found to be nonzero, it would produce an effect on the contemporary physical theories [3] [4] ; for example, the special relativity must be modified to suit massive photon [5] .
Now, it is considered to be almost certainly impossible to do any experiment to confirm the value of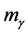 . The best one can hope to do is to place ever tighter limits on its size, since it might be so small that none of the present experimental strategies could detect it. According to the uncertainty principle, the ultimate upper limit on
. The best one can hope to do is to place ever tighter limits on its size, since it might be so small that none of the present experimental strategies could detect it. According to the uncertainty principle, the ultimate upper limit on 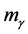 is estimated to be
is estimated to be , as taking the time uncertainty
, as taking the time uncertainty  of the universe age of about 1010 years [1] . Although such an infinitesimal mass would be extremely difficult to detect, there are still some implications, such as a Yukawa type of potential, a frequent dependence of light speed, to be worth paying attention, and all of these have been studied seriously [6] . All the works in this area have opened a door to useful approaches for laboratory experiments or cosmological observations aimed at determining the effective mass of photon or, more precisely, setting an upper limit on it. And from the standpoint of testing for a photon mass, the key point, as a direct consequence of nonzero photon mass, is one of searching for frequency dispersion of the speed of light [1] . For example, The results of several pulsar measurements by Bay and White [7] placed a rough upper limit on the photon mass of
of the universe age of about 1010 years [1] . Although such an infinitesimal mass would be extremely difficult to detect, there are still some implications, such as a Yukawa type of potential, a frequent dependence of light speed, to be worth paying attention, and all of these have been studied seriously [6] . All the works in this area have opened a door to useful approaches for laboratory experiments or cosmological observations aimed at determining the effective mass of photon or, more precisely, setting an upper limit on it. And from the standpoint of testing for a photon mass, the key point, as a direct consequence of nonzero photon mass, is one of searching for frequency dispersion of the speed of light [1] . For example, The results of several pulsar measurements by Bay and White [7] placed a rough upper limit on the photon mass of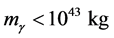 .
.
In quantum field theory [8] , the electromagnetic fields (EFs) have been successfully described as the neutral massless photon with unit spin . However, for massive photon [9] [10] , it would require a set of new equations, which was proposed by Proca at first [11] . In Proca theory, the Lorentz condition is automatically held, but gauge invariance would be inevitably lost. So that, once the photon was confirmed to be massless, no matter large or small, it would have a bearing on some fundamental physical questions [5] [12] . In Section 2, we will establish a set of new equations to describe massive electromagnetic fields (MEFs), whose consequent distinctness compared with purely Maxwell equivalents is presented. In Section 3, the wave solutions of MEFs are given, which can naturally lead to the Hubble redshift in cosmology. Sections 4 and 5 introduce the developed relativity and massive electrodynamics; Section 6 presents the Dirac typical equation of massive photon.
. However, for massive photon [9] [10] , it would require a set of new equations, which was proposed by Proca at first [11] . In Proca theory, the Lorentz condition is automatically held, but gauge invariance would be inevitably lost. So that, once the photon was confirmed to be massless, no matter large or small, it would have a bearing on some fundamental physical questions [5] [12] . In Section 2, we will establish a set of new equations to describe massive electromagnetic fields (MEFs), whose consequent distinctness compared with purely Maxwell equivalents is presented. In Section 3, the wave solutions of MEFs are given, which can naturally lead to the Hubble redshift in cosmology. Sections 4 and 5 introduce the developed relativity and massive electrodynamics; Section 6 presents the Dirac typical equation of massive photon.
2. Massive Electromagnetic Field Equations
In Maxwell’s theory, electromagnetic phenomena are always characterized by the electric and magnetic fields (E, B), which are thought of as the quantum of light in term of photon. If photon is massive instead of massless, its motion equations would become Proca form (in the Heaviside-Lorentz system of units) [13] [14]
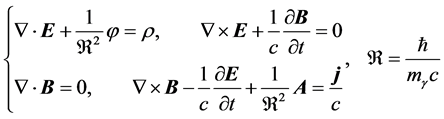 (2.1)
(2.1)
where, 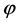 , A denote the electromagnetic potentials,
, A denote the electromagnetic potentials, 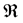 indeed reflects the effective range of electromagnetic interaction. After that, Proca equations (PEs) have provided the pathway for almost all approaches to detect the photon mass. Specifically, due to
indeed reflects the effective range of electromagnetic interaction. After that, Proca equations (PEs) have provided the pathway for almost all approaches to detect the photon mass. Specifically, due to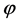 , A being observable, Proca theory would lose its proper gauge invariance. Because of the nonzero photon mass, the dispersion produces a frequency dependence [15]
, A being observable, Proca theory would lose its proper gauge invariance. Because of the nonzero photon mass, the dispersion produces a frequency dependence [15]
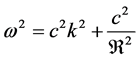 (2.2)
(2.2)
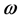 is the angular frequency, k the wave number. This frequent dependence could be used to determine the photon mass in experiments [16] [17] .
is the angular frequency, k the wave number. This frequent dependence could be used to determine the photon mass in experiments [16] [17] .
The quantum theory can provide a basis for massive electromagnetic theory, since according to the theory, vacuum is not empty, but filled with a large number of virtual particle-antiparticle pairs flashing in and out of existence [18] . Generally, these pairs may not bring any effect, whereas in the presence of external fields, they could be pulled away directionally. Such the situation strongly suggests that, the vacuum should be treated as a kind of dielectric, and thus, when the external fields applied, the polarization charge 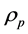 and current
and current 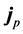 are produced. To take account of the physical consequence of vacuum polarization, we need to rewrite MEs as
are produced. To take account of the physical consequence of vacuum polarization, we need to rewrite MEs as
![]() (2.3)
(2.3)
These equations can be further expressed in 5-dimensional Minkowski space with an extra-dimension ![]() identified with the spin phase of moving particle (see Figure 1). The whole 5-dimensional manifold is described by the space-phase-time coordinates
identified with the spin phase of moving particle (see Figure 1). The whole 5-dimensional manifold is described by the space-phase-time coordinates![]() , similar to the space-time-mass suggested by Wesson [19] . Specifically, the value of
, similar to the space-time-mass suggested by Wesson [19] . Specifically, the value of ![]() should be very small, since the law of causality requires
should be very small, since the law of causality requires![]() , and the examining region also far less than the interaction range, i.e.
, and the examining region also far less than the interaction range, i.e.![]() .
.
Now, we introduce a polarized vector field ![]() and a polarized scalar field b by
and a polarized scalar field b by
![]() (2.4)
(2.4)
and note that, the positive and negative charge elements ![]() may appear deviation, i.e.
may appear deviation, i.e. ![]() . Although this kind of relative deviation is quite impressively small, whose currently accepted upper limit only
. Although this kind of relative deviation is quite impressively small, whose currently accepted upper limit only ![]() [20] , as long as not be zero, then every produced pair will bring out an extra charge
[20] , as long as not be zero, then every produced pair will bring out an extra charge![]() . And hence, there exists the following flow equation
. And hence, there exists the following flow equation
![]() (2.5)
(2.5)
where ![]() denotes the gradient operator of 4-dimensional generalized space
denotes the gradient operator of 4-dimensional generalized space![]() ,
, ![]() the added current flowing along f-axis, responsible for the charge deviation. The equation together with Equation (2.3) gives a generalized form of charge conservation
the added current flowing along f-axis, responsible for the charge deviation. The equation together with Equation (2.3) gives a generalized form of charge conservation
![]() (2.6)
(2.6)
It shows that, the charge is conserved in space![]() , but slightly non-conserved in
, but slightly non-conserved in ![]() due to
due to![]() . In view of this, we here develop MEs into
. In view of this, we here develop MEs into
![]() (2.7)
(2.7)
called generalized Maxwell’s equations (GMEs). The performance of massive electromagnetic induction can be summarized as follows:
1) Varying magnetic and polarized scalar fields generate respectively an electric and a polarized vector fields, described by Equations (b) and (e).
2) Varying electric field generates a magnetic field and a polarized vector field, by Equation (d).
3) Varying polarized vector field generates a polarized scalar and an electric fields, by Equation (g).
![]()
Figure 1. The 4th coordinate f is related to particle spin.
GMEs can provide a complete and self-consistent description of electromagnetic phenomena, and help us to calculate the stress of current ![]() in MEFs
in MEFs
![]() (2.8)
(2.8)
with
![]() (2.9)
(2.9)
![]() ,
, ![]() denote the generalized Poynting vector and mixed energy flow density,
denote the generalized Poynting vector and mixed energy flow density, ![]() the total energy density. In the case of
the total energy density. In the case of![]() , Equation (2.8) reduces smoothly to the classical form
, Equation (2.8) reduces smoothly to the classical form
![]() (2.10)
(2.10)
Now, by the 5-dimensional potential![]() , we express MEFs as
, we express MEFs as
![]() (2.11)
(2.11)
but need to supply a generalized Lorentz condition
![]() (2.12)
(2.12)
It is easy to verify that, MEFs still have gauge invariance under the generalized transformation of ![]() , namely
, namely
![]() (2.13)
(2.13)
![]() is an arbitrary scalar function. This practice can help us to write Equation (2.7) in d’Alembert’s form
is an arbitrary scalar function. This practice can help us to write Equation (2.7) in d’Alembert’s form
![]() (2.14)
(2.14)
which has the following retarded solution
![]() (2.15)
(2.15)
for current ![]() in a certain finite region of space
in a certain finite region of space![]() . It shows that, a moving charge and an alternating current element create at each point of the surrounding space the same potential which would be created by the fixed charge and direct current, the only difference being that such a potential is created at each point after a lapse of the delay time.
. It shows that, a moving charge and an alternating current element create at each point of the surrounding space the same potential which would be created by the fixed charge and direct current, the only difference being that such a potential is created at each point after a lapse of the delay time.
3. Implications of Massive Photon
3.1. The Yukawa Potential
The first consequence of MEFs is related to a static electric field, that is, under the static condition of![]() , Equation (2.14) reduces to
, Equation (2.14) reduces to
![]() (3.1)
(3.1)
For a point charge![]() , it yields a Yukawa typical potential
, it yields a Yukawa typical potential
![]() (3.2)
(3.2)
with an exponential decay range of![]() . The exponential deviation from Coulomb’s law will provide many approaches to test for the photon mass in laboratory experiments.
. The exponential deviation from Coulomb’s law will provide many approaches to test for the photon mass in laboratory experiments.
3.2. The Dispersion of Light
It is important that, the electromagnetic induction described by Equation (2.7) can make MEFs spread in vacuum as free wave
![]() (3.3)
(3.3)
The most typical aspect of massive photon is its frequent dependence (corresponding to Equation (2.2))
![]() (3.4)
(3.4)
![]() is the angular wave number(i.e. spin quantum number) of photon,
is the angular wave number(i.e. spin quantum number) of photon, ![]() the angular wave length. Notice that, in general the two possess the quantized values, namely
the angular wave length. Notice that, in general the two possess the quantized values, namely![]() ,
,![]() . Following Equation (3.4) is the group velocity differing from the phase velocity
. Following Equation (3.4) is the group velocity differing from the phase velocity
![]() (3.5)
(3.5)
both tend to c together, only as![]() .
.
By generalized wave vector of![]() , we also obtain a 4-velocity
, we also obtain a 4-velocity
![]() (3.6)
(3.6)
where, ![]() is the generalized wave length in space
is the generalized wave length in space![]() ,
, ![]() the total wave number, by which the generalized group and phase velocities can be define as
the total wave number, by which the generalized group and phase velocities can be define as
![]() (3.7)
(3.7)
They have the same value of c. However, when projecting to the real space, the two occur immediately differentiation, since one is displayed as a direct projection, the other represents the velocity of the intersection point of wave surface and z-axis moving along the axis (see Figure 2).
From the geometric relation above, we find
![]() (3.8)
(3.8)
In the case of![]() ,
, ![]() and
and![]() . This means, at present, the photon is rest in real space, but in
. This means, at present, the photon is rest in real space, but in
![]()
Figure 2. Physical meaning of the group and phase velocities is presented in generalized space![]() .
.
generalized space moving with velocity c. Correspondingly, the two velocities along f-axis can be given by
![]() (3.9)
(3.9)
Then we have
![]() (3.10)
(3.10)
For nonzero mass ![]() particle of spin
particle of spin ![]()
![]()
![]() (3.11)
(3.11)
with a total wave number ![]()
![]() (3.12)
(3.12)
![]() denotes the Compton wave length,
denotes the Compton wave length, ![]() the Compton wave number. Now, by introducing the Compton group and phase velocities
the Compton wave number. Now, by introducing the Compton group and phase velocities
![]() (3.13)
(3.13)
we get
![]() (3.14)
(3.14)
Clearly, for the photon of zero Compton wave number![]() , it reduces to (3.10).
, it reduces to (3.10).
3.3. The Field Structures of MEWs
Maxwell’s theory points out two polarized directions, both of which are orthogonal to the propagating direction of photon. However, MEWs described by PEs would result in a third state of polarization, in which the electric field points along the line of motion, corresponding to longitudinal photon [21] . Here, we still approve the third polarized state, but emphasize that, there will be three types of electromagnetic oscillations propagating along z-axis, those are pure transverse wave (PTW), pure longitudinal wave (PLW) and longitudinal-transverse mixed wave (LTMW). These waves possess a general solution
![]() (3.15)
(3.15)
a) Pure transverse wave. For PTW with generalized potential of![]() , we have the following fields by Equation (2.7)
, we have the following fields by Equation (2.7)
![]() (3.16)
(3.16)
The determined energy flows can be written as the energy density w multiplied by its traveling velocity![]() , namely
, namely
![]() (3.17)
(3.17)
in agreement with Equation (2.9). When the polarized fields (![]() , b) are neglected, the presented will naturally reduce to the usual form. The field structure of PTW is shown as Figure 3(a).
, b) are neglected, the presented will naturally reduce to the usual form. The field structure of PTW is shown as Figure 3(a).
b) Pure longitudinal wave. Correspondingly, the potential of PLW reads![]() . The potential combining with Lorentz condition
. The potential combining with Lorentz condition
![]() (3.18)
(3.18)
gives the following nonzero field components
![]() (3.19)
(3.19)
The energy flows come mainly from the polarized fields, namely
![]() (3.20)
(3.20)
It tells us that, as a special radiation involving the polarized fields (![]() , b), PLW (only about
, b), PLW (only about ![]() of usual
of usual
![]()
Figure 3. The field structures of PTW (a) and PLW (b) (dotted arrow and black stick denote polarized vector and scalar fields).
radiation) has no classical correspondence, but represents a natural induction process: Varying polarized vector field generates the polarized scalar and electric fields, in turn, when the latter two change, the former is induced. Figure 3(b) presents the structure of PLW.
c) Longitudinal-transverse mixed wave. With regard to LTMW of potential![]() , it is easy to find the nonzero components of MEFs
, it is easy to find the nonzero components of MEFs
![]() (3.22)
(3.22)
followed by the flows just along the travelling direction of photon (see Figure 4).
![]() (3.23)
(3.23)
However, in Proca theory, the situation is completely different, since it only gives three field components
![]() (3.24)
(3.24)
with an energy flow defined by [21] [22]
![]() (3.25)
(3.25)
not along the direction of wave vector![]() . This means, with continuous transmission, the wave energy would break away from its travelling direction, and thus leads to a physically unacceptable result. Notice that, serving as a substantial basis of electromagnetic radiation, the energy flow must represent the motion of MEWs.
. This means, with continuous transmission, the wave energy would break away from its travelling direction, and thus leads to a physically unacceptable result. Notice that, serving as a substantial basis of electromagnetic radiation, the energy flow must represent the motion of MEWs.
3.4. AB and AC Effects of MEFs
A well-known topological interference effect is called AB effect, which concerns a phase shift for moving elec-
![]()
Figure 4. Due to containing all the four fields, LTMW with E, e in Oxz plane and B parallel to y-axis, possesses a more complex structure.
trons (mass![]() ) diffracting around a tube of magnetic flux [23] , and it arises from the presence of generalized vector potential
) diffracting around a tube of magnetic flux [23] , and it arises from the presence of generalized vector potential ![]() in the Lagrangian
in the Lagrangian
![]() (3.26)
(3.26)
where the vector potential ![]() for tube system of magnetic flux, can written as
for tube system of magnetic flux, can written as![]() . When an electron beam is split and then recombined, there will be a phase shift
. When an electron beam is split and then recombined, there will be a phase shift ![]() from the interference effect. Now, consider
from the interference effect. Now, consider ![]() (Lorentz condition), we have
(Lorentz condition), we have
![]() ,
,![]() (3.27)
(3.27)
![]() denotes the flow of
denotes the flow of ![]() through any surface
through any surface ![]() bounded by the closed curve l, R the distance from the solenoid to the observational location. The result contains the standard AB effect in the limit of vanishing photon mass
bounded by the closed curve l, R the distance from the solenoid to the observational location. The result contains the standard AB effect in the limit of vanishing photon mass![]() , and an additional effect predicted from
, and an additional effect predicted from![]() , is a correction for massive photon.
, is a correction for massive photon.
An extension of the AB effect was presented by Aharonov and Casher [24] , called AC effect, which emphasizes that, a neutral particle possessing a magnetic dipole moment should experience an analogous phase shift when diffracted around a line of electric charge. Consider a magnetic dipole with mass ![]() and moment
and moment ![]() diffracted around an infinitely long line of linear charge density
diffracted around an infinitely long line of linear charge density![]() , its generalized Lagrangian can be given by
, its generalized Lagrangian can be given by
![]() (3.28)
(3.28)
The corresponding phase shift of the split beam at the recombination point reads
![]() (3.29)
(3.29)
The shift for this case is shown to reduce smoothly to that of the standard AC effect in the limit of vanishing photon mass, as was observed in the neutron interferometry experiment [25] . An additional effect is predicted from
![]() (3.30)
(3.30)
where, ![]() the scalar potential of line charge system. The AC effect in massive electrodynamics was demonstrated by Fuchs [26] , neither the AB nor AC effects would provide a practical approach for bounding the photon mass in technology until now.
the scalar potential of line charge system. The AC effect in massive electrodynamics was demonstrated by Fuchs [26] , neither the AB nor AC effects would provide a practical approach for bounding the photon mass in technology until now.
3.5. Effect of Spectral Shift
Vacuum polarization field not only can delay movement of photon, but require a generalized form of flow conservation, that is![]() ,
,![]() . So that, for the plane MEWs, there should be an average steady equation
. So that, for the plane MEWs, there should be an average steady equation
![]() (3.31)
(3.31)
with a damping solution
![]() (3.32)
(3.32)
![]() is the mean number density of photon. With the help of this solution, we can write the spectral shift of photon in unit distance as
is the mean number density of photon. With the help of this solution, we can write the spectral shift of photon in unit distance as
![]() (3.33)
(3.33)
Such the effect was first discovered by Hubble in astronomical observation [27] , that is formulated as Hubble law: the recession velocity of celestial body ![]() determined by spectral redshift is always proportional to its distance r i.e.
determined by spectral redshift is always proportional to its distance r i.e. ![]() with a ratio H called Hubble constant. Taking the observational value [28] of
with a ratio H called Hubble constant. Taking the observational value [28] of![]() , we get
, we get![]() , which has been introduced into GMEs as a natural constant like speed c.
, which has been introduced into GMEs as a natural constant like speed c.
Because of having cosmological meaning, we can use the astronomical observation (i.e. Hubble constant H) to affirm the effective mass of photon
![]() (3.34)
(3.34)
just equal to its ultimate upper limit estimated by uncertainty principle. This mass is determined by spin![]() , and so called the spin mass of photon rather than the usual one.
, and so called the spin mass of photon rather than the usual one.
4. A Generalization of Relativity for Massive Photon
Special relativity is the theory of how different observers, moving at constant velocity with respect to one another, report their experience of the same physical event. And all the descriptions are completely based on the following two postulates:
I. The laws of physics take the same form in every inertial frame;
II. The speed of light in vacuum is the same in every inertial frame.
However, in massive electromagnetic theory, the speed of light is dependent of frequency rather than a unique constant. Thus, there needs a new postulate to be proposed to restore the features of special relativity, and the proposed should be aimed at the existence of a unique limiting speed c, to which speeds of all bodies tend when their energy becomes much larger than their mass [5] [12] . Now, by the fact of that MEWs are always propagating at speed c in generalized space![]() , we introduce a modified relativistic postulate:
, we introduce a modified relativistic postulate:
The generalized speed of light is a constant c.
4.1. Generalized Lorentz Transformation
The modified postulate inspires us to discuss motion in 5-dimensional Minkowski space![]() , and write its invariant interval
, and write its invariant interval
![]() (4.1)
(4.1)
Here, the invariance means every inertial observer would obtain the same value for this particular combination. The interval ![]() is directly related to the time interval
is directly related to the time interval ![]() in the rest frame of particle with no spatial displacement
in the rest frame of particle with no spatial displacement![]() , that is
, that is![]() , or
, or
![]() (4.2)
(4.2)
The rest-frame time coordinate ![]() is called the proper time. Since there is only one rest-frame, its time interval must be unique: all observers should agree on the value, namely
is called the proper time. Since there is only one rest-frame, its time interval must be unique: all observers should agree on the value, namely
![]()
![]() (4.3)
(4.3)
gives
![]() (4.4)
(4.4)
where ![]() called generalized Lorentz factor. This is the physical basis for the invariance of the motion equation under generalized coordinate transformation.
called generalized Lorentz factor. This is the physical basis for the invariance of the motion equation under generalized coordinate transformation.
In order to contain completely such that, GMEs should keep the same form, and the modified transformation for coordinates![]() , must necessarily bring about the change of observers from frame S to
, must necessarily bring about the change of observers from frame S to ![]() moving with a generalized relative velocity
moving with a generalized relative velocity ![]() along x-axis (
along x-axis (![]() due to the frame of reference having no spin), that is
due to the frame of reference having no spin), that is
![]() (4.5)
(4.5)
GMEs have Lorentz symmetry because they are covariant under such the transformation (called generalized Lorentz transformation (GLT)), instead of the usual one.
A further 5-vector is the 5-velocity
![]() (4.6)
(4.6)
with an invariant length of
![]() (4.7)
(4.7)
Its components transform into each other under GLT in the same manner as ![]() transform into each other, namely
transform into each other, namely
![]() (4.8)
(4.8)
With the help of GLT, we can get the basic formula for velocity addition as follows:
![]() (4.9)
(4.9)
In particular, if generalized speed ![]() and
and![]() , we find
, we find
![]() (4.10)
(4.10)
This is just a restatement of the fact that, if a particle (or light) has ![]() in one frame of reference, then it has the same result of
in one frame of reference, then it has the same result of ![]() in all frames of reference. To understand physically why this is the case, it is necessary to turn to consideration of relativistic dynamics.
in all frames of reference. To understand physically why this is the case, it is necessary to turn to consideration of relativistic dynamics.
4.2. Generalized Relativistic Dynamics
In order for relativistic mechanics to be Lorentz symmetric, we need to generalize the familiar 4-momentum ![]() to the 5-dimensional form of
to the 5-dimensional form of![]() . For massive photon, it reads
. For massive photon, it reads
![]() (4.11)
(4.11)
with an invariant length of![]() , implying the conventional mass of photon is still zero. Correspondingly, for a particle with mass
, implying the conventional mass of photon is still zero. Correspondingly, for a particle with mass ![]() and spin
and spin ![]()
![]() , we have
, we have
![]() (4.12)
(4.12)
![]() is the spin to mass ratio. Obviously, for
is the spin to mass ratio. Obviously, for ![]() meson, a should be zero (due to
meson, a should be zero (due to![]() ), and for photon, infinity (due to
), and for photon, infinity (due to![]() ). Thus we see that, the linear momentum
). Thus we see that, the linear momentum![]() , spin
, spin ![]() and energy E of moving particle can naturally form a covariant 5-vector, whose components transform in a definite way under GLT: observers in relative motion will see different generalized momentum
and energy E of moving particle can naturally form a covariant 5-vector, whose components transform in a definite way under GLT: observers in relative motion will see different generalized momentum ![]() and energy E, or, as we say, the generalized momentum and energy can transform into each other.
and energy E, or, as we say, the generalized momentum and energy can transform into each other.
Moreover, we also have another 4th component of velocity
![]() (4.13)
(4.13)
The first result guarantees ![]() (consistent with our modified postulate), the second implies a
(consistent with our modified postulate), the second implies a
very small velocity ![]() for electron. Repeatedly for the earth, it reads
for electron. Repeatedly for the earth, it reads
![]() (4.14)
(4.14)
Now, by the invariant length of![]() , we can also lead to the generalized energy-momentum relation
, we can also lead to the generalized energy-momentum relation
![]() (4.15)
(4.15)
which naturally contains particle spin![]() . The presented allows us to formally take the limit of
. The presented allows us to formally take the limit of![]() , and in this limit it gives
, and in this limit it gives
![]() (4.16)
(4.16)
meaning only zero mass particle can travel at speed c in generalized space, i.e.![]() , and only zero mass particle with zero spin
, and only zero mass particle with zero spin ![]() can travel at the limit speed of
can travel at the limit speed of ![]() in real space.
in real space.
In 5-dimensional relativity, all the related concepts can be given by analogy with their corresponding relativistic versions. Thus, we define the generalized force by
![]() (4.17)
(4.17)
In the case of![]() , it reduces to the usual form. The generalized relativistic work done by
, it reduces to the usual form. The generalized relativistic work done by ![]() during a small displacement
during a small displacement![]() , can be written analogy as
, can be written analogy as
![]() (4.18)
(4.18)
The rate at which the generalized force does work is then
![]() (4.19)
(4.19)
![]() is the generalized relativistic kinetic energy. So that, integrating with respect to t gives
is the generalized relativistic kinetic energy. So that, integrating with respect to t gives
![]() (4.20)
(4.20)
By requiring that ![]() for
for![]() , we find
, we find
![]() (4.21)
(4.21)
As should be the case, the generalized energy tends to the classical form for moving particle with a small velocity![]() .
.
When particle is force-free![]() , its generalized momentum and energy conserve
, its generalized momentum and energy conserve
![]() (4.22)
(4.22)
of which, the 4th component ![]() indeed represents the spin conservation. To see the physical meaning of the above, we consider the breakup of a body (such as a radioactive nucleus) of rest mass
indeed represents the spin conservation. To see the physical meaning of the above, we consider the breakup of a body (such as a radioactive nucleus) of rest mass ![]() and spin
and spin ![]() into two pieces of rest masses
into two pieces of rest masses![]() ,
, ![]() and spins
and spins![]() ,
,![]() . If suppose the initial body is stationary, and the debris flies apart with velocities
. If suppose the initial body is stationary, and the debris flies apart with velocities ![]() and
and![]() , then some of the rest mass of the original body would be converted into the kinetic energy of the two masses produced. So by the generalized conservation laws, we have
, then some of the rest mass of the original body would be converted into the kinetic energy of the two masses produced. So by the generalized conservation laws, we have
![]() (4.23)
(4.23)
In particularly, for ![]() meson decay
meson decay![]() ,
, ![]() ,
, ![]() , it gives
, it gives
![]() (4.24)
(4.24)
Nevertheless, the truly remarkable aspect of the above conclusions is that it has its fundamental origin in the fact that there exists a universal maximum possible speed c and a characteristic length![]() , which are built into the structure of 5-dimensional Minkowski space. This structure ultimately exerts an effect on the properties of matter occupying space, phase and time, those are the linear momentum, angular momentum (spin) and energy of moving particle.
, which are built into the structure of 5-dimensional Minkowski space. This structure ultimately exerts an effect on the properties of matter occupying space, phase and time, those are the linear momentum, angular momentum (spin) and energy of moving particle.
4.3. Lagrangian Description
With ![]() in hand, it is natural to suppose that the dynamic equation for a particle with charge q and mass
in hand, it is natural to suppose that the dynamic equation for a particle with charge q and mass ![]() in MEFs is
in MEFs is
![]() (4.25)
(4.25)
By potential![]() , the equation can be transformed into
, the equation can be transformed into
![]() (4.26)
(4.26)
and further manipulated into the Lagrange’s form
![]() (4.27)
(4.27)
with the Lagrangian
![]() (4.28)
(4.28)
For zero spin particle of![]() , it reduces to the usual form
, it reduces to the usual form
![]() (4.29)
(4.29)
To derive the Hamiltonian H for charged particle in MEFs, we write the canonical momentum
![]() (4.30)
(4.30)
Then, applying Legendre transform to ![]() gives
gives
![]() (4.31)
(4.31)
Consider the energy-momentum relation ![]() and
and![]() , we have the finally Hamiltonian form
, we have the finally Hamiltonian form
![]() (4.32)
(4.32)
followed by Hamilton’s equations:
![]() (4.33)
(4.33)
These equations are first-order in time in contrast to the second-order Lagrange’s.
5. Massive Electrodynamics
It is natural that, the electrodynamics of moving bodies could be in agreement with the developed relativistic principles, under which all the related problems could be discussed. In particularly, when we say GMEs are covariant, we eventually must specify the transform properties of that, it is not only the space and time coordinates that will change, but also MEFs.
5.1. Covariant Electromagnetic Equations
The clue we need to construct a transparently covariant comes from GMEs, whose structure guarantees that the equations are form-invariant to translations in generalized space. Therefore, to show that massive electrodynamics is covariant, it is sufficient to show that the fundamental equations can be written entirely in terms of Lorentz tensors, whose components change under a Lorentz boost. The path to writing GMEs in covariant form begins with the introduction of the MEF tensor
![]() (5.1)
(5.1)
Of which, the components transform according to the rule of![]() . Tensor (5.1) can help us to express the homogeneous and non-homogeneous equations in Equation (2.7) respectively as
. Tensor (5.1) can help us to express the homogeneous and non-homogeneous equations in Equation (2.7) respectively as
![]() (5.2)
(5.2)
including continuity equation ![]() and Lorenz condition
and Lorenz condition![]() . If gauge invariance held, the Lagrangian density can be given by
. If gauge invariance held, the Lagrangian density can be given by
![]() (5.3)
(5.3)
The variation of the density with respect to ![]() yields
yields![]() .
.
Now, it is easy to confirm that, the tensor transformation rule applied to ![]() reproduces the field transformation formulae
reproduces the field transformation formulae
![]() (5.4)
(5.4)
Also noteworthy is the Lorentz invariant scalar function
![]() (5.5)
(5.5)
The presented results reflect the transform properties of MEFs. The approach can provide us all the knowledge of generalized electrodynamics.
5.2. Generalized Conservation Laws
In order to organize the conservation laws of electromagnetism, we write the stress of 5-current ![]() as
as
![]() (5.6)
(5.6)
and then get
![]() (5.7)
(5.7)
![]() denotes the generalized electromagnetic stress-energy tensor. An immediate consequence of Equation (5.7) is that a free MEF has a divergence-free stress-energy tensor
denotes the generalized electromagnetic stress-energy tensor. An immediate consequence of Equation (5.7) is that a free MEF has a divergence-free stress-energy tensor
![]() (5.8)
(5.8)
To examine the elements of![]() , we find
, we find
![]() (5.9)
(5.9)
The latter just simplifies to the negative of electromagnetic energy density w. The off-diagonal elements ![]() are proportional to the Cartesian components of the corresponding flow density defined in Equation (2.9), namely
are proportional to the Cartesian components of the corresponding flow density defined in Equation (2.9), namely
![]() (5.10)
(5.10)
A bit of algebra confirms that the space-phase components ![]() are the mixed flow density
are the mixed flow density
![]() (5.11)
(5.11)
Furthermore, the space-space components can be given by
![]() (5.12)
(5.12)
Putting all the presented results together gives the matrix of ![]() as
as
![]() (5.13)
(5.13)
With the representation (5.13) in hand, it is straightforward to confirm that Equation (5.7) contains two conservation laws in differential form. The first is a statement of the conservation of generalized momentum
![]() (5.14)
(5.14)
The second gives Poynting’s theorem of energy conservation
![]() (5.15)
(5.15)
Now, with the help of Equation (5.13), it is easy to write out the stress-energy tensor of plane MEWs discussed in Section 3, that is
![]() (5.16)
(5.16)
So, we have the following conservation equations
![]() (5.17)
(5.17)
corresponding to a steady form
![]() (5.18)
(5.18)
due to![]() . The equation implies a constant velocity, namely
. The equation implies a constant velocity, namely
![]() (5.19)
(5.19)
Treating H as the Hubble constant gives![]() , and then
, and then
![]() (5.20)
(5.20)
with ![]() representing the cosmological time. The small value of
representing the cosmological time. The small value of ![]() (e.g.
(e.g. ![]() for a
for a ![]() photon) determines that the spin phase
photon) determines that the spin phase ![]() is also a very small quantity. Notice that,
is also a very small quantity. Notice that, ![]() is nothing but the full velocity of light defined explicitly in ref [29] , which can naturally lead to Hubble redshift, in agreement with the result of Equation (3.33). Importantly, such the agreement enables us to investigate motion in full velocity space, and further introduce a modified relativistic postulate:
is nothing but the full velocity of light defined explicitly in ref [29] , which can naturally lead to Hubble redshift, in agreement with the result of Equation (3.33). Importantly, such the agreement enables us to investigate motion in full velocity space, and further introduce a modified relativistic postulate:
The generalized full speed of light is a constant c.
By the postulate, we can incorporate the presented theoretical form into a more generalized unified framework of spatial relativity [29] , the unified framework could give a satisfactory account of the relativistic phenomena.
5.3. Angular Momentum and Center of Energy
Now, by force (5.6) we define the generalized Lorentz torque density tensor as
![]() (5.21)
(5.21)
The structure of this anti-symmetric tensor is
![]() (5.22)
(5.22)
Analogous to Equation (5.7), it is possible to write the second-rank torque density as the five divergence of a generalized third-rank Lorentz tensor:
![]() (5.23)
(5.23)
The anti-symmetry of ![]() with respect to its indices
with respect to its indices ![]() implies that only 50 of its
implies that only 50 of its ![]() components are independent. In detail, we use Equations (5.7), (5.23), and the symmetry of the stress-energy tensor
components are independent. In detail, we use Equations (5.7), (5.23), and the symmetry of the stress-energy tensor ![]() to write (5.21) in the form
to write (5.21) in the form
![]() (5.24)
(5.24)
or given by
![]() (5.25)
(5.25)
We focus on the 30 components ![]()
![]() , and then find that the twenty-four with
, and then find that the twenty-four with ![]() are exactly the components of the second rank tensor of generalized angular momentum current density,
are exactly the components of the second rank tensor of generalized angular momentum current density,![]() . The six components
. The six components ![]() are similarly the components of angular momentum flow density. These six independent components can be collected into the continuity-like equation for angular momentum flow, i.e. the first of Equation (5.25). The remainders (with
are similarly the components of angular momentum flow density. These six independent components can be collected into the continuity-like equation for angular momentum flow, i.e. the first of Equation (5.25). The remainders (with![]() ) have been collected into the second.
) have been collected into the second.
Now, let us investigate the similarity between an electromagnetic pulse and a relativistic particle. When no source exists![]() , Equation (5.24) becomes
, Equation (5.24) becomes
![]() (5.26)
(5.26)
followed by the conservation equations
![]() (5.27)
(5.27)
In which, the conserved quantities are defined as the angular momentum flow densities of massive electromagnetic radiations, ![]() and
and![]() . For a single photon of generalized momentum
. For a single photon of generalized momentum![]() , we have
, we have
![]() (5.28)
(5.28)
with![]() ,
,![]() . By dispersion relation (3.4), we can get the Hamiltonian function of moving photon, that is
. By dispersion relation (3.4), we can get the Hamiltonian function of moving photon, that is
![]() (5.29)
(5.29)
It can help us to write Equation (5.27) in term of Poisson formulation (due to![]() ,
,![]() )
)
![]() (5.30)
(5.30)
with Poisson brackets defined respectively by
![]() (5.31)
(5.31)
It suggests that, when the brackets with the Hamiltonian vanish, the generalized angular momentums of moving photon will be constant.
6. Toward a Dirac Typical Equation
In this section, our aim will be try to construct a Dirac typical equation to describe the motion of photon. Along the way, we shall encounter some challenges, which ultimately will force us to a recasting of Dirac equation.
6.1. Generalized Dirac Equation
To combine relativistic invariance with quantum mechanics, let us to write out the generalized Dirac Hamiltonian of ![]() and the generalized Dirac equation (GDE)
and the generalized Dirac equation (GDE)
![]() (6.1)
(6.1)
with an explicit representation of Hermitian ![]() matrices given by
matrices given by
![]() (6.2)
(6.2)
in term of the ![]() unit I and Pauli
unit I and Pauli ![]() matrices, and
matrices, and![]() ,
, ![]() are proposed to be anticommuting matrices of square equal to one:
are proposed to be anticommuting matrices of square equal to one:
![]() (6.3)
(6.3)
To study the interaction of a Dirac particle with an external MEF characterized by potential![]() , we need to write the covariant from of GDE, that is
, we need to write the covariant from of GDE, that is
![]() (6.4)
(6.4)
where the ![]() matrices are related to
matrices are related to ![]() and
and ![]() through
through
![]() , (6.5)
, (6.5)
with ![]() Hermitian,
Hermitian, ![]() Antihermitian. The relevant coupling can be obtained from the free GDE through the coupling prescription
Antihermitian. The relevant coupling can be obtained from the free GDE through the coupling prescription![]() , that is
, that is
![]() (6.6)
(6.6)
Multiplying it by the operator ![]() yields
yields
![]() (6.7)
(6.7)
with a generalized spin tensor defined by
![]() (6.8)
(6.8)
whose components read
![]() (6.9)
(6.9)
The 10 matrices of ![]() plusing the 5 components of
plusing the 5 components of ![]() and scalar I just constitute a set of 16 linear independent
and scalar I just constitute a set of 16 linear independent ![]() matrices. Therefore, the spin coupling term can be written as
matrices. Therefore, the spin coupling term can be written as
![]() (6.10)
(6.10)
When the polarized fields neglected (i.e.![]() ,
,![]() ), it will tend to the usual result [30] .
), it will tend to the usual result [30] .
6.2. Dirac Typical Equation of Free MEW
It is easy to find the similarity between Hamiltonian (5.29) and the Dirac formation. This similarity would provide us a very useful analytical device to study the angular momentum of photon from standpoint of Dirac theory. Thus, based on the fact that, the 3rd component of photon spin is always parallel to its momentum ![]() (i.e.
(i.e.![]() ), and no zero spin photon existing, we introduce the following
), and no zero spin photon existing, we introduce the following ![]() hermitian matrices
hermitian matrices
![]() (6.11)
(6.11)
and write the generalized Hamiltonian operator of photon as
![]() (6.12)
(6.12)
where, ![]() , and thus only
, and thus only![]() ,
, ![]() are required to be anticommuting, namely
are required to be anticommuting, namely
![]() (6.13)
(6.13)
Now, it is easy to find that, the generalized angular momentum of photon ![]() is not commuting with
is not commuting with ![]()
![]() (6.14)
(6.14)
To meet the requirement, we introduce the ![]() matrices
matrices
![]() (6.15)
(6.15)
and define the generalized spin tensor of photon by![]() , with
, with
![]() (6.16)
(6.16)
The definition allows us to treat the total angular momentum ![]() as a conserved quantity rather than
as a conserved quantity rather than![]() . This conversed condition requires
. This conversed condition requires
![]() (6.17)
(6.17)
implying five conserved components, namely
![]() (6.18)
(6.18)
Accordingly, MEWs behave like relativistic particles in the sense that their angular momentum transform like the energy-momentum vector of a particle. The situation suggests the conversation law of angular momentum should be modified as: the nature of MEWs is no longer to keep the generalized![]() , but the total
, but the total ![]() (including photon spin
(including photon spin![]() ) constant. This means, only the quantities of commuting with Hamiltonian
) constant. This means, only the quantities of commuting with Hamiltonian![]() , will be the electrodynamic constants.
, will be the electrodynamic constants.
To study the physical implication of the Hamiltonian (6.12), we introduce a 5-dimensional bispinor ![]() to describe the massive electromagnetic potential, and propose the following Dirac typical equation (together with a modified Lorentz condition)
to describe the massive electromagnetic potential, and propose the following Dirac typical equation (together with a modified Lorentz condition)
![]() (6.19)
(6.19)
We here emphasize: 1) The components of ![]() must satisfy the Klein-Gordon equation, meaning a plane
must satisfy the Klein-Gordon equation, meaning a plane
MEW with ![]() (i.e.
(i.e.![]() ) is a solution. 2) There exists a 5-current density which
) is a solution. 2) There exists a 5-current density which
is conserved and whose firth component is a positive density of photon. So that, in the 5-dimensional representation (6.15), ![]() may be written as
may be written as
![]() (6.20)
(6.20)
in terms of two-component spinors ![]() and
and![]() , which satisfy
, which satisfy
![]() (6.21)
(6.21)
Solving the equation gives its eigensolutions and the corresponding eigenvalues (shown as Table 1).
![]()
Table 1. The eigensolutions of Equation (6.21).
where, the spin states ![]() and the helicity operator
and the helicity operator ![]() read respectively.
read respectively.
![]() (6.22)
(6.22)
the parameter ![]() equal to
equal to
![]() (6.23)
(6.23)
From the above, we find a 4D mixed representation of consisting of the energy symbol (±) and the spin chirality![]() , that is
, that is
![]() (6.24)
(6.24)
Then by Equation (6.19) and its conjugate form
![]() (6.25)
(6.25)
we get conservation equation
![]() (6.26)
(6.26)
The number density of photon ![]() is positive, and the density current
is positive, and the density current ![]() transforms as a generalized Lorentz 5-vector.
transforms as a generalized Lorentz 5-vector.
It is interesting to notice the equivalence between the covariant form of Equation (6.19)
![]() (6.27)
(6.27)
and the homogeneous d’Alembert’s,![]() . This equivalence allows us to express formally the MEF tensor as
. This equivalence allows us to express formally the MEF tensor as
![]() (6.28)
(6.28)
including the stress-energy one
![]() (6.29)
(6.29)
For plane MEWs of ![]() propagating along z-axis, we have Lorentz condition
propagating along z-axis, we have Lorentz condition
![]() (6.30)
(6.30)
and then get the nonzero field components (corresponding to Equation (3.22))
![]() (6.31)
(6.31)
followed by the energy density
![]() (6.32)
(6.32)
identical to expressions (3.23) and (6.26). The transverse and longitudinal fields in (6.31) represent respectively PTW and PLW, and coexistence of the both will bring us LTMW.
Up to now, we have transformed GMEs into Dirac form, which practically identical but conceptually different with the usual electrodynamics, looks upon MEWs from a viewpoint of quantum physics: MEWs are nothings but a collection of a large number of massive photon with unit spin, which can be described by a Dirac typical equation. Importantly, we find a new route that can be followed to study the motion of photon in the mathematical clothes of Dirac theory.
7. Summary
In this paper, we have made a special effort to illustrate the physical consequences of vacuum polarization. This practice could provide a direct pathway to develop Maxwell’s theory, and the development has leaded to many surprising results. To sum up, these results are:
1) The starting point of our work is to establish a set of new EFEs by the mechanism of vacuum polarization, which is expressed in generalized space with an added dimension identified with the spin phase, hence possessing gauge invariance. These equations could give us a complete and self-consistent description of electromagnetic phenomena.
2) The effects of massive photon were incorporated into electromagnetism straightforwardly through GMEs, which can be used to consider some physical implications, such as deviations in the behavior of static electromagnetic fields, the dispersion of light, the polarized states of MEWs and the Hubble redshift. In particularly, we emphatically discuss the field structures of three typical MEWs, i.e. the pure transverse, pure longitudinal and longitudinal-transverse mixed waves.
3) By a modified relativistic postulate of that: The generalized speed of light is a constant c, we develop the special relativity into a 5-dimensional Lorentz symmetric form; this form contains two natural constants: a velocity constant c and a length constant![]() . It shows that, all the relativistic problems could be considered in a space-phase-time manifold, whose components just correspond to the linear momentum, spin and energy of moving particle. In this way, the particle spin goes into the motion equation.
. It shows that, all the relativistic problems could be considered in a space-phase-time manifold, whose components just correspond to the linear momentum, spin and energy of moving particle. In this way, the particle spin goes into the motion equation.
4) To guarantee electrodynamics to be covariant, we have written entirely the fundamental equations of the subject in terms of Lorentz tensors, whose components change under a Lorentz boost, but whose essential tensor character does not change. The covariant notation provides a powerful way to organize the conservation laws of electromagnetism for the linear momentum, angular momentum and energy, including a further revisiting by Lagrangian method.
5) By reevaluating the similarity between the energy form of photon and the Hamiltonian of Dirac particle, we constructed a Dirac typical equation for free massive photon. The plane wave solutions of the equation are presented, which could bring a significant change to electrodynamics.
Finally, let us review the developed electrodynamics. The original equations (i.e. MEs) were not accurate and had to be reformulated. The modified equations (i.e. GMEs) were involved in a generalized field formulation. This field formulation always gives the same results when applied to the different frameworks, and thus the Lorentz covariance is guaranteed.