
Subject Areas: Anatomy & Physiology, Bioengineering, Biophysics, Cardiology, Radiology & Medical Imaging
1. Giriş
Hekimlik, diplomanın hak edilmesiyle birlikte mesleki girişimleri uygulama yetki ve sorumluluğunun kazanıl- dığı özel meslek gruplarından biridir. Bu nedenle, beceri artırmaya yönelik pratik uygulamalar mesleğin her döneminde eğitimin ayrılmaz parçası olmuş ve “önce zarar verme” (primum non nocere) öğretisi tartışılmaz evrensel ilke olarak kabul edilmiştir. Bu hassasiyet, çok eski dönemlerden beri “benzetim” uygulamalarının kullanılması gereğini doğurmuştur. Dilimize benzetim olarak çevrilen “simulation”, gerçek bir sistem ya da sürece ait davranışın uygun aparatlar yardımı ile taklit edildiği ve çoğunlukla da eğitim amacıyla kullanılan bir yöntem olarak bilinmektedir [1] .
Günümüz teknolojileri, biyolojik sistemlere ait davranış denklemlerinin çözümünü ve görsel materyallere dönüştürülmesini çok kolaylaştırmıştır. Bu gelişmeler de, benzetim uygulamalarının çeşitliliğinin giderek art- masına neden olmaktadır. Yenilikçi bir yaklaşım olarak “etkileşimli benzetim”, tıp eğitiminde geniş kullanım alanı bulurken [1] [2] klinik bazı uygulamalarda da, teşhis ve tedavinin yönlendirilmesinde, ilgi çeken bir yöntem olarak karşımıza çıkmaktadır [3] . Yaygın olarak kullanılan şekliyle, benzetimlerde kullanıcılar önceden tanımlanmış veya senaryolaştırılmış bilgi, soru, sorun ve durumlarla karşılaşırlar. Bundan farklı olarak, yeni teknolojiler “hastaya özel benzetim” (patient specific simulation) olarak isimlendirilen yeni uygulamaları gün- deme taşımıştır. Hastaya özel benzetimin başarılı örneklerinden biri olan vasküler patolojilerde, kan akış koşullarındaki değişimlerin nicel olarak öngörülmesine imkan sağlayan hemodinami uygulamaları bu çalış- manın konusunu oluşturmaktadır.
Günümüzde, hastaya ait anjiyografi, bilgisayarlı tomografi (CT), magnetik rezonans ve ultrasonografi gö- rüntüleri kullanılarak vasküler yapıların geometrik özelliklerinin belirlemesi ve sayısal 3-boyutlu (3D) damar modellerinin hazırlanması mümkündür [4] [5] . Mühendislik biliminin uygulamalarından biri olan “hesaplamalı akışkanlar dinamiği” (Computational Fluid Dynamics, CFD) yönteminin hazırlanan damar modeli üzerinde çalıştırılması, vasküler yapılarda kan akış koşulları ve kanın damar duvarı ile etkileşimlerini nicel olarak belir- leme ve tartışabilme imkanı sağlamıştır. Vasküler patolojinin gelişimi ve komplikasyonları ile ilgili öngörüde bulunulması, tedavinin seçimi ve planlanması, tıbbi cihaz tasarımı ve optimizasyonu konularındaki yüksek yön- lendirme potansiyeli nedeniyle oldukça güçlü ve kabul gören bir klinik araç olarak değerlendirilmektedir [4] - [7] .
Hastaya özel benzetim uygulamaları, damarın 3D gerçeğe yakın modelleri üzerindeki hemodinamik kuv- vetleri tartışmaktadır. Bu nedenle bu çalışmada, vasküler patalojilerde kan akış koşulları ve damarın yeniden şekillenmesine temel oluşturabilecek kavram ve yasalar biyofiziksel yaklaşımla tartışılmıştır [8] .
2. Teorik Arkaplan
2.1. Süreklilik Yasası
Akış borusu geometrisi ve ile akış hızı arasındaki ilişkiyi tanımlayan süreklilik yasası (Equation (1)) kütlenin korunumu ilkesini temel almaktadır. Bu yasa, viskoz bir akışkanın, silindirik bir akış borusunun farklı yarı- çaplara (r1, r2) sahip iki noktasından birim zamanda geçen hacminin (Q1, Q2) sabit olmasını gerektirmektedir (Şekil 1). Buna göre, herhangi bir nedenle damar çapının daraldığı yerde kan akış hızında (v2) artış beklen- melidir.
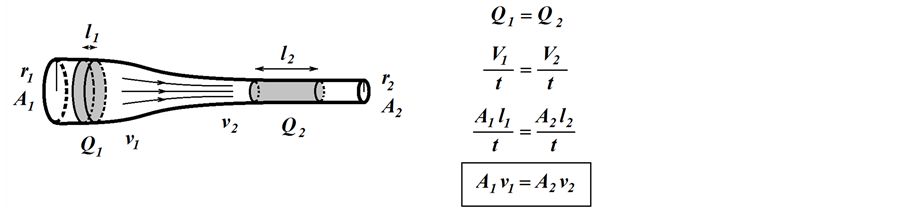
Şekil 1. Çapı ne olursa olsun bir borunun herhangi iki noktasında debi (Q) sabittir. Borunun kesit alanından (A) birim zamanda (t) geçen sıvının hacmi olarak tanımlanan debi formülü gizli olarak çap (r) ve akış hızı (v) parametrelerini içermektedir.
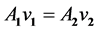 (1)
(1)
2.2. Bernoulli Yasası
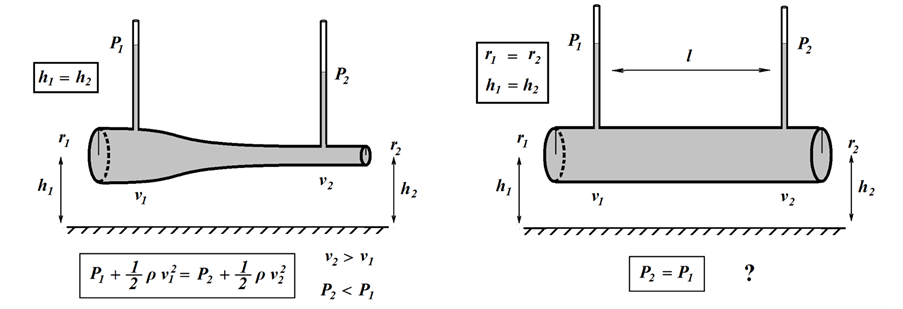
Akış borusu geometrisi, yükseklik farklılıkları, akışkanın basıncı ve akış hızı gibi parametreleri enerjinin korunumu prensibi çerçevesinde tartışan bu yasa, akışkanın iç sürtünmelerini göz önüne almaz. Bu koşulda, P basınç, ρ yoğunluk, g yerçekimi, h yükseklik, v akış hızı olmak üzere, akış borusunun farklı iki noktasında birim hacim akışkanın sahip olacağı toplam enerjilerin birbirine eşit olması beklenir (Equation (2)). Dolayısıyla Bernoulli yasası, toplam enerjinin bileşenleri olan basınç, potansiyel ve kinetik enerji terimlerinin birbiri arasındaki dönüşümlerini tartışmaktadır (Şekil 2(a)).
 (2)
(2)
Bernoulli yasasının, akış borusunun birbirinden farklı üç özel durumundaki çözümleri klinik olarak anlamlı değerlendirmeler yapılmasına neden olmaktadır.
1) İki nokta arasında yükseklik farkının olmadığı özel durum (h1 = h2): Damar çapının daraldığı noktada (r2) kan akış hızındaki (v2) artış kinetik enerji bileşeninde artışa neden olacaktır. Toplam enerjinin değişmezliği

(a) (c)
(b) (d)
Şekil 2. (a) Şekildeki gibi bir damarın herhangi bir noktasında birim hacimdeki akışkanın toplam enerjisi, P basınç, ρ yoğunluk, g yerçekimi, h yükseklik, v akış hızı olmak üzere basınç, potansiyel ve kinetik enerji terimlerinin toplamı kadardır. Akışkanın farklı iki noktada sahip olacağı enerji toplamları birbirine eşit ve sabittir; (b) İki nokta arasında yükseklik farkının olmadığı özel durum (h1 = h2); (c) İki nokta arasında çap farkının olmadığı özel durum (r1 = r2); (d) İki nokta arasında yükseklik ve çap farklarının olmadığı özel durum.
kuralı gereğince, bu noktadaki basınç enerjisinde (P2), kinetik enerjideki artış oranında azalma beklenmelidir (Şekil 2(b)). Basınç düşmesi, arter dallanma bölgelerinde yan dal kanlanmasında azalmaya neden olacağından, çıkan aortada koroner arter orifisleri cıvarında gözlenen böyle bir durumun fatal seyreden sonuçları söz konusu- dur.
2) İki nokta arasında çap farkının olmadığı özel durum (r1 = r2): Sadece yükseklik farklarının söz konusu olduğu bu durumda, Bernoulli yasası Pascal yasasına dönüşür (Şekil 2(c)). Bu yasaya göre, farklı yükseklikteki iki nokta (h1, h2) arasındaki basınç farkı (∆P) esas olarak yükseklik farkı (∆h= h2 − h1) tarafından belirlenir. Bu nedenle, kalp seviyesinden yukardaki bölgelerde kan basıncı daha düşük ölçülür.
3) İki nokta arasında yükseklik ve çap farklarının olmadığı özel durum: Bu özel durumda Bernoulli yasası, akış borusunun birbirinden uzak iki notasındaki birim hacim akışkanın sahip olacağı basınç enerjilerinin eşit (P1 = P2) olmasını gerektirmektedir (Şekil 2(d)). Ancak, geçerli olmadığı deneysel olarak gösterilen bu eşitlik, Bernoulli yasasının akışkanın viskozitesini (h) dikkate almamasından kaynaklanmaktadır. Viskozitenin de hesaba katıldığı durumda iki nokta arasında oluşan basınç farkı (∆P) Poiseuille yasası ile tanımlanmıştır.
2.3. Poiseuille Yasası
Şekil 2(d) deki gibi silindirik bir akış borusunda akan viskoz bir akışkanın, birbirinden “l” kadar uzakta iki noktası arasında oluşan basınç farkı (∆P), akışkanın iç sürtünmelerinin neden olduğu ısı enerjisine dönüşümü ile açıklanmaktadır. Sabit bir debiyle (Q) akışın sürdüğü durumda ısıya dönüşen enerjinin miktarı, Poiseuille tara- fından tanımlandığı gibi, akış direnci (R) ile doğru orantılıdır (Equation (3)). h viskozite, l akış borusunun boyu olmak üzere akış direnci ağırlıklı olarak yarıçap (r) tarafından belirlenmekte olup çapı yarıya düşüren bir daralma akışa gösterilen dirençte 16 kat artışa neden olacaktır (Equation (4)). Dolaşım sisteminde debi azal- masına neden olabilecek böyle bir durum, kalbin etkinliğini artırarak debideki kaybı telafi edecek miktarda ek bir basınç enerjisinin kana aktarılmasını gerektirecektir.
 (3)
(3)
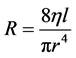 (4)
(4)
2.4. Viskozite Etkisi
Silindirik bir akış borusunda, iç içe tabakalardan oluştuğu varsayılan hipotetik viskoz bir akışkanın tabakaları, laminer akış koşullarında birbirine paralel seyretmektedir (Şekil 3(a)). Bu koşullarda tabakalar arasında oluşan akışa ters yöndeki sürtünme kuvvetleri (F) akışkanın viskozitesi (h) ile ilişkilidir (Şekil 3(c)). Viskozite, bu nedenle, laminer akış koşullarında akışkanın bizzat kendisinin akışa gösterdiği direngenliğin bir ifadesi olarak değerlendirilmektedir. Geometri kuralları gereğince, silindirik akış borusundaki viskoz akışkanın tabakaları arasındaki sürtünme yüzey alanları (S) çevreden merkeze doğru giderek azalmaktadır. Akış borusunun merke- zine doğru tabakalar arasında oluşan sürtünme kuvvetlerinde (F) de azalmaya neden olan bu durum, her bir
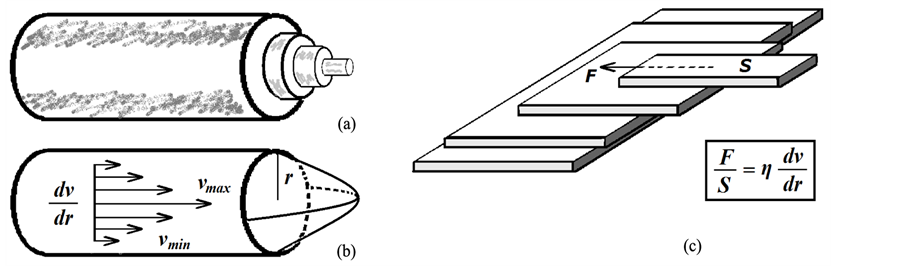
Şekil 3. (a) İç içe tabakalardan oluştuğu varsayılan hipotetik bir akışkanın akış sırasındaki şematik gösteri- mi; (b) Yarıçap (r) doğrultusundaki hız gradiyenti (dv/dr); (c) Dıştan içe silindirik tabakaların sürtünme yüzey alanları (S) ve tabakalar arasında oluşacak sürtünme kuvvetinin (F) değişimi.
tabakanın farklı bir akış hızına (v) sahip olması ile sonuçlanmaktadır. Akış hızında yarıçap doğrultusundaki bu değişim “hız gradiyenti” (shear rate, SR) olarak adlandırılmaktadır. Merkezdeki tabaka en yüksek hıza sahip olmak üzere, SR çevreden merkeze doğru parabolik bir değişim göstermektedir (Şekil 3(b)).
Genel olarak, akış yönüne ters yönde oluşan sürtünme kuvvetinin (F) yüzey alanına (S) oranı “kayma gerilimi” (shear stress, SS) olarak adlandırılır. Damar ile etkileşim halinde olan kanın en dış tabakası ile damar arasında oluşan SS, hemodinamik açıdan özel öneme sahip olup “duvar kayma gerilimi” (wall shear stress, WSS) olarak adlandırılmaktadır. Çalışmalar, endotel hücre davranışı üzerindeki doğrudan etkisi nedeniyle WSS’nin diğer hemodinami parametreleri kadar önemli olduğuna vurgu yapmaktadır [9] [10] .
SS’in, SR ve viskozite (h) ile arasındaki ilişki Newton viskozite yasası (Equation (5)) ile tanımlanmıştır [8] [11] .
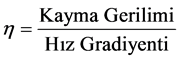 (5)
(5)
Bu yasaya uyan hava ve su gibi çoğu akışkanın viskozluk katsayısı sabittir ve “Newtoniyen” akışkan olarak değerlendirilir. Deneysel çalışmalar, kan gibi bazı akışkanların SS’indeki değişimler nedeniyle değişken bir viskoziteye sahip olabileceği ve bu nedenle de “Newtoniyen olmayan” akışkanlar adı altında başka bir grupta değerlendirilmesi gerektiğini göstermiştir [8] [12] . Ancak, aorta gibi büyük damarlarda viskozite etkisinin ihmal edilebilecek düzeyde olması nedeniyle, pratik amaçlarla çoğu hemodinami hesaplamalarında kan newtoniyen akışkan olarak kabul edilmektedir [8] [11] .
2.5. Laplace Yasası
Hemodinami açısından önemli olan bu yasa (Equation (6)), belirli bir “transmüral basınç” (Pt) etkisinde damar gibi esnek bir akış borusunun çeperinde oluşacak “gerilme kuvveti” (T) ve yarıçapı (r) arasındaki ilişkiyi tanımlamaktadır (Şekil 4).
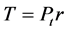 (6)
(6)
Yasaya göre, çapı büyük olan damar çeperlerinde daha büyük bir büyük bir gerilme kuvveti (T) oluşması, damar deformasyonları açısından büyük damarları daha riskli kılmaktadır. Bu da büyük yarıçaplı damar duvarının daha sağlam yapıda olmasının gerekçesini oluşturmaktadır [8] . Aksi durumda, aynı büyüklükteki gerilme kuvveti duvarı zayıflamış damar çapında daha fazla genişlemeye (dilatasyon) neden olarak transmural basıncı dengelemeye çalışacaktır.
SS ve gerilme kuvveti gibi damar duvarına doğrudan etkili kuvvetler, pulsatil kan akımının neden olduğu zamansal değişimlerin oluşturduğu kuvvetleri de içeren bir karaktere dönüşmektedir. Dolayısıyla, damar lümenini döşeyen endotel tabakası siklik ve transiyent karakterde statik olmayan karmaşık bir mekanik yük etkisinde kalmaktadır. Son zamanlarda, bu yükün aterogenez etiyolojisindeki olası etkisini araştıran çalışmalar dikkat çekmektedir [3] [13] . Bu çalışmalarda, hemodinamik kuvvetlerin damar endotel aktivitesinin düzenlen- mesinde, damar geometrisinin yeniden şekillenmesinde (anevrizma) ve ateroskleroz gelişiminde etkili olduğu bildirilmektedir [13] [14] .
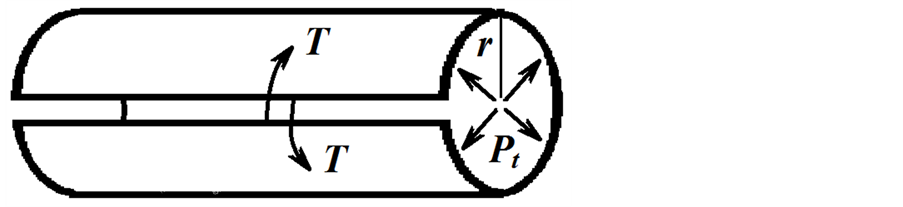
Şekil 4. Damar gibi silindirik (r) yarıçaplı esnek bir borudaki transmural basıncı (Pt) dengelemek için damar duvarında oluşan gerilme kuvveti (T). Gerilme kuvveti, damar boyunca açılan bir kesiğin uçlarını bir arada tuta- bilmek için, birim uzunluk başına uygulanması gerekli kuvvete karşılıktır. Pehlivan, F. den (8) değiştirilerek aktarılmıştır.
3. Tartışma
Deneysel fizyolojik çalışmalar, kan basıncı, gerilme kuvveti ve WSS gibi hemodinamik parametrelerin anevriz- ma gelişiminin, kan akış debisi ve akış hızı gibi gibi faktörlerin de aterosklerotik patolojilerin izlenmesindeki önemine vurgu yapmaktadır [15] [16] . Kan ile damar duvarı arasındaki etkileşimlerin uzaysal dağılımlarının yanı sıra pulsatil kan akımının bu etkileşim üzerindeki transiyent etkisinin de biliniyor olması klinik açıdan önem taşımaktadır. Bunun yanında, tedavi planlarının yapılması ve cerrahi ya da girişimsel tedavilerin olası sonuçları ile ilgili öngörülerin oluşturulması açısından da bu parametrelerin biliniyor olması önemlidir [10] [17] . Ancak, mevcut iv-vivo yöntemler ile başta SS olmak üzere, hemodinamik parametreleri ölçmek mümkün olmadığı gibi uzaysal ve zamansal dağılımları ile ilgili bilgi edinmek için de bu yöntemler yeterli değildir [15] . Bu nedenle, son zamanlarda hemodinamik parametrelerin hasta üzerinde doğrudan ölçülmesine yönelik minimal invazif yöntemler geliştirmesi yönünde multidsipliner bir motivasyon dikkat çekmektedir [5] [10] [17] .
Günümüz teknolojisi bu düzeyde yüksek çözünürlükte ölçüm yapılmasına uygun değildir. Ancak, klasik bir mühendislik uygulaması olan CFD, in-vivo ölçüme gerek duyulmaksızın, damarda tanımlanan her bir hacim elemanı için, ilgili parametrelerin hesaplanabildiği bilgisayar tabanlı bir araştırma yöntemi olarak tıbbi uygula- malar arasında yerini almış bulunmaktadır [4] - [7] . Özellikle aorta ve serebral arterlerde olduğu gibi, ciddi komplikasyonlarla seyreden damar darlıkları ve dilatasyonlarındaki gelişimin değerlendirilmesine yönelik klinik araştırmalar giderek artmaktadır [9] [10] . Gelecekte yaygınlaşması öngörülen “klinik tanı uzman sistemleri” hedefinin nüvesini oluşturduğuna inanılan bu araştırmaların, hastaya özel tedavi planı geliştirilmesi ve komp- likasyon risk değerlendirmesinde, yönlendirici sonuçları olacağı beklenmektedir.