Sand Waves Generation: A Numerical Investigation of the Infiernillo Channel in the Gulf of California ()
Received 21 April 2016; accepted 12 July 2016; published 15 July 2016

1. Introduction
Sand waves are rhythmic seabed features of great practical relevance. There are many economic activities interested in the presence and/or evolution of sand waves. Indeed, their migration can represent a serious hazard to pipelines that are +laid in regions of intense sea-bottom activity. Dredging may be required because sand waves migrate into or along shipping channels and harbors, hence reducing the local water depth and, consequently, affecting the navigability. It has been recognized that near-shore, migrating sand waves might even affect shoreline evolution and coastal defense works [1] . The presence of sand waves in some particular areas is strongly correlated to the amplitude of the spring tidal current [2] . One of the most striking characteristics of sand waves is that they are not static bed forms. They migrate with their crests almost orthogonal to the direction of the velocity oscillations induced by the tide, at a rate that strongly depends on the tidal characteristics that can reach some tens of meters per year [3] . Their shapes are often asymmetric but the steepness of the sides does not lead to flow separation [4] . Sand waves have spatial scales smaller than other bed-forms like sandbanks [5] . The wavelengths of sand waves are of some hundreds of meters, with amplitudes of several meters, and crests perpendicular to the principal tidal current axis [3] [6] . Tidal sand banks and sand wave fields can sometimes overlap, even with heights of the same order [7] .
As pointed out by Hulscher [4] , Gerkema [8] and other authors, the process that gives rise to the formation of sand waves is similar to originating dunes in rivers [9] or to that causing the appearance of sea ripples under sea waves [10] . The interaction of the oscillatory tidal current with a bottom perturbation gives rise to a steady streaming in the form of re-circulating cells. When the net displacement of the sediment dragged by this steady streaming steers toward the crests of the bottom waviness, the amplitude of the perturbation grows and bed- forms are generated. Hulscher [11] noted that the model of Huthnance [12] only predicts the formation of sand ridges, but no sand waves. She attributed it to the lack of a vertical structure of tidal currents. Hulscher [4] suggests that the vertical effect produced by a three dimensional model has to be included in order to generate sand waves. Contrary to the previous suggestion, our hypothesis is that sand waves may be generated and evolve even in the absence of vertical velocity gradients. Hence, the primary goal of this work was to test this hypothesis reproducing numerically sand waves by using a depth-integrated model coupled with a parameterized bedload sediment transport and a sediment conservation equation. In this investigation, we were able to reproduce successfully sand waves. Furthermore, we demonstrate that the presence of strong current horizontal velocity gradients associated with abrupt changes in the coastline alignment is critical in determining the sand-waves generation.
The Infiernillo Channel is a complex coastal wetland that includes reef, mangrove vegetation and coastal lagoons. Due to its high productivity, endemic characteristics, and fisheries, it has been also considered as a priority zone of conservation by the OEMGC (Marine Ecological System of the Gulf of California), as well as appropriate site to develop ecotourism activities. It is also a reserved fisheries area for the indigenous people by the government of Mexico [13] . There are some efforts to study the sand waves in this area: Merrifield et al. [14] carried out field surveys and observations of sand waves. Marzolf and Merrifield [15] made observations of tidal currents in the Infiernillo channel. In the present research work was carried out a numerical study on sand waves formation in the Infiernillo channel.
2. Study Area
The Infiernillo Channel is a narrow, shallow and long channel, averaging 7.6 km width that separates Tiburon Island from the Sonoran mainland (Figure 1). The averaged water depth of the channel is 5.5 m and its length is about 30 km. The adjacent areas to the channel are Agua Dulce, Sargento, Kunkaak and Kino Bays as well as the Tiburon Island. There are not continuous river inflows into the channel and only few alluvial flows into the sea. Surface water temperature fluctuates between 15˚C in winter and 30˚C in summer. The average salinity for Infiernillo Channel is 35‰, however salinities up to 40‰ have been recorded within the Channel in winter. Benthonic organisms cover large areas of the Infiernillo channel. These biological species are of ecological importance and of great economic value for the people who live around the area. The study of the sea bottom morphodynamics where these resources find their habitats and the relevance of the issue of coastal and biotic resources conservation is evident, hence the interest of this study.
Mixed tides characterize the study area. Most of Tiburón Island presents a rocky shoreline, however el Infiernillo Channel shows a sandy bottom and shoreline [16] . Merrifield et al. [14] describe sand waves and tidal
![]()
Figure 1. Geography (a) and topography (b) of the Infiernillo Channel, located in the Gulf of California. Agua Dulce and Kunkaak bays and Perla point are indicated. Satellite image obtained from U.S. Geological Survey. Landsat 5 TM, acquisition date 2011/10/12, color composite (3,2,1).
currents in the Infiernillo channel. Ebb currents flowing south from the channel form sand waves and tidal current ridges in Kunkaak Bay in water depths of less than 3 m. Surface ebb currents up to 1.7 knots, producing Froude Numbers of about 0.27 have been measured. The sand waves have wavelengths ranging from 12 m to 75 m and amplitudes from 0.30 m to 0.75 m. The sediment consists of well-sorted, coarse-grained sand; size-fre- quency distributions of the sediment samples are positively skewed.
In Agua Dulce Bay at the north end of the channel, sand waves developed in fine-grained sand. Size-fre- quency distributions of the sediment samples are negatively skewed. The sand on the crests is coarser in grain size and less negatively skewed than the sand in the troughs. The sand waves have wavelengths of 180 m to 250 m and amplitudes from 1.1 m to 1.5 m [14] . The sea-bottom of the Infiernillo channel consists of non-cohesive sediments, mainly sand forming shoals in the northern part of the channel as well as in the southern part. The shoals are one meter below the water surface and some of them emerge through the surface during the ebb at spring tides.
3. Methods
A two dimensional hydrodynamic-numerical model has been applied to simulate the depth average tidal currents in the Infiernillo channel, located in the archipelago region of the Gulf of California. Hence, the bedload sediment transport and the bottom morphodynamics were simulated for different geometrical configurations. Carbajal and Backhaus [17] , Montaño et al. [18] and Montaño-Ley et al. [19] [20] applied the model for different sea regions. It has been successfully applied to calculate the propagation of tidal waves in regions like the North Sea, the Gulf of California and the Topolobampo coastal lagoon, Mexico, among other sites. The model is based on the vertically integrated shallow water equations:
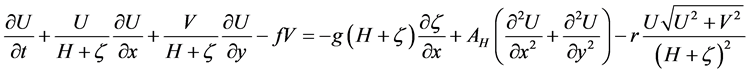 (1)
(1)
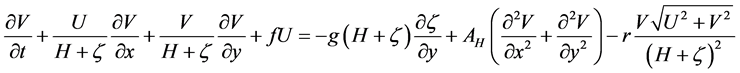 (2)
(2)
and the continuity equation
 (3)
(3)
x and y are the horizontal space variables, t is the time, U is the water transport (m2∙s−1) in the x direction, V is the water transport (m2∙s−1) in the y direction, 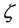 is the sea surface elevation (m);
is the sea surface elevation (m); 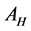 is the horizontal turbulent exchange coefficient (m2∙s−1),
is the horizontal turbulent exchange coefficient (m2∙s−1), 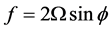 is the Coriolis parameter,
is the Coriolis parameter,  is the angular velocity of the earth,
is the angular velocity of the earth, 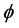 is the latitude (~29.25˚N in these calculations), H is the depth (m); g is the gravitational acceleration (m∙s−2); and r is the friction coefficient. The model was forced at the open boundaries with a sea surface elevation oscillation of the form
is the latitude (~29.25˚N in these calculations), H is the depth (m); g is the gravitational acceleration (m∙s−2); and r is the friction coefficient. The model was forced at the open boundaries with a sea surface elevation oscillation of the form
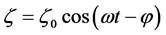 (4)
(4)
where 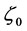 is the amplitude,
is the amplitude, 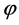 the phase and
the phase and 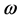 the frequency of the forcing wave, i.e. the frequency of the tidal constituent. To force the dynamics, tidal elevations and phases were prescribed at the two open boundaries, located in the northern and southern inlets, for the tidal harmonics K2, S2, M2, N2, K1, P1 and O1. The tidal harmonics were obtained from tidal simulations in the whole Gulf of California [17] and by interpolation of harmonics from Carbajal [21] . At the open boundaries, the gradient of the velocity was equal to zero.
the frequency of the forcing wave, i.e. the frequency of the tidal constituent. To force the dynamics, tidal elevations and phases were prescribed at the two open boundaries, located in the northern and southern inlets, for the tidal harmonics K2, S2, M2, N2, K1, P1 and O1. The tidal harmonics were obtained from tidal simulations in the whole Gulf of California [17] and by interpolation of harmonics from Carbajal [21] . At the open boundaries, the gradient of the velocity was equal to zero.
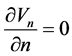 (5)
(5)
where 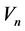 and n are the component of the velocity and space variable, respectively, normal to the open boundary. More details of the model can be seen in [21] .
and n are the component of the velocity and space variable, respectively, normal to the open boundary. More details of the model can be seen in [21] .
The applied bathymetry was obtained from Lancin [22] . The depth averaged tidal velocities predicted through the 2D hydrodynamic model were used to feed the sediment transport model. The parameterized bedload transport model applied in this investigation, has been given by Huthnance [12] , Hulsher et al. [11] , Schuttelaars and De Swart [23] , Van Rijn [24] , Montaño-Ley [25] , Montaño and Carbajal [26] and Carbajal and Montaño [27] [28] . The volumetric sediment flux Sb in the active layer, given by Van Rijn [24] is:
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
for some b > 1 and k* > 0. The term measured by the coefficient k* is a bed slope correction term which models the preferred downhill transport of sediment. Typical values for b and k* are b ≈ 3 and k* ≈ 2. The parameter s is a function of the sediment properties, ρs is the sediment density (2650 kg/m3) and d50 the mean sediment diameter. The value of s was calculated for d50 = 200 microns, according to the Equations (7) and (8) [24] [29] [30] . The water density is given by ρ and the critical velocity by ucr, i.e. the velocity value (~0.3 m∙s−1) to initiate the bed-load transport of sediment. The bed-load sediment transport components were obtained by using the velocity components and the bottom slope components in Equation (6).
The erosion-accretion patterns of sediments, i.e. the changes of the sea bottom, were determined by the sediment transport divergence:
![]() (9)
(9)
An important feature of this model is that the shape of the seabed is updated at every time interval and the current and sediment transport patterns are recomputed using the new bathymetry. A review of approaches to long term modeling of coastal morphology is given by De Vriend et al. [31] .
4. Results
The interaction between the tidal hydrodynamics and the sea bottom was investigated for the better understanding of the morphodynamics of coastal areas like the Infiernillo channel. In this research work, the morphodynamics in the Infiernillo channel has been investigated through several numerical experiments for different geometrical configurations, i.e. to investigate the influence of the coastal geometryon the sea-bottom morphodynamics. A depth integrated finite difference hydrodynamic model has been applied. The numerical experiments were performed in order to test the hypothesis that the geometry of a tidal basin has a profound effect on the sea-bottom morphodynamics, specifically on the sand wave generation.
This investigation consisted of three parts: firstly, different geometries with flat bottoms and unlimited sediment availability were exposed to oscillatory tidal currents in order to simulate the interaction of hydrodynamics and the bed-load sediment transport. It is important to mention that these geometries exemplify the dominant geographical features. Secondly a realistic coastal configuration of the Infiernillo Channel was used with the assumption of a flat sandy sea-bottom. In the third case, a real bathymetry and the actual configuration of the Infiernillo channel was applied in the numerical experiments.
The predicted depth averaged instantaneous tidal currents of the infiernillo channel has have been presented in Figure 2. Maxima predicted tidal current of about 0.7 m/s were predicted when the water flows into Kunkaak bay (t = 6 h), located in the southern part of the infiernillo channel. Figure 2 shows the vector fields for four different stages of the tides. Some areas presented convergence of the flow while others show flow divergence. Another feature of the velocities fields was the presence of a cyclonic eddy located right to the north of Pearl point (see Figure 1).
Figure 3 includes the morphodynamic of the sea bottom predicted for different geometries. The experiments started with a flat sandy sea bottoms and after 700 M2 tidal periods (approximately one year) the vertical changes were plotted. The assumption of flat bottom has been made in order to understand the effects of coastal geometry on the bottom morphodynamics. The maximum predicted vertical change was about 0.08 m. of accreted sediment while a minimum value of −0.08 m of eroded sediment was predicted for the elapsed time. It is worthwhile to note that bed-form patterns have been generated. The scales of these patterns corresponded quite well to the typical length scales of sand waves of 100 to 500 meters [4] (Figure 4(b)). The same order of
![]()
Figure 2. Tidal currents in the Infiernillo channel at different times.
![]()
Figure 3. Botttom morphology after one year of simulation for two different geometrical configurations representing the most important geographical features of the Infiernillo channel.
![]()
Figure 4. Comparison between observed (a) and calculated (b) sand waves in the Infiernillo channel. Satellite image obtained from U. S. Geological Survey. Landsat 5 TM, acquisition date 2011/10/12, color composite (3,2,1).
magnitude of the sand wavelengths were observed in satellite imagery of the Infiernillo channel (Figure 4(a)). It is also important to mention the presence of shoals located to the east of Perla point in Figure 4(a) and Figure 4(b). It is also worthwhile to note that the predicted sand waves and shoals in the considered coastal geometries were probably influenced by high velocity gradients or abrupt changes (90˚) in the coast alignment.
The second group of simulations includes a real coastal geometry of the Infiernillo channel but assuming a flat bottom (Figure 5). Under these conditions the vertical changes of the sea bottom were also computed after 700 M2 tidal periods. The results revealed the formation of tidal sand waves, shoals and probably sand banks. Once again, the sites where the sand waves were predicted coincide remarkably well with real sites where sand waves are observed in satellite imagery (see Figure 4). Figure 5 shows in detail sandwaves generated near Pearl point at the northern end of the Infiernillo channel. The incipient sand waves reveal wavelengths of about 250 meters. Around Perla Point there is a tendency to the formation of shoals with separation between crests of about 1 km. The most outstanding aspect to be mentioned is that sand waves are generated in the same area in all calculations, i.e. the fundamental features of a sea region determines where sand waves are generated.
Similarly, Figure 6 shows sandwaves evolving in the southern end of the infiernillo channel, i.e. in the Kunkaak bay. Another interesting aspect is the incipient rhythmic bed forms with distances between crests varying
![]()
Figure 5. Incipient sand waves and shoals in the northern part of the Infiernillo channel.
![]()
Figure 6. Calculated sand waves pattern in the southern part of the infiernillo channel (a). The konkaak bay area was taken from Figure 1(a). Dashed lines indicate the position of shoals. Satellite image obtained from U.S. Geological Survey. Landsat 5 TM, acquisition date 2011/10/12, color composite (3,2,1).
between about 1400 and 1800 meters. Satellite imagery also shows intense morphodynamics in the same area. The shoals which appear in the calculated pattern, showed in Figure 6(a), are also observed in the satellite image depicted in Figure 6(b) where the dashed lines indicate the position of the shoals. The comparison of calculated and observed shoals reveals a similar pattern.
The third group of numerical experiments were undertaken to simulate bedforms generation under realistic circumstances, i.e. a more accurate coastal geometry and bathymetry of the Infiernillo channel was applied in the calculations. Incipient wavy bed forms appear in different areas of the Infiernillo channel (Figure 7). Clearly, sand waves were generated near to Perla Point, in the central water body and in the southern part of the Infiernillo channel. These results agree with the previous calculations for more simple geometrical characteristics. The regions with intense morphodynamics are the same in all numerical simulations.
5. Discussion
A few decades ago, there was the perception that sand waves are generated by the vertical structure of tidal currents. Theoretical models, using vertically averaged velocities, could explain only the generation of sandbanks, i.e. bed forms with scales varying approximately between 2 and 14 km. The failure to explain the generation of sand waves was attributed to the lack of a vertical variation of tidal currents which is suppressed by the depth integration [11] . Later, it was demonstrated that with the consideration of a vertical variation of tidal currents, the theoretical model could predict the generation of bed forms with length scales similar to those of sand waves [4] . Several theoretical calculations of sand waves considered a vertical variation of the tidal flow [32] . Numerical models have also been able to simulate the sand wave generation [33] . Németh et al. [34] developed a two-dimensional numerical model describing vertical flow variations, morphological changes and the behavior of sand waves. They calculated a steady current situation induced by a wind stress applied at the sea surface. The bed forms found have wavelengths in the order of hundreds of meters when the resistance at the seabed is relatively large. The results also show that it is possible to model the initial evolution of sand waves with a numerical simulation model. They focus on sand waves in a unidirectional steady current with vertical variation.
The hypothesis that sand waves may be generated by depth averaged tidal currents and not necessarily by vertical velocity gradients has been tested. A crucial finding of this research work is then the fact that the geometry of a shallow water coastal areas and the presence of strong tidal currents (0.7 m/s) as well as abrupt changes in the coastline alignment were crucial in determining the generation of sand waves and other bed forms. It was possible to simulate the formation of sand waves applying a vertical integrated two-dimensional numerical
![]()
Figure 7. Calculated bed forms applying realistic geometrical conditions. accurate coastal and topographic information was used.
model. This model considers non-linear terms included in the equations of motion like the friction and the advection terms. These terms could represent the difference with respect to those results obtained in theoretical calculations. The reason for the generation of sand waves could be the non-linear interaction of Poincare waves produced by the interaction of tidal currents and the geometry of the Infiernillo channel [35] . It is important to mention that theoretical models, two or three-dimensional, consider an infinite ocean, i.e. no boundaries are contemplated. It represents a large difference with this 2D numerical model where a realistic interaction between tidal currents and a complex geometry is considered. Berthod and Pattiaratchi [36] studied the influence of the coastal geometry on rhythmic large-scale bed patterns. They applied a morphological model to an idealized headland situation. In the present investigation, sand waves and other bed forms were generated numerically at different locations in the main water bodies of the Infiernillo channel. The results of the numerical simulations agree with observations of sand waves made by Merrifield [14] near of Perlaspoint, in the northernmost part of the channel, and in the southern part where the Infiernillo channel widens into Kunkaak Bay. Other types of bedforms were also predicted in these numerical calculations. Shoals and sand banks were generated mainly in areas where the tidal flow interacts strongly with the geography (Figure 7). As far as we know, our investigation is the first work that simulates sand wave generation over an extensive sea bottom area applying complete vector fields velocities obtained from a 2D integrated model.
Particular features of bed forms in the Infiernillo channel have been observed. According to Merrifield [14] , sand bars were detected near to Agua Dulce Bay. In the same zone, sand waves with wave lengths between 200 and 270 m and amplitudes between 1.0 and 1.5 m were also documented. These sand waves developed in very fine sand conditions. Theoretical estimates indicate that the crests of the sand waves are oriented about 10˚ anticlockwise from the principal tidal flow [11] . Comparison between the tidal flow showed in Figure 2 and the crest pattern depicted in Figure 7 indicates that this property is reproduced adequately since crests and principal tidal flow are almost in the same direction. In Kunkaak bay, sand waves perpendicular to tidal currents were superimposed on much larger sand ridges. The calculated sand waves had wavelengths of approximately 75 m and amplitudes of about 0.32 m. In the present investigation sand waves were numerically predicted in both locations near Agua Dulce bay and in Kunkaak bay.
Figures 5-7 reveal the connection between the presence of sand waves and shoals and geographical features which resemblance headland and bays. It is worthwhile to notice that the predicted sand waves in all the coastal geometries were influenced by the presence of high velocity gradients associated with abrupt changes (90˚) in the coastline alignment (Figure 3). These bed patterns will probably evolve to more defined sandbanks or sand waves. Sand waves with typical length scales of the order of hundreds of meters are also observed.
Following the discussion on the bedform generation there are more evidences of the crucial effect of the coastal geometry effects. Applying a two-dimensional morphodynamic model for a tidal channel, Schramkowski et al. [37] showed that estuarine bars with typical length scales on the order of the tidal excursion length can be generated as the result of a positive feedback between water motion, sediment transport and the sandy bottom in a coastal configuration. Convergences and divergences of the tidally averaged sediment fluxes result in the evolution of the bed. The bottom morphodynamics of the infiernillo channel investigated through a 2D model show good qualitative agreement with the findings of Schramkowski et al. [37] . In The infiernillo channel the effects were the development of sand waves and sand banks. In agreement with Schramkowski et al. [37] , the bedform pattern is generated from flows that arise from tide and geometry interactions. Specifically, such flows always set up net sediment fluxes towards the formation of shoals and sand waves. In the present investigation we probe that coastal geometries particularly headlands and abrupt changes in the coastline orientation are associated to the generation of shoals and sand waves.
6. Conclusions
In the present investigation, sand wave and shoal patterns, resulting from the interaction of oscillatory tidal currents with the sea bottom have been predicted. The patterns were characterized by wavelengths comparable with those observed in the field or in satellite imagery.
We were able to reproduce sand waves. We also showed, through the application of a 2D depth integrated model, that sand waves are generated even in the absence of vertical velocity gradients. Sand waves formed near Perla point in the northern end of the Infiernillo Channel and in Kunkaakbay in the southern part while shoals and sand banks formed almost in the entire channel area.
The coastal geometry alignment turned out to play an important role in bedforms generation: Headlands and acute shifts in the shore alignment apparently trigger sand waves and sand bank formation. Convergence or divergence of tidal flow areas seems also to generate shoaling areas.
Another important result is that the calculated sand waves appear in the same area where they are observed in satellite imagery. The different numerical experiment yielded always the correct zone where sand waves exist. Since in these numerical experiments the main geographic properties were maintained, it is an indication that this aspect (where they occur) is determined by the coastal configuration.
Acknowledgements
Thanks to Victoria Montes-Montes for her assistance in this investigation and to the project: PAPIIT-UNAM IN-208673, for its support. We also thank to María de Jesús Guevara-Macías for her assistance in handling satellite imagery.