Radiative Effect on Flow and Heat Transfer over a Vertically Oscillating Porous Flat Plate Embedded in Porous Medium with Oscillating Surface Temperature ()
Received 2 March 2016; accepted 24 June 2016; published 27 June 2016
1. Introduction
The radiative free convective flow has many important applications in countless industrial and environment processes e.g. heating and cooling chambers, fossil fuel combustion energy processes, evaporation from large open water reservoirs, astrophysical flows, solar power technology and space vehicle re-entry. The radiative heat transfer plays an important role in manufacturing industries for the design of reliable equipment. Nuclear power plants, gas turbines and various propulsion devices for aircraft, missiles and satellites are examples of such engineering applications.
Magneto hydrodynamic free convection flow past an infinite vertical plate oscillating in its own plane was first studied by Soundalgekar [1] in case of an isothermal plate. Mansour [2] has studied the interaction of free convection with thermal radiation of the oscillatory flow past a vertical plate. Soundalgekar and Takhar [3] have considered radiation effects on free convection flow past a semi-infinite vertical plate. Helmy [4] has investigated MHD unsteady free convective flow past a vertical porous plate. Hossain et al. [5] have analyzed the heat transfer response of MHD free convective flow along a vertical plate to surface temperature oscillations. Radiation and free convection flow past a moving plate was considered by Raptis and Perdikis [6] . Hossain et al. [7] have described the effect of radiation on free convection from a porous vertical plate. Kim [8] has founded an unsteady MHD convective heat transfer past a semi-infinite vertical porous moving plate with variable suction. Radiation effects on the free convection over a vertical flat plate embedded in porous medium with high porosity have been studied by Hossain and Pop [9] . El-Arabawy [10] studied the effect of suction/injection on a micro polar fluid past a continuously moving plate in the presence of radiation. The effects of thermal radiation on the flow past an oscillating plate with variable temperature have been studied by Pathak et al. [11] . Chandrakala and Raj [12] have studied the effects of thermal radiation on the flow past a semi infinite vertical isothermal plate with uniform heat flux in the presence of transversely applied magnetic field. Das [13] has analyzed the exact solution of MHD free convection flow and mass transfer near a moving vertical plate in the presence of thermal radiation. Chandrakala [14] have studied the radiation effects on flow past an impulsively started vertical oscillating plate with uniform heat flux. Ibrahim and Makinde [15] have studied the radiation effect on chemically reacting MHD boundary layer flow of heat and mass transfer through a porous vertical flat plate. Radiation effect on natural convection near a vertical plate embedded in porous medium with ramped wall temperature has been studied by Das et al. [16] . Chandrakala [17] studied the effects of thermal radiation on the flow past an infinite vertical oscillating plate with uniform heat flux. Janaand Manna [18] studied the effects of radiation on unsteady MHD free convective flow past an oscillating vertical porous plate embedded in a porous medium with oscillatory heat flux. Vidyasagar and Ramana [19] studied the radiation effect on MHD free convection flow of Kuvshinshiki fluid with mass transfer past a vertical porous plate through porous medium. Radiation effects on mass transfer flow through a highly porous medium with heat generation and chemical reaction has studied by Mohammed Ibrahim [20] .
The aim of the present study is to investigate the radiative effect on flow and heat transfer over a vertically oscillating porous flat plate with oscillating surface temperature.
2. Formulation and Solution
2.1. Mathematical Model of Flow
To study free convective flow and heat transfer through a vertical porous flate plate in the influence of radiative heat flux is considered (Figure 1). The axis of x is taken along the vertical plate and the axis of y is normal to the plate.The plate is oscillating in its own plane with a frequency of oscillation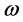 
and mean velocity
. The temperature at the plate is also oscillating and the free stream temperature is constant
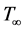. A constant suction velocity 
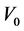is applied at the oscillating porous plate. Since the plate is of semi infinite length therefore the
variation along x-axis will be negligible as compared to the variation along y-axis so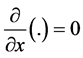 
In view of the physical description the governing equations are defined as follows:
The equation of continuity
![]()
reduces into
(1)
![]()
Figure 1. Physical model of the problem.
Þv, is independent of y and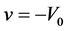 
(constant) is suction normal to the plate.
The momentum equation for the prescribed geometry is given by
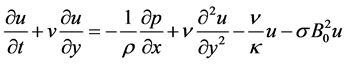(2)
Under usual Boussinesq’s approximation the Equation (2) becomes
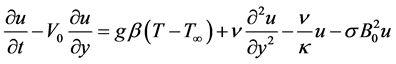(3)
The energy equation is given by
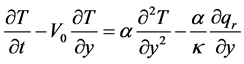(4)
The associated boundary conditions are
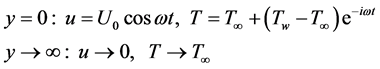(5)
where u the flow velocity component in the x-direction, ν the kinematic viscosity, g the acceleration due to gravity, β the volumetric expansion coefficient, α the thermal diffusivity,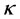 
the thermal conductivity, 
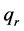the radiative heat flux, T the fluid temperature, ![]()
the ambient temperature and ![]()
the amplitude of oscillation of the plate.
The Roseland approximation for radiative heat flux [Brewster, 1992] is given by
![]()
where σ is Stefan ? Boltzmann constant and ![]()
is the mean absorption coefficient.
Taking the Taylor series expansion of T4 and neglecting terms with higher powers, we have
![]()
2.2. Mathematical Formulation
Introducing following dimensionless quantities
![]()
Equations (3), (4) and the associated boundary conditions (5) reduces into
![]()
(6)
![]()
(7)
where, ![]()
is suction parameter, ![]()
the Grashof number, M the magnetic parameter, Da the Darcy number, R the radiative parameter, ![]()
the Prandtl number, and ![]()
The corresponding boundary conditions are
![]()
(8)
There is no loss of generality in omitting the asterisk from (6) to (8).
2.3. Numerical Solution
To solve the coupled nonlinear partial differential Equation (6) and (7) along with the boundary conditions (8), the solution for u and ![]()
(after dropping *) the following form will be suitable
![]()
(9)
![]()
(10)
where![]()
, ![]()
, ![]()
and ![]()
are unknown to be determined.
Invoking the Equations (9) and (10) in the Equations (6) and (7) and equating harmonic and non harmonic terms, the set of ordinary differential equations are given as
![]()
(11)
![]()
(12)
![]()
(13)
![]()
(14)
where, primes denote derivative with respect to y
The corresponding boundary conditions are
![]()
(15)
![]()
(16)
The Equations (13) and (14) are ordinary differential equations with prescribed boundary conditions as given in (15) and (16), therefore their solutions are straight forward are given by
![]()
(17)
![]()
(18)
where ![]()
Now using expression of ![]()
and ![]()
in the Equations (11) and (12) we get second order ordinary differential equations in ![]()
and ![]()
given by
![]()
(19)
![]()
(20)
In view of the boundary conditions associated with ![]()
and![]()
, the solution of the Equations (19) and (20) are known and given by
![]()
(21)
![]()
(22)
where![]()
, ![]()
and ![]()
are constant quantities.
Now substituting expression of![]()
, ![]()
, ![]()
and ![]()
in the Equations (9) and (10)
![]()
(23)
![]()
(24)
3. Skin Friction
The skin-friction at the plate, which in the non-dimensional form is given by
![]()
(25)
and computed values are given in Table 1.
4. Nusselt Number
The non dimensional coefficient of heat transfer defined by Nusselt number is obtained and given by
![]()
(26)
and computed values are given in Table 2.
5. Results and Discussion
The velocity profiles for different parameter like Suction parameter, Grashof number, magnetic parameter, Darcy number, Prandtl number and radiation parameter are shown by Figures 2-7. Temperature profiles are also shown by Figures 8-10. In Figure 2, the positive values of S correspond to cooling of the plate decreases in the vicinity of the permeable plate while increases in region close to non permeable wall. In Figure 3, the positive values of Gr correspond to cooling of the plate increases in the vicinity of the permeable plate while decreases in region close to non permeable wall. In Figure 4 when magnetic parameter M is increased, keeping other parameters constant the velocity increases. In Figure 5 when Darcy number Da is increased, keeping other parameters constant the velocity decreases. In Figure 6 and Figure 7 when Prandtl number Pr and radiation parameter
![]()
Table 1. Non dimensional coefficient of Skin Friction-Cf.
![]()
Table 2. Non dimensional coefficient of Heat Transfer- Nu.
![]()
Figure 2. Variation in velocity with suction parameter at Gr = 5, M = 5, Da = 0.1, Pr = 1, R = 2,![]()
.
![]()
Figure 3. Variation in velocity with Grashof number at S = 0.5, M = 5, Da = 0.1, Pr = 1, R = 2,![]()
.
![]()
Figure 4. Variation in velocity with magnetic parameter at S = 0.5, Gr = 5, Da = 0.1, Pr = 1, R = 2,![]()
.
![]()
Figure 5. Variation in velocity with Darcy number at S = 0.5, Gr = 5, M = 5, Pr = 1, R = 2,![]()
.
![]()
Figure 6. Variation in velocity with Prandtl number at S = 0.5, Gr = 5, M = 5, Da = 0.1, R = 2,![]()
.
![]()
Figure 7. Variation in velocity with radiation parameter at S = 0.5, Gr = 5, M = 5, Da = 0.1, Pr = 1,![]()
.
![]()
Figure 8. Variation in temperature with suction parameter at Pr = 1, R = 2,![]()
.
![]()
Figure 9. Variation in temperature with Prandtl number Pr at S = 0.5, R = 2,![]()
.
![]()
Figure 10. Variation in temperature with radiation parameter at S = 0.5, Pr = 1,![]()
.
R is increased, velocity increases in the vicinity of the permeable plate while decreases in region close to non permeable wall. In Figure 8, the positive values of S correspond to cooling of the plate increases temperature decreases and the negative values of S correspond to heating of the plate decreases temperature increases. Figure 9 and Figure 10 represent that temperature decreases when Prandtl number and radiation parameter R increases. The variation in fluid velocity and temperature in the porous medium through the one period of oscillation is demonstrated by Figure 11 & Figure 12. The fluid velocity and temperature oscillates up to a certain distance from the plate while this oscillation diminishes at large distance from the plate.
Table 1 represents the values of skin friction. The positive values of S correspond to cooling of the plate increases skin friction increases and the negative values of S correspond to heating of the plate decreases skin friction decreases. The positive values of Gr correspond to cooling of the plate increases skin friction increases and the negative values of Gr correspond to heating of the plate decreases skin friction decreases. When M is increased the skin friction increases and when Da is increased skin friction decreased. When Pr and R is increased the skin friction increases.
The values of Nusselt number is given in Table 2. The positive values of S correspond to cooling of the plate increases Nusselt number increases and the negative values of S correspond to heating of the plate decreases Nusselt number decreases. When R and Pr are increased the Nusselt number decreases.
6. Conclusions
・ Fluid flow slows down in the vicinity of the permeable plate while enhances in region close to nonpermeable
![]()
Figure 11. Variation in velocity with ![]()
and distance from the plate at S = 0.5, Gr = 5, M = 5, Da = 0.1, Pr = 1, R = 2.
![]()
Figure 12. Variation in temperature with ![]()
and distance from the plate at S = 0.5, Pr = 1, R = 2.
wall on increasing suction parameter correspond to cooling of the plate.
・ Fluid velocity profiles increase in the vicinity of the permeable plate while decrease in region close to non permeable wall with the increase in Grashof number correspond to cooling of the plate
・ Fluid velocity profiles increase in the vicinity of the permeable plate while decrease in region close to non permeable wall when Prandtl number and radiation parameter is increased.
・ Fluid velocity and temperature in the porous medium through the one period of oscillation oscillates up to a certain distance from the plate and this oscillation disappears far away from the plate.
・ The values of skin friction increase when magnetic parameter, Prandtl number and radiation parameter are increased while the values of skin friction decrease when Darcy number is increased.
・ Nusselt number decreases when Prandtl number and radiation parameter are increased.