Received 20 April 2016; accepted 21 June 2016; published 24 June 2016

1. Introduction
The following statements were written in the paper “Time Dilation and Length Contraction Shown in Three- Dimensional Space-Time Frames” published in Concepts of Physics, Vol. VI, No. 2, 2009. “Since the concept of the movement phenomenon of an object is more fundamental than the concepts of space and time, its unit of velocity is more fundamental than the units of space (length) and time, which are derivations. Furthermore, without gravitational force, we would be unable to measure the gravitational mass of an object; without spring force, we would be unable to measure the inertial mass of an object. Since the concept of the force phenomenon applied to an object is more fundamental than the concept of mass, the unit of force is more fundamental that the unit of mass, which is also a derivation.”
In this paper, we like to have a further discussion about this issue. In order to measure something, we need to define a unit of measurement. In this way, all measurements are multiples or fractions of that unit. The units of measurement are defined as standard. The International System of Units (SI) defined seven fundamental units of measure based on conventional and historical reasons from which all other SI units are derived [1] . For this paper, the topic is limited to mechanics. These SI fundamental units are commonly called metric units. The definitions of fundamental units are based on physical objects such as standard second clocks, standard meter sticks and standard kilogram bars. A day is divided in 24 hours, each hour divided in 60 minutes, each minute divided in 60 seconds. A second clock is equal to 1⁄(24 × 60 × 60) of the day. A meter stick is equal to 1⁄10,000,000 of the distance from the Earth’s equator to the North Pole measured on the circumference through Paris. A kilogram bar is equal to the mass of one liter of water. A liter is one thousandth of a cubic meter. In classical physics, time and length are absolute and independent, so fundamental units match with fundamental quantities. In modern physics, time and length are relative and dependent; thus fundamental units are not equivalent to fundamental quantities.
2. Special Relativity
Einstein placed two guns at the middle of the train with moving velocity u, he fired a pair of photons from these two gun at the same time on Figure 1. The length of a car of the train is 2d.
Light has a duality including wave and photon. The velocity of light is the limit velocity of particles in the universe. The velocity of light, 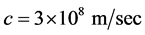 which is the fixed value measured by any observers, no matter which direction of photons are fired.
which is the fixed value measured by any observers, no matter which direction of photons are fired.
1) For observers on the train:
The velocities of both photons are same. The time of a photon hitting the front wall is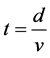 . The time of photon hitting the back wall is
. The time of photon hitting the back wall is 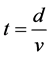 . Therefore, observers on the train will see the two photons hits both
. Therefore, observers on the train will see the two photons hits both
the front wall and back wall simultaneously.
2) For the observers on the platform:
The time for the photon hitting the front wall is 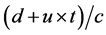 which is longer. The time for the photon hitting the back wall is
which is longer. The time for the photon hitting the back wall is 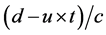 which is shorter. This shows that one photon will hit the back wall earlier than the front wall. Thus, these two events are not happening simultaneously.
which is shorter. This shows that one photon will hit the back wall earlier than the front wall. Thus, these two events are not happening simultaneously.
Classical physics shows that two events happen simultaneously are absolute, so space and time are independent. Einstein’s thought experiment shows that two events happening simultaneously are relative, so space and time are dependent.
Now, let’s modify Einstein’s thought experiment by firing a photon from the floor to the ceiling on Figure 2.
The platform with S frame, the train with S’ frame, and the train travels to the right with velocity u. Observers on the train see a photon moving from the floor to the ceiling vertically and the track of motion is h. Observers on the platform see a photon moving from the floor to the ceiling slantingly and the track of motion is r. The distance of train traveled from the time a photon leaving the floor to the time reaching the ceiling is x. Three lengths r, x, h form the right triangle, and we can derive the formula
![]()
Figure 1. Einstein’s famous thought experiment: A pair of photons are fired at middle of the train.
![]()
Figure 2. Modified Einstein’s thought experiment by firing a photon from the floor to the ceiling. The sides r, x, h of a triangle form the right triangle.
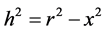
from the Pythagorean theorem. Replacing h by ct', r by ct, and x by ut and by simplifying the equation, we derive the time contraction formula [2]
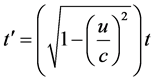 .
.
For example, the velocity of the train measured by observers on the platform is u = 0.6c, and the train traveled 25 sec. When we input these data into the time contraction formula measured on the train, we get
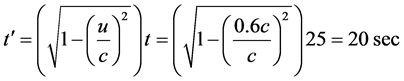
measured on the train which is shorter then t = 25 sec. Special Relativity shows that the time that light moves from the floor to the ceiling are not absolute. Because there are two different possible values of 25 sec or 20 sec for the same event, time cannot be treated as a fundamental quantity.
From the time contraction formula of

multiplying u on the equation of both sides, we get the formula of

ut' is the distance traveled by the train measured from observers on the train denoted by x', ut is the distance traveled by the train measured from observers on the platform denoted by x on Figure 3. The length contraction formula can be expressed as
 .
.
Using the formulas, the velocity of the train is u = 0.6c and travels 25 sec measured by the observers on the platform. The distance traveled by the train is 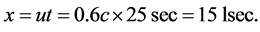 Input these data into the formula of length contraction, then we can calculate the distance traveled by the train measured from the train is
Input these data into the formula of length contraction, then we can calculate the distance traveled by the train measured from the train is
![]()
This result is the same as the result from another formula
![]()
Figure 3. Modified Einstein’s thought experiment by shooting a photon from the floor to the ceiling. The distance, x, traveled by the train is measured from the platform.
![]()
It is shorter than x = 15 lsec. Special Relativity shows that the length (distance) of the train travels from the photon leaving the floor to reach the ceiling is not absolute. Because there are two different possible values of 15 lsec or 12 lsec for the same travel event, so length cannot be treated as a fundamental quantity.
3. Construct a New Space-Time Frame
In The Trouble with Physics, the author mentions that: “Descartes and Galileo made a most wonderful discovery. In this way, time is represented as if it were another dimension of space. This ‘spatialization’ of time is useful but may be challenged as representing a static and unchanging world” [3] .
We construct a new space-time frame by presenting time using polar coordinates.
If the unit of time is sec, then the unit of radius for polar circle is chosen to be light second (lsec), then the unit of x-axis should be chosen as light second (lsec) on Figure 4. We construct this new space-time frame to make space and time dependent by using the unit of lsec.
If the unit of time is year, then the unit of radius for polar circle is chosen to be light year (lyr), then the unit of x-axis should be chosen to be light year (lyr) on Figure 5. We construct this new space-time frame to make space and time dependent by using the unit of lyr.
The advantage of this coordinate frame is that line OA not only represents the motion of the train observed from the platform, but also represents the tract of the photon traveling observed from the platform on Figure 6. From the figure on the new space-time frame, it shows that ![]() because OO'A is right triangle. We are able to derive time contraction formula
because OO'A is right triangle. We are able to derive time contraction formula
![]()
and length contraction formula
![]()
replacing OA by ct, OO' by ut, and O'A by ct' which were discussed on the previous section [4] .
The advantage is that the O'B can represent the motion of the platform, and O'A can represent the motion of the train from observer’s perspective on Figure 7. The point B and the point A are on the same circle with the radius of ct'. In order to find the direction of the line O'B, we should find the value of O'Q which is equal to x'. From these polar coordinate frames, the triangle O'BQ is proved to be similar to the triangle OAO' because
the value of the fraction of ![]() multiplied by t on the numerator and denominator is the same value as
multiplied by t on the numerator and denominator is the same value as ![]() mul tiplied by t'. Therefore
mul tiplied by t'. Therefore ![]() →
→![]() . As long as x, r, r' are given, x' can be calculated.
. As long as x, r, r' are given, x' can be calculated.
![]()
Figure 4. Construct a new space-time frame by presenting time with unit of l sec using polar coordinates.
![]()
Figure 5. Construct a new space-time frame by presenting time with unit of lyr using polar coordinates.
The ratios of distance to time are proved to be same for both frames. From the previous result ![]() →
→![]() →
→![]() →
→![]() . The velocity of train traveling measured from observers on the platform is
. The velocity of train traveling measured from observers on the platform is
same as the velocity of platform measured from observers on the train. It shows that the traveling train and the platform are a pair of inertial frames [5] .
In order to describe the motion of an object in 3-dimensional space along the locations of x-axis, y-axis, and z-axis, we can construct a new space-time frame. Spheres with different radius representing different outgoing time, polar coordinates will be formed from circles of intersections between spheres and x-y plane, y-z plane,
![]()
Figure 6. Red circles represent the polar coordinates on the platform. We are able to construct a new space-time frame by presenting time with polar coordinates on the platform to describe the motion of the train using the line OA.
![]()
Figure 7. Blue circles represent the polar coordinate on the train. We are able to construct a new space-time frame by presenting time with polar coordinate on the train to describe the motion of the platform using the line O'B.
and z-x plane on Figure 8. We are able to use the red polar coordinates of x-y plane, the blue polar coordinates of y-z plane, and the gray polar coordinates of z-x plane to describe the locations of a moving object moving along x-axis, y-axis, and z-axis [6] . This kind of new coordinate frame embedding time axis into space axes is called three-dimensional space-time frame which saves one dimension. We won’t be puzzled by being not able to visualize four-dimensional space-time frame.
4. Fundamental Units International System (SI) of Units
The General Conference on Weights and Measures has replaced all but one of the definitions of its fundamental
![]()
Figure 8. Three-dimensional space-time frame formed by three polar planes on three different planes.
units based on physical objects (such as standard time clocks, standard meter sticks, or standard kilogram bars) with physical descriptions of the units based on stable properties of the Universe. SI fundamental units are current (2005) formal definition [1] .
The meter is the length of the path traveled by light in vacuum during a time interval of 1/299,792,458 of a second. From d = ct and c = 299,792,485 m/sec in order to travel 1 meter distance, then the time taken by light is![]() . We use the velocity of light to define the unit of length 1 meter (1 m).
. We use the velocity of light to define the unit of length 1 meter (1 m).
The second is the duration of 9,192,631,770 cycles of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom. From the wave property of light,
![]() , then
, then ![]() or
or ![]() The light is emitted by a caesium atom, its frequency is 9,192,631,770
The light is emitted by a caesium atom, its frequency is 9,192,631,770
cycles/sec. ![]() then
then![]() .
.
We use velocity of light ![]() to define the unit of time, 1 second.
to define the unit of time, 1 second.
These physical definitions allow scientists to reconstruct meter standards or standard clocks anywhere in the world, or even on other planets, without referring to a physical object kept in a vault somewhere.
In fact, the kilogram is the only fundamental unit still defined by a physical object. The International Bureau of Weights and Measures (BIPM) keeps the world’s standard kilogram in Paris, and all other weight standards, such as those of Britain and the United States, are weighed against this standard kilogram.
My opinion, about that the definition of kilogram defined by BIPM, is that they still use gravitational con-
stant, G, as a hidden value, through the action of weighting![]() , where
, where ![]() (M is the
(M is the
mass of the earth, R is the distance from the scale to the center of the earth) is exactly same value for both mass on the scale at the same location. Under the balance of the scale, the weight of the standard mass on left side is equal to the weight of the prototype mass on the right side of scale. We can conclude that the standard mass is equal to the prototype mass. Without gravitational force, we are not able to check the balance of the standard mass with the prototype mass.
5. Conclusions
If we want to understand time and space, we cannot study them separately. It is our misconception to believe that time and space own innate properties. Actually without movement, we are not able to measure the elapsed time or the distance of traveled. The movement of an object helps us better understand the concept of time and space.
Since the concept of movement is more fundamental than the concept of space and time, then choosing the velocity of light as a fundamental quantity is reasonable. Since we are able to measure the mass of an object through gravitational force, then choosing force as a fundamental quantity is reasonable.
Because of the constant velocity of light, we should treat velocity of light as fundamental quantity and time and length become derived quantities. In the International System of Units, the velocity of light is already used to define 1 sec and 1 meter, and gravitational force is also used to define 1 kg of mass by balancing with the prototype on scale. In modern physics, we should treat physical events as fundamental elements of thoughts instead of individual objects.
Here we have summarize the discussion in the conclusion of Contextual Principle: We are able to cognize the being of an individual through the existence of phenomena and are able to describe the properties of that individual through the individual’s possession of contextual attributes. We are not able to cognize the being of an individual through the existence of individual itself and are not able to describe the properties of that individual through the individual’s possession of innate attributes. Physical events are much fundamental than individual objects.