Uniform Persistence, Periodicity and Extinction in a Delayed Biological System with Stage Structure and Density-Dependent Juvenile Birth Rate ()
Received 20 May 2016; accepted 17 June 2016; published 20 June 2016

1. Introduction
In the natural world, there are many species whose individual members have a life history that takes them through two stages: juvenile and adult. Individuals in each stage are identical in biological characteristics, and some vital rates (rates of survival, development and recruitment) of individuals in a population almost always depend on stage structure [1] - [3] . Thus, we need to consider stage structure in population problems accordingly. In recent years, some authors ( [1] - [18] ) studied the stage-structured predator-prey systems. The authors of [2] - [11] have studied the stability or Hopf bifurcation of these type systems. Since environmental and biological parameters (such as the seasonal effects of weather, food supplies, mating habits, hunting or harvesting season, etc.) fluctuate naturally over time, the authors of [12] - [18] have explored a class of nonautonomous biological systems with stage structure. Recently, Yang et al. considered the following predator-prey system with stage structure for prey [18] :
 (1.1)
(1.1)
All the coefficients in system (1.1) are continuous positive  periodic functions. Sufficient and necessary conditions are obtained for the permanence of the system.
periodic functions. Sufficient and necessary conditions are obtained for the permanence of the system.
Sometimes, the past state as well as current conditions can influence biological dynamics and such interactions have motivated the introduction of time delay in stage-structured predator-prey systems [2] - [5] [8] - [13] . Time delay due to gestation is the time interval between the moments when an individual prey is killed and when the corresponding biomass is added to the predator population. That is to say, the reproduction of predator after predating the prey is not instantaneous but will be mediated by some discrete time lag required for gestation of predator. The authors of [8] - [10] have studied a class of stage-structured predator-prey models with time delay due to gestation of predator.
In some stage-structured populations, the intraspecific and interspecific competitions occur within each stage structure. And each stage-structured density affects not only its population but also other stage-structured populations. In two-stage single-species population, Abrams and Quince have demonstrated that adult population competition makes a low birth rate of juvenile population [19] . Adult population has to compete for resources to reproduce when population size or density is larger. Correspondingly, juvenile population birth rate is a function of adults’ density and remains bounded when adults’ size is large due to limited resources [20] . This density- dependent regulator has been found in beetles, tribolium, copepods, scorpions, several fish species and even crows by Polis [21] .
Motivated by the above facts and based on the recent work of Yang et al. [18] , we consider the following stage-structured predator-prey model:
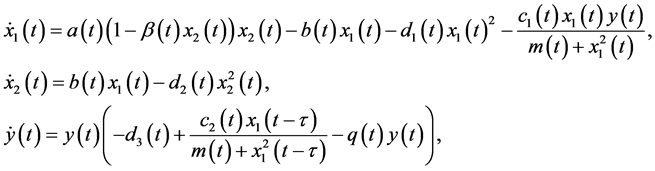 (1.2)
(1.2)
where ,
,  and
and  represent the density of immature prey, mature prey and predator species, respectively. The coefficients in system (1.2) are all continuous positive T periodic functions in which
represent the density of immature prey, mature prey and predator species, respectively. The coefficients in system (1.2) are all continuous positive T periodic functions in which 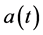 represents the maximum per capita birth rate into the immature prey,
represents the maximum per capita birth rate into the immature prey, 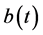 is the recruitment rate of immature prey becoming mature prey,
is the recruitment rate of immature prey becoming mature prey,  is the death rate of the immature prey population, and
is the death rate of the immature prey population, and  is death rate of the mature prey population. The parameter
is death rate of the mature prey population. The parameter  is the proportional rate of decrease in per capita births with increased mature prey density and takes a value between 0 and 1 [19] , which can be considered as density de-
is the proportional rate of decrease in per capita births with increased mature prey density and takes a value between 0 and 1 [19] , which can be considered as density de-
pendent coefficient. The function  represents the Holling type-IV functional re-
represents the Holling type-IV functional re-
sponse of the predator to the immature prey and 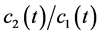 is the conversion rate of nutrients into the reproduction of the predator. The parameter
is the conversion rate of nutrients into the reproduction of the predator. The parameter  is the delay due to gestation, that is, only the mature adult predator can contribute to the production of predator biomass. The parameters
is the delay due to gestation, that is, only the mature adult predator can contribute to the production of predator biomass. The parameters  and
and ![]() denote the death rate and the overcrowding rate of the predator population, respectively.
denote the death rate and the overcrowding rate of the predator population, respectively.
The initial conditions for system (1.2) take the form of
![]() (1.3)
(1.3)
where![]() , the Banach space of continuous functions mapping the interval
, the Banach space of continuous functions mapping the interval
![]() into
into![]() , where we define
, where we define ![]() and the interior of
and the interior of ![]() as
as
![]() .
.
At the same time, we adopt the following notations through this paper:
![]() (1.4)
(1.4)
where ![]() is a continuous T-periodic function.
is a continuous T-periodic function.
The remainder of this paper is organized as follows. In Section 2, we introduce some lemmas and then explore the uniformly persistence and periodicity of system (1.2). In Section 3, we investigate the extinction of the predator population in system (1.2). In Section 4, numerical simulations are presented to illustrate the feasibility of our main results. Conclusion is given in Section 5.
2. Uniform Persistence and Periodicity
In this section, we analyze the uniform persistence and periodicity of system (1.2) with initial conditions (1.3). First, we introduce the following definition and lemmas, which are useful for obtaining our results.
Definition 2.1. The system![]() ,
, ![]() is said to be uniformly persistent if there are constants
is said to be uniformly persistent if there are constants
![]() such that every positive solution of this system satisfies
such that every positive solution of this system satisfies![]() .
.
Definition 2.2. The system![]() ,
, ![]() is said to be weakly uniformly persistent if there are
is said to be weakly uniformly persistent if there are
constants ![]() such that every positive solution of this system satisfies
such that every positive solution of this system satisfies![]() .
.
Lemma 2.1. (See [22] ). If ![]() and
and ![]() are all continuous T periodic functions for all
are all continuous T periodic functions for all![]() , and
, and![]() ,
, ![]() then the system
then the system
![]() , (2.1)
, (2.1)
has a unique positive T periodic solution which is globally asymptotically stable.
Lemma 2.2. (See [23] ). If![]() ,
, ![]() ,
, ![]() and
and ![]() are all positive and continuous T periodic functions for all
are all positive and continuous T periodic functions for all![]() , then the system
, then the system
![]() (2.2)
(2.2)
has a positive T periodic solution ![]() which is globally asymptotically stable with respect to
which is globally asymptotically stable with respect to
![]() .
.
Theorem 2.1. System (1.2) is uniformly persistent and has at least one positive T periodic solution provided that
![]() , (2.3)
, (2.3)
where ![]() is the unique positive periodic solution of system (2.2) given by Lemma 2.2.
is the unique positive periodic solution of system (2.2) given by Lemma 2.2.
We need the following propositions to prove Theorem 2.1.
Proposition 2.1. There exists a positive constant ![]() and
and ![]() such that
such that
![]()
Proof. Obviously, ![]() is a positively invariant set of system (1.2). Given any solution
is a positively invariant set of system (1.2). Given any solution ![]() of system (1.2) with initial conditions (1.3), we have
of system (1.2) with initial conditions (1.3), we have
![]() ,
,
![]() .
.
Consider the following auxiliary system:
![]() (2.4)
(2.4)
By Lemma 2.2, system (2.4) has a unique globally attractive positive T periodic solution![]() . Let
. Let ![]() be the solution of system (2.4) with
be the solution of system (2.4) with![]() . By the vector comparison theorem [24] , we have
. By the vector comparison theorem [24] , we have
![]() (2.5)
(2.5)
From the global attractivity of![]() , for any positive constant
, for any positive constant ![]() (
(![]() ), there exists a T1 > 0, such that for all
), there exists a T1 > 0, such that for all ![]()
![]() (2.6)
(2.6)
By applying (2.5) and (2.6), we obtain![]() ,
, ![]() ,
,![]() . Let
. Let![]() , we have
, we have![]() . In addition, from the third equation of (1.2) we have
. In addition, from the third equation of (1.2) we have
![]() ,
,
for all![]() . Consider the following auxiliary equation:
. Consider the following auxiliary equation:
![]() (2.7)
(2.7)
By Lemma (2.1), we obtain that system (2.7) has a unique positive T periodic solution ![]() which is globally asymptotically stable. Similarly to the above analysis, for the above
which is globally asymptotically stable. Similarly to the above analysis, for the above![]() , there exists a
, there exists a![]() , such that
, such that
![]() (2.8)
(2.8)
Set![]() , then
, then![]() .
.
Proposition 2.2. There exists a positive constant![]() , such that
, such that
![]()
Proof. By Proposition 2.1, there exists a positive ![]() such that
such that![]() ,
,![]() .Hence, from the first and second equations of system (1.2), we obtain
.Hence, from the first and second equations of system (1.2), we obtain
![]()
![]() ,
,
for![]() . By Lemma 2.2, the following auxiliary system
. By Lemma 2.2, the following auxiliary system
![]() (2.9)
(2.9)
has a unique global attractive positive T periodic solution![]() . Let
. Let ![]() be the solution of system (2.9) with
be the solution of system (2.9) with![]() , by the vector comparison theorem, we obtain
, by the vector comparison theorem, we obtain
![]() (2.10)
(2.10)
Moreover, from the global attractivity of![]() , there exists a
, there exists a![]() , such that
, such that
![]() (2.11)
(2.11)
Combined (2.10) with (2.11), we have
![]()
Therefore, ![]() ,
,![]() .
.
Proposition 2.3. Suppose that (2.3) holds, then there exists a positive constant![]() , such that any solution
, such that any solution ![]() of system (1.2) with initial conditions (1.3) satisfies
of system (1.2) with initial conditions (1.3) satisfies
![]() (2.12)
(2.12)
Proof. By assumption (2.3), we can choose arbitrarily small constant ![]() (without loss generality, we as-
(without loss generality, we as-
sume that![]() , where
, where ![]() is the unique positive periodic solution of sys-
is the unique positive periodic solution of sys-
tem (2.2)), such that
![]() , (2.13)
, (2.13)
where![]() . Consider the following system with a parameter
. Consider the following system with a parameter![]() ,
,
![]() (2.14)
(2.14)
By Lemma 2.2, system (2.14) has a unique positive T periodic solution![]() , which is globally
, which is globally
attractive. Let ![]() be the solution (2.14) with initial condition
be the solution (2.14) with initial condition![]() . Then, for the above
. Then, for the above![]() , there exists a sufficiently large
, there exists a sufficiently large ![]() such that
such that![]() , for
, for![]() ,
,
![]() . Using the continuity of the solution in the parameter, we have
. Using the continuity of the solution in the parameter, we have ![]() uniformly in
uniformly in
![]() as
as![]() . Hence, there exists a
. Hence, there exists a ![]() such that
such that![]() , for
, for![]() ,
, ![]() ,
,![]() . So, we get
. So, we get ![]() Choosing a
Choosing a
constant ![]() (
(![]() ,
,![]() ), we obtain
), we obtain
![]() (2.15)
(2.15)
Suppose that the conclusion (2.12) is not true, then there exists ![]() such that
such that
![]() , (2.16)
, (2.16)
where ![]() is the solution of system (1.2) with initial condition
is the solution of system (1.2) with initial condition
![]() ,
,![]() . So, there exists
. So, there exists ![]() such that
such that
![]() , (2.17)
, (2.17)
for![]() . Then, from the first and second equation of system (1.2), we have
. Then, from the first and second equation of system (1.2), we have
![]() (2.18)
(2.18)
for all![]() . Let
. Let ![]() be the solution of system (2.14) with
be the solution of system (2.14) with ![]() and
and
![]() , then we have
, then we have
![]()
By the global asymptotic stability of![]() , for the given
, for the given![]() , there exists
, there exists![]() , such that
, such that
![]()
So, ![]() ,
, ![]() ,
,![]() . By using (2.15), we obtain
. By using (2.15), we obtain
![]() (2.19)
(2.19)
Therefore, by using (2.17) and (2.19), for ![]() it follows:
it follows:
![]() (2.20)
(2.20)
Integrating (2.20) from ![]() to t yields
to t yields
![]() .
.
Thus, from (2.13) we know that ![]() as
as![]() , which is a contradiction. The proof is complete. □
, which is a contradiction. The proof is complete. □
Proof of Theorem 2.1. By Propositions2.2 and 2.3, system (1.2) is uniform weakly uniformly persistent. From Propositions 2.1 and Theorem 1.3.3 in [25] , system (1.2) is uniformly persistent. Using result given by Xu, Chaplain and Davidson in [26] or Wang and Zhu in [27] , we obtain system (1.2) has at least one positive T periodic solution. This completes the proof of Theorem 2.1.
3. Extinction
In this section, we investigate the extinction of the predator population in system (1.2) with initial conditions (1.3) under some condition.
Theorem 3.1. In system (1.2), suppose that
![]() , (3.1)
, (3.1)
where ![]() is the unique positive periodic solution of system (2.2) given by Lemma 2.2, then
is the unique positive periodic solution of system (2.2) given by Lemma 2.2, then
![]() .
.
Proof. According to (3.1), for every given positive constant ![]()
![]() , there exists
, there exists ![]()
![]() and
and ![]() such that
such that
![]() . (3.2)
. (3.2)
From the first and second equations of system (1.2), we have
![]() ,
,
![]() ,
,
Hence, for the above ![]() there exists a
there exists a![]() , such that
, such that
![]() (3.3)
(3.3)
It follows from (3.2) and (3.3), that for![]() ,
,
![]() . (3.4)
. (3.4)
First, we show that exists a![]() , such that
, such that![]() . Otherwise, by (3.4), we have
. Otherwise, by (3.4), we have
![]()
as![]() .
.
That is to say![]() . This is a contradiction. Second, we show that
. This is a contradiction. Second, we show that
![]() (3.5)
(3.5)
where ![]() is bounded for
is bounded for![]() . Otherwise, there exists a
. Otherwise, there exists a![]() , such that
, such that![]() . By the continuity of
. By the continuity of![]() , there must exist a
, there must exist a
![]() such that
such that ![]() and
and ![]() for
for![]() . Let
. Let ![]() be the nonnegative integer such that
be the nonnegative integer such that![]() . According to (3.3), we have
. According to (3.3), we have
![]()
which is a contradiction. This shows that (3.5) holds. By the arbitrariness of![]() , it follows immediately that
, it follows immediately that ![]() as
as![]() . This completes the proof of Theorem 3.1.
. This completes the proof of Theorem 3.1.
From Theorem 2.1 and 3.1, we obtain that the density dependent coefficient ![]() has no influence on permanence and extinction of system 1.2. But, from the following simulation, we can know the density dependent coefficient has effect on the populations’ densities of system (1.2).
has no influence on permanence and extinction of system 1.2. But, from the following simulation, we can know the density dependent coefficient has effect on the populations’ densities of system (1.2).
4. Examples
In this section, we provide some examples to illustrate the feasibility of our main results in Theorems 2.1 and 3.1 and then explore the effect of density dependent coefficient![]() .
.
Example 4.1. Let
![]() (4.1)
(4.1)
In this case, system (2.2) given by Lemma 2.2 has a unique positive periodic solution
![]() . Furthermore, by a simple calculation, we have
. Furthermore, by a simple calculation, we have
![]() .
.
Let![]() , according to Theorem 2.1, system (1.2) with the above coefficients is uniformly persistent and admits at least one positive 2π-periodic solution. Figure 1 shows the dynamic behavior of system (1.2).
, according to Theorem 2.1, system (1.2) with the above coefficients is uniformly persistent and admits at least one positive 2π-periodic solution. Figure 1 shows the dynamic behavior of system (1.2).
Let![]() , according to Theorem 2.1, system (1.2) with the above coefficients is uniformly persistent and admits at least one positive 2π-periodic solution. Figure 2 shows the dynamic behavior of system (1.2).
, according to Theorem 2.1, system (1.2) with the above coefficients is uniformly persistent and admits at least one positive 2π-periodic solution. Figure 2 shows the dynamic behavior of system (1.2).
From Theorem 2.1, we know that the density dependent coefficient ![]() has no influence on the uniform persistence of system (1.2). However, from Figure 1 and Figure 2, we can see that the density dependent coefficient
has no influence on the uniform persistence of system (1.2). However, from Figure 1 and Figure 2, we can see that the density dependent coefficient ![]() affects the populations’ densities of system (1.2). Figure 1 demonstrates that the system have high densities with the low density dependent coefficient; whereas Figure 2 shows the system have low densities with the high density dependent coefficient.
affects the populations’ densities of system (1.2). Figure 1 demonstrates that the system have high densities with the low density dependent coefficient; whereas Figure 2 shows the system have low densities with the high density dependent coefficient.
Example 4.2. Let
![]() (4.2)
(4.2)
In this case, by a simple calculation, we obtain![]() . According
. According
to Theorem 3.1, system (1.2) is impermanent and the predator population experiences extinction. The numerical simulation shown in Figure 3 also confirms this result.
5. Conclusion
In this paper, we propose a stage-structured predator-prey system with time delay and density-dependent juve-
nile growth. We explore the uniformly persistent and extinction of system (1.2). By Lemma 2.2, we know that ![]() is the globally attractive periodic solution of system (1.1) without density dependence and predation. Hence, condition (2.3) implies that system (1.2) is uniformly persistent if the death rate of the predator population is sufficiently small. Numerical simulations not only show the consistency with the theoretical analysis but also exhibit other interesting biological phenomenon. Form Figure 1, Figure 2, we know that although the density dependent coefficient has no influence on the permanence of system (1.2), it affects the system populations’ densities.
is the globally attractive periodic solution of system (1.1) without density dependence and predation. Hence, condition (2.3) implies that system (1.2) is uniformly persistent if the death rate of the predator population is sufficiently small. Numerical simulations not only show the consistency with the theoretical analysis but also exhibit other interesting biological phenomenon. Form Figure 1, Figure 2, we know that although the density dependent coefficient has no influence on the permanence of system (1.2), it affects the system populations’ densities.
Funding
This work was supported by the National Natural Science Foundation of China (No. 31370381), the General Project of Educational Commission in Sichuan Province (Grant No. 16ZB0357), the Major Project of Educational Commission in Sichuan Province (Grant No.16ZA0357) and the Major Project of Sichuan University of Arts and Science (Grant No.2014Z005Z).
NOTES
![]()
*Corresponding author.