A Biomechanical Model of Human Lung Deformation Utilizing Patient-Specific Elastic Property ()
Received 26 March 2016; accepted 17 June 2016; published 20 June 2016

1. Introduction
Accurate prediction of respiratory lung deformation is crucial for tumor localization and targeted radiotherapy in patients with lung cancer [1] . Respiration-induced tumor motion constitutes a potential source of error in tumor localization for optimum radiotherapy [1] . Specifically, it can lead to an under-treatment of the tumor and overexposure of the surrounding healthy tissues to unnecessary ionizing radiation. Image-based methods have been used extensively for quantification of such lung motion [1] . However, imaging methods do not account for the physiological properties of the lung. Biomechanical models have recently become popular for representation of lung motion. These models often rely on simplified property data derived from animal studies [2] - [4] . In addition, the accuracy of such models has not been systematically assessed. The present study applies a biomechanical model utilizing human subject-specific lung properties and assesses model accuracy by comparison of prediction with those derived from image registration.
The spatio-temporal lung deformation is predicted in patients with lung cancer undergoing radiation therapy. The simulation is performed on three-dimensional (3D) lung geometries reconstructed from 4DCT scan dataset of two human patients. The numerical simulation utilizes a porous flow-structure interaction technique to simultaneously solve the coupled airflow equations and structural dynamics of the lung tissue.
Four-dimensional computed tomography (4DCT) registration and dynamic magnetic resonance imaging has been widely used for identification of the lung and tumor movements [5] [6] . Although imaged-based methods provide direct means to obtain the displacement, they are limited by the lack of breathing physiology and physical properties of the lung. Biomechanical modeling that enables simulation of physics and physiology-based lung deformation has therefore been generating interest of recent.
Biomechanical modeling to predict lung deformation has been studied extensively to complement imaging [7] [8] . Numerical modeling of lung deformation is however challenging due to structural complexity, heterogeneity of lung parenchyma, boundary conditions and subject-specific breathing pattern [9] . A number of studies have considered the lung as linearly elastic [10] [11] and nonlinear hyper-elastic [12] [13] , with the lung generally considered as a one-phase continuum [14] [15] . Al-Mahya et al. [16] assessed the effect of type of computational elements, linear material properties, and geometry on the modeling of lung motion. It was found that the displacement was minimally affected by these factors with 95 percentile of displacement differences ranging between 0.4 and 0.8 mm. However, the time required for the analyses increased from 3.4 min for linear element with linear geometry, to 95 mins for quadratic elements with nonlinear geometry. Therefore, linear tetrahedral elements coupled with linear elastic materials and linear geometry was considered superior for modeling the breathing-induced lung motion for radiotherapy applications.
In spite of the growing number of studies on the dynamics of human lung, a systematic validation of modelling results with imaging data acquired directly from real patients has not been undertaken. This deficiency is addressed here through direct validation of predicted lung deformation using the results of image registration. Image registration has been demonstrated to accurately represent lung motion based on 4DCT imaging of patients with lung cancer [18] [19] . Thus 4DCT scan datasets are used here to validate results of our biomechanical modelling of lung deformation.
The biomechanical model uses the geometry and spatially-dependent elastic properties obtained for two specific patients. Heterogeneity of lung parenchyma is particularly important for cancerous lungs in which tumor can significantly increase local stiffness [10] [17] [18] . Image analysis has also shown that larger lung tumors affect local lung dynamics and deformation patterns [19] - [21] . It should be remarked that this study does not consider tumor directly. However our methodology is applicable to lungs with and without tumor since it involves acquisition of data for the spatial material properties over the lung parenchyma with or without tumor.
The paper is divided into five sections of which this Introduction is the first. Section 2 presents the materials and methodology employed. This section first describes the image registration method used to provide the geometry, elastic data and displacement data derived from image registration. Next, the biomechanical model is described including the acquisition of the material property utilized, boundary conditions imposed and the mathematical formulation of the fluid-structure interaction phenomenon. Computational details are described in Section 3, followed by Section 4 in which the modelling predicted results are presented and verified with the imaging data. The last Section 5 discusses the results and summarizes the major implications of the findings.
2. Materials and Methods
This section describes the method used to estimate lung deformation from integration of image registration and numerical simulation using finite element model. A schematic of the integrated approach is presented in Figure 1 indicating the various steps involved in the determination of the image-based and model-based displacements. It also includes the inverse approach used to acquire the material properties, as well as the methodology for implementation in the finite element numerical model.
![]()
Figure 1. Processing pipeline diagram illustrating various steps involved in the determination of the image- based and model-based displacements.
2.1. Image Registration
The 4DCT scans used were acquired from in vivo experiments on two human male adult patients at different stages of the breathing cycle. The 4DCT datasets at 10% tidal volume intervals were acquired using Siemens Biograph strain-gauge 64 slices CT. The 3D volumetric lung were segmented using Pinnacle MBS and OSIRIX software. A 4DCTdata registration algorithm was used to estimate the motion of each 3D voxel at end-expira- tion 3D volume data by searching for and locating a corresponding voxel in another 3D volume at a different breathing phase.
An optical flow-based motion estimation method was used for the registration [22] . The method is based on local Taylor series approximation. One of the limitations of the method as applied to estimating 3D organ motion is the low sensitivity to variations in regional motion. To improve accuracy, a multi-level, multi-resolution method [23] was used, which computed optical flow between two 3D volumes at lower resolution, propagated the result to the higher resolution volume, and subsequently to the original resolution volume data. In this approach, the organ anatomy was divided into four parts: 1) lung outline, 2) large capillaries, 3) small capillaries, and 4) parenchyma region (Santhanam et al., 2011). At each level of anatomy, a multilevel, multi-resolution optical flow registration was used for computing the 4D organ motion of that anatomy and integrated into the next level. The accuracy of the 4D image registration protocol was assessed by placing a set of 100 landmarks inside the lung and tracking them from the end-inspiration volume to the end-expiration volume. Our results indicate that the accuracy is ~2 mm and is sub-voxel in nature. The 4DCT images had no visible artifacts as they were acquired using a well calibrated 5D imaging protocol [24] . The displacement data from 4DCT registration were obtained with the same coordinates as the geometry and material data. The images had slice increment of 1.0 mm in the superior-inferior (SI) direction.
2.2. Biomechanical Modeling
2.2.1. Overview
Human lung has a complex structure . On the macro scale the lung parenchyma can be modeled as a saturated porous medium with the thin-walled tissue structure as the solid phase and air in the alveoli and ducts as the fluid phase. Considering this sponge-like nature enables us to model the anatomic complexity of the lung parenchyma in a computationally cost-effective manner. Thus, the lung is considered a poro-elastic medium where fluid and solid domains coexist and share space. Although the airways are not segmented separately the presence of large airways and ducts as well as blood vessels is represented as local in homogeneity.
2.2.2. Solid Structure
Most soft tissues under loading exhibit nonlinear stress-strain relationship, which involves the application of finite elasticity [16] . However, linear elasticity has been extensively assumed and used for modeling of soft tissue behavior because of its simplicity. In the context of radiotherapy, Al-Mayah et al. [16] have shown that the simple linear material model is sufficient for simulating lung deformation as an alternative to the hyper-elastic model. Their study on 14 lung cancer patients show that for a patient that experiences the largest diaphragm motion, most of the deformation is concentrated in the lower lobes of the lungs and dissipates rapidly within a short distance from the diaphragm-lung interface. A similar behavior has been observed in a comprehensive study on 152 lung cancer patients [25] . Therefore it was concluded that even if a large deformation is applied to the lung, most of the lung actually experiences little deformation. This finding implies that linear isotopic material properties can provide results comparable to nonlinear anisotropic material properties. We have thus assumed that the lung tissue is linear isotropic elastic in the present study. Our results show that this assumption is quite sufficient for most of the lung except near the diaphragm. It should be noted that the above assumption represents a compromise between complexity and computational cost. Besides, the effect of any error caused by this assumption can be compensated for by the dominant effect of diaphragm pressure.
An inverse non-invasive methodology is used to estimate the elastic properties of the 3D volumetric lung [18] . Basically, the lung is decomposed into voxel points and a correlation is defined to estimate the deformation operator of each voxel point for known values of the applied force and the displacement during breathing. The values of airflow and volumetric displacement are used as input to estimate the deformation operator in terms of Green’s function (GF). A heterogeneous GF based formulation is considered for both the surface and volumetric deformation. The structural and functional constants estimated for the surface lung dynamics are also used for the volumetric dynamics. The GF for the volumetric lung is reformulated in the spectral domain using Hyper- Spherical Harmonic (HSH) transformation, which is the 3D extension of Spherical Harmonic (SH). Upon simplification, the HSH coefficients of the displacement (d) are represented as a product of the HSH coefficients of the applied force and the deformation operator thus:
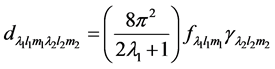 (1)
(1)
where  and
and 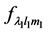 represent the value of displacement and applied force respectively, which are represented by their HSH coefficients. The deformation operator can be estimated from Equation (1) in terms of
represent the value of displacement and applied force respectively, which are represented by their HSH coefficients. The deformation operator can be estimated from Equation (1) in terms of
their spherical harmonic coefficients. The term 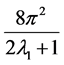 refers to the normalization factor of the SO(3) rotation group.
refers to the normalization factor of the SO(3) rotation group.
The applied force is computed using pulmonary function test [26] which provides the pressure corresponding to the various lung volumes during breathing. The volumetric lung displacement is estimated using 4DCT registration as described in Section 2.1. Each voxel point is then associated with a single Young’s modulus and a common Poisson’s ratio of 0.35. The average values of Young’s modulus obtained for the two patients used for this study were 1 kPa (Patient 1) and 5 kPa (Patient 2). Figure 2 illustrates the 3D volume-rendering representation of the Young’s modulus obtained for the two patients.
2.2.3. Fluid Domain
The flow is assumed unsteady and laminar. The fluid is assumed to be Newtonian and incompressible with density ρf = 1.205 kg∙m−3 and viscosity μf = 1.83 × 10−5 kg∙m−1∙s−1.
![]()
Figure 2. Three-dimensional volume rendering of the Young’s modulus values for (a) Patient 1, (b) Patient 2.
2.2.4. Porous Fluid-Structure Interaction
The Arbitrary Lagrange-Euler (ALE) formulation is applied to the fluid domain since it is deformable. The pore fluid flows through the porous solid structure according to the Darcy’s law [27] , thus:
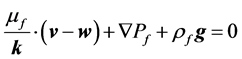 (2)
(2)
where k, μf and ρf represent the permeability tensor, viscosity and density of air respectively, v is the air velocity vector, w is the moving mesh velocity vector, Pf is the pore pressure and g is the gravity vector. In this study the 4DCT scans are acquired when the patient lies in the supine body position during radiotherapy. Therefore our calculation assumes this supine body position and gravity is applied in the posterior direction. In the coupled porous media, the porosity and permeability are defined as [27] :
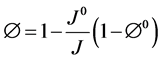 (3)
(3)
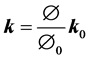 (4)
(4)
where J is the geometric element Jacobian and the superscript “0” indicates the quantities at initial reference configuration. In the current model the reference state is considered to be at the end of exhalation when the lung is at rest.
A Lagrangian formulation is used for the solid domain. The lung tissue is assumed to be linear elastic and isotropic [25] . Note that isotropic assumption is considered only at the elemental level and the Young’s modulus is allowed to change from one element to another. Allowance is made for geometric nonlinearities by assuming the deformation to be large. Unlike the conventional FSI approach in which the fluid and structural variables are coupled only at the interface, in the porous fluid-structure interaction (PFSI) approach they are coupled in the whole porous medium through displacement and traction conditions [27] . The microscopic fluid stress is added to the structural model as an internal stress. The stresses in the porous medium are thus expressed as:
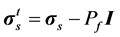 (5)
(5)
where Pf and 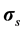 represent respectively the pressure of the pore fluid and Cauchy stress tensors of the skeleton,
represent respectively the pressure of the pore fluid and Cauchy stress tensors of the skeleton, 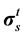 is the total Cauchy stress in the solid model and I is the identity matrix.
is the total Cauchy stress in the solid model and I is the identity matrix.
The total Cauchy stress tensor in the solid model is transformed to the second Piola-Kirchhoff. The governing equation for the total stress in the solid model is the momentum equation given by:
 (6)
(6)
where us represents the displacement vector in the solid domain and ρs represents the density of the tissue. 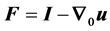 is the deformation gradient tensor,
is the deformation gradient tensor, 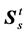 is the total second Piola-Kirchhoff stress tensor in the porous medium and b is body force. Displacement is interpreted to be an estimate of the lung motion field during breathing, from end of expiration to end of inhalation. The compatibility of displacement/velocity must be satisfied in the whole porous medium , thus;
is the total second Piola-Kirchhoff stress tensor in the porous medium and b is body force. Displacement is interpreted to be an estimate of the lung motion field during breathing, from end of expiration to end of inhalation. The compatibility of displacement/velocity must be satisfied in the whole porous medium , thus;
![]()
![]() (7)
(7)
where uf is the fluid displacement and ΩP represents the porous domain. This condition also ensures that the moving mesh velocity in a previous Equation (2) is identical to the solid velocity (![]() ) in the porous medium. The above equations are solved in ADINA [28] commercial code subject to the boundary conditions described below.
) in the porous medium. The above equations are solved in ADINA [28] commercial code subject to the boundary conditions described below.
2.2.5. Boundary Conditions
Normal respiration involves a process often termed negative pressure breathing. During each breath changes in the intrapleural pressure acts upon the lung surface and establishes a sub-ambient pressure within the lungs. The pressure applied on lung for a given change in volume is computed using the pressure-volume curve measurement [26] . Here, periodic pressure boundary condition is assumed on the lung surface over the breathing cycle as shown in Figure 3. In a normal breathing process, air flow is generated by the pressure applied to the tissue. Thus, for realistic simulation of breathing mechanics a stress-free boundary condition is specified at the flow inlet to the lung assumed to be at the hilium. The lung is anchored both at the top and at hilium to be consistent with the imaging experimental results.
3. Computational Details
The 3D lung geometry is first reconstructed from the 4DCT dataset of patients using the Mimics commercial code [29] and used to construct the computational grid by means of 3-matic commercial code [30] . A 4-node tetrahedral and a 3-node triangular element are used respectively for volume and surface discretization. Both solid and the fluid geometries are comprised of the whole volume of the lung and are similarly meshed.
The fluid and the solid equations are solved by the iterative two-way coupling or partitioned method embodied in ADINA computational code [31] . In this approach, the fluid and solid equations are solved independently in sequence, using the most recent information from another part of the coupled system. This iteration is continued until convergence is reached in the solution of the coupled equations. A mesh-independence study is performed to ensure numerical accuracy. The final meshes chosen from the mesh-independence test and used for the computations are summarized in Table 1.
4. Results
Figure 4(a) and Figure 4(b) show the predicted map of the absolute displacement (in mm) at the end of inspiration for Patients 1 and 2, respectively. The maximum and minimum displacements are shown with variations between the two extremes. The figures show that the absolute displacement generally increases from the interior to the outer surface and from the top to the bottom of the lung. This trend is consistent with the distribution of the intrapleural pressure that originates from the ribcage and diaphragm and gradually attenuates towards the top and interior parts of the lobe. However, the local displacement pattern depends on the shape of the lung and the distribution of the elastic properties. In addition, Patient 1 has a larger absolute displacement than Patient 2 due primarily to the difference in breathing pattern and Young’s modulus. Specifically, the maximum pressure
![]()
Figure 3. Prescribed boundary pressure profile.
![]()
Figure 4. Predicted amplitude map of displacement magnitude in (mm) at the end of inhalation for (a) Patient 1, (b) Patient 2.
![]()
Table 1. Number of computational elements and nodes used in the biomechanical model.
boundary condition is 100 Pa for Patient 1 and 40 Pa for Patient 2 with the corresponding average Young’s modulus of 1 kPa and 5 kPa, respectively.
In order to check the accuracy of the model, the left and right lungs of each patient are divided into four regions at the midpoint in the superior-inferior (SI) and left-right (LR) directions as shown in Figure 5. Fifty landmarks are selected in each region and the absolute average error and standard deviation in the LR, anterior- posterior (AP), and SI directions are plotted for each region as shown in Figure 5. The predicted error typically ranges from 0.73 mm to 3.6 mm in the left lung and 0.72 mm to 3.2 mm in the right lung for Patient 1. The corresponding values for Patient 2 are 0.41 mm to 2.9 for left lung and 0.32 mm to 2.8 mm for right lung. The displacement error is generally larger in the outer region (near ribcage) than the inner regions of the lungs. This result indicates that representation of the contact between the lung and chest wall will need further improvement in future study. The predicted displacement at the bottom-interior parts of the right lungs (R3) is more accurate than the bottom-interior parts of the left lungs (L3). The accuracy of the results are clearly affected in the regions near the heart as the amplitude of lung displacement induced by cardiac motion has not been considered in the present model. Although it is desirable to improve the underlying assumptions of the model, it is noteworthy that the predicted average error over most of the lung is within 3 mm which is considered clinically acceptable [31] .
In order to compare the accuracy of the heterogeneous and homogeneous models, 50 landmarks are selected at the bifurcation of the airway where the effect of heterogeneity of the lung tissue is expected to be significant. The average YM values are used for the reference cases utilizing homogenous property. Table 2 summarizes the mean absolute errors and the standard deviation of the selected landmarks in the AP, LR, and SI directions for each patient. The errors are significantly lower with the heterogeneous than the homogeneous model in all cases. In particular, the reduction in the SI direction ranges from 3.2 mm to 1.03 mm for Patient 1, and 1.8 mm to 0.78 mm for Patient 2.
The transient displacement of 18 selected landmark locations in the lung are also monitored and compared for both the biomechanical model and image registration data. The location of the selected landmarks as well as their transient displacement profiles over the inhalation phase are plotted in the Figure 6 and Figure 7. The landmarks were selected in the periphery of the lung (one near the ribcage and the other near the interior surface), and the third in the core region. The results obtained from the two methods are generally in good agreement.
Figure 6(a) shows that the FE result is favorably matched with the imaging results at locations P1 and P2. However, the discrepancy is larger for P3 which is located near the ribcage.
In Figure 6(b), landmark P6 which is located near the ribcage exhibits the largest discrepancy between the two sets of results, similar to location P3 in Figure 6(a). However, P4 which is located near the heart on the interior surface of the lung has larger discrepancy than its corresponding node, P1 in Figure 6(a).
The absolute displacements for the landmarks at the bottom as presented in Figure 6 care generally higher than those in previous Figure 6(a) and Figure 6(b) located at the top and the middle of the lung. In Figure 6(c), again the largest discrepancy is observed for the monitored locations near the heart (P7) and ribcage (P9).
The transient displacement profiles for the landmarks in the right lung are shown in Figures 7(a)-(c), at the top, middle, and bottom of the lung, respectively. The trends of displacement profiles are generally similar to those already presented above for the left lung. Specifically, the absolute displacement increases from top to bottom. The locations near the rib cage also exhibit similar behavior to those observed in the left lung, with larger errors at these locations than the interior surface and core of the lung.
5. Conclusions
A biomechanical model has been developed and applied to model spatial lung deformation and validated with data obtained from 4DCT registration on two human patients. The average local error and standard deviation in each direction are used as metrics to assess the accuracy of the model. The regional difference in the prediction error is also investigated. The regions near the ribcage and heart exhibit relatively larger displacement errors than the interior of the lungs. The transient absolute displacement obtained from imaging and biomechanical modeling are monitored and compared at 18 locations for both left and right lungs. The discrepancy between the methods is generally less than 3 millimeters, for most of the interior of the lung which is considered acceptable for radiotherapy. Specifically, the lung radiotherapy literature indicates that a 3 mm (or more) margin is typically
![]()
Figure 5. Average absolute error and standard deviation for four regions of the left and right lungs for (a) Patient 1, (b) Patient 2.
![]()
Table 2. Average absolute error of homogenous and heterogeneous models for landmarks at the bifurcation of airway.
![]()
Figure 6. Comparison of prediction displacement for monitored landmarks located at the (a) top (b) middle and (c) bottom of the left lung over the inhalation phase.
![]()
Figure 7. Comparison of prediction displacement for monitored landmarks located at the (a) top (b) middle and (c) bottom of the right lung over the inhalation phase.
associated with motion uncertainty [31] . However, the observed error for the landmarks near the outer surface and the heart is observed to be relatively large. This discrepancy suggests that contact between the lung and chest wall, as well as impact of heart motion should be major areas for further investigation and model improvement.
The predicted displacement was found to be significantly improved by allowing for the heterogeneity of lung tissue. At the bifurcation of the airway, the predicted average AP, LR and SI errors are reduced by 0.39 mm, 1.2 mm, and 2.17 mm respectively for Patient 1. The corresponding values for Patient 2 are 0.41 mm, 0.6 mm, and 1.02 mm.
The 4DCT registration technique provides a direct means to obtain the displacement field from a set of images, but the physiological and physical properties of the lung are not considered. On the other hand, biomechanical modeling enables consideration of the physiology of the breathing process and the physical properties in a dynamical model through the boundary conditions and material properties. However, the necessary simplifications and approximations associated with modeling could affect the accuracy of the results. Thus the need for model validation is as reported here.
A comparison of the results obtained from these two approaches provides a means of assessing sufficiency versus accuracy in the choice of the technique for estimation of lung deformation. A strict separation of biophysical modeling and image registration approaches might, however, be unnecessarily restrictive. The underlying physiological features of biophysical modeling can often lead to an improved image acquisition guidance. For instance, lung segmentation is commonly used to separate the motion field estimation inside the lungs from that for the background in order to account for the discontinuities in lung and chest wall motion [17] [32] . In contrast, biomechanical modeling approaches could benefit by rendering the models more patient-specific through integration with image information [21] . A recent study by the authors represents such an approach in order to improve model accuracy and estimated motion field [33] [34] . Current biomechanical modeling usually ends with extracting geometrical information from the patient’s image data but several studies have reported that diseases could affect tissue properties and motion patterns [19] [35] . For clinical application, the effect of those factors and their integration with biomechanical modeling would be worthy of consideration using the approach in the present study.
The biomechanical model here extends beyond previous studies by utilizing human patient-specific and spatially distributed material properties. In contrast, most of the previous biomechanical modeling studies on human lung have used uniform material constants obtained from experiments on animal tissue or cadaver, which are inadequate for human radiotherapy. Nevertheless, it is still desirable to improve on some assumptions and simplifications used in this study. In particular, labor sliding and contact mechanics of the lungs are being investigated to further improve model accuracy.
Acknowledgements
The work is funded in part by the National Science Foundation under grants numbers 1200841 and 1200579.
NOTES
![]()
*Corresponding author.