Dynamic Behavior Induced by the Cooperation between Two Different Ionic Conductances in a Mathematical Model of Vibrissa Motoneurons ()
Received 16 April 2016; accepted 12 June 2016; published 15 June 2016

1. Introduction
Neurons are examples of nonlinear dynamical systems, and their dynamics is investigated by various types of mathematical models based on the Hodgkin-Huxley equations [1] . As an example of such mathematical models, a vibrissa motoneuron model (vMN model) has been proposed [2] . This model is described by a system of nonlinear ordinary differential equations (ODEs) and comprises several voltage-dependent ionic conductances: the transient sodium conductance, the persistent sodium conductance, the delayed-rectifier potassium conductance, and three types of slow ionic conductances (the slowly activating potassium afterhyperpolarization (AHP) conductance, the hyperpolarization-activated h conductance, and the potassium M conductance) (see Methods in ref. [2] ). The vMN model shows various types of interesting dynamical behavior, such as repetitive spiking [2] , mixed-mode oscillations [3] , and bistability, between resting and spiking states [3] . It is important to understand the relationship between the ionic conductance and various dynamical behaviors of the vMN model, and several results that reveal such relationships have been reported so far, for examples, the transient sodium conductance (but not the persistent sodium conductance) is essential for generating repetitive spiking [4] ; the frequency of repetitive spiking is modulated by the AHP conductance and the h conductance [2] , the h conductance is involved in mixed-mode oscillations [3] , and the h conductance and the M conductance are involved in bistability between the resting and spiking states [3] .
Investigation of the effect of simultaneous variations in several ionic conductance values on the dynamical behavior of neuron models has been extensively performed not only in the vMN model [4] but also in other neuron models [5] - [9] . For example, the analysis of simultaneous variations in transient and persistent sodium conductances has revealed that in the vMN model, the former conductance plays a more important role in generating repetitive spiking than the latter [4] . However, the analysis of simultaneous variations in sodium and slow ionic conductances has not been performed in detail in the vMN model. Investigation of this issue may contribute to a detailed understanding of the relationship between the ionic conductance and dynamical behavior of the vMN model. Therefore, in the present study, a computer simulation analysis of the vMN model was performed to investigate the effect of variations in the transient sodium and the two types of slow ionic conductance (the AHP conductance and the h conductance) on the dynamical behavior. (In the vMN model, there are two types of sodium conductance. However, since the transient sodium conductance is considered to be more important than the persistent sodium conductance [4] , the present study focuses only on the transient sodium conductance. In addition, to make the vMN model simpler, the present study does not consider the M conductance).
2. Materials and Methods
The present study performed numerical simulation of the vMN model, which is described by a system of nonlinear ODEs. As the detailed explanations of the vMN model have been given previously [2] , we describe the vMN model only briefly here. The equations describing the vMN model are as follows:
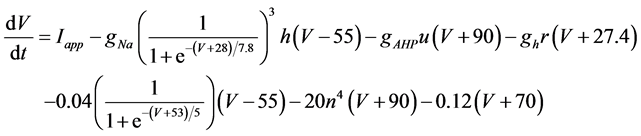 (1)
(1)
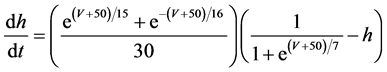 (2)
(2)
 (3)
(3)
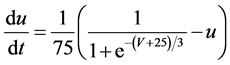 (4)
(4)
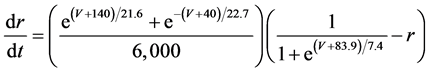 (5)
(5)
where V (mV), h, n, u, and r are state variables (V is the membrane potential of the vMN model, and h, n, u, and r are gating variables of ionic currents), t (ms) is time, Iapp (mA/cm2) is an external stimulation (in the present study, an Iapp of 2.5 mA/cm2 was applied to the vMN model between 1.0 s and 1.5 s, otherwise Iapp was held zero.), gNa, gAHP, and gh are maximal conductances of the transient sodium current, the AHP current, and the h-current, respectively. (Default values are gNa = 100.0 mS/cm2, gAHP = 10.0 mS/cm2, and gh = 0.05 mS/cm2. In the present study, these three conductance values were varied.).
The free and open source software Scilab (http://www.scilab.org/) was used to numerically solve the ODEs (initial conditions: V = -65.84 mV, h = 0.92141213, n = 0.0497938, u = 0.00040176, r = 0.095137881).
3. Results
First, the effect of variations in gNa and gAHP on the response of the vMN model to an external stimulation was examined. Figure 1(a) shows the time course of the membrane potential under conditions in which both gNa and gAHP are at default values. Before stimulation, the membrane potential was in a steady state (we define this state as the “down state”). During stimulation, repetitive spiking appeared. After the stimulation, the membrane potential recovered to the pre-stimulation level. Figure 1(b) shows the time course of the membrane potential under conditions in which gNa is at default value but gAHP is zero. The time course of the membrane potential was similar to that shown in Figure 1(a). A remarkable difference between Figure 1(a) and 1B was that the frequency of repetitive spiking shown in Figure 1(b) was much larger than that shown in Figure 1(a). Figure 1(c) shows the time course of the membrane potential under conditions in which gNa is zero but gAHP is at default value. The state of the membrane potential both before and after the stimulation was similar to those shown in Figure 1(a) and Figure 1(b). In contrast, during the stimulation, although the membrane potential slightly depolarized, repetitive spiking did not occur. Figure 1(d) shows the time course of the membrane potential under conditions wherein both gNa and gAHP are zero. The state of the membrane potential before the stimulation was similar to that shown in Figures 1(a)-(c). The state of the membrane potential during the stimulation was similar to that shown in Figure 1(c). Interestingly, in contrast to Figures 1(a)-(c), after the stimulation, the membrane potential did not return to the pre-stimulation level but instead stabilized at a slightly depolarized steady state
![]()
Figure 1. Time courses of the membrane potential of the vMN model at different values of gNa and gAHP. (a) (gNa, gAHP) = (100.0, 10.0); (b) (gNa, gAHP) = (100.0, 0.0); (c) (gNa, gAHP) = (0.0, 10.0); (d) (gNa, gAHP) = (0.0, 0.0). Through- out (a) to (d), gh was held at 0.05 mS/cm2.
(we define this state as the “up state”) which continued even in the absence of an external stimulation.
Next, the effect of variations in gNa and gh on the response of the vMN model to an external stimulation was examined (Figure 2). Under conditions wherein both gNa and gh were at default values, the time course of the membrane potential was the same as that shown in Figure 1(a) (Figure 2(a)). A tendency similar to that shown in Figure 2(a) was observed under conditions wherein gNa was at default value but gh was zero (Figure 2(b)). Under conditions in which gNa was zero but gh was at default value, the time course of the membrane potential was the same as that shown in Figure 1(c) (Figure 2(c)). When both gNa and gh were zero, a similar pattern as in Figure 2(c) was observed (Figure 2(d)). A remarkable difference between Figure 1 and Figure 2 is that when gNa was zero, the up state appeared under conditions in which gAHP was zero but not under conditions in which gh was zero (compare Figure 1(d) and Figure 2(d)).
Since Figure 1(d) indicates that the elimination of both gNa and gAHP plays an important role in inducing the stimulation-induced transition from the down state to the up state, we performed numerical simulation further focusing on the relationship between the transition and the levels of these two conductances in detail. We systematically varied the values of gNa and gAHP and investigated whether the transition had occurred or not (Figure 3). When gNa was relatively large (e.g., gNa = 5.0 mS/cm2), the transition did not occur irrespective of the gAHP value. Similarly, when gAHP was relatively large (e.g., gAHP = 0.4 or 0.5 mS/cm2), the transition did not occur irrespective of the gNa value. In other words, for the transition to occur, it is necessary (but not sufficient) to satisfy two conditions simultaneously: (1) gNa was 4.0 mS/cm2 or less and (2) gAHP was 0.3 mS/cm2 or less. When gNa was between 2.0 and 4.0 mS/cm2, the gAHP range in which the transition occurred was 0.0 - 0.3 mS/cm2. When gNa was between 0.0 and 1.0 mS/cm2, the gAHP range in which the transition occurred was 0.0 - 0.2 mS/cm2.
4. Discussion
The present study varied the values of gNa, gAHP, and gh of the vMN model to reveal the effect of variations in these values on the response of the vMN model to an external stimulation. In particular, by appropriately modulating the values of gNa and gAHP (e.g., Figure 1(d) and Figure 3), a transiently applied external stimulation can transform the dynamical state of the vMN model from the down state to the up state. This indicates that under certain conditions, the vMN model can show bistability between the up and down states, which has not been re-
![]()
Figure 2. Time courses of the membrane potential of the vMN model at different values of gNa and gh. (a) (gNa, gh) = (100.0, 0.05); (b) (gNa, gh) = (100.0, 0.00); (c) (gNa, gh) = (0.0, 0.05); (d) (gNa, gh) = (0.0, 0.00). Throughout (a) to (d), gAHP was held at 10.0 mS/cm2.
![]()
Figure 3. The dependence of the stimulation-triggered transition from a down state to an up state on gNa and gAHP. ○: the transition did not occur, ●: the transition occurred. gh was held at 0.05 mS/cm2.
ported in previous studies of the vMN model. Although previous studies have indicated that the vMN model shows bistability under certain conditions, it is different from the bistability described in the present study as it is the bistability between the resting and spiking states [3] .
Previous studies of various types of mathematical neuron models have shown various types of bistability. Several examples have been reported: (1) bistability between periodic spiking and bursting states [10] - [12] ; (2) bistability between period-2 spiking and bursting states [13] ; (3) bistability between period-4 spiking and bursting states [13] ; (4) bistability between chaotic spiking and bursting states [14] [15] ; (5) bistability between two period-1 spiking states [16] ; (6) bistability between period-1 spiking and period-2 spiking states [16] ; (7) bistability between period-1 spiking and period-4 spiking states [16] ; (8) bistability between period-1 spiking and chaotic spiking states [16] ; (9) bistability between resting and spiking states [3] [7] [12] ; and (10) bistability between resting and bursting states [12] [17] . Here, we consider a simple classification of bistability into three types: (a) bistability between oscillatory and steady states; (b) bistability between two oscillatory states; and (c) bistability between two steady states. Based on this classification scheme, the bistabilities from (1) to (8) correspond to type (b) and those from (9) and (10) correspond to the type (a); however, we cannot find type (c) within the bistabilities (1) to (10). The bistability revealed in the present study, which is bistability between the up and down states, is classified as type (c).
The present study indicates that simultaneous variations in ionic conductance values are useful for understanding the relationship between ionic conductances and the dynamical behavior of neuron models. The transition from the down state to the up state, which is described in the present study (Figure 1 and Figure 3), was observed by simultaneously modulating both gNa and gAHP, while the modulation of neither gNa alone nor gAHP alone can induce the transition. In other words, the present results reveal that a simultaneous decrease in gNa and gAHP plays an important role in inducing a transition from the down state to the up state. The effect of the cooperation between different ionic conductances on the dynamical behavior of neuron models has also been described in a previous report: under certain conditions, neither a decrease in gNa alone nor a decrease in gCa alone cannot stop pacemaking in a dopaminergic neuron model, but a simultaneous decrease in both gNa and gCa can [5] . However, the combination of ionic conductances involved in the cooperative effect is different between the present (Figure 1 and Figure 3) and the previous studies [5] .
5. Conclusion
The following are the important findings of the present study: (1) under certain conditions, the vMN model can change the dynamical state from the down state to the up state in response to a transient external perturbation, which is a novel type of bistability that was not described in previous studies of the vMN model and (2) the change from the down state to the up state is induced by a simultaneous decrease in gNa and in gAHP. The present study contributes to an in-depth understanding of the relationship between ionic conductances and the dynamical behavior of the vMN model.
Acknowledgements
The author would like to thank Enago (www.enago.jp) for their review of the English language.