Received 3 May 2016; accepted 11 June 2016; published 14 June 2016

1. Introduction
By a natural extension of the fractions
 (1)
(1)
for any complex numbers a and b, we found the simple and beautiful result, for any complex number b
 (2)
(2)
incidentally in [1] by the Tikhonov regularization for the Hadamard product inversions for matrices and we discussed their properties and gave several physical interpretations on the general fractions in [2] for the case of real numbers. The result is a very special case for general fractional functions in [3] .
The division by zero has a long and mysterious story over the world (see, for example, Google site with the division by zero) with its physical viewpoints since the document of zero in India on AD 628; however, Sin-Ei Takahasi ( [2] ) established a simple and decisive interpretation (2) by analyzing the extensions of fractions and by showing the complete characterization for the property (2):
Proposition 1. Let F be a function from  to
to  satisfying
satisfying

for all

and
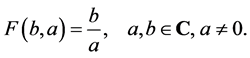
Then, we obtain, for any 

Note that the complete proof of Proposition 1 is simply done with 2 or 3 lines.
We thus should consider, for any complex number b, as (2); that is, for the mapping
 (3)
(3)
the image of  is
is  (should be defined). This fact seems to be a curious one in connection with our well-established popular image for the point at infinity on the Riemann sphere ( [4] ). Therefore, the division by zero will give great impacts to complex analysis and to our ideas for the space and universe.
(should be defined). This fact seems to be a curious one in connection with our well-established popular image for the point at infinity on the Riemann sphere ( [4] ). Therefore, the division by zero will give great impacts to complex analysis and to our ideas for the space and universe.
However, the division by zero (2) is now clear; indeed, for the introduction of (2), we have several independent approaches as in:
1) by the generalization of the fractions by the Tikhonov regularization or by the Moore-Penrose generalized inverse,
2) by the intuitive meaning of the fractions (division) by H. Michiwaki,
3) by the unique extension of the fractions by S. Takahasi, as in the above,
4) by the extension of the fundamental function  from
from  into
into  such that
such that ![]() is a one to one and onto mapping from
is a one to one and onto mapping from ![]() onto
onto ![]() and the division by zero
and the division by zero ![]() is a one to one and onto mapping extension of the function
is a one to one and onto mapping extension of the function ![]() from
from ![]() onto
onto![]() , and
, and
5) by considering the values of functions with the mean values of functions.
Furthermore, in ( [5] ) we gave the results in order to show the reality of the division by zero in our world:
A) a field structure containing the division by zero―the Yamada field![]() ,
,
B) by the gradient of the y axis on the ![]() plane―
plane―![]() ,
,
C) by the reflection ![]() of
of ![]() with respect to the unit circle with center at the origin on the complex z plane―the reflection point of zero is zero, and
with respect to the unit circle with center at the origin on the complex z plane―the reflection point of zero is zero, and
D) by considering rotation of a right circular cone having some very interesting phenomenon from some practical and physical problem.
Meanwhile, J. P. Barukcic and I. Barukcic ( [7] ) discussed recently the relation between the division 0/0 and special relative theory of Einstein.
Furthermore, T. S. Reis and J.A.D.W. Anderson ( [8] [9] ) extend the system of the real numbers containing division by zero.
Meanwhile, we should refer to up-to-date information:
Riemann Hypothesis Addendum―Breakthrough
Kurt Arbenz: https://www.researchgate.net/publication/272022137 Riemann Hypothesis Addendum―Break- through.
Here, we recall Albert Einstein’s words on mathematics: Blackholes are where God divided by zero. I don’t believe in mathematics. George Gamow (1904-1968) Russian-born American nuclear physicist and cosmologist remarked that “it is well known to students of high school algebra” that division by zero is not valid; and Einstein admitted it as the biggest blunder of his life (Gamow, G., My World Line (Viking, New York). p 44, 1970).
For the definitions ![]() and (2), we should note that they are not the usual fractions defined by
and (2), we should note that they are not the usual fractions defined by ![]() and
and ![]() as the inverses of products that mean contradictions, immediately. They are just given as definitions for the pairs
as the inverses of products that mean contradictions, immediately. They are just given as definitions for the pairs ![]() and
and![]() , respectively. This precise meaning is given by Proposition 1. Note that for the introduction of the Y-field ( [5] ) containing the division by zero, the meaning is the same. For calculations containing the division by zero, we can apply the Y-field laws. In particular, note that the general product property
, respectively. This precise meaning is given by Proposition 1. Note that for the introduction of the Y-field ( [5] ) containing the division by zero, the meaning is the same. For calculations containing the division by zero, we can apply the Y-field laws. In particular, note that the general product property
![]() (4)
(4)
and
![]() (5)
(5)
are valid and the sum is given by
![]()
However, the sum law
![]() (6)
(6)
is, in general, not valid, however, if ![]() or
or![]() , then the sum law is valid, and further properties for the general fractions, see ( [10] ).
, then the sum law is valid, and further properties for the general fractions, see ( [10] ).
In this paper, we will discuss the division by zero in matrices and we will be able to see that the division by zero is our elementary and fundamental mathematics. We will introduce a new space for the Euclidean plane. Indeed, for the point at infinity on the Riemann sphere, we will introduce a new idea and fact.
2. Division by Zero in Cramer’s Law
We will recall the elementary Cramer’s law. We write lines by
![]() (7)
(7)
The common point ![]() is given by, if
is given by, if![]() ; that is, the lines are not parallel, by the Cramer’s law
; that is, the lines are not parallel, by the Cramer’s law
![]() (8)
(8)
By the division by zero, we can understand that if![]() , then the common point is always given by
, then the common point is always given by
![]() (9)
(9)
even when the two lines are the same.
The division by zero, in particular, means, surprisingly, that the point at infinity is represented by zero, that is, the coincidence of the point at infinity and the origin. Precisely, the point at infinity (topological point) is represented by ![]() with the number. The point at infinity is a point of one-point compactification of Aleksandrov and is not represented by the number of the infinity as in the common sense. We can see that the whole line on the plane passes the point at infinity, by the stereographic projection into the Riemann sphere. The point at infinity is represented by the zero
with the number. The point at infinity is a point of one-point compactification of Aleksandrov and is not represented by the number of the infinity as in the common sense. We can see that the whole line on the plane passes the point at infinity, by the stereographic projection into the Riemann sphere. The point at infinity is represented by the zero ![]() and so, every line on the plane passes the origin in this sense.
and so, every line on the plane passes the origin in this sense.
This fact may be understood that the point at infinity is reflected to the origin. In this sense, the origin will have double natures of the native origin and reflection of the point at infinity. The latter has a strong discontinuity.
3. The Point at Infinity
We will be able to see the whole Euclidean plane by the stereographic projection into the Riemann sphere―We think that in the Euclidean plane, there does not exist the point at infinity.
However, we can consider it as a limit like ¥. Recall the definition of ![]() by e-d logic; that is,
by e-d logic; that is, ![]() if and only if for any large
if and only if for any large![]() , there exists a number
, there exists a number ![]() such that for any z satisfying
such that for any z satisfying![]() ,
,![]() . In this definition, the infinity ¥ does not appear. The infinity is not a number, but it is an ideal space point―one-point compactification of Aleksandrov.
. In this definition, the infinity ¥ does not appear. The infinity is not a number, but it is an ideal space point―one-point compactification of Aleksandrov.
The behavior of the space around the point at infinity may be considered by that around the origin by the linear transform ![]() ( [4] ). We thus see that
( [4] ). We thus see that
![]() (10)
(10)
however,
![]() (11)
(11)
by the division by zero. Here, ![]() denotes the value of the function
denotes the value of the function ![]() at the topological point at the infinity in one point compactification by Aleksandrov. The difference of (10) and (11) is very important as we see clearly by the function
at the topological point at the infinity in one point compactification by Aleksandrov. The difference of (10) and (11) is very important as we see clearly by the function ![]() and the behavior at the origin. The limiting value to the origin and the value at the origin are different. For surprising results, we will state the property in the real space as follows:
and the behavior at the origin. The limiting value to the origin and the value at the origin are different. For surprising results, we will state the property in the real space as follows:
![]() (12)
(12)
however,
![]() (13)
(13)
Of course, two points ![]() and
and ![]() are the same point as the point at infinity. However, ± will be convenient in order to show the approach directions.
are the same point as the point at infinity. However, ± will be convenient in order to show the approach directions.
4. Interpretation by Area
In order to see some realization of the properties of (12) and (13), we will consider the triangle with the basic edge (side) a and high h. Then, the area S of the triangle is given by
![]() (14)
(14)
By fixing the high h and the line containing the side a, we will consider the limiting![]() . Then, of course,
. Then, of course,
![]() (15)
(15)
However, we will see that
![]() (16)
(16)
just like the division by zero, because, when![]() , the triangle is broken, we cannot consider the area of the triangle. Here, the notation
, the triangle is broken, we cannot consider the area of the triangle. Here, the notation ![]() is not good, however, its meaning is clear; it will mean the case of parallel lines of the line containing the side a and the line through the fixed vertex of the triangles when we consider a tending to
is not good, however, its meaning is clear; it will mean the case of parallel lines of the line containing the side a and the line through the fixed vertex of the triangles when we consider a tending to![]() .
.
The strong discontinuity of the division by zero is appeared as the broken of the triangles. These phenomena may be looked in many situations as the universe one. We can consider similar problems for many types volumes. However, the simplest cases are disc and sphere (ball) with radius 1/R. When![]() , the areas and volumes tend to
, the areas and volumes tend to![]() , however, when
, however, when![]() , they are zero, because they become the half-plane and half-space, respectively.
, they are zero, because they become the half-plane and half-space, respectively.
5. Interpretation by Analytic Geometry
The results in Section 4 may be interpreted beautifully by analytic geometry and matrix theory.
We write lines by
![]() (17)
(17)
The area S of the triangle surrounded by these lines is given by
![]() (18)
(18)
where ![]() is
is
![]()
and ![]() is the co-factor of
is the co-factor of ![]() with respect to
with respect to![]() .
. ![]() if and only if the corresponding lines are parallel.
if and only if the corresponding lines are parallel. ![]() if and only if the three lines are parallel or they have a common point. We can see that the degeneracy (broken) of the triangle may be interpreted by
if and only if the three lines are parallel or they have a common point. We can see that the degeneracy (broken) of the triangle may be interpreted by ![]() beautifully, by the division by zero.
beautifully, by the division by zero.
For a function
![]() (19)
(19)
the radius R of the circle ![]() is given by
is given by
![]() (20)
(20)
If![]() , then the area
, then the area ![]() of the disc is zero, by the division by zero; that is, the circle is a line (degenerate).
of the disc is zero, by the division by zero; that is, the circle is a line (degenerate).
When we apply the division by zero to functions, we can consider, in general, many ways.
For example, for the function![]() , when we insert
, when we insert ![]() in numerator and denominator, we have
in numerator and denominator, we have
![]() (21)
(21)
However, from the identity―the Laurent expansion around![]() ,
,
![]() (22)
(22)
we have
![]() (23)
(23)
For analytic functions we can give uniquely determined values at isolated singular points by the values by means of the Laurent expansions as in (22), however, the values by means of the Laurent expansions are not always reasonable. We will need to consider many interpretations for reasonable values. In many formulas in mathematics and physics, we can see that the division by zero is valid. See [2] [5] . In connection with lines, we will state examples.
The center of the circle (19) is given by
![]() (24)
(24)
Therefore, the center of a general line
![]() (25)
(25)
may be considered as the origin![]() , by the division by zero.
, by the division by zero.
We consider the functions
![]() (26)
(26)
The distance d of the centers of the circles ![]() and
and ![]() is given by
is given by
![]() (27)
(27)
If![]() , then by the division by zero
, then by the division by zero
![]() (28)
(28)
Then, ![]() is a line and its center is the origin
is a line and its center is the origin![]() . Therefore, the result is very reasonable.
. Therefore, the result is very reasonable.
Meanwhile, the identity ![]() is valid always, however
is valid always, however ![]() is not valid for
is not valid for![]() , in the sense of the division by zero, because we consider the formula at
, in the sense of the division by zero, because we consider the formula at![]() , with not the limiting values.
, with not the limiting values.
6. Interpretation with Volumes
We write four planes by
![]() (29)
(29)
The volume V of the tetrahedron surrounded by these planes is given by
![]() (30)
(30)
where ![]() is
is
![]()
and ![]() is the co-factor of
is the co-factor of ![]() with respect to
with respect to![]() .
. ![]() if and only if two planes of the corresponding three planes are parallel.
if and only if two planes of the corresponding three planes are parallel. ![]() if and only if the four planes
if and only if the four planes ![]() contain four lines
contain four lines ![]() (for each k, respectively) that are parallel or have a common line. We can see that the degeneracy of the tetrahedron may be interpreted by
(for each k, respectively) that are parallel or have a common line. We can see that the degeneracy of the tetrahedron may be interpreted by ![]() beautifully, by the division by zero.
beautifully, by the division by zero.
7. In the Torsion Formula
For the torsion formula
![]() (31)
(31)
if![]() , then
, then![]() , by the division by zero. This result will be natural than infinity, in the common sense.
, by the division by zero. This result will be natural than infinity, in the common sense.
8. In Spring or Circut
We will give a typical physical example of the division by zero.
We will consider a spring with two spring constants ![]() in a line. Then, the spring constant k of the spring is given by the formula
in a line. Then, the spring constant k of the spring is given by the formula
![]() (32)
(32)
by Hooke’s law. We know, in particular, if![]() , then
, then
![]() (33)
(33)
and by the division by zero,
![]() (34)
(34)
that is very reasonable. In particular, by Hooke’s law, we see that
![]() (35)
(35)
The corresponding result for the case of Ohmu’s law is similar and valid.
9. In Differential Equations
We will consider the fundamental ordinary differential equation
![]() (36)
(36)
satisfying the initial conditions
![]() (37)
(37)
Then we have the solution
![]() (38)
(38)
with
![]()
Then, for![]() , we obtain, immediately, by the division by zero, since
, we obtain, immediately, by the division by zero, since![]() ,
,
![]() (39)
(39)
In this case, by continuity we can obtain the same result:
![]()
However, in the next example, we will need essentially the concept of the division by zero.
We will consider the typical ordinary differential equation
![]() (40)
(40)
satisfying the initial conditions
![]() (41)
(41)
Then we have the solution
![]() (42)
(42)
Then, if![]() , we obtain, immediately, by the division by zero
, we obtain, immediately, by the division by zero
![]() (43)
(43)
Furthermore, if![]() , then have
, then have
![]() (44)
(44)
We can find many and many such examples.
10. Conclusions
By the division by zero![]() , we can give new and practical meanings for many mathematical and physical formulas for the denominator zero cases. We introduced the new space idea for the point at infinity for the Eucleadian plane. This new idea will give great impacts on our general ideas on the universe over mathematics.
, we can give new and practical meanings for many mathematical and physical formulas for the denominator zero cases. We introduced the new space idea for the point at infinity for the Eucleadian plane. This new idea will give great impacts on our general ideas on the universe over mathematics.
In the sense of the division by zero, the number of infinity should be excluded; however, in limits we can consider the infinity in the common sense. We should distinguish the infinity in the senses of a point at infinity in one point compactification and of the infinity in some limit. The point at infinity in one point compactification is represented by the number![]() .
.
Acknowledgements
The first author is supported in part by the Grant-in-Aid for the Scientific Research (C) (2) (No. 26400192). Saitoh wishes to express his deep thanks Professor Haydar Akca for his kind invitation of the paper ( [5] ) based on recent results for the division by zero and Professor Jan Bergstra for his kind suggestions on this paper. The authors wish to express their sincere thanks to Dr. Masako Takagi for her kind suggestions for the manuscript.