Equivalence of Uniqueness in Law and Joint Uniqueness in Law for SDEs Driven by Poisson Processes ()
Received 23 November 2015; accepted 17 May 2016; published 20 May 2016

1. Introduction
There are several types of solutions and uniqueness for stochastic differential equations, such as strong solution, weak solution, pathwise uniqueness, uniqueness in law and joint uniqueness in law, which will be introduced in Section 2. The relationship between them was firstly studied by Yamada and Watanabe [1] . They got

and

which is the famous Yamada-Watanabe theorem. It’s an important method to prove the existence of strong solution for SDEs Nowadays. The study on this topic is still alive today and new papers are published, see [2] - [10] . On the other hand, Jacod [11] and Engelbert [12] extended the Yamada-Watanabe theorem to the stochastic differential equation driven by semi-martingales. Especially, Engelbert got an inverse result, that is


where ,
,  and
and 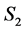 are Polish spaces. They obtained an unified result ( [7] Theorem 1.5):
are Polish spaces. They obtained an unified result ( [7] Theorem 1.5):

which was called the Yamada-Watanabe-Engelbert thereom. This result can cover most results mentioned above. However, joint uniqueness in law is harder to check than uniqueness in law in view of application. The natural question that arises now is: under what conditions, joint uniqueness can be equivalent to uniqueness in law? Kurtz ( [5] [7] ) gave a positive answer for the stochastic equations of the form

when the constrains are simple (linear) equations. It’s sad that the stochastic differential equations are not of the form above, therefore the equivalence does not follow from this result.
There exist few results for this question. As far as we know, Cherny [14] and Brossard [13] proved the equivalence of uniqueness in law and joint uniqueness in law for Itô equations of the following type

driven by Brownian motion with the coefficients which only need to be measurable. Later, Qiao [15] extended the result of [14] to a type of infinite dimensional stochastic differential equaion. For stochastic differential equations with jumps, there is still no such result. So, in this paper, we are concerned with the following one- dimensional stochastic differential equation driven by Poisson process
 (1.1)
(1.1)
We will give an extension form of Watanabe’s characterization for 2-dimensional Poisson process, then by applying Cherny’s approach, we prove the equivalence of the uniqueness in law and joint uniqueness in law for Equation (1).
This paper is organized as follows. In Section 2, we prepapre some notations and some definitions. After that, the main results are given and proved in Section 3.
2. Notations and Definitions
Let  be the space of all càdlàg functions:
be the space of all càdlàg functions:  and let
and let  denote the s-algebra generated by all the maps
denote the s-algebra generated by all the maps ,
, ![]() , where
, where![]() ,
,![]() . Let
. Let![]() .
.
Definition 2.1. Let ![]() be a probability space with a given filtration
be a probability space with a given filtration![]() , and let
, and let ![]() be a deterministic function of time. A counting process N is a Poisson process with intensity function
be a deterministic function of time. A counting process N is a Poisson process with intensity function ![]() with respect to the filtration
with respect to the filtration ![]() if it satisfies the following conditions.
if it satisfies the following conditions.
1) N is adapted to![]() ;
;
2) For all ![]() the random variable
the random variable ![]() is independent of
is independent of![]() ;
;
3) For all![]() , the conditional distribution of the increment
, the conditional distribution of the increment ![]() is given by
is given by
![]()
where
![]()
Definition 2.2. Let ![]() be a probability space with a given filtration
be a probability space with a given filtration![]() , and let
, and let![]() ,
, ![]() be two deterministic function of time.
be two deterministic function of time. ![]() and
and ![]() are two F-Poisson processes with intensity function
are two F-Poisson processes with intensity function ![]() and
and ![]() respectively. Process
respectively. Process ![]() is called a 2-dimensional F-Poisson process with intensity function
is called a 2-dimensional F-Poisson process with intensity function ![]() if
if ![]() and
and ![]() are independent.
are independent.
We have the following Watanabe characterization for one dimensional Poisson process (see [16] ).
Lemma 2.3. Let ![]() be a probability space with a given filtration
be a probability space with a given filtration![]() . Assume that N is a counting process and that
. Assume that N is a counting process and that ![]() is a deterministic function. Assume furthermore that the process M, defined by
is a deterministic function. Assume furthermore that the process M, defined by
![]()
is an F-martingale. Then N is a F-Poisson process with intensity function![]() .
.
In this paper, we consider the following stochastic differential equation driven by the Poisson process
![]() (2.1)
(2.1)
where ![]() and
and ![]() are
are![]() ―measurable and for each
―measurable and for each![]()
![]() ,
, ![]() and
and ![]() are predictable.
are predictable.
Definition 2.4. A pair![]() , where
, where ![]() is a càdlàg
is a càdlàg ![]() -adapted process with paths in
-adapted process with paths in ![]() and N is a Poisson process with intensity function
and N is a Poisson process with intensity function ![]() on a stochastic basis
on a stochastic basis![]() , is called a weak solution of (2.1) if
, is called a weak solution of (2.1) if
1) For all![]() ,
,
![]()
2) For all![]() ,
,
![]()
Definition 2.5. We say that uniqueness in law holds for (2.1) if whenever ![]() and
and ![]() are two weak solutions with stochatic bases
are two weak solutions with stochatic bases ![]() and
and ![]() such that
such that
![]()
then
![]()
Definition 2.6. We say that joint uniqueness in law holds for (2.1) if whenever ![]() and
and ![]() are two weak solutions with stochatic bases
are two weak solutions with stochatic bases ![]() and
and ![]() such that
such that
![]()
then
![]()
Definition 2.7. We say that pathwise uniqueness holds for (1.1) if whenever ![]() and
and ![]() are two weak solutions on the same stochatic bases
are two weak solutions on the same stochatic bases ![]() such that
such that ![]() P-a.s., then P-a.s.
P-a.s., then P-a.s.
![]()
3. Main Results
Theorem 3.1. Suppose that the uniqueness in law holds for (2.1). Then, for any solutions ![]() and
and![]() , the law of
, the law of ![]() and the law of
and the law of ![]() are equal on
are equal on![]() , that is
, that is
![]()
According to Theorem 1.5 of Kurtz [7] , we have the following simplified Yamada-Watanabe-Engelbert theorem (see aslo [12] Theorem 3, [14] Theorem 3.2) immediately.
Corollary 3.2. The following are equivalent:
1) Equation (2.1) has a strong solution and uniqueness in law holds;
2) Equation (2.1) has a weak solution and pathwise uniqueness holds.
![]()
We have the following generalised martingale characterization for 2-dimensional Poisson processes, which may have its own interest.
Lemma 3.3. Let ![]() be a probability space with a given filtration
be a probability space with a given filtration![]() . Assume that
. Assume that ![]() is a 2-dimensional counting process and that
is a 2-dimensional counting process and that ![]() are two deterministic function. Then, N is a 2-dimensional F-Poisson process with intensity function
are two deterministic function. Then, N is a 2-dimensional F-Poisson process with intensity function ![]() is equivalent to the following two conditions.
is equivalent to the following two conditions.
1) Processes ![]() and
and ![]() defined by
defined by
![]()
are F-martingales.
2) Process N defined by
![]()
is a F―Poisson process with intensity function![]() .
.
Proof. By Lemma 2.3, we only need to prove that two Poisson processes are independent if and only if their sum is also a Poisson process.
Suppose that ![]() and
and ![]() are two independent Poisson processes. For
are two independent Poisson processes. For![]() , we have,
, we have,
![]()
By the independence of ![]() and
and![]() , for each
, for each![]() , we obtain
, we obtain
![]()
We conclude that![]() , which tell us that N is a counting process. Furthermore, we have process defined by
, which tell us that N is a counting process. Furthermore, we have process defined by
![]()
is a martingale. By the Watanabe’s result, we have that N is a Poisson process with intensity function![]() .
.
On the other hand, suppose that ![]() be a Poisson process, we aim to prove that
be a Poisson process, we aim to prove that ![]() and
and ![]() are independent. In fact, let
are independent. In fact, let ![]() and
and![]() ,
, ![]() , we have
, we have
![]()
which completes the proof.
We will recall the concept of conditional distribution from the measure theory. Let ![]() be a random element on
be a random element on ![]() taking value in a Polish space
taking value in a Polish space![]() . Let
. Let![]() , then there exists a conditional distribution of
, then there exists a conditional distribution of ![]() with respect to
with respect to![]() , that is, a family
, that is, a family ![]() of probability measures on
of probability measures on ![]() such that
such that
1) For any![]() , the map
, the map ![]() is
is ![]() -measurable;
-measurable;
2) For any![]() ,
, ![]() ,
,
![]()
Remark 3.4. 1) The conditional distribution defined above is unique in the sense: if ![]() is another family probability measures with the same properties, then
is another family probability measures with the same properties, then ![]() for P-a.e.
for P-a.e.![]() .
.
2) If ![]() is such that
is such that![]() , then
, then ![]() for P-a.e.
for P-a.e.![]() .
.
Lemma 3.5. Let ![]() be a weak solution of (2.1) on a filtered probability space
be a weak solution of (2.1) on a filtered probability space![]() . Let
. Let ![]() be a conditional distribution of
be a conditional distribution of ![]() with respect to
with respect to ![]() (here we consider
(here we consider ![]() as a
as a ![]() -valued random variable). We denote by Y, M the canonical maps from
-valued random variable). We denote by Y, M the canonical maps from ![]() onto
onto ![]() respectively, that is
respectively, that is
![]()
and
![]()
Let
![]()
![]()
Then, for P-a.e.![]() , the pair
, the pair ![]() is a weak solution of (2.1) on
is a weak solution of (2.1) on![]() .
.
Proof. Let us check the conditions of Definition 2.4.
1) Firstly, we will check that M is an ![]() -Poisson process. For any
-Poisson process. For any![]() ,
, ![]() ,
, ![]() , we have
, we have
![]()
where ![]() is defined as in Definition 2.1. Hence, we have
is defined as in Definition 2.1. Hence, we have
![]()
It follows that
![]()
Therefore, for P-a.e.![]() ,
,
![]()
We deduce that, for P-a.e![]() , M is an
, M is an ![]() -Poisson process with intensity function
-Poisson process with intensity function![]() .
.
2) For any![]() ,
,
![]()
By Remark 3.4, we have
![]()
for P-a.e.![]() .
.
3) We have
![]()
Hence,
![]()
for P-a.e.![]() .
.
Proof of Theorem 3.1. Let ![]() be a weak solution of (2.1) on a filtered space
be a weak solution of (2.1) on a filtered space![]() . Let
. Let ![]() and
and ![]() be two independent
be two independent ![]() -Poisson processes with the same intensity function
-Poisson processes with the same intensity function![]() . Set
. Set
![]()
Then X, N, ![]() and
and ![]() can be defined on
can be defined on ![]() in an obvious way. The pair
in an obvious way. The pair ![]() is a solution of (2.1) on
is a solution of (2.1) on ![]() and
and![]() ,
, ![]() are independent
are independent ![]() -Poisson processes. For any
-Poisson processes. For any![]() , and
, and![]() ,
, ![]() is a linear operator from
is a linear operator from![]() . Let
. Let ![]() denote the orthogonal projection from
denote the orthogonal projection from![]() ; let
; let ![]() denote the orthogonal projection from
denote the orthogonal projection from![]() .
.
For any![]() , set
, set
![]()
![]() (3.1)
(3.1)
We claim that ![]() and
and ![]() are two independent
are two independent ![]() -Poisson processes with the intensity function
-Poisson processes with the intensity function![]() . In fact, it’s easy to see that
. In fact, it’s easy to see that![]() ,
, ![]() and
and ![]() are counting processes. Moreover, Let
are counting processes. Moreover, Let
![]()
![]()
![]()
We have
![]()
![]()
Note that processes ![]() and
and ![]() are predictable precesses and the integrators in the above equations are martingales. We conclude that
are predictable precesses and the integrators in the above equations are martingales. We conclude that ![]() and
and ![]() are martingale, theorefore
are martingale, theorefore ![]() is also a martingale. By Lemma 2.3, we get that
is also a martingale. By Lemma 2.3, we get that ![]() and
and ![]() are two
are two![]() ―Poisson processes with the intensity function
―Poisson processes with the intensity function ![]() and
and ![]() is a
is a![]() ―Poisson processes with the intensity function
―Poisson processes with the intensity function![]() . By Lemma 3.3, we deduce that
. By Lemma 3.3, we deduce that ![]() and
and ![]() are two independent
are two independent ![]() -Poisson processes.
-Poisson processes.
For any![]() , we have
, we have
![]()
Consequently, ![]() is also a solution of (2.1) on
is also a solution of (2.1) on![]() .
.
Let us now consider the filtration
![]()
![]() . Note that, for any
. Note that, for any![]() , the s-fields
, the s-fields ![]() and
and ![]() are indepen- dent. Thus,
are indepen- dent. Thus, ![]() is a
is a ![]() -Poisson process. So, the pair
-Poisson process. So, the pair ![]() is also a solution of (2.1) on
is also a solution of (2.1) on![]() .
.
Let ![]() be a conditional distribution of
be a conditional distribution of ![]() with respect to
with respect to![]() . By Lemma 3.5,
. By Lemma 3.5, ![]() is a solution of (2.1) on
is a solution of (2.1) on ![]() for
for ![]() -a.e.
-a.e.![]() . As the uniqueness in law holds for (2.1), the distribution
. As the uniqueness in law holds for (2.1), the distribution ![]() (which is the conditional distribution of X with respect to
(which is the conditional distribution of X with respect to![]() ) is the same for
) is the same for ![]() -a.e.
-a.e.![]() . This means that the process X is independent of
. This means that the process X is independent of![]() . In particular, X and
. In particular, X and ![]() are independent.
are independent.
For any ![]() and
and![]() , let
, let ![]() be the pseudo inverse of
be the pseudo inverse of![]() . It is easy to check that
. It is easy to check that ![]() is predictable and we have
is predictable and we have![]() . It follows that
. It follows that
![]()
where
![]()
By (3.1), we get
![]()
The process ![]() is a measurable functional of X, while
is a measurable functional of X, while ![]() is independent of X. Thus, the last equation shows that the distribution
is independent of X. Thus, the last equation shows that the distribution ![]() is unique. ,
is unique. ,
Remark 3.6. In this paper, the equivalence of the uniqueness in law and joint uniqueness in law holds when diffusion coefficient may be degenerate. We note that, for the general multidimensional stochastic differential equations with jumps, the equivalence does not hold when the diffusion coefficients are allowed to be degenerate. We will consider in the future study.
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China(Grant No.11401029) and Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ13A010020).