Weibull Statistics Strength Investigation of Synthetic Link Chains Made from Ultra-Strong Polyethylene Fibers ()
Received 30 March 2016; accepted 17 May 2016; published 20 May 2016

1. Introduction
Carrying tension load is typically achieved with cables or chains. Cables offer the best strength to weight ratio, whereas chains offer the possibility to attach hooks in various chain links and thus adjust the working length quickly. Moreover, chains are highly flexible and thus easy to handle and store and they coil easy. This is especially relevant in heavy haulage by load securing of irregular shaped freight on ship decks, train wagons or road trailers. Steel is the traditional material for chains. Steel link chains are very heavy. Synthetic link chains made from ultra-high strength gel-spun polyethylene fibers are recently commercially available. The fibers used for the manufacturing of those chains are Dyneema® fibers. An introduction to these fibers is presented earlier [1] [2] . The present chains, recently introduced [3] - [7] , are made by weaving narrow fabrics from UHMWPE Dyneema® fibers, stacking the obtained fabrics into wound chain links and stitching the end connections with a stitching yarn that is also made from Dyneema® fibers. The resulting synthetic link chains have a design Minimum Breaking Load MBL = 200 kN (~20 metric tons) and a Working Load Limit WLL = 100 kN (~10 metric tons). Since the chain is a recent product, launched to global load securing market just in May 2015, there is a motif to quantify variation in break load for quality control. Therefore, strength scatter has been investigated and reported in the present paper. Figure 1 shows such a synthetic chain being tensioned for lashing a yacht on a ship deck. More details on the chains follow in Chapter 2. The tensile tests and results are presented in Chapter 3. The Weibull data processing is discussed in Chapter 4. Some final discussions and conclusions are presented in Chapter 5.
2. Description of Synthetic Link Chains
Figure 2 visualizes a synthetic link chain as it was tested. The blueish label on the link shows the legally required product information. The eight layer stacked structure of each link provides a “capstan effect”, the friction under load causes load transfer between the layers. The right-hand side of Figure 3 shows the stacked fabric windings of a link, the mentioned capstan effect occurs mainly at the link-link interfaces. Thus the residual load on the stitched end termination is reduced down to less than 1% MBL, being much lower than the strength of the stitched connection. This makes each link highly reliable and intrinsically safe against unravelling. Figure 2 also shows that each link additionally contains a half twist. In fact each link is a Möbius ring (referring to a former 19th century mathematician). The reason for this construction [6] is that for an untwisted link, the contour length along the inside is smaller than along the outside. The displacements upon loading are similar, thus the strain at the inside would be larger, so would be the stress, and fracture would occur at a rather early stage at the inside. In contrast, the Möbius ring is a structure where the inside plane and outside plane are in the same. Consequently, the stress concentration is reduced and a stronger chain is the result. The visualized and tested commercially available chain example, branded as TYCAN®, is certified by DNV-GL for heavy load securing, for tie down,
![]()
Figure 1. Synthetic link chain in use on a ship deck.
![]()
![]()
Figure 3. Connection system of the testing machine to the first chain link with oval shaped red pin.
as well for direct lashing. Some more details can be found on the TYCAN® website [7] . Synthetic link chains are attractive in use; the up to eight times lower weight as compared to steel chains, allows faster and safer handling. Chains are often dropped during handling. Synthetic chains are considerably less noisy when falling than steel chains. They are also softer, so do not abrade or scratch cargo and they protect personnel and equipment against injuries and damages. The chains tested consisted of six links. The nominal length of the chains (pin to pin) was 0.6 meter. All chains were preloaded by the manufacturer to the WLL = 100 kN. The link dimension is 100 mm × 25 mm × 12 mm. The used UHMWPE fibers in warp direction are Dyneema® DM20 dtex1760 and in weft direction Dyneema® SK62 dtex880. The sewing thread is GetaStrong® with Dyneema® from Gruschwitz Fibers GmbH (D). For high reproducibility and reliability, the synthetic link chains are made in an automated way through a streamlined standardized DNV-GL assessed manufacturing process.
3. Tensile Tests on Chains
3.1. Description of the Tests
A number of 50 TYCAN® chains was ordered from the manufacturer and tested as received. A tensile test bench with 900 kN load capacity at an independent external test house was used (Hijs Service Astea B.V., Geleen, The Netherlands). The connection to the loading device was provided by an oval steel pin with a long axis of 60 mm and a short axis of 30 mm. Figure 3 presents an impression of the connection system. The choice for the oval shape was made for providing a large cross section area of the pin without applying a width that opens the link rings too much. Considering the final results it may be concluded in retrospect that still some more opening than desired was apparent. This will be discussed in more detail, later in Chapter 4. The loading rate was 50 mm/minute. This caused a time to fracture of about 50 seconds. The tests were performed at ambient temperature of 17˚C. All load displacement diagrams were recorded up to break. All failures occurred at a link-link interface, sometimes a few fabric layers remained intact after first fracture. In some cases a secondary failure occurred at the stitches, this may be explained by sudden loading of the stiches after first failure of the woven fabric layers. An example of a broken link is presented in Figure 4.
![]()
Figure 4. A broken link example chain tested as number 38 (Table 1), with some remaining intact layers.
3.2. Test Results
As one out of the fifty, a typical test diagram is presented in Figure 5. The load displacement diagram of the tested chains showed a small initial area with low stiffness, followed by a reasonably linear region. Table 1 provides the measured raw breaking forces in order of the test number. The Weibull statistics rank numbers and R values (to be explained in Section 4) are also presented. The number of the broken link is added in the third column. Link numbering was arbitrarily chosen starting counting from driven side of the testing machine.
4. Statistical Treatment
Weibull statistics is often used in structural engineering and material science and was therefore also adopted for the present study. A reason is that it does not comprise negative strength values that are of course impossible and could result from using a Gaussian distribution, so the representation of low strength values (at low failure probabilities e.g. obtained by extrapolation) obtained from a Weibull distribution is expected to be more realistic than obtained from the Gaussian distribution. The original Weibull equation [8] can be written as:
 (1)
(1)
where R is the reliability at load P, and F represents the failure probability. V accounts for effects of volume. For the present case it can be replaced by chain length L. N accounts for the number of chains, as is stated under expression 2 as well, and K for shape effects. Shape effects should be treated with mechanics, rather than statistics, so this facility should be skipped from the equation. Shape effects are anyhow not part of the present consideration. The addition of i to V, K and N refers to the population considered. P0 is a reference strength level, close to the average strength. The exponent m is the so called Weibull modulus. The higher this value, the lower is the strength variability. Ignoring K, Equation (1) can be rewritten for the present chains as:
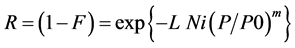 (2)
(2)
where L is the effective span length of one chain and N is the number of chains. Accordingly, when a number Ni of chains with length L is considered, the total chain length considered Li is:
 (3)
(3)
Equation (3) can be substituted in Equation (2), reducing the first part between the brackets to total chain length only. A Graphical representation of a Weibull distribution can be made by plotting the natural logarithm of minus the natural logarithm of R on the vertical axis and the natural logarithm of the measured load P on the horizontal axis. R is than calculated from the rank number n (from strongest to weakest) of the rest result and the number of tests N according to:
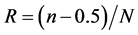 (4)
(4)
![]()
Figure 5. Example of one load displacement diagram of the test on chain test number 38 (Table 1).
![]()
Table 1. Tensile test results on chains.
Equation (4) is identical to Weibull’s original work. It can be understood such that the “reliability space” is divided in N blocks with rank n. The R value is placed in the center of each nth-block, adding −0.5 provides that placement in the middle. A graphical representation is made as a first consideration for all as measured data from Table 1, and presented in Figure 6. The axis values in Figure 6 are chosen such that an extrapolation to R = 0.999999 is visible. In other words a failure probability F of one out of a million can be seen. Of course such a far extrapolation is not accurate anymore. It is just a reasonably probable expectation for the strength at very low failure probabilities. It should be noted that none of the chain links broke at the interface with the steel pin. All breaks were at link-link interfaces. Thus the two link-steel interfaces were such strong (due to the large radius of the oval pin of 35 mm), that they were not representative and equivalent to not tested one. Two not tested interfaces are equivalent to one link (as each link comprises two interfaces). So the plot in Figure 6 is not representative for a 6-link chain of 0.6 meter, but for a 5-link chain that is 0.5 meter, so L = 0.5. The fit of the line to the data, is just the linear fit from the MS Excel program. The rounded values for this situation are: P0 = 216.5 kN and m = 22.6. Figure 6 in a mathematical representation is presented below:
 (for 0.5 meter chains). (5)
(for 0.5 meter chains). (5)
It can be seen in Figure 6 that the data points can reasonably fitted with a straight line, so indeed the data are reasonably be described with the Weibull distribution. The fit to the straight line is not perfect. This is normal for such plots. A perfect fit would be an extreme coincidence. Nevertheless, it is interesting to compare the Weibull fit to another commonly used fit, the normal distribution. The lower tail of the data set is most interesting, because this comprises the higher reliabilities, so this is considered only. Table 2 presents the four lower data sets, together with the R-values from Table 1 as experimental values and the calculated R-value according to Equation (5) and additionally according to a normal distribution with the average of 217.9 kN, and the standard deviation of 11.7 kN. It can be observed in Table 2, that the Weibull fit agrees somewhat better to the experimental values, so it should be preferred indeed.
Ni is the number of chains of 0.5 meter. Indeed, inserting for Ni = 1 Million as an example for P = 121 kN, the resulting reliability R = 0.38. So suggesting a considerable chance of failure of one from those million chains, occurring at P = 121 kN. Another way of interpretation, is that a million times a chain of 0.5 meter, implies a total chain length of 500 km. So also a 500 km long chain, loaded with P = 121 kN has a reliability of 0.38. Loading of such a 500 km total chain length with the certified WLL = 100 kN still implies a reliability R = 0.987.
![]()
Figure 6. Weibull plot of the as measured data from Table 1, representative for chains of 0.5 meter.
![]()
Table 2. Comparison of reliabilities for a normal and Weibull distribution to experimental values.
An alternative consideration can be made after studying Table 1. It turns out that the number of breaks in the first and last outer links is relatively high. This in spite of the fact that these outer links comprise one critical textile-textile interface only instead of two textile-textile interfaces for the adjacent links. Also the average breaking force is lower, when fracture occurred at outer link 1 or at outer link 6. So the outer links are another weaker sub population. It was demonstrated in [9] that mixing different sub populations causes a non-represent- ative reduction of the Weibull exponent, so a seemingly increasing scatter. Table 3 presents strength data and failure numbers for the individual links. Indeed the outer link fractures occur at a lower average load. Moreover, Table 1 shows that the five lowest breaking forces (Test 15, 9, 4, 24 and 12 in order of decreasing strength) belong to this affected sub population. The strength values in the non-affected sub population are all well above MBL > 200 kN. The earlier fracture of the outer links can be explained by additional tension, introduced by the thickness of 30 mm of the pin at the opposite side of the fractured links. This thickness being larger than the link width under load causes a small V-shape for the two sides of the link, they are not parallel anymore. The V-shape points towards the critical link-link interface. This may cause a slight increase of the stress concentration at that interface, so earlier fracture may occur. The 30 mm thickness of the pin was chosen for making it sufficiently strong and especially to prevent fracture at the pin-link interface. In retrospect, a smaller width may be a better choice. It appears obvious that the original dataset is a structured data set that consists of two sub populations.
Removal of the first and last link fractures from the data set, so removal of a non-representative sub population can be explored. The consequence of that segmentation is, that chains of 0.4 meter are remaining, so L = 0.4. It may be argued that removing lower values from the original data set causes an artificial non-realistic improvement. However, the removed links are not chosen based on their lower fracture load, but based on their position (the lower fracture load is only used for recognizing the non-representative positions). Moreover, the removal effect itself is compensated by correcting for a lower representative chain length in the Weibull equation. Also in practice a 16mm pin is used for load transfer into steel hooks. An additional argument for the segmentation is that the unfavorable interface fracture implies that the remaining interface of the removed links will have a fracture force, larger than the measured fracture force that was limited by the broken outer link. So potential high fracture loads belonging to the sub population of the considered central chain part were omitted, and the consideration may even be conservative. Summarizing, removal of the outer link fractures from the data set is defendable for providing a description of intrinsic chain behavior without any external outside world influence like end connections. Performing a Weibull fit on the remaining data for the central part yields:
 (for 0.4 meter chains, no end connections). (6)
(for 0.4 meter chains, no end connections). (6)
This new Equation (6) shows a higher Weibull exponent indeed as compared to Equation (5). The index i has been replaced by index j in order to indicate a different population. It may be explored by inserting some numbers and comparing the result with the result of Equation (5). A length of 500 km chain is equivalent to Nj = 1,250,000. For a load of P = 121 kN, the reliability is R = 0.95, so considerably larger than according to Equation (5) representing the mixed population. A reliability of R = 0.38 as obtained with Equation (5) for a load of P = 121 kN for the mixed population, requires a load of P = 134.5 kN on the population of the central links according to Equation (6). Indeed this is a more attractive value than according to the first consideration, but not largely different (134.5 kN is only about 10% larger than 121 kN). The reliability according to Equation (6) for 500 km total chain length at WLL = 100 kN, now is R = 0.9997, so very close to R = 1. Figure 7 presents the data of the central links in a Weibull plot, compared to the plot of the outer links. Again a linear fit appears reasonable. However, the lower end of the plot of the central links suggest a steeper line in this area (more favorable
![]()
Table 3. Number of fractures and average fracture load per link.
![]()
Figure 7. Weibull plots of data for the central links, and outer links as separate sub populations.
for low risk extrapolations). The main part of this steeper trend is set by three data points only. So, this deviation may still be judged coincidental and a linear fit for extrapolation is still adopted as a reasonable procedure.
5. Discussions and Conclusions
Weibull statistics is applied on a set of 50 tensile tests on novel light weight synthetic link chains made from UHMWPE fiber instead of traditional steel wire. During tensile testing, a slight adverse measuring effect of the connection to the tensile test equipment became apparent. The effect was not found at the end termination itself, but at the opposite site of the link-machine interface. It can be explained by the deformation of the end links due to the thickness of the required connection pin. Two Weibull distributions were created that are used for extrapolation, one by fitting the data sets to all 50 results and one by fitting to a dataset without the outer links attached to the test equipment. The latter showed a higher Weibull exponent. The data sets were used for extrapolation to low failure risks or to very long total chain lengths (so the total length of a number of chains). The result is that the reliability of the chains is high, if the Work Load Limit WLL = 100 kN is respected. The extrapolations of the central part represent the intrinsic chain behavior. Additional effects like connection effects are excluded. So effects as caused by end connections and possible hooks are excluded. Of course such effects are relevant in practice, but beyond the scope of the present study. The present study indicates that the intrinsic consistency of chain properties is highly sufficient for safe use. Table 4 presents a number of calculated failure probability values for chains of different length, loaded at WLL according to both considerations: the mixed population and the population with excluded outer links.
![]()
Table 4. Examples of calculated reliabilities at a WLL of 100 kN, for various total chain lengths, using two different considerations.
Obviously, the failure probabilities remain low, so the reliabilities at WLL (100 kN) remain high, even for very long total chain lengths (5000 km). It was mentioned before that this far extrapolation is not an accurate prediction, but rather a reasonable expectation. Moreover, all chains are loaded at WLL = 100 kN, before leaving the factory, so fractures at WLL would occur before chains become in use. On the other hands, chains with a slightly larger strength than 100 kN would become in use. It is beyond the scope of this paper to speculate on the consequences of these effects, because reliability at 100 kN is high anyhow, even for large total chain lengths. It can be observed in Table 4 that the failure probabilities for the central link population and the mixed population become more different for extreme total chain lengths (or numbers, the total length is the important parameter). The failure probability of the central link population remains very close to 0, even for 5000 km total chain length. So the reliability will remain close to 1.
NOTES
![]()
*Corresponding author.