Prediction of Burst Pressure of a Radial Truck Tire Using Finite Element Analysis ()
Received 7 April 2016; accepted 10 May 2016; published 13 May 2016

1. Introduction
In general, a tire must be sufficiently rigid to withstand various loading conditions and ensure different functions such as sufficient traction for driving and braking, steering control and stability or as cushion of road irregularities. Tire durability due to large local loading, stiffness discontinuities, and production flaws is frequently related to the fracture of tire components such as belt edge separation, ply turn-up separation, or lug cracking in radial truck tire [1] - [4] . An influence factor on fracture and fatigue behaviors of the tire component is the key to improve durability and assess lifetime of the radial truck tire [5] .
Bead area separation in passenger tires has been fairly uncommon since the middle to late 1990s. In light truck-type tires, especially load range D and E sizes, bead area separation is unusual but not rare and remains small in number compared to the number of belt separations. Especially, broken beads are uncommon but can fail in the following instances [6] : a mismatch of the tire and the wheel/improper mounting methods or obstructions causing a “hang-up” of the bead in the wheel well/shipping damage to the bead area/tires mounted with kinked beads, indicating prior bead damage/insufficient bead strength, incorrect wire yield strength, incorrect wire type (ultimate tensile), or incorrect wire diameter/incorrect (low) bead winding diameter and/or an incorrect (high) bead seat diameter. During the investigation of a bead core break, the wires should be analyzed under magnification to determine the type of break as shown in Figure 1.
Destructive tests such as the application of burst pressure, high-speed free rotation, and plunger energy are sometimes performed on new tires to ascertain their ultimate strengths [7] . These tests are used for the qualification of a new tire design as well as to determine the extent to which the tire can be loaded beyond the manufacturer’s recommended service conditions before failing.
Bolarinwa and Olatunbosun [8] have studied that a numerical approach for modeling tire burst phenomenon under severe inflation pressure has been presented by making use of a commercial FE code, which allows the modelling of the tire burst phenomenon, based on the ultimate strengths of the constituent reinforcement materials.
More recently, Michel et al. [9] performed tire burst phenomenon and rupture of a typical truck tire bead design. Tire burst pressure can be predicted by a complex finite element modeling by identifying the pressure at which the maximal plastic strain of steel bead wires is reached. However, an axisymmetric finite element tire model, which allows the modeling of the tire burst phenomenon, based on the cord breaking force of the constituent reinforcement materials, has not yet been addressed.
The purpose of the present study is to develop the finite element modeling for the prediction of the burst pressure of radial truck tires. The tire burst pressure, under this extreme loading condition, can be predicted by identifying the pressure at which the cord breaking force of the composite materials is attained. In order to determine the burst pressure of a radial truck tire, an axisymmetric finite element model has been developed using a commercial FE code [10] . The model is able to well predict the tire burst pressure by identifying the pressure at which the break force of steel bead wires is reached. A summary of the results obtained from this model for a radial truck tire 12R22.5 is presented together with a study of the effect of some tire bead design parameters on the tire burst pressure.
![]()
Figure 1. Tensile breaks of the bead wires [6] .
2. Finite Element Model
2.1. Tire Model
A tire usually consists of several rubber components, each of which is designed to contribute to some particular factors for tire performance in addition to several cords and rubber composites. These components play a role in maintaining the stiffness and strength required in a tire. Figure 2 shows the finite element mesh on the general structure of a radial truck tire with a size of 12R22.5 found in radial truck and bus tires, where the roles of tire components are well described in a book by Clark [11] . It consists of a radial carcass ply, four belt plies, steel chafer, bead wires, and several rubber components. Figure 2 shows a two-dimensional axisymmetric finite element mesh in a section, in which 4-node quadrilateral and 3-node triangular elements are used.
2.2. Material Model
The material composition of most tires is distinguished largely into the fiber-reinforced rubber (FRR) parts and the remaining pure rubber part. The FRR parts of the tire model considered here are composed of a single-ply polyester carcass, four steel belt layers, and several steel bead cords. Since the FRR parts are in the highly complex structure, their material models are chosen based on the goal of the numerical simulation. When FRR parts are modeled using finite element analysis, the physical properties of the rubber and cords are combined to yield the resulting physical behavior of the FRR [12] - [15] , the internal cords are modelled using beam elements [16] or using rebar elements [17] - [23] . Studies that have modeled belts based on a single physical behavior have defined the behavior using isotropic elasticity [12] , hyperelasticity [24] , the Halpin-Tsai composite equation [13] , or theoretically derived belt constitutive equations [14] [15] .
Rubbers except for the FRR parts are modeled by the penalized first-order Mooney-Rivlin model in which the strain density function is defined [13] .
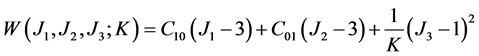 . (1)
. (1)
where Ji are the invariants of the Green-Lagrangian strain tensor and C10 and C01 are the rubber material constants determined from the experiment. On the other hand, K is a sort of penalty parameter controlling the rubber incompressibility. The shear modulus τ and the bulk modulus k of rubber are related as 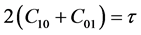 and
and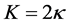 , from which one can easily obtain the following relation for Poisson’s relation:
, from which one can easily obtain the following relation for Poisson’s relation:
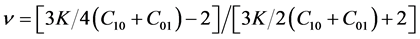 . It is clear that the incompressibility of rubber is asymptotically enforced as the penalty parameter approaches infinity, but the choice of K near 100 is usually recommended for the stable transient dynamic response with the reasonable time step size.
. It is clear that the incompressibility of rubber is asymptotically enforced as the penalty parameter approaches infinity, but the choice of K near 100 is usually recommended for the stable transient dynamic response with the reasonable time step size.
![]()
Figure 2. A 2-D section mesh of 12R22.5 tire.
2.3. Composite Model
Structural tire analysis is often performed using the cured tire geometry as the reference configuration for the finite element model. However, the cord geometry is more conveniently specified with respect to the “green” or uncured, tire configuration. The tire lift equation provides mapping from the uncured geometry to the cured geometry as shown Figure 3. This study can specify the spacing and orientation of the rebar cords with respect to the uncured configuration and let Abaqus [10] map these properties to the reference configuration of the cured tire. Using a cylindrical coordinate system, the spacing, s, and angular orientation, α, in the cured tire are obtained from
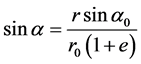 ,
, 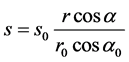 , (2)
, (2)
where r is the position of the rebar along the radial direction in the cured geometry, r0 is the position of the rebar in the uncured geometry, s0 is the spacing in the uncured geometry, α0is the angle measured with respect to the projected local 1-direction in the uncured geometry, and e is the cord extension ratio. A local cylindrical coordinate system must be defined for the rebar if the rebar is associated with three-dimensional elements.
2.4. Bead Model
In order to predict the tire burst pressure by identifying the pressure at which the cord breaking force of steel bead wires is reached, the rebar element is used. Figure 4 shows the finite element mesh in a section on the solid or rebar element of bead wire. In general, in order to predict the performance of the tire, the bead is used for the solid element as shown Figure 4(a). However, this study uses the rebar element provided by ABAQUS [10]
![]()
Figure 3. Mapping between uncured and cured tire rebar geometry [10] . (a) Uncured geometry; (b) Cured geometry.
![]()
Figure 4. The finite element modeling of bead wire in a section. (a) Solid element; (b) Rebar element.
because it must calculate the cord tension of bead wire as shown in Figure 4(b). One wire of bead is modeled as one element.
2.5. Boundary Condition
To simulate the contact between the tire and the rim, the general purpose interface is defined between a tire slave surface and a rigid body surface of the rim. The inner and outer rim profiles are both modeled by axisymmetric rigid surfaces. Contact with friction is considered between the tire and the rim. The coefficient of friction is assumed to be 0.3 or 0.5. No other interface is used to model the contact between the rubber matrix and the beads or between the rubber matrix and the different layers, such as carcass ply, belt, bead wrap and steel chafer. The effect of the change of friction coefficient on the tire burst pressure is discussed.
3. Tire Burst Pressure Analysis
The tire burst pressure, under this extreme loading condition, can be predicted by identifying the pressure at which the cord breaking force of the composite materials is attained. In addition, the plot of the cord tension of rebar against the inflation pressure reveals their responses to pressure loading leading to tire burst.
3.1. Cord Tension Analysis
The tire model’s response to an extremely large, but progressively applied, inflation pressure is simulated by inflating the tire up to a limit of 400 psi inflation pressure, representing a 333 per cent increase in the tire’s rated inflation pressure (120 psi). The resulting plot of the deformed geometry with the different bead modeling at a pressure of 120 psi is shown in Figure 5. It is found that the deformation of the rebar element is greater than the solid element. Because the bead part with solid element has very small deformation, the rebar element is more effective for the optimized bead design using finite element analysis. Figure 6 shows the deformed shape of bead part as an inflation pressure up to 400 psi increases. While the inflation pressure is increased to 400 psi, the
![]()
Figure 5. Deformed shape at inflation pressure 120 psi. (a) Solid element; (b) Rebar element.
![]()
Figure 6. Deformed shape of bead part. (a) 120 psi; (b) 200 psi; (c) 400 psi.
excessive deformation of tire bead part is generated, but there is no convergence problem. Figure 7 shows the cord tension in each rebar layer as the inflation pressure increases. In order to determine the pressure at which the cord tension of the tire reinforcements is achieved, the breaking force of the cords, modelled with rebar elements, are used, as shown in Table 1. The steel components inside radial truck tire are carcass ply, belts with 4 layers, chafer, and bead. Because the wrap around the bead is polyester, the breaking force of the wrap is low. As the inflation pressure increases, the cord tension of bead wire greatly increases as shown in Figure 7. It is found that the bead wire among the various layer modelled the rebar element breaks off first in the radial truck tire. Figure 8 shows a flow diagram of the finite element analysis procedure.
![]()
Figure 7. Reinforcement material’s cord tension versus inflation pressure.
![]()
Figure 8. Flow chart for finite element analysis.
![]()
Table 1. Cord breaking forces of composite materials.
The inflation pressure of about 300 psi, at which the rebar element breaks, is assumed to correspond to the tire model burst pressure. This proves to be reasonably close to the burst pressure of 264.85 psi [9] , obtained in tests on similar radial truck tires, though from another manufacturer. And also, the tire burst pressure obtained in the hydrostatic burst test is 251.8 psi. In order to determine the tire strength when inflated beyond the maximum pressure recommended by the manufacturer, a hydrostatic burst test is performed on a new 12R22.5 truck tire. Pressurization with water is homogeneous and accurate, and it is the safest method to determine the integrity of any type of container [25] . Because of the incompressibility of water, energy stored inside the tire is indeed much lower than air inflated. The experimental setup and tire failure used for the hydrostatic burst test is illustrated in Figure 9.
The bead wires undergo plastic deformation until failure. However, this study is not considered the plastic strain of steel cord because the rebar element provided by ABAQUS [10] cannot reflect the plastic zone. Even though the plastic deformation in the simulation results is neglected, the current model can be improved in order to predict tire burst pressure. The tire burst pressure can be predicted by a finite element modeling by identifying the pressure at which the breaking force of steel bead wires is reached.
3.2. Parametric Study
An important feature of the finite element tire model is that it provides a cost-effective means of carrying out parametric studies on the tire so as to optimize desired performance output. As a result of this, the bead properties can be optimized to achieve a target burst pressure. The main effect of changing the cylindrical diameter of bead and the wire number of the bead design on the tire burst pressure will be investigated using an organized approach popularly referred to as the Design of Experiment (DOE) [26] [27] .
Table 2 and Figure 10 show the design parameters, such as the cylindrical diameter and wire number of bead wires, for a severe service condition such as burst pressure. Typically, based on the result of the parametric studies,
![]()
Figure 9. The hydrostatic burst test. (a) Experimental setup; (b) Tire failure.
![]()
Figure 10. Tire burst pressure with respect to bead design. (a) 51; (b) 57; (c) 60.
![]()
Table 2. Design with the different bead structure.
burst pressure can be taken to be dependent on the bead diameter and the wire number. In order to select the optimized design of the bead wire, the structure of bead wire consists of 51 (8 + 9 + 10 + 9 + 8 + 7), 57 (8 + 9 + 10 + 11 + 10 + 9), and 60 (9 + 10 + 11 + 11 + 10 + 9). From this table of properties, a matrix of nine experiments or simulations and a resulting output burst pressure are generated. Figure 11 shows the simulation results of the tire burst pressure with respect to bead design. The friction coefficient between the tire and the rim is applied to 0.3 or 0.5. It is found that the effect of friction coefficient on the tire burst pressure is small. From the simulation results shown in Figure 11, the tire burst pressure increases as the wire number increases and the effect of the cylindrical diameter of bead has the least effect.
The correlation between simulation and test is shown in Figure 12. The horizontal axis is the predicted tire burst pressure, and on the vertical axis is the test result. In this Figure 12, the FEA-based burst pressure model of a radial truck tire can be used as a pass-or-fail screening tool for the tire bead designs related to the cylindrical diameter of bead and wire number. Figure 13 shows the graphical interpretation to the DOE for the tire burst pressure with respect to bead design. Because the bead design of Version 9 has the highest burst pressure, it is the strongest design for a tire burst. It is found that the design parameter on the effect of bead design on the tire burst pressure is the number of bead wires as shown Pareto chart of the normalized effect in Figure 13.
4. Conclusion
The finite element modeling technique is employed for the calculation of the burst pressure of a radial truck tire, based on the static loading analysis. The high internal pressure produces high circumferential tension in the bead wire. The cord tension can no longer be sustained resulting in a chain reaction and consequently leading to the burst. In order to predict of burst pressure of a radial truck tire, an axisymmetric finite element model is used.
![]()
Figure 11. Tire burst pressure with respect to bead design.
![]()
Figure 12. Correlation between FEA and TEST. (a) μ = 0.3; (b) μ = 0.5.
![]()
Figure 13. Graphical interpretation to the DOE for the burst pressure sensitivity study. (a) TEST; (b) μ = 0.3; (c) μ = 0.5.
The finite element modeling with the rebar element on the bead wire of a radial truck tire is able to well predict the tire burst pressure identifying the pressure at which the breaking force of steel bead wires is reached. Because the simulation results and those obtained experimentally are in good agreement, it offers better understanding of the tire failure mechanism under inflation pressure, revealing the behavior of tire reinforcements leading to failure. Finally, the bead model developed in this study shows significant flexibility in being used as a radial truck tire design sensitivity tool for optimizing design parameters for a severe service condition such as burst pressure. It is found that the prediction of tire burst pressure using a finite element method will be useful for the reliable bead design of a radial truck tire.
Acknowledgements
The present study was supported by the Center for Environmentally Friendly Vehicles (CEFV) under the project “Development of the eco-friendly tire for reduction of carbon dioxide and tire wear particles” through the Ministry of Environment (ME, Republic of Korea).