Based on Adaptive Backstepping Error Control for Permanent Magnet Synchronous Motor ()
Received 2 February 2016; accepted 30 April 2016; published 3 May 2016

1. Introduction
Research on PMSM has been going on for many years due to the fact that they have many advantages over the conventional internal combustion engine vehicle, such as independence from petroleum, reliability and quiet [1] - [3] .
However there appear phenomena of chaos in PMSM when PMSM in turn on or turn off [4] [5] . Chaos of PMSM is harmful. Chaos can degrade performance of PMSM, even destroy PMSM and restrict the operating range of numerous electrical and mechanical devices. The high performance of PMSM depends on the absence of chaos so it is important for PMSM to control chaos [6] [7] . Due to the fact that PMSM is multivariable, nonlinear and strongly coupled plant, controlling chaos of PMSM is very difficult [8] .
With the development of theory of chaos, there are many methods for control and analysis chaotic system [9] [10] . For example, the OGY is a basic methodology for controlling chaos. At the same time, there are variable structure control [11] , entrainment and migration control, nonlinear feedback control [12] , total sliding-mode control [13] and the backstepping nonlinear control, self-constructing fuzzy neural network speed control [14] , dither chaos [15] , hybrid control [16] and passivity control [17] .
Various ways and techniques had been successfully used to control or suppress chaos in PMSM. For example, in 2009, M. Zribi et al. proposed to control chaos in PMSM by instantaneous Lyapunov exponent control algorithm [18] . In 2010, D. Li et al. proposed impulsive control for PMSM [19] . In 2010, S. C. Chang proposed synchronous and control chaos in a PMSM [20] . In 2011, J. Yu et al. proposed backstepping control for the chaotic permanent magnet synchronous motor drive system [21] . In 2011, S. C. Chang et al. proposed dither signal to quenching chaos of a permanent magnet synchronous motor in electric vehicles [22] . However, these methods appear oscillation in course of control chaos in PMSM which has an effect on practical application.
In this paper, a scheme is proposed to suppress oscillation in course of control chaos in PMSM. An error control item is added in the each step virtual control design which has control effect of unknown dynamical error on system. This scheme can gain more smoothly chaotic stabilization process and overcome oscillation in course of control chaos in PMSM. At the same time, all the signals in the system are bounded which based on Lyapunov function. This scheme has better transient response by simulation.
2. Problem Formulation
The dynamics PMSM, which model base on d-q axis, can be described as follows:
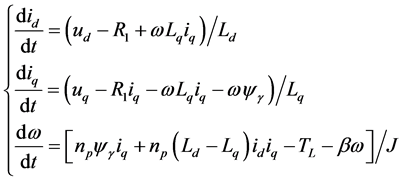 (1)
(1)
where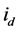 ,
,  and
and 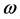 are state variables, which denote d-axis stator current, q-axis stator current and rotor angular speed respectively;
are state variables, which denote d-axis stator current, q-axis stator current and rotor angular speed respectively;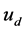 ,
, 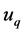 and
and  are d-axis external voltage, q-axis external voltage and external torque;
are d-axis external voltage, q-axis external voltage and external torque; 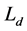 and
and 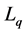 are d-axis stator inductance and q-axis stator inductance.
are d-axis stator inductance and q-axis stator inductance. 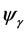 is permanent magnet flues,
is permanent magnet flues,  is stator winding resistance,
is stator winding resistance, 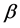 is the viscous damping coefficient, J is rotor rotational inertia,
is the viscous damping coefficient, J is rotor rotational inertia, 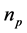 is the number of pole-pairs,
is the number of pole-pairs, 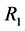 ,
, 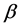 , J,
, J, ![]() ,
, ![]() ,
, ![]() are all positive. Applying transformation form,
are all positive. Applying transformation form, ![]() , and a time scaling transformation,
, and a time scaling transformation, ![]() , where
, where
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
The system (1) can be changed into nondimensionalized form as follows:
![]() (2)
(2)
where
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,![]() .
.
System (2) is smooth air-gap when![]() . In order to describe conveniently, assuming
. In order to describe conveniently, assuming![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . The model can be simplified as follows:
. The model can be simplified as follows:
![]() (3)
(3)
Now, for model of PMSM of smooth air-gap (3), research motor without external force which can be considered PMSM no-load running and power fail interrupt, namely,![]() . The system (3) can be shows as follows:
. The system (3) can be shows as follows:
![]() (4)
(4)
the parameters value of system (4), ![]() and
and![]() , can effect on chaotic motion of PMSM greatly. Theoretically, there are many values of
, can effect on chaotic motion of PMSM greatly. Theoretically, there are many values of ![]() and
and ![]() which can cause chaos occurred in system (4). For system (4),
which can cause chaos occurred in system (4). For system (4),
![]() .
.
Due to![]() ,
, ![]() , so the system (4) is dissipative system base on dissipation theory. System (4) is chaos when
, so the system (4) is dissipative system base on dissipation theory. System (4) is chaos when ![]() and
and ![]() base on above analysis [22] . The system (4) have three equilibrium point:
base on above analysis [22] . The system (4) have three equilibrium point:![]() ,
, ![]() ,
,![]() .
.
3. Theory and Method
Set
![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
So system (4) can be change as follows:
![]() (5)
(5)
To realize stability of system (4), we may add controller to the third equation of system (4), system (4) can be changed as follows:
![]() (6)
(6)
Definite three error variables:
![]() (7)
(7)
Step 1: Base on system (7), the first derivative of ![]() is
is
![]() . (8)
. (8)
Choose the Lyapunov function candidate as:
![]() , (9)
, (9)
then the time derivative of ![]() is computed,
is computed,
![]() . (10)
. (10)
The virtual control ![]() is constructed as
is constructed as
![]() , (11)
, (11)
where ![]() and
and ![]() are control parameters,
are control parameters, ![]() ,
, ![]() , substituting Equation (11) into Equation
, substituting Equation (11) into Equation
(10) that
![]() . (12)
. (12)
Step 2: Derivative of![]() , we have equation,
, we have equation,
![]() , (13)
, (13)
substituting Equation. (8) into Equation (13), the Equation (13) expression is given by
![]() (14)
(14)
where![]() ,
, ![]() are
are![]() ,
, ![]() estimated value,
estimated value, ![]() ,
, ![]() ,
, ![]() and
and ![]() are parameters estimation error.
are parameters estimation error.
Choose the Lyapunov function as follows,
![]() ,
,
the time derivative of ![]() is given by
is given by
![]() (15)
(15)
Choose parameters adaptive rule:
![]() (16)
(16)
where![]() .
.
Construct the virtual control ![]() as
as
![]() , (17)
, (17)
where![]() ,
, ![]() is a control parameter, substituting Equation (16) and Equation (17) into Equation (15), equation Equntion (15) can be obtained as follows,
is a control parameter, substituting Equation (16) and Equation (17) into Equation (15), equation Equntion (15) can be obtained as follows,
![]() . (18)
. (18)
Base on Young inequality [21] , inequality (19) can be obtained as follows
![]() (19)
(19)
so a straightforward calculation produces the following inequality
![]() (20)
(20)
Step 3: Derivative of ![]() results in the following differential equation,
results in the following differential equation,
![]() (21)
(21)
choose![]() , Equation (21) can be written as follows,
, Equation (21) can be written as follows,
![]() , (22)
, (22)
choose the Lyapunov function candidate as
![]() . (23)
. (23)
The time derivative of ![]() is
is
![]() (24)
(24)
setting
![]() (25)
(25)
substituting Equation (25) into Equation (24), we have the following equation.
![]() . (26)
. (26)
Similar to![]() ,
,
![]() , (27)
, (27)
set
![]()
![]() ,
,
inequality can be obtained as follows,
![]() . (28)
. (28)
4. Stability Analysis
Theorem 1. Consider chaotic system (6) and parameter identification (16), for bounded initial conditions, the following conclusion was established:
(1) All the signals the consistent bounded in chaos system, state error ![]() and parameter estimates error
and parameter estimates error![]() ,
, ![]() eventually converge to bounded sets:
eventually converge to bounded sets:
![]() .
.
(2) Reasonable choosing parameters m, n and![]() , state of chaotic system
, state of chaotic system![]() ,
, ![]() and
and ![]() can be stability in bounded point neighborhood
can be stability in bounded point neighborhood![]() .
.
Proof: Choose Laypunov function![]() , by Equation (28) can be obtained as follows,
, by Equation (28) can be obtained as follows,
![]() . (29)
. (29)
Equation (29) above both sides by the same![]() , inequality can be obtained as follows
, inequality can be obtained as follows
![]() ,
,
namely
![]() , (30)
, (30)
integral of formulas (30) in![]() ,
,
![]() . (31)
. (31)
For bounded initial conditions![]() , we can draw a conclusion that
, we can draw a conclusion that ![]() is bounded base on theorem of Laypunov. We can get
is bounded base on theorem of Laypunov. We can get![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() consistent bounded to inequality (28). Base on virtual control
consistent bounded to inequality (28). Base on virtual control![]() ,
, ![]() ,
, ![]() and
and ![]() are all bounded. Control input u is bounded base on Equation (25), so all the signals in chaotic system are consistent bounded.
are all bounded. Control input u is bounded base on Equation (25), so all the signals in chaotic system are consistent bounded.
When![]() ,
,
![]() .
.
So state error ![]() and parameter estimation errors
and parameter estimation errors![]() ,
, ![]() eventually converge to a bounded set
eventually converge to a bounded set
![]() .
.
From inequality (31), inequality can be obtained as follows
![]() , (32)
, (32)
where![]() ,
, ![]() ,
, ![]() setting
setting ![]() base on Equation (32) inequality can be obtained as follows,
base on Equation (32) inequality can be obtained as follows,
![]() . (33)
. (33)
Given constant![]() , existing
, existing![]() , for all
, for all![]() , error
, error ![]() satisfy
satisfy![]() . We reasonable choose values of m, n and
. We reasonable choose values of m, n and ![]() which lead to the value of
which lead to the value of ![]() can be decreased. So,
can be decreased. So, ![]() may eventually converge to a stable in bounded neighborhood
may eventually converge to a stable in bounded neighborhood![]() . Accordingly to Equation (10) and Equation (17),
. Accordingly to Equation (10) and Equation (17), ![]() ,
, ![]() and
and ![]() are chosen smaller constant,
are chosen smaller constant, ![]() can be stabled in bounded neighborhood
can be stabled in bounded neighborhood![]() . So system (5) can be stable in bounded neighborhood
. So system (5) can be stable in bounded neighborhood![]() .
.
5. Simulation Results
Choose![]() ,
, ![]() , the system (4) is chaos. Let
, the system (4) is chaos. Let ![]() due to
due to![]() ,
, ![]() ,
, ![]() ,
,![]() . Figure 1 shows the synchronization errors. From Figure 1, we can see that the proposed controller and the parameters update law are effective.
. Figure 1 shows the synchronization errors. From Figure 1, we can see that the proposed controller and the parameters update law are effective.
6. Conclusion
This paper puts forward error control for permanent magnet synchronous motor with uncertain parameter based on adaptive backstepping which can effectively eliminate oscillation during the course of control chaos in PMSM. An error control item is added in the each step virtual control design which has control effect of unknown dynamical error on system. This scheme can gain more smoothly chaotic stabilization process. At the same time, all the signals in the system are bounded base on Lyapunov function. This scheme has better transient response by simulation.
Acknowledgements
This research is supported by the Sichuan Province Natural Science Foundation of China (Nos. 2014GZX0008, 2016JY0179), the Innovation Group Build Plan for the Universities in Sichuan (No. 15TD0024), the High-level Innovative Talents Plan of Sichuan University of Science and Engineering (2014), the Talents Project of Sichuan University of Science and Engineering (No. 2015RC50), the Cultivation Project of Sichuan University of Science and Engineering (Nos. 2012PY18, 2012PY19, 2012PY20), and the Project of Artificial Intelligence Key Laboratory of Sichuan Province (Nos. 2011RZY05, 2014RYY05, 2015RYY01).
NOTES
![]()
*Corresponding author.