Global Convergence of Curve Search Methods for Unconstrained Optimization

Zhiwei Xu¹, Yongning Tang², Zhen-Jun Shi³

¹Computer and Information Science, University of Michigan, Dearborn, MI, USA.
²School of Information Technology, Illinois State University, Normal, IL, USA.
³Mathematics and Computer Science, Central State University, Wilberforce, OH, USA.

DOI: 10.4236/am.2016.77066                

Abstract

In this paper we propose a new family of curve search methods for unconstrained optimization problems, which are based on searching a new iterate along a curve through the current iterate at each iteration, while line search methods are based on finding a new iterate on a line starting from the current iterate at each iteration. The global convergence and linear convergence rate of these curve search methods are investigated under some mild conditions. Numerical results show that some curve search methods are stable and effective in solving some large scale minimization problems.

Keywords

Unconstrained Optimization, Curve Search Method, Global Convergence, Convergence Rate

Received 20 December 2015; accepted 25 April 2016; published 28 April 2016

1. Introduction

Line search method is an important and mature technique in solving an unconstrained minimization problem

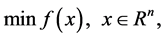(1)

where 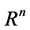is an n-dimensional Euclidean space and 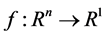is a continuously differentiable function. It takes the form

(2)

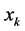where is a descent direction of at and 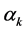is a step size to satisfy the descent condition

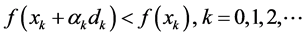(3)

One hopes that 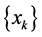generated by line search method converges to the minimizer 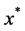of (1) in some sense. Let be the current iterate. We denote 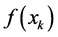by, by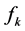, and by, respectively.

At the k-th iteration of line search methods, one first chooses a search direction and then seeks a step size along the search direction and completes one iteration (see [1] ). The search direction is generally required to satisfy

(4)

which guarantees that is a descent direction of at (e.g. [2] [3] ). In order to guarantee the global convergence, we sometimes require to satisfy the sufficient descent condition

(5)

where is a constant. Moreover, the angle testing condition is commonly used in proving the global convergence of related line search methods, that is

(6)

where.

In line search methods we try to find an to reduce over the ray at the k- th iteration, while curve search method is to define the next iterate on the curve

where and means that is continuously differentiable on. It is obvious that line search method is a special one of curve search methods. In other words, curve search method is a generalization of line search methods.

McCormick [4] and Israel Zang [5] proposed an arc method for mathematical programming, which is actually a special one of curve search methods. Similarly as in line search methods, how to choose a curve at each iteration is the key to using curve search methods.

Botsaris [6] - [9] studied differential gradient method (abbreviated as ODE method) for unconstrained minimi- zation problems. It is required to solve differential equations at the k-th iteration

or to solve

where and The ODE method has been investigated by many researchers (e.g. [10] - [14] ) and is essentially a curve search method.

However, it is required to solve some initial-value problems of ordinary differential equations to define the curves in ODE methods. Some other curve search methods with memory gradient have also been investigated and been proved to be a kind of promising methods for large-scale unconstrained optimization problems (see [15] [16] ). Other literature on curve search methods have appeared in the literature [17] - [19] . To the best of our knowledge, the unified form of curve search methods has rarely been studied in present literature. It is necessary to study the general scheme of curve search methods and its global convergence.

In this paper we present a new family of curve search methods for unconstrained minimization problems and prove their global convergence and linear convergence rate under some mild conditions. These method are based on searching a new iterate along a curve at each iteration, while line search methods are based on finding a new iterate on a line starting from the current iterate at each iteration. Many curve search rules proposed in the paper can guarantee the global convergence and linear convergence rate of these curve search methods. Some implementable version of curve search methods are presented and numerical results show that some curve search methods are stable, useful and efficient in solving large scale minimization problems.

The rest of this paper is organized as follows. In the next section we describe the curve search methods. In Sections 3 and 4 we analyze its global convergence and linear convergence rate respectively. In Section 5 we report some techniques for choosing the curves and conduct some numerical experiments. And finally some conclusion remarks are given in Section 6.

2. Curve Search Method

We first assume that

(H1). The objective function is continuously differentiable on and the level set

is bounded, where is given.

(H1'). The gradient of is Lipschitz continuous on an open bounded convex set B that contains the level set, i.e., there exists such that

Definition 2.1. Let be the current iterate and B be an open bounded convex set that contains. We define a curve within B through as follows

where and is continuously differentiable on with and.

Definition 2.2. We call the one-dimensional function a forcing function if

where

It is obvious that the addition, the multiplication and the composite function of two forcing functions are also forcing functions.

In order to guarantee the global convergence of curve search methods, we suppose that the initial descent direction and the curve satisfies the following assumption.

(H2). The search curve sequence satisfies

where and are forcing functions.

Remark 1. In fact, if there exist and such that and

where then the curve sequence satisfies (H2).

This kind of curves are easy to find. For example,

are curves that satisfy (H2) and so are the following curves

(for), provided that and are bounded for all.

Remark 2. If is twice continuously differentiable and there exist M and such that

and for all, then the curve sequence satisfies (H2) be-

cause of

and

Remark 3. In line search methods, if we let and be bounded for all k, then satisfies (H2). As a result, line search method is a special one of curve search methods and its convergence can be derived from the convergence of curve search methods.

In the sequel, we describe the curve search method.

Algorithm (A).

Step 0. Choose and set.

Step 1. If then stop else go to Step 2;

Step 2. Let be defined by Definition 2.1 and satisfies (4). Set where is selected by some curve search rule;

Step 3. Set and go to Step 1.

Once the initial descent direction and the search curve are determined at the k-th iteration, we need to seek a step size such that

For convenience, let satisfy (4). There are several curve search rules as follows.

(a) Exact Curve Search Rule. Select an to satisfy

(7)

(b) Approximate Exact Curve Search Rule. Select to satisfy

(8)

(c) Armijo-type Curve Search Rule. Set, , and. Choose

to be the largest in such that

(9)

(d) Limited Exact Curve Search Rule. Set and. Choose to satisfy

(10)

(e) Goldstein-type Curve Search Rule. Set Choose to satisfy

(11)

(f) Strong Wolfe-type Curve Search Rule. Set and. Choose to satisfy simul- taneously

(12)

and

(13)

(g) Wolfe-type Curve Search Rule. Set and. Choose to satisfy simultaneously

(12) and

(14)

Lemma 2.1. Let be defined in Definition 2.1 and satisfies (4). Assumptions (H1) and (H2) hold and let. Then

where is a forcing function.

Proof. Assumption (H1) and Definition 2.1 imply that is uniformly continuous on B and thus, there exist and a forcing function such that

(15)

By (H2), Definition 2.1 and (15), noting that and, we have

□

Lemma 2.2. If (H1) holds and is defined by Definition 2.1 and satisfies (4), then is well defined in the seven curve search rules.

Proof. Let. Obviously,. The following limit

implies that there exists such that

Thus

which shows that the curve search rules (a), (b), (c) and (d) are well-defined.

In the following we prove that the curve search rules (e), (f) and (g) are also well-defined.

For the curve search rule (e), (H1) and

imply that the curve and the line must have an intersection point and thus

which shows that the curve search rule (e) is well-defined.

For the curve search rules (f) and (g), (H1) and

imply that the curve and the line must have an intersection point and suppose that is not the origin (0,0) but the nearest intersection point to (0,0). Thus

(16)

and

(17)

where. Using the mean value theorem, there exists such that

By (16) we have

and thus,

Therefore,

(18)

Obviously, it follows from (17) and (18) that satisfies (12) and (14) (also satisfies (12) and (13)). This shows that the curve search rules (f) and (g) are well-defined.

□

3. Global Convergence

Theorem 3.1. Assume that (H1), (H1') and (H2) hold, is defined by Definition 2.1 and satisfies (5) and

(19)

where is a constant. If is defined by the curve search rules (a), (b), (c) or (d) and Algorithm (A) generates an infinite sequence, then

Proof. Using reduction to absurdity, suppose that there exist an infinite subset and an such that

(20)

(H1) implies that has a bound, say, i.e., , and thus

Let

In the case of, for the curve search rule (c), there must exist such that

(21)

because of

By (9) and (21) we have

By (H1) we can obtain

which contradicts (20).

In the case of, there must exist an infinite subset such that

(22)

Therefore, for sufficiently large, implies that and

Using the mean value theorem on the left-hand side of the above inequality, there exists such that

and thus

Hence

(23)

By (22), (23) and Lemma 2.1, we have

which also contradicts (20).

In fact, we can prove that for the curve search rule (c). If then there exists an infinite subset such that (22) holds and thus, (23) holds. By (19), (5), (H1'), the mean value theorem, (H2) and (22), we have

This contradiction shows that.

For the curve search rules (a), (b) and (d), since for the curve search rule (c), let be the step size defined by the three curve search rules (a), (b) and (d), and let be the step size defined by the curve search rule (c), then we have

This and (H1) imply that

holds for the curve search rules (a), (b) and (d), which contradicts (20). The conclusion is proved.

□

Theorem 3.2. Assume that (H1) and (H2) hold, is defined by Definition 2.1 and satisfies (5) and (19), is defined by the curve search rules (e), (f) or (g). Algorithm (A) generates an infinite sequence. Then

Proof. Using reduction to absurdity, suppose that there exist an infinite subset and an such that (20) holds and let

For the curve search rules (e), (f) and (g), in the case of, by (11), (12) and (5), we have

By (H1) we have

which contradicts (20).

In the case of, there must exist an infinite subset such that (22) holds. For the curve search rule (e), by the left-hand side inequality of (11) and using the mean value theorem, there exists such that

Thus

(24)

By (22), (24) and Lemma 2.1, we have

which contradicts (20). For the curve search rules (f) and (g), by (14), (22) and Lemma 2.1, we have

which also contradicts (20).

The conclusions are proved.

□

Corollary 3.1. Assume that (H1), (H1') and (H2) hold, is defined by Definition 2.1 with satisfying (5) and (19), is defined by the curve search rules (a), (b), (c), (d), (e), (f) or (g), and Algorithm Model (A) generates an infinite sequence. Then

Proof. By Theorems 3.1 and 3.2, we can complete the proof.

□

4. Convergence Rate

In order to analyze the convergence rate, we further assume that

(H3). The sequence generated by curve search method converges to, is a symmetric

positive definite matrix and is twice continuously differentiable on, where

.

Lemma 4.1. Assume that (H3) holds. Then there exist and such that

(25)

(26)

(27)

and thus

(28)

By (28) and (27) we can obtain, from the Cauchy-Schwartz inequality , that

(29)

and

(30)

Its proof can be seen from the book ( [3] , Lemma 3.1.4).

Lemma 4.2. Assume that (H2) and (H3) hold and is defined by Definition 2.1 and satisfies (5) and (19). Algorithm (A) generates an infinite sequence. Then there exist and such that

(31)

Proof. We first prove that (31) holds for the curve search rules (c), (e), (f) and (g), and then we can prove (31) also holds for the curve search rules (a), (b) and (d).

By (9), (11), (12) and (5), we have

(32)

Since, there must exist a such that

(33)

By (4), Cauchy Schwartz inequality and (19), we have

(34)

Let

If then the conclusion is proved. If there must exist an infinite subset such that

Letting

for (23),

for (24) and

for (13), we have

(35)

By (35), (23), (24), (14), (34) and Lemma 2.1, we have

The contradiction shows that does not occur and thus. By letting, where

(36)

we can obtain the conclusion.

For the curve search rules (a), (b) and (d), let denote the exact step size and denote the step size generated by the curve search rule (c). By the previous proof, we have

All the conclusions are proved.

□

Theorem 4.1. Assume that (H2) and (H3) hold and is defined by Definition 2.1 and satisfies (5) and (19). Algorithm (A) generates an infinite sequence. Then converges to at least R-linearly.

Proof. By Lemmas 4.1 and 4.2 we obtain

By setting

we can prove that In fact, by the definition of in the proof of Lemma 4.2 and (36), we obtain

By setting

and knowing, we obtain from the above inequality that

By Lemma 4.1 and the above inequality we have

thus

i.e.,

Therefore,

which shows that converges to at least R-linearly.

□

5. Some Implementable Version

5.1. How to Find Curves

In order to find some curves satisfying Definition 2.1 and (H2), we first investigate the slope and curvature of a curve. Given a curve satisfying, if it is twice continuously differentiable, then the slope of the curve at is and the curvature is. We hope that the curve is a descent curve at, i.e.. Generally, we require to satisfy

where and. Moreover, we expect the curves to satisfy

It is worthy to point out that many convergence properties of curve search methods remain hold for line search method. In fact, the line satisfies Definition 2.1 and (H2), provided that is bounded for For example, we take with

(37)

where m is a positive integer and

We can prove that satisfies Definition 2.1 and (H2) under some mild conditions. Numerical results showed that the curve search method was more efficient than some line search methods [16] .

Another curve search method is from [15] with the curve defined by where

(38)

and

(39)

This curve also satisfies Definition 2.1 and (H2) with satisfying (5) under certain conditions and has good numerical performance.

Moreover, many researchers take

and satisfies (4) [20] . Certainly, we can obtain some curves by solving initial problems or boundary- value problems of ordinary differential equations and sometimes by using interpolation technique. Lucidi, Ferris and Roma proposed a curvilinear truncated Newton method which uses the curve

with being the quasi-Newton direction and being the steepest descent direction. This method also has good numerical performance [18] [19] because it reduces to quasi-Newton method finally and avoids some disadvantages of quasi-Newton method at the initial iterations. We guess that there may be many curve search methods which are superior to line search methods in numerical performance.

For example, if we take and suppose that and are uniformly bounded for k, then the following curve

satisfies (H2), provided that is bounded. In the following we shall test some curve search methods.

5.2. Numerical Experiments

In this subsection, some numerical reports are prisented for some implementable curve search methods. First of all, we consider some curve search methods with memory gradients. The first curve search method is based on the curve

(40)

The second curve search method is to use the curve

(41)

and the third curve search method searches along the curve at each iteration

(42)

We use respectively the Armijo curve search rule and the Wolfe curve search rule to the above three curves to find a step size at each step. Test problems 21 - 35 and their initial iterative points are from the literature [21] . For example, Problem 21 stands for the problem 21 in the literature and so on.

In the curve search rules (c) and (g) we set the parameters and. Numerical performance of the three curve search methods is reported in Table 1 and a pair of numbers means that the first number denotes the number of iterations and the second number denotes the number of functional evaluations. “P” stands for problems, n is the dimension of problems and T denotes total CPU time for solving all the 15 problems. We denote A1, A2 and A3 the curve search methods with the curves (40), (41) and (42) respectively. A1(c) and A1(g) means the A1 algorithm with the curve search rule (c) and the A1 algorithm with

Table 1. Iterations and function evaluations.

the curve search rule (g) respectively, and so on. The stop criteria is

It is shown in Table 1 that curve search methods with memory gradients converge to the optimal solutions stably and averagely. In addition, curve search methods with the Wolfe curve search rule are superior to the methods with the Armijo curve search rule. This shows that L = 1 seems to be an inadequate choice in the Armijo curve search rule and we can take L variably at each step similarly as in the literature [16] .

Moreover, many line search methods may fail to converge when solving some practical problems, especially when solving large scale problems, while curve search methods with memory gradients always converge stably. From this point of view, we guess that some curve search methods are available and promising for optimization problems.

6. Conclusions

Some curve search methods have good numerical performance and are superior to the line search methods to certain extent. This motivates us to investigate the general convergence properties of these promising methods.

In this paper we presented a class of curve search methods for unconstrained minimization problems and proved its global convergence and convergence rate under some mild conditions. Curve search method is a generalization of line search methods but it has wider choices than line search methods. Several curve search rules were proposed and some approaches to choose the curves were presented. The idea of curve search methods enables us to find some more efficient methods for minimization problems. Furthermore, numerical results showed that some curve search methods were stable, available and efficient in solving some large scale problems.

For the future research, we should investigate more techniques for choosing search curves that contain the information of objective functions and find more curve search rules for the curve search method.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Vrahatis, M.N., Androulakis, G.S., Lambrinos, J.N. and Magoulas, G.D. (2002) A Class of Gradient Unconstrained Minimization Algorithms with Adaptive Stepsize. Journal of Computational and Applied Mathematics, 114, 367-386. http://dx.doi.org/10.1016/S0377-0427(99)00276-9
[2]	Nocedal, J. and Wright, J.S. (1999) Numerical Optimization. Springer-Verlag New York, Inc., New York. http://dx.doi.org/10.1007/b98874
[3]	Yuan, Y.X. (1993) Numerical Methods for Nonlinear Programming. Shanghai Scientific & Technical Publishers, Shanghai.
[4]	McCormick, G.P. (1975) An Arc Method for Nonlinear Programming. SIAM Journal on Control, 13, 1194-1216. http://dx.doi.org/10.1137/0313075
[5]	Zang, I. (1978) A New Arc Algorithm for Unconstrained Optimization. Mathematical Programming, 15, 36-52. http://dx.doi.org/10.1007/BF01608998
[6]	Botsaris, C.A. (1978) Differential Gradient Methods. Journal of Mathematical Analysis and Applications, 63, 177-198. http://dx.doi.org/10.1016/0022-247X(78)90114-2
[7]	Botsaris, C.A. (1978) A Curvilinear Optimization Method Based upon Iterative Estimation of the Eigensystem of the Hessian Matrix. Journal of Mathematical Analysis and Applications, 63, 396-411. http://dx.doi.org/10.1016/0022-247X(78)90085-9
[8]	Botsaris, C.A. (1978) A Class of Methods for Unconstrained Minimization Based on Stable Numerical Integration Techniques. Journal of Mathematical Analysis and Applications, 63, 729-749. http://dx.doi.org/10.1016/0022-247X(78)90068-9
[9]	Botsaris, C.A. and Jacobson, D.H. (1976) A Newton-Type Curvilinear Search Method for Optimization. Journal of Mathematical Analysis and Applications, 54, 217-229. http://dx.doi.org/10.1016/0022-247X(76)90246-8
[10]	Flam, S.D. (1992) Solving Convex Programming by Means of Ordinary Differential Equations. Mathematics of Operations Research, 17, 290-302. http://dx.doi.org/10.1287/moor.17.2.290
[11]	Syman, J.A. (1982) A New and Dynamic Method for Unconstrained Minimization. Applied Mathematical Modelling, 6, 449-462. http://dx.doi.org/10.1016/S0307-904X(82)80007-3
[12]	Schropp, J. (1997) A Note on Minimization Problems and Multistep Methods. Numerische Mathematik, 78, 87-101. http://dx.doi.org/10.1007/s002110050305
[13]	van Wyk, D.J. (1984) Differential Optimization Techniques. Applied Mathematical Modelling, 8, 419-424. http://dx.doi.org/10.1016/0307-904X(84)90048-9
[14]	Wu, X.Y., Xia, J.L. and Ouyang, Z.X. (2002) Note on Global Convergence of ODE Methods for Unconstrained Optimization. Applied Mathematics and Computation, 125, 311-315. http://dx.doi.org/10.1016/S0096-3003(00)00133-8
[15]	Shi, Z.J. and Shen, J. (2005) A New Descent Algorithm with Curve Search Rule. Applied Mathematics and Computation, 161, 753-768. http://dx.doi.org/10.1016/j.amc.2003.12.058
[16]	Shi, Z.J. (2004) Convergence of Multi-Step Curve Search Method for Unconstrained Optimization. Journal of Numerical Mathematics, 12, 297-309. http://dx.doi.org/10.1515/1569395042571292
[17]	Amaya, J. (1985) On the Convergence of Curvilinear Search Algorithms in Unconstrained Optimization. Operations Research Letters, 4, 31-34. http://dx.doi.org/10.1016/0167-6377(85)90048-3
[18]	Ferris, M., Lucidi, S. and Roma, M. (1996) Nonmonotone Curvilinear Line Search Methods for Unconstrained Optimization. Computational Optimization and Applications, 6, 117-136. http://dx.doi.org/10.1007/BF00249642
[19]	Lucidi, S. and Roma, M. (1997) Numerical Experiences with New Truncated Newton Methods in Large Scale Unconstrained Optimization. Computational Optimization and Applications, 7, 71-87. http://dx.doi.org/10.1023/A:1008619812615
[20]	Ben-Tal, A., Melman, A. and Zowe, J. (1990) Curve Search Methods for Unconstrained Optimization. Optimization, 21, 669-695. http://dx.doi.org/10.1080/02331939008843594
[21]	Moré, J.J., Garbow, B.S. and Hillstrom, K.H. (1981) Testing Unconstrained Optimization Software. ACM Transactions on Mathematical Software, 7, 17-41. http://dx.doi.org/10.1145/355934.355936