Received 24 March 2016; accepted 24 April 2016; published 27 April 2016

1. Introduction
Understanding is based on models. Modelling is a way to describe a part of the universe―denoted the system under study―by creating a model, or theory, that is useful for a given purpose. The intention behind all types of models (mental, physical, analogous, mathematical or numerical) is to provide a very simplified description of important aspects of a system under study. The principle of parsimony, also denoted Occam’s razor, can be phrased as: “A scientific theory [model] should be as simple as possible, but no simpler.” (A. Einstein). This also means that “there are no true models―but some are useful” (G. Box).
In this paper, we confine our attention to the field of population models that are intended to be used for simulation. A population model is a type of model that is applied to the study of population dynamics. Central in such models are the concepts of births and deaths, which may include creation, immigration, emigration, destruction etc. For the mathematical theory of deterministic and stochastic population models, see e.g. [1] .
Here we use the word population in a wide meaning, including not only individual humans or animals, but also e.g. cars in traffic or production of items, perhaps in a queuing situation. For example, a model of a farm with a few workers, two tractors, a harvester and some trailers can be regarded as a population model. Population models are common in many fields such as demography, ecology, epidemiology, traffic studies and manufacturing, where queues are an important aspect, and also in physics and chemistry.
Using numerical methods, considerably more complex models can be constructed and studied than is possible with only mathematical and statistical methods. Moreover, when no analytical solution can be obtained, the numerical approach makes it possible to stepwise update (simulate) the model’s behaviour over time and space.
A general methodology for model building and simulation has been developed, accepted and used for more than half a century. It prescribes that the model study be organised as a project containing a well-defined sequence of consecutive phases. Apart from terminology, which varies somewhat, a model study should contain the following sequence of project phases: problem definition, model building, validation of model, analysis based on the validated model, result evaluation and result presentation [2] - [6] . It is also stressed that this process is highly iterative, because learning occurs during the process and makes it necessary to go back and refine the model.
The content and methods of each phase are well defined, except for the model building phase. For population studies, there are a number of quite different modelling approaches―based on different ideas and concepts― that can be used. The main classical approaches are outlined in Section 1.2. These approaches have their pros and cons for different purposes and population systems under study. They may produce different results and conclusions unless some crucial rules, which are presented in this paper, are strictly followed. This lack of scientifically based general rules for the model building phase has often led to unmotivated approaches or ad hoc constructions of the model. Therefore, modelling and simulation are often regarded as a mixture of art and science.
1.1. The Aim of This Paper
The aim of this paper is to complement the science on the model building phase for population models by clarifying the fundamental constituents of a numerical model of populations under study, and to show how a unified theory of population models can be based on these constituents. It is also our explicit aim to present the paper as a tutorial.
To avoid confusion, it was necessary to find unambiguous terms that work for all types of population models. For example, the term “state”, which has different meanings for different types of model, usually has to be avoided. It was also necessary to introduce and rename some terms.
Furthermore, it was necessary to clearly separate the concepts of the system under study from those of the model world. We observe the objects in the system under study and describe them as subjects that can act in a simulation model. Therefore, the following convention is used throughout: The system under study, containing a population of objects, is described by a set of subjects in the model.
Depending on the purpose, the modeller is free to model each object as a separate subject, to aggregate subjects into different compartments or even to describe the population as a continuous substance, provided that this does not introduce misleading results.
Within this scope of this paper we discuss a number of central issues, such as:
How can a conceptual model be constructed, from the purpose(s) and the system under study?
How can an executable simulation model be made from the conceptual model?
When and how can different types of models be translated into another type?
When will a discrete model and a continuous model give consistent results?
What factors of the population system under study and the problem definition should cause the modeller to choose or avoid specific types of models?
How does the type of model affect the study in terms of required information, size of the model and possibility to include different types of stochasticity?
Note that this paper is not about how to perform a complete modelling study over the sequence of project phases and the iterations involved, nor is it about specific simulation languages or various techniques such as parameter estimation, integration methods, validation or statistical post-processing over many replications. The focus is instead on the “anatomy” of the model, i.e. the main constituent elements and their interrelations, the options available and the consequences of selecting one rather than another of these options.
1.2. Modelling Paradigms and Tools
In this section we briefly introduce some of the classical types of models that exist, roughly in the order in which they were first proposed.
While mental modelling and mental simulation certainly go back to prehistoric times, scientific modelling based on e.g. physical properties of the system under study and expressed in mathematical terms has developed gradually in an ad hoc manner, to handle different issues, during the past few centuries.
A significant milestone is dynamic modelling, which goes back to Isaac Newton [7] . A system of ordinary differential equations is then solved over time, so that the dynamics generated by a physical structure can be revealed in the form of e.g. trajectories over time. In this paper we classify this as deterministic compartment- based modelling. A Continuous System Simulation Language may be used for simulating such models.
With the introduction of Monte Carlo methods/simulation in the Manhattan project, the stochastic part of simulation started to develop significantly. The idea behind Monte Carlo simulation is to perform repeated random experiments to obtain numerical estimates of an unknown quantity. This idea was first proposed by Georges Louis Leclerc, Comte de Buffon, in the paper Sur le jeu de franc-carreau, published in 1777. Monte Carlo methods are mainly used for optimisation, numerical integration and generating draws from a probability distribution. The development of random number generators for different distributions is an important heritage included in most types of simulation packages.
In 1906, Markov chain models were developed as a mathematical/statistical theory of stochastic processes [8] [9] . Later, the development of digital computers made this approach more practically useful. We classify this as situation-based modelling in our vocabulary.
With digital computers, numerical methods and various kinds of simulation languages, the number of modelling and simulation approaches virtually exploded during the second half of the 20th century.
In 1961, the entity-based simulation language GPSS was constructed by Geoffrey Gordon [10] . In GPSS, the objects are represented by entities (sometimes called transactions) with identity and attributes (called parameters) that move in a flowchart, which connects various types of stations (called blocks). For these languages, a large number of random number generators for different statistical distributions are included. A drawback with entity-based simulation models is that the number of modelling primitives (station blocks and transport facilities) becomes very large, but still without covering all possibilities.
With SIMULA (1967), the concept of classes of subjects (called “objects”) containing both attributes and procedures was introduced [11] . This opened the way for agent-based simulation. Originally, simulation in SIMULA was performed by the built-in “Class Simulation”. Later on, the powerful “Class DEMOS” [12] could be used for efficient agent-based modelling. The number of concepts and constructions could then be reduced to a small number, leaving details to be specified in the host language SIMULA―an “object-oriented” general- purpose programming language.
Stochastic compartment-based modelling was first presented in 1976 by Daniel Gillespie. He used event scheduling in a two-step manner in his Stochastic Simulation Algorithm (SSA). In 2000, Gustafsson [13] described how Poisson-distributed random numbers could be systematically used for stochastic compartment- based models to efficiently and accurately handle transition stochasticity. Three years later, an extension showed that queues could also be implemented in compartment-based models in a straightforward way [14] . This led to a convenient way to use compartment-based models to investigate stochastic population models.
1.3. Some Previous Work on Unifying Frameworks
There have been a number of attempts to systemise simulation models, to investigate consistency for models in different representations or to compare the merits of different types of simulation models.
In the book “System Simulation: Programming Styles and Languages” [4] , simulation is classified by Kreutzer into four paradigms: “Monte-Carlo methods, continuous, discrete event and combined simulation all have their own methodologies, tools, traditions, user communities and prototypical applications.” The four paradigms are not compared, but presented and discussed side by side.
In addition, a large number of papers compare or discuss (stochastic) individual-based models versus analytical models (differential or difference equation models) in a deterministic or stochastic setting, primarily within ecology; see e.g. [16] - [21] . In some of these papers the analytical model is regarded as the base for theory building and becomes a norm (instead of using the system under study as the norm, which we do in this paper). Discrepancies are often found because the assumed analytical model is deterministic or includes stochasticity simply as additive noise. However, we now know the correct ways of introducing different types of stochasticities into analytical models, which are presented and used in this paper. We have also recently clarified conditions for deterministic and stochastic analytical models to be consistent [22] .
In this paper we take a pragmatic approach, focusing on the “anatomical” aspect of what constituents are necessary to model a population system under study. Based on earlier studies [13] [14] [22] - [24] , the issues of con- sistency, how to translate between different model representations and pros and cons of choosing a specific representation are covered. The main issue is how well a population system under study can be conceptualised into a general conceptual model, and then realised in various ways.
1.4. Outline of the Main Concepts
A common mistake by modellers and readers of simulation-based studies is confusing real system and model. When performing population modelling to be used for simulation, we deal with a system under study, a conceptual model description of this system and a realisation in the form of an executable numerical model, in the following denoted a simulation model. To distinguish between these contexts as clearly as possible, we introduce the picture of different “worlds” in which the system under study, the conceptual model and possible alternative simulation models of it reside.
q The SYSTEMS WORLD contains the system under study as an actual, historical, future, assumed or possible reality.
q The CONCEPTUAL WORLD is an intermediate world where the purpose of the study and the main components of the system under study are specified in terms of a conceptual model. Here the focus is on what to model.
q The SIMULATION MODELS WORLD is where a simulation model is created from the conceptual model, in order to behave in (almost) the same way as the system under study from the point of view defined by the purpose of the study. The simulation model can then be used for calculations and experiments. Here the focus is on how to model it.
Modelling a system under study for a given purpose is a stepwise procedure, moving from selected properties of the systems world via the conceptual world to the simulation models world where we construct a simulation model. An “anatomical” sketch of the main elements and how they are translated between the different worlds is provided in Figure 1. The figure also gives an outline of the organisation and content of this paper.
Our aim is to clearly distinguish between the three worlds. In the systems world we have objects with properties and behaviours. In the conceptual world and the simulation models world we think of this in terms of subjects with attributes and procedures. Here we can choose between the discrete, continuous or combined model category―a choice that will have a profound influence on the simulation model and its behaviour.
![]()
Figure 1. An “anatomical” sketch of the construction elements in modelling a population system. Left: The systems world. Centre) The conceptual world. Right: The simulation models world. Note that the purpose and the system under study are both required when specifying the conceptual model. These and other characteristics also affect the realisation of a simulation model. This figure defines six main constituents of a simulation model that have to be conceptualised and realised. Details of the figure are explained in the following chapters.
2. The Systems World
The universe as we know it is immensely huge and complex, with some 1080 atoms forming various hierarchies of interacting parts. In different sciences and other contexts, different parts of the universe are studied at different aggregation levels and with different purposes. The system to be studied may be an actual part of reality, but it may also be an historical or a future situation or an assumed or possible reality.
Our knowledge of a system comes from previous observations, measurements, experiments and conclusions. It contains information about the elements, how these elements form a structure and the relations between the elements. We may also be interested in the behaviour of the system. However, this knowledge can be on different levels of aggregation. It may concern elementary particles, atoms, molecules… up to organs, individuals, buildings, cities, planets, solar systems, galaxies etc.
Furthermore, the boundaries between the system under study and its environment are generally not closed. Even with carefully defined system boundaries, there is usually some form of interchange of material, energy or information between the system and its environment that may also have to be considered. There may be inflows and outflows of objects through the system boundaries, and the environment may influence the system’s behaviour.
Since population modelling is of interest here, the system under study will contain a population of discrete objects. These objects can also have a number of properties and behaviours. For example, objects can have the properties age, sex, position etc. and behaviour that can be to approach, avoid or react to a certain situation.
All the above-mentioned aspects are necessary to consider in the subsequent modelling of a particular system, where the system under study can be regarded as a database of more and less relevant information. This is treated in the following chapters.
3. The Conceptual Model (What to Model)
3.1. Introduction
A model study usually starts after some kind of problem recognition―something is interesting, behaves in a strange way, does not work well, could perhaps function in a different way etc. Therefore, the modeller wants to understand why or how, reduce costs or improve performance.
A conceptual model is then required to provide concepts for thinking and communication and, later on, to act as a blueprint for creating a simulation model.
We focus here on the first two phases of a modelling project introduced in Chapter 1, namely problem definition and model building. The problem definition phase should lead to a conceptual model―a blueprint of what the model should describe. The following modelling phase then takes the conceptual model into an executable form by determining how the model should be technically realised.
The problem definition has two main parts:
Formulation of the purpose of the study.
Definition of the system under study and important influences from its environment.
The purpose of a study should be carefully defined in operative terms. It may concern understanding, performance, control or optimisation. Formulating the purpose is an entirely subjective part of a study, but the aim should then be to perform the rest of the study using proper scientific methods.
Only after formulation of a concrete purpose is it possible to specify a proper system under study. The specification process helps comprehend the system under study based on knowledge and observations from the perspective of the purpose.
The definition of the system under study includes:
-Defining the system, its boundaries, inflows and outflows, and influences from the environment.
-Choice of an aggregation level appropriate to the purpose. This also refers to the resolution in space and time.
-Specifying the time period of interest.
The modeller is usually interested in describing one level of aggregation or a few levels forming an hierarchical structure.
Based on the purpose and specifications of the system under study, it is time to create a conceptual model of the population system that contains the main components and sketches their interrelations.
3.2. The Constituents of a Conceptual Model of a Population System
When constructing a conceptual model, we have to consider what components should be described as discrete or as continuous, how to handle lack of information about structure or behaviours, how to formulate the purpose in terms of the model’s components or behaviour and how space and time should be represented. We also have to specify the time period to be studied.
The decisions made about these constituent issues have a profound effect on the construction of the simulation model and its results, as discussed in Chapters 4, 5 and 6. Here we briefly discuss the fundamental concepts necessary to formulate the conceptual model. These six main issues, listed as points (1) to (6) in the “Conceptual World” part of Figure 1, are:
(1) Model category
An overriding decision is whether to conceptually think of the system under study as composed of (A) discrete elements, (B) continuous “matter” or (C) a mixture of these. This decision leads to different model categories that have far-reaching consequences for how the final model can be represented and for what types of questions can be answered. Except in special cases, different model categories may create different behaviours and results.
(1A) In the discrete model category, objects are described as discrete subjects.
(1B) In the continuous model category, the population of objects is described as a continuous, infinitely divisible substance with a set of attributes (e.g. position, velocity, temperature, age or health state). Here fractions of the substance can have different attribute values. For example, water is represented as a continuous substance instead of molecular subjects.
Large simplifications can sometimes be achieved by using a continuous model. It is the nature of the system and the purpose that decides whether such a simplification can be made without jeopardising the results. In Chapter 5 we show that many options for discrete modelling disappear or become incompatible with the continuous case as a direct or indirect consequence of the assumption of unlimited divisibility of the studied substance. Only under particular conditions (discussed in Section 5.3) will the continuous model category produce consistent results for a population study.
There are two main reasons for choosing a continuous approach, although a population system under study is ultimately composed of discrete objects:
-The number of objects may be so large that it is practical, and consistent with the purpose, to regard them as a continuous substance.
-A simpler deterministic and continuous model can for practical reasons be used when it produces consistent estimates. This can be of great value for optimisation, parameter estimation and sensitivity analysis.
(1C) The combined model category contains elements from both the discrete and the continuous model categories. However, the discrete and continuous sub-models must be synchronised in time―preferably, but not necessarily, using the same time handling method.
(2) Conceptual representation
A conceptual representation is a skeleton that directly or indirectly describes the objects with their properties and behaviours either as discrete subjects using the discrete model category, or as a continuous substance using the continuous model category. In both these model categories, the properties and behaviours of the objects have to be described by attributes and procedures. In the discrete model category the attributes can be related to the subjects individually or collectively. For individually described subjects their identities can, if required, be preserved in the model. In the continuous model category the attributes are related to fractions of a continuous substance, and there is no identity of an individual subject.
An attribute can be constant (e.g. sex, date of birth) or it can change over time (e.g. age, weight, health status). The attributes can also affect what happens in a procedure or can be changed by the procedure. For a spatial population model, the position in e.g. three dimensions can be represented by x, y and z attributes.
A procedure generates actions or changes that affect the subject, other subjects or other parts of the model (or fraction of a substance in a continuous model description). In both the discrete and the continuous cases the procedures can be described by a flowchart of stages and possible transitions (flows) between stages, where the subjects or fractions of substance are transferred. A stage represents a combination of attribute values, for example: Female & Infectious. Each stage then represents the attribute values of the subjects or fraction of substance located in it.
The transition to another of several possible stages can depend on the outcome of a conditional statement, which in turn may depend on attribute values or other quantities in a deterministic or stochastic way.
A subject (in a discrete model) or fraction of substance (in a continuous model) may reside in a stage for a sojourn time, which may be deterministic or random according to a statistical “sojourn time distribution”. However, the duration in a stage can also depend on conditions external to the stage. See the example in Figure 2.
In the Clinical stage in Figure 2, a subject has a probability to be successfully treated or to die during a short time interval. (In a continuous model a fraction of substance will replace the probability of departing from the stage.) However, the departures from the Healthy stage and the arrivals to the Dead stage in Figure 2 are regulated by conditions outside these stages, so the Healthy and Dead stages have no defined sojourn time distributions.
![]()
Figure 2. A simple procedure of a disease process expressed as the stages: Healthy, Preclinical stage, Clinical stage and Dead, and possible transitions between stages. (We denote a stage by a double-framed rectangle.)
In both the discrete and continuous cases, a stage can have one or several different sojourn time distributions, which define the sojourns (residence times) in the stage for one or more possible paths between entrance and exit points. The sojourn time can be constant, dependent on conditions outside the stage, or represented by a sojourn time probability distribution.
The purpose, the available information and other factors may also affect the process description. For example, if the purpose is to find the subject with the shortest transition time through a system, then this requires each subject to be identifiable so it can be followed over time. In the continuous model category there are no individual subjects, so a continuous model would be unsuitable in this case.
In Chapter 4, four ways to realise a conceptual representation as a discrete simulation model are introduced.
(3) Uncertainties about structure and behaviours
The model must use existing or available knowledge and information that is never complete and perfect. Therefore, incomplete knowledge about the system under study will remain. Five types of uncertainty can be distinguished:
Incomplete knowledge about the structure of the system under study (Structural uncertainty).
Irregularities in the occurrences of transitions between stages. Even when we know that a subject is in a certain stage, we may not know exactly for how long it will remain there or which stage it will go to next (Transition uncertainty).
Inexact information about initial conditions at the defined initial time (time zero) (Initial value uncertainty).
Unexplained influences from the environment of the system may also have to be considered and modelled as possible sets of parameter values (Parameter uncertainty).
Irregularities in the information transferred. This may be information between objects or information about objects or situations etc. We denote such information signals. A signal can affect other parts of the system (e.g. a stop signal, an order or warning, a signal as part of a control system). However, the signals may be delayed or distorted for a number of reasons. The messenger may be delayed, the broadcasting may be disturbed by noise or misinterpreted, the whole or part of the message may be lost etc. Therefore, we may not know exactly for how long a message will be delayed and if and how it is distorted (Signal uncertainty).
The structural uncertainty can only be handled by alternative models. The difference in behaviour for these alternative models can then give an approximate indication of the uncertainty in the results because of structural uncertainty.
The other four types of uncertainty can be statistically described by probability distribution/density functions (pdfs). These pdfs can then be included as parts of the conceptual model. Later on, when constructing a simulation model, random number generators can draw random numbers from the appropriate statistical distributions during the simulation. This results in a stochastic simulation model. (A model without any stochasticity is a deterministic model.)
To correctly estimate the uncertainty in model results and estimates, for example in the form of confidence intervals, it is crucial to include the effects from all five types of uncertainty.
(4) Output of interest
The purpose must usually be included in the conceptual model and formulated in terms of the model concepts chosen. If, for example, we want to minimise the harm to a particular forest, this harm has to be formulated in terms of the trees, animals, soil etc. So the purpose is an important part of the model, even though the purpose is subjectively defined and therefore does not exist within a system under study.
(5) Time concept
Time is conceived as a continuously progressing scalar quantity, but in a model, time can be considered as a continuously increasing quantity (as in a differential equation), a quasi-continuous time (as in a difference equation), or as a sequence of event times when something important happens. The choice of time concept can be postponed until construction of the simulation model.
(6) Time period of interest
A simulation model can be used to study the system over various time periods. What needs to be contemplated while developing the conceptual model is the type of time period that is of interest. Is there a predefined start time or do we want to describe each object from the time of some type of individual exposure or event? Will the end point of the simulation study be a pre-specified point in time (definite termination criterion) or when a certain condition is satisfied, e.g. an epidemic is over (indefinite termination criterion)? In the latter case, the termination time will depend on what happens in the model during each simulation run. These issues are discussed further in Section 4.6.
Both a conceptual model and a simulation model include a number of components that go beyond the boundaries of the system under study.
First, the model has to include a description of important interactions over the system boundaries. For a population model this can be physical inflows and outflows of objects because of births/deaths, immigration/ emigration, import/export or vehicles passing in and out of a city. Furthermore, the environment may influence the system behaviour in different ways. The system boundaries correspond more to a structural (core) part of the model describing how the key components interact to generate the process of interest, while the influences from outside the system boundaries are modelled as constant, time varying or irregularly varying quantities that are themselves unexplained within the model.
Second, the model contains a number of man-made concepts and components that may have no counterpart in the system under study―for example concepts such as stage, compartment and situation, the purpose formulated as a output (function), statistical distributions to make use of incomplete information and artificial time handling.
4. The Discrete Simulation Model
The conceptual model defines what to study and consider, but not how to realise it as a simulation model. To construct a simulation model, we must specify which options to use from each of the six constituents presented in the right-hand part of Figure 1.
Point 1, the model category (Discrete, Continuous or Combined) used to reproduce the nature of the system under study, is crucial for the construction of a simulation model. It has such far-reaching consequences that it is necessary to subordinate the other points (2. Model representation, 3. Uncertainties, 4. Output functions, 5. Time handling and 6. Start & Termination criteria) under each model category. Some of the alternatives for constituents (2) to (6) may result in loss of information or distort the model’s behaviour.
4.1. The Discrete Model Category
For pedagogical reasons, we start with the discrete model category. A discrete model with an integer number of separate subjects is used here to describe the objects of a population under study. The discrete model category (1A) contains a “complete framework”, where all the listed options of constituents (2) to (6) are valid choices. Based on this framework, in Chapter 5 the continuous model category is then briefly explained as a simplification of the discrete model category.
Objects in a population under study may also interact with internal or external continuous processes that need to be included in a model. In such a case, we can sometimes stay within the discrete model if we can describe the development with, for example, time functions―but if we have to model dynamic interaction between the discrete and the continuous developments, we may have to use the combined approach presented in Chapter 6. In Chapter 4, we only focus on models with discrete subjects.
4.2. Model Representation
As described in Chapter 3 for the conceptual representation, an object in the system under study can be represented by a simplified subject having optional attributes and procedures.
4.2.1. Attributes
A property of an object can be e.g. age, weight, position, fortune, speed, state of health or location. Properties may be constant in time (date of birth) or change with time (age). In a model, a property is represented by an attribute. This attribute serves as a memory that may change in accordance with what happens to the subject. An attribute may also affect the procedure of the subject. Thus, the attributes and procedures can interact.
An important distinction is whether the attribute takes discrete or continuous values. Discrete values such as sex or number of children can be represented by integers, while continuous attribute values such as position are represented by real values unless the attribute value is discretised into a number of intervals (thereby losing some information).
1) Attribute discretisation
In compartment-based and situation-based representations, a subject is sorted into one of a finite number of “boxes” (e.g. compartments or situations) based on the values of attribute sets. Whenever continuous attributes are discussed with the purpose of defining discrete sets of compartments or situations, discretisation of these attributes is necessary.
Sometimes, the discretisation may be so coarse that it hides or blurs the results that are important. This is called attribute discretisation error. However, the discretisation error can be reduced to a level considered negligible for the modelling purpose by using a finer subdivision of attribute values at the cost of modelling effort and execution time.
When a continuous property is represented by a finite number of attribute values or stages, functions of a discretised attribute will produce discretised outcomes. This also means that an event that takes place when a continuously varying property reaches a prescribed level will, in the model, be synchronised to happen when the corresponding attribute stepwise changes its value. So when an attribute is discretised, this can also affect a procedure.
In the following, we assume that appropriate discretisation has been performed for attributes that are used in the definition of discrete attributes or stages.
2) Spatial modelling
Spatial modelling can be implemented in a number of different ways―but they are all based on position attributes. A position attribute can be local to the subject and describe its location using the coordinates in some coordinate system. The space itself can also be globally represented by a fixed grid of position attributes in one, two or three dimensions, where each position attribute can take values such as {Occupied (by a subject), Empty} or {Normal cell, Tumour cell, None}.
Local position attributes. The position of an object can be described by a position attribute for each dimension of the space (e.g. using x, y and z coordinates). Spatial modelling is a huge and complex field, see e.g. [25] [26] . Whether the spatial qualities of a system under study are required in the model depends both on the system under study and on the purpose of the study. For many population models in demography, ecology, epidemiology, traffic planning etc., the positions of the subjects (persons, animals, plants, cars) are important for the behaviour of the model. For example, an infectious disease may spread only between people on the same spot. Modelling of migration, spread and control of diseases such as malaria, Ebola or AIDS, or behaviour of the vehicles in a traffic situation, requires information on the positions and movements of individuals to produce realistic behaviours and results. For an infectious disease that is spread by intimate contact, the networks of relations between objects may be more important than the spatial locations1.
In agent-based and entity-based models, the current position of a subject can be stored in position attributes for the coordinates x, y and z. The subjects are allowed to move continuously over the whole region in accordance with rules or statistical distributions. Brownian motion is one example. Methods to describe motions in continuous space are sometimes called “diffusion methods” [25] .
Global position attributes. In a compartment-based model, the spatial attributes have to be approximated (discretised) by a grid of compartments in one or more dimensions. The migration of subjects is then often only allowed to the immediate neighbouring sites. This is called a “stepping-stone” method [25] . A simple example of this is a random walk on a regular grid.
When the spatial aspect is central, an alternative is to use a cellular automaton, i.e. a model for studying cellular structures that was originally invented by Stanisław Ulam and John von Neumann in the 1940s. A cellular automaton consists of a grid of cells (i.e. a fixed global grid of position attributes) in one or more dimensions, where each cell can be in one of a finite number of “states”. For each cell, a set of neighbouring cells is defined. The cells of the grid are then simultaneously updated over time (generations) according to some deterministic or stochastic rule, which considers the current state of the cell and of the cells in its neighbourhood [29] . A stochastic cellular automaton is also denoted a locally interacting Markov chain [32] .
A cellular automaton can be constructed by letting the subjects of the population consist of cells, where each cell (except for its fixed attribute “position”) has an attribute that can take discrete values (“states”) such as {0, 1, 2, ...}, {Alive, Dead}, or {Normal cell, Tumour cell, None}.
The cellular automaton is in several regards more primitive than the types of models we treat in this paper. It is therefore appropriate for a much more restricted set of population modelling problems, but is sometimes convenient to use. Examples are: Self-organisation and spatial tumour development [30] [31] .
4.2.2. Procedures
Attributes define the state of the subject, while procedures2 specify how the subject will act under different conditions. A procedure can affect the attributes of the subject, the attributes of other subjects or global attributes. The procedure can be realised as programme code, as a flowchart or in matrix form. Irrespective of the form, the Structured Program Theorem applies [33] . This theorem states that it is possible to write any computer programme by using only three basic control structures: sequence, selection and repetition.
A procedure can be conceived as a logical track system of switches and stages (stations). The switches are realised by e.g. logical statements that, depending on some condition, determine the future of the subject, of other subjects or of global quantities. Subjects spend their time in stages. A transition between stages is modelled as instant, because a subject cannot be in two stages at the same time. If a transition (e.g. a trip from A to B) takes time, then this transition is modelled as a stage holding the subject for the transition time. The time spent in a stage is denoted sojourn time (as described in point (2) in Section 3.2). This is a crucial quantity that can be constant, but is often drawn from a specified statistical distribution. The time spent in a stage can also be generated by waiting for external resources or by waiting for a condition to be satisfied.
A subject can interact with its surroundings3, e.g. with other subjects, or it may change the situation of the model in some way. One example is when a subject waits for a resource in competition with other subjects. Such waiting is modelled as a queue [12] [34] . The resource may be a permanent resource that is occupied for some time and then released (e.g. a taxi cab, elevator etc.) or a consumable resource (e.g. food, fuel etc.) that has to be produced before it is consumed. Priority may also be involved in the queuing.
4.2.3. Representation―Organising the Interaction between Procedures and Attributes
A subject (describing an object with its properties and behaviours) can be represented in different ways in a simulation model, depending on whether the attributes and procedures are modelled as part of the subject or external to it:
A subject can be an agent with both attributes and procedures.
A subject can be an entity with only attributes. The entities use a common external procedure.
A subject can be a token without any attributes or procedures. The token only has a location in the procedure, flowchart or track system. The token can have an identity (reference to it) so that it can be followed over time or it can be anonymous.
A subject can be part of the number of tokens in a compartment. The network of compartments then represents the procedure.
A subject can contribute to the total situation that the entire model can be in. The set of all possible situations are then arranged in a vector. The procedure is implemented as a transition matrix, where the elements are transition probabilities between situations.
Thus, the choice of representation is mainly about how and where to locate the attributes and procedures of the subjects. There are four possible representations, which we denote: Agent-based, Entity-based, Compartment-based and Situation-based. Because the representation has such a profound impact on the model, we also classify the models according to their representation as Agent-based, Entity-based, Compartment-based, and Situation-based models, abbreviated ABM, EBM, CBM and SBM, respectively4. Figure 3 shows these four types of model representations.
Agent-based representation (ABM)
The agent-based representation is the most straightforward. Here an object with its properties and behaviours of interest is represented by a one-to-one mapping to a subject with attributes and procedure(s). The agents may interact with other agents and with their surroundings, and may also be affected by their surroundings [12] .
Entity-based representation (EBM)
In an entity-based representation, the subject is an entity with attributes but no internal procedure. In this representation, entities with the same or similar behaviours can share an external procedure or logical track system of connected stations (stages) where the entities can move around. The sojourn time in a stage can have any distribution of non-negative values. In both ABM and EBM, each subject can be monitored and referred to [34] .
Compartment-based representation (CBM)
In a compartment-based representation, the subject is an anonymous token without any internal attributes and procedure. Here too, the subject’s procedure is an external track system of interconnected stages (not yet compartments) where the tokens can reside. The subject’s set of possible attribute values is defined by the present stage in which it is residing. In a compartment-based model, a stage contains the number of subjects residing in it, so the individual token is anonymous and cannot be individually followed over time.
For example, if the subjects” attributes are sex, age group and health status that can take the values {Male, Female}, {Child, Adult, Old} and {Healthy, Sick}, then 2 ´ 3 ´ 2 = 12 stages are required to represent all sets (combinations) of attribute values. If the study object is a woman, 27 years of age and sick, her corresponding subject in the model will be located in the stage “Female & Adult & Sick”. Thus the number of stages increases multiplicatively with the number of (discretised) attributes studied. This is called attribute expansion; see [24] .
For a compartment-based representation there is also another a complication: a stage is in general NOT a compartment, because a stage has a specific sojourn time distribution (e.g. Weibull, Erlang or an empirical distribution) and a compartment by nature has an exponential time distribution. Technically, it is necessary to use the exponential sojourn time distribution for a compartment, because this is the only memoryless continuous time distribution [5] . It is the memorylessness that allows superposition, whereby newcomers can mix with those already residing in the compartment without distorting the remaining time to departure. The solution to this
![]()
Figure 3. Discrete models of a population system under study based on different representations.
dilemma is to represent the stage by a structure of compartments in series and/or parallel to approximate the intended sojourn time distribution of the stage. This is denoted stage to compartment expansion (or distribution expansion), see [24] .
To simulate a compartment-based model, the model must be translated into difference equations (where the state variables are the compartments) to calculate the development over time [35] .
Situation-based representation (SBM)
In a situation-based representation, each situation that the entire system can take (as defined by the conceptual model) must be described5. Markov chain models [36] and chain-binomial models [37] belong to this type of representation. A situation-based model is closely related to the compartment-based model. Here too, the subjects are anonymous and only implicitly represented as part of a number. Again, it is crucial here to consider the sojourn time distributions of the stages―although these are often erroneously neglected. However, in contrast to a CBM, where the number of compartments is independent of the size of the population under study, the complexity and the size of an SBM grows combinationally with the population size.
In a situation-based model, the possible numbers of subjects in all compartments have to be combined to describe all situations the model can be in. For example, in a model with two interconnected compartments (A and B) and one subject, there are two situations to consider: the subject being in A or in B. With two subjects there are three situations: {A = 0 & B = 2, A = 1 & B = 1, A = 2 & B = 0}, but with n subjects to be distributed into k compartments there are n + k − 1 over k − 1 situations (“states” in Markov model terminology). Thus, the number of situations grows combinationally with both the number of compartments (in a corresponding compartment-based model) and with the number of subjects. Therefore, even a rather small compartment-based model may require a huge number of situations to be represented in a corresponding situation-based model. We call this expansion in model size combinational expansion, see [24] .
There are two methods of solving/executing an SBM: The first method is to mathematically take the Cartesian product of the situation (“state”) row-vector s(t) at time t and a transition matrix T to calculate the new situation vector s(t + 1). The elements in the situation vector then represent the probabilities of being at every possible situation. The transition elements Tij are the conditional probabilities of moving to situation sj(t + 1) when in si(t). In this way, all information is obtained in one sequence of calculations; t = 0, 1, 2, ... However, the situation vector and the transition matrix become huge even for rather small models if the population is not very small.
The second way is to use simulation to follow the development from situation to situation over time, by using random numbers to decide the next situation. The situation vector s(t) is then binary, with a single “1” at location i, representing the actual situation and all other elements being equal to zero. The situation row vector thereby selects the ith row of the transition matrix, T. A random number, drawn from the pdf represented by the ith row of T, decides which transition will be realised to create a new binary situation vector s(t + 1). In this way a “trajectory of situations” s(0), s(1), s(2), ... is created for each replication. This method requires a large number of replications, but is usually considerably faster than updating the whole pdf for a medium-sized SBM. Of course, some thousands of replications will not cover the whole “situation space”―but that is seldom required for achieving the purpose of the study. Situations are usually aggregated into more relevant measures, e.g. the purpose may be to study the number of infectious subjects in a SIR model where post-analysis aggregation is made over e.g. sexes and ages.
Hybrid representations
Other model approaches that are hybrids of those presented above can be used for simulation, for example Petri nets [38] . See Appendix C.
4.2.4. Relations between Model Representations
Example 1: Relations between model representations
A conceptual SIR model is an epidemic model composed of three stages: S (Susceptible), I (Infectious) and R (Recovered). In the particular population model considered here, each of 11 subjects meets everybody else. A Susceptible subject becomes infected by an Infectious subject with a specified probability per time unit and an Infectious subject recovers according to an assumed sojourn time distribution. This type of model was first formulated by W.O. Kermack and A.G. McKendrick [39] . To the stage attribute = {S, I, R} here we add the attribute sex = {Male, Female}. Furthermore, we specify the sojourn time of the Infectious stage as having the same 3-Erlang distributions for both males and females. Thus the infectious stage must be represented by three serially connected compartments in CBM [40] . In Figure 4 this conceptual model is represented as ABM, EBM, CBM and SBM.
Figure 4 demonstrates a sequence of transitions (T1 to T6) from one representation to another. It shows how an ABM of an infectious population can be stepwise translated via EBM and CBM into an SBM. The figure can be interpreted in the following way:
The ABM is just a 1:1 mapping of the Conceptual model described above. Each subject is represented as an agent with its attributes (Health status: {S, I, R} and Sex: {Male, Female}) and procedure (S ® I ® R), where the sojourn time distribution in the Infectious stage is considered. The S and R stages have no such defined sojourn time distributions.
T1 (inside out): The ABM can be transformed by T1 so that each agent is turned inside out in the sense that instead of having n agents with internal procedures (S ® I ® R), the procedures, in the form of n track systems, become external. Now these n procedures contain one subject each, placed in their current stages; S, I or R. The sex attribute, which remains unchanged, is still located within each subject.
T2 (Superposition): Next, the n track systems, one for each subject, are super-positioned into a common track system where each of the n subjects is located at its stage. We thereby obtain an EBM with entities whose sex attribute preserves their values of male or female.
T3 (Attribute expansion): The EBM can then be transformed so that it is expanded according to the attribute values {Male, Female}. Attribute expansion can be “costly” when there are several attributes that can take many values (or intervals of values if the attributes take continuous values). For example, with the attributes K, L and M taking k, l and m different values, respectively, the size of the model structure is multiplied by a factor of
![]()
Figure 4. The conceptual SIR model in Example 1, with n = 11 subjects (6 males and 5 females) having the attributes Health status = {S, I, R} and Sex = {Male, Female}. The sojourn time for the Infectious stage is drawn from a 3-Erlang(T/3) distribution, producing an average sojourn time T. The successive transformations between representations are also shown. An ABM or EBM is based on 11 subjects, a CBM is based on 10 compartments and an SBM is based on 34,020 situations. The transformation arrow “Û” means that two models can be transformed into each other by a 1:1 mapping without loss of information.
k ´ l ´ m. The attributes of the former entities are now handled by the stages containing tokens without any remaining attributes. These tokens can still be referenced. (In a general case, when an attribute takes continuous values, e.g. age, then the necessary discretisation into intervals would mean some loss of information.)
T5 (Stage to compartment expansion): The stage to compartment expansion (also called distribution expansion) is necessary because the individual tokens are anonymous. When a token enters a stage for a sojourn according to a specific sojourn time distribution, it is no longer possible to keep track of its sojourn in the stage. Furthermore, to allow mixing of newcomers and tokens that have been in a compartment for some time, it is mathematically necessary that the sojourn times in a compartment have a memoryless, i.e. exponential, sojourn time distribution. Therefore, the infectious stage must be represented by a structure of three serial compartments with the time constants T/3 to produce the intended 3-Erlang(T/3) sojourn time distribution of the infectious stage. The transformations T3, T4 and T5 take the EBM into a CBM. (In a general case, representing a given sojourn time distribution by a structure of compartments implies an approximation.)
T6 (Combinational expansion): Finally, a CBM with k physically interconnected compartments that is populated by n anonymous tokens can be in n + k − 1 over k − 1 discrete situations. In our example, we have two separate compartment chains for male and female tokens, respectively―although linked since a male can infect a female and vice versa. A graph or a situation vector (“state vector”) representing these situations can be used to represent all possible situations the total model can be in. By connecting these situations to describe possible transitions and by including the probabilities of each transition between pairs of situations, a “state”-transition graph is obtained. It is also possible to use a transition matrix composed of transition probabilities that can update the situation (“state”) vector over time. We now have an SBM.
Note, however, that if one starts by observing, measuring or estimating the individual transition probabilities of a transition graph (or matrix), then the assigned transition probabilities will lack the consistent couplings obtained if the SBS is derived from a CBM. This almost certainly implies that there will be no CBM that exactly corresponds to the SBM. (However, one can find a CBM that best, in e.g. a least squares sense, corresponds to the SBM.)
Thus, a representation can be obtained from a sequence of transformations. For example: the SBM representation can be derived as T6[T5[T4[T3[T2[T1[ABM representation]]]]]]. These transformations preserve consistency of results from ABM, EBM, CBM and SBM, provided that the transformations are properly performed.
In this example, all transitions except T4, where identity was dropped, and T6 are reversible (symbolised by two-way arrows). In fact if the SBM equals T6 [CBM] it is reversible, but an empirically obtained SBM usually has no exactly corresponding CBM. ■
In a general case, an attribute expansion of a continuous attribute will introduce some attribute discretisation error in T3. However, the discretisation error can be reduced by using a finer subdivision of attribute values. Moreover, the stage to compartment expansion T5, where a stage is represented by a structure of compartments to approximate the sojourn time distribution, is only exact for the Erlang type of distribution. Such an error can be made arbitrarily small at the expense of a more complex stage description.
4.2.5. Choice of a Proper Model Representation
How ABM & EBM, CBM and SBM grow in size for a modelled population of n subjects requiring k compartments is shown in Figure 5. The number of situations is in this case based on the assumption that each of the n subjects can populate any of the k compartments. Although the elements (agents, entities, compartments or situations) are different concepts from different model representations, the figure illustrates the number of main elements required for each representation.
The best model representation to choose can be a matter of size and time of execution. Obviously, in Example 1 above, the situation-based model with its situation vector of 34,020 elements for 11 subjects (and the transition matrix being the square of this number, although sparse) is not an attractive choice. Small situation-based models may be analytically treated, and the fact that the whole situation vector, representing the pdf of all situations, can be updated by matrix multiplication is an advantage for mathematical modelling. However, SBMs are
![]()
Figure 5. The number of components required for agent and entity-based (dashed line), compartment-based (dotted lines) and situation-based (solid lines) models of a population under study, where nsubjects require k interconnected compartments. The number of situations is based on the assumption that each of the n subjects can populate every of the k compartments.
awkward for simulation modelling, and they also have a number of additional disadvantages related to stochasticity and time handling [24] .
The choice between ABM, EBM and CBM has its pros and cons. From Figure 5, we see that the size of an ABM and an EBM both grow linearly with the size of the population under study, while a CBM remains constant in size. On the other hand, the number of compartments in a CBM grows multiplicatively with the number of possible values of each attribute, as well as with the complexity of stages (modelled as structures of compartments). These factors only marginally affect the complexity of agents or entities of an ABM or an EBM. The question of attributes is one of homogeneity; with few attributes to consider, we obtain a rather homogeneous population model, making a CBM an attractive option.
Another issue is whether identity must be preserved in the model. If this is the case, it will exclude the use of a CBM (and of an SBM).
The choice between ABM and EBM is often a matter of taste. However, procedural homogeneity (so that all subjects can use the same track system) makes an EBM attractive. An ABM, on the other hand, is a good choice if there are many types of subjects and if the modeller needs to write his or her own code that is not supported by the multitude of standard stages (stations) and transition mechanisms in an entity-based simulation language.
The type of question to be studied is also important. The use of an ABM or EBM offers the opportunity to add details, heterogeneity and complexity to the behaviour of the individuals and to study the consequences of these additions. However, complexity may also make it difficult to distinguish important patterns.
An ABM and an EBM describe the population on an individual level, while a CBM focuses on subpopulations having the same set of attribute values, which may be the level of the system under study we are interested in. In such a case, using an ABM or EBM to generate the subpopulations is a detour. For example, it is argued by Grimm [41] that in ecological models, “bottom-up approaches [individual-based models] alone will never lead to theories at the system level”, and that “state variable or top-down approaches [CBMs] are needed to provide an appropriate integrated view”.
The transformations introduced in Section 4.2.4 are important for translation between representations. They show how a CBM can be constructed consistently with a corresponding ABM, except that the possibility to track individuals is lost.
Furthermore, in Chapter 5 we show how a stochastic CBM can sometimes be approximated by continuous and deterministic flow models that are easier to analyse mathematically. Such an approximation results in loss of information, however.
4.3. Handling Uncertainties
A model is always a simplification because only the main components and relations important for the purpose are included. Full and exact information about the structure of the system under study and its behaviour is never available. Describing only the causal relations between different components of the system under study (as we understand it) provides a deterministic model. Compared with the behaviour of the deterministic model, the behaviour of the system under study will in many cases look somewhat irregular. However, there is information in these irregularities―even when they are too complex to understand and to model in detail―that can be at least partly reproduced by statistical distributions and can therefore be used in the model. Technically, this can be accomplished by describing the relevant statistical distribution and then using it in the generation of random numbers. We thereby obtain an irregularly behaving stochastic model of the system under study that will behave somewhat differently for each simulation run (replication).
4.3.1. Handling Different Types of Uncertainty
In our next example, we discuss where uncertainty can appear in discrete population modelling by considering the five types of uncertainty introduced in Chapter 3: Structural uncertainty, Transition uncertainty, Initial value uncertainty, Parameter uncertainty and Signal uncertainty. We then discuss how these types of uncertainty can be handled.
Example 2: Representation of uncertainties
An epidemic in a population system is studied by a model similar to that in Example 1, but with no sex attribute and where the sojourn time distribution in the infectious stage is uncertain. In addition, we include an authority that collects information about the number of infectious individuals and issues recommendations about avoiding contact and using sanitary measures, which affects the infection rate. This is shown in Figure 6. The model is used to demonstrate the locations of the uncertainties and how they can be handled in the model. Here we choose to use a CBM to demonstrate where and how these uncertainties can enter the model, although we could also have used an ABM or EBM.
Structural uncertainty about the system under study can be handled by alternative models. The uncertainty is then reflected by the difference in behaviour of these models.
The remaining four types of uncertainty are handled within the model by assigning probability distributions. By drawing random numbers from these distributions we introduce Transition, Initial value, Parameter and Signal stochasticities. We now have a stochastic model that behaves differently for each replication.
Technically, a compartment-based model is composed of stages, transitions, parameters and information links. Each of these composition elements can have its own type of uncertainty. Approximate information about the number of objects in the stages at time zero can motivate initial value stochasticities for S(0), I(0) and R(0). There is almost never enough information to decide the exact event times for transitions. Therefore, transition
![]() (a) (b)
(a) (b)
Figure 6. Example 2. (a) An infectious system under study and its environment. (b) Alternative epidemic models, the first of which is a SIR model based on the stages S, I and R (initiated to S0, I0 and R0), transitions F1and F2, and parameters p, T and Distortion. An “Authority”, collects information about the number of infectious individuals and issues recommendations, which affect the infection rate. Dice show where different types of stochasticities can be included.
stochasticity6 in the flows F1 and F2 is used to complement the dynamic description with the available statistical information for the transitions. Unexplained irregularly varying values of the parameters p, T and Distortion motivate the use of parameter stochasticity6 to generate realistic inputs from these parameters. Uncertainty about the delay of a signal can be described by signal stochasticity. The locations of the stochasticities are symbolised by dice in Figure 6(b).
The dashed rectangle in Figure 6(b) approximately represents the system under study in Figure 6(a). This core part of the model is the explained part, consisting of dynamic relations. This part may contain uncertainties in transitions of subjects or signals because of a high aggregation level.
The outer part of the model contains supplementary unexplained influences on the core part of the model that we have no intention to structurally model. Here we only describe the influences from the environment and the conditions at time zero as parameters and initial values, if necessary in statistical terms. ■
4.3.2. Handling Structural Uncertainty
The description of the SIR model in Example 2 is not complete. In particular, the time in the Infectious stage (the so-called sojourn time) is on average T time units. However, some individuals will recover sooner and others will require a longer time. By modelling the Infectious stage by a single compartment (as is done in “Structure 1” of Figure 6(b)), we implicitly assume an exponential sojourn time distribution. Other assumptions about this distribution can be realised by using several compartments in parallel and/or series.
Another structural possibility is that an infected individual does not immediately become infectious. The exposed individual may require a latent period before entering the Infectious stage. This can be accomplished by including an Exposed (E) stage between the Susceptible and the Infectious stages (giving a so-called SEIR model).
By studying the differences in outcomes (size of the epidemic, time until the last person recovers etc.) for the alternative models, it is possible to create an estimate about the contribution to uncertainty in the results that comes from structural uncertainty.
4.3.3. Handling Transition Uncertainty
Subjects can instantly change from one stage to another. The change of a subject is an event that takes place at a point in time called the event time. Such events may occur regularly or irregularly in time. The rate (number of events per time unit) of subjects transferred from one stage to another is called the intensity.
Transition uncertainty is handled by transition stochasticity. If we know the expected intensity, which may vary over time, then the number of independently occuring transitions during a short time step is obtained by drawing a “random” number from a Poisson distribution with the intensity as argument. (Equivalently, the interval between two successive transition events may be generated by drawing from an exponential distribution with a time parameter equal to the inverted value of the intensity.)
The expected intensity is in turn given by some expression where stochastic parameters (Parameter stochasticity) can also be included. See Figure 6(b).
A transition event takes a different expression in different representations.
For an agent-based model, a transition event will change the value of the stage attribute of a specific agent.
For an entity-based model, a transition event will change the stage of a specific entity.
In a compartment-based model, anonymous subjects are transferred from one stage to another. When a stage is expanded into a structure of compartments, there will also be internal stochastic transitions between the compartments representing the stage.
In a situation-based model, a situation refers to the entire model, so an event affecting any subject will take the model from one situation to another.
Transition stochasticity is the driving force in a stochastic discrete model. Without the irregularly occurring transition events, no development over time will take place in such a model. Thus, the transition stochasticity generates both the dynamics of the model and the stochastic development in an inseparable way7.
The technical realisation of transition stochasticity depends on the time handling principle used. Because time handling is not treated until Section 4.5, the technical realisation of transition stochasticity is discussed in that section and in an example in Appendix A.
4.3.4. Handling Initial Value Uncertainty
Uncertainty about initial values can be handled by generating variability of the initial conditions in repeated simulation runs (replications). Initial value stochasticity is then used before the start of the execution and does not intervene during the simulation.
Consideration of initial value stochasticity is important whenever the initial situation of a studied process is unclear because of inaccurate information. For example, will the next epidemic start from a single infectious individual or from a batch of infectious individuals returning from abroad?
A good example where initial value stochasticity is crucial is a randomised medical trial, in which one group of n cases is exposed to a chemical substance and another group of m reference cases remains unexposed. These groups are randomly sampled from a large population to study the risk of developing a certain disease during a follow-up period. However, assume that a known fraction p of the population already has the disease, although not yet diagnosed. In the model, the exposed and unexposed groups must then be initialised by n − Binomial [n, p] and m − Binomial[m, p] healthy subjects, in order to consider the objects initially having the disease. Otherwise, the results will be biased and the variations between replications and thus the resulting confidence intervals around the results will become too small. (Binomial[…] means a random number drawn from a Binomial(…) distribution.)
The technical realisation of initial value stochasticity is the same for different time handling methods.
4.3.5. Handling Parameter Uncertainty
Uncertainty about parameter values can be handled by parameter stochasticity. Unlike transition stochasticity, which is intrinsic in the time handling method and is statistically completely specified to its form, parameter stochasticity is used to describe the lack of knowledge about how the environment affects the system under study. This lack of knowledge may be about unknown constants or about unexplained variations that we perceive as irregularities. Such irregularities may be variations in temperature, wind, precipitation, food supply, pollution, fertility, noise or disturbances of any kind. To include information about external irregularities, these either have to be generated by an adequate sub-model (which is often not possible) or the unexplained irregularities have to be described by appropriate, often empirical, statistical distributions.
Parameter stochasticities are introduced in the parameters by making them stochastic. This is shown in the SIR model example in Figure 6(b) by placing the risk parameter, p, and the sojourn time parameter, T, in the outer part of the model as parameter inputs to the model. Thus, for a population model, parameter stochasticity will affect the development indirectly, via parameters that in turn influence the transition probabilities.
Technically, the values of parameters describing e.g. migration, morbidity, mortality, fertility, risk, sojourn time etc. have to be drawn from an appropriate statistical distribution during the simulation run. When a parameter is constant but unknown, it resembles the initial value case, requiring only one random sample from a statistical distribution before the onset of the simulation run. However, when the parameter changes irregularly over time (e.g. temperature or precipitation) there are two stochastic aspects involved: “When to change the parameter?” and “What is the new value?”. Samples from two random number generators, with in general different distributions, are then required.
There is no difference in coding parameter stochasticity in agent-based, entity-based and compartment-based modelling. However, a situation-based model, e.g. a Markov model, is based on transition probabilities that take the entire model from one situation (state) to another. These transition probabilities merge exogenous parameters with the time step and other factors into a number in a very complicated way that considers all possible ways of going from one situation to another. In practice, it would usually be extremely complicated to include parameter stochasticity in a situation-based model, not only because an exogenous parameter is not a concept in this type of model, but also because the transition probability matrix must be updated (recalculated) whenever a parameter value is changed.
4.3.6. Handling Signal Uncertainty
Before we discuss signal uncertainty, we have to clarify that information links in a model can be of two different types:
1) Artificial information link―a technical concept to communicate logic between artificially separated model parts. For example when a radioactive atom decays, there is one radioactive atom less in the system under study. In a compartment-based model this is accomplished by construction of a compartment and a physical outflow. An artificial link from the compartment to the valve regulating the outflow also has to be included. Its only function is to transfer information from the compartment equation to the flow equation. There is no counterpart to such a link in the system under study, and no uncertainty or delay can be involved.
2) Signal link―a description of a real information link that communicates information in the system under study. We call this communicated information “signal”. A signal can be distorted and delayed.
In Figure 6(b), the information links above the physical flows are artificial, but required to communicate information to the logics regulating the physical flows. This “logical information” is immediate, intrinsic and cannot be affected by disturbances. Artificial information links are most obvious in compartment-based models. In agent- and entity-based models there is no division between state and flow. Attributes or common parameters are here updated by programme logic that is intrinsic, and not a separable part in the system under study.
However, below the physical flows in Figure 6(b) a real authority that collects information about the number of infectious individuals and issues recommendations in order to reduce the infection rate is modelled. Here signals from the Infectious compartment to “Authority” and from “Authority” to the transition flow, F1, describe real information flows (signals) in the system under study. These signals require time to reach the receiver that may vary in an unpredictable way (the information is sent by post, it may not be delivered during the weekend, recommendations are sent to the media and consumed at different times by the Susceptibles) and the information may be distorted for various reasons (imperfect information, typing error, distortion of the signal, misinterpretation, not reaching all subjects). When it is not known exactly for how long a message will be delayed or if and how it is distorted, we may have to use a stochastic description when a delay or distortion of the signal will create other effects than a prompt and undisturbed signal.
Delays can be generated as sojourn times drawn from a proper distribution and distortion of the signal may be treated as parameter stochasticity (as “Authority” in Figure 6(b)). In this way, uncertainty about signals can be handled by signal stochasticity.
4.3.7. Correlations in Parameters and Initial Values
When observing a time series of n successive measurements {pi} for i = 1, …, n, it is often the case that observations a short time apart show a (positive or negative) autocorrelation with each other. For example, the weather, price on the stock market or prevalence of influenza one day may be similar to that on the previous day. Sequences of auto-correlated parameter values can be obtained for example by weighting together a new random sample with previous random samples.
There may also be (positive or negative) cross-correlation between two time series {pi} and {qi} for i = 1, …, n. For example if pi represents amount of sunshine and qi represents amount of precipitation, there is a strong negative cross-correlation during daytime. The cross-correlation may also refer to some quantity, e.g. temperature, observed at two nearby geographical locations. Cross-correlation requires the use of joint (multivariate) distributions from which to draw the “random” numbers.
Parameter stochasticity may require a description of autocorrelations or cross-correlations, while initial value stochasticity may require the use of cross-correlation.
Transition stochasticity directly affects the stochastic variations, as well as correlations for stages.
A stochastic population model where the structure of the system under study is preserved will often recreate the proper dynamics, including correlations. In e.g. a prey-predator model [43] - [45] , a time-varying cross-cor- relation between the number of prey and predators is generated by the model structure.
When additional correlated factors outside the system border also affect the transitions, the expected intensities li can be modelled as functions of corresponding auto- or cross-correlated parameters pj. The externally correlated intensities li(pj) will then be part of the transition equations, which have a somewhat different expression depending on the time handling principle chosen, see Section 4.5. The SIR model shown in Figure 6(b) provides an example of this if the parameters p and T are correlated. (Old people may have a higher risk p and a longer time T when they are infectious.)
For a black-box model, which only aims to recreate the input to output relationship without knowing the structure of the system under study, designing a model that has prescribed correlation properties is a very complicated problem and there is no generally applicable method for nonlinear models. Cross-correlations between time series and autocorrelations within time series that are generated by a dynamic model may be generated by the dynamics (feedback loops, couplings and time lags). Correlations may also be introduced between different flows affected by one (time-varying) parameter.
4.4. Output Function
The model has to be extended to quantitatively express the purpose of the study as one or more output functions expressed in model terms. For example, for a model aiming to maximise the profit or minimise the costs on an animal farm, the system may consist of the different animals and some equipment, feed etc. An output function that expresses the profit or costs in terms of these model components must then be added.
4.5. Time Handling Principles
Time handling concerns the recalculation mechanism used to advance a model through simulated time, thereby creating the dynamic model development. It is a method for updating both deterministic and stochastic parts of a model over simulated time. However, here we pay extra attention to transition stochasticity, because dynamics and transition stochastics are inseparable aspects of transitions.
4.5.1. The Poisson Process and the Poisson Distribution
The Poisson process describes randomly occurring events in a flexible way, see e.g. [46] . This process is fundamental to understanding time handling for the transitions in a discrete stochastic model. The process is an integer-valued continuous time counting process that can be used to describe random events that happen with a specific intensity l per unit time. It can also accommodate a varying intensity, l (...), which in turn can be expressed as a function of any quantity in the model; e.g. attribute values, other transitions, parameters (that may be stochastic and even auto- or cross-correlated) and time.
Definition of a stationary Poisson process: Let the non-negative integer N(t), t ³ 0 be the number of times an event E occurs in a time interval (0, T). If the stochastic process {N(t), t ³ 0} possesses the properties:
The process has independent increments, (1)
 (2)
(2)
 (3)
(3)
then the process is a stationary Poisson process with intensity l. ■
For our purposes, the stationary Poisson process must be generalised in two ways:
First, condition (1) “independent increments”, means that the events must be mutually independent. This is not always the case for transitions in a population under study. For example, commodities may be produced in batches, couples come together or groups are formed for different reasons. Such cases are usually handled in the model logic by forming batches, couples, groups etc. that go together as a unit in the transition to a new attribute, stage or situation, without affecting the underlying time handling mechanism.
Second, the Poisson process may need to have a time variable intensity (l = l(t)). This would give condition (2) the form: P[E occurs exactly once during (t, t + h)] = l(t)∙h + o(h). However, the Poisson process with a time variable intensity l(t) can be approximated by a stepwise constant l during each time interval (t, t + h) for a sufficiently short time increment h. For our purpose, it is therefore sufficient to stay with a piecewise stationary Poisson process.
For a stationary Poisson process, the number of events that might occur during a time interval, Dt, which is not necessarily very short, is Poisson distributed. In fact, randomly and independently occurring events with intensity l during an interval of length Dt will produce a Poisson-distributed number of events with the argument Dt∙l. The Poisson distribution is then symbolically written as Po(Dt∙l).
The Poisson distribution has a number of important properties [46] :
1) If X is Po(Dt∙l), then the expected value of X is Dt∙l and the variance is also Dt∙l.
2) If X is Po(Dt∙l1) and Y is Po(Dt∙l2), where X and Y are independent, then X + Y is Po(Dt∙l1 + Dt∙l2).
3) When the events of a Poisson process have intensity l, the time intervals between events are Exp(1/l) distributed. This also implies that independent events from two processes with intensities l1 and l2 will have Exp(1/(l1 + l2))-distributed time intervals between events from any of the processes.
4.5.2. Time Handling Strategies
Irrespective of the type of model representation, there are three possible time handling strategies for a stochastic model:
1) Micro Time Slicing, which slices time into such small intervals (t, t + dt) that the probability of more than one event in a time slice of length dt is negligible.
2) Time Slicing, where several events may occur in the time interval (t, t + Dt).
3) Event Scheduling, where time is advanced from event time ti to the point in time ti+1 for the next event.
For all three methods, it is important that the step size is not so large that the model changes its dynamic behaviour significantly during the time step. More precisely, the time step should be sufficiently short so that the conditions of the model can be regarded as stationary during the time step. These methods can then be used also in the time varying case by regarding the process as piecewise stationary within each time step.
The three alternative ways of generating time sequences of irregularly occurring events from a Poisson process with a (stepwise) stationary intensity of l events per time unit are illustrated in Figure 7. The realisations of transition stochasticity using Micro Time Slicing, Time Slicing and Event Scheduling are treated in Appendix A.
Any of the three time handling methods can be implemented into agent-, entity-, compartment- or situation- based models, producing consistent (contradiction-free) results. As can be seen from Figure 7, the three time handling methods make use of different statistical distributions (Bernoulli, Poisson, exponential) to model the transitions that change the attribute values, stages, compartment contents or situations.
Micro Time Slicing:
Micro Time Slicing advances time by very small increments, dt. Bernoulli-distributed statistics are then used to decide if zero or one event will occur during (t, t + dt).
According to the definition of the stationary Poisson process, the probability of an event occurring during a very short time interval is proportional to the length of the interval and to the intensity of events l, i.e. Bernoulli (dt∙l). The probability of more than one event occurring during (t, t + dt) is then regarded as negligible; ordo (dt). In a numerical setting, the Bernoulli (dt∙l) distribution is used to decide whether an event will happen during (t, t + dt). Occurring events can then be regarded as a sequence of points in time where single events that happen are handled within these time increments.
Micro Time Slicing is a very inefficient way of handling time, because dt has to be so short that more than one event should almost never occur in the system during (t, t + dt). If several events should sometimes occur in the system under study during (t, t + dt), the Micro Time Slicing method is limited to never reproducing more than one of these events. Furthermore, the very short time step dt required implies that the vast majority of the intervals will be empty, which makes simulation extremely inefficient and the execution time unnecessarily long. In simulation, Micro Time Slicing is relevant only to make situation-based models simple to implement.
Time Slicing:
Time Slicing advances time by a considerable time step (Dt) that is large enough to permit several events to occur, yet small enough so that the dynamic conditions (summarised by the intensity l(t)) are insignificantly altered during the time step. (The duration of the time step may even be varied during the simulation to accom- modate the dynamics varying over time.) The number of events during Dt is then Po(Dt∙l) distributed. During a
![]()
Figure 7. A stationary Poisson process with intensity l can be generated in different ways. Events of a Poisson process are marked “´” on the time axis. For Micro Time Slicing, the probability of an event during (t, t + dt) is Bernoulli (dt∙l) distributed. For Time Slicing, the probability of k events during (t, t + Dt) is Poisson(Dt∙l) distributed. For Event Scheduling, the time between successive events is Exp(1/l) distributed. Different random number generators based on these distributions are therefore used depending on the chosen time handling method.
simulation, the number of events is obtained from a Poisson-distributed random number generator, where the value Dt∙l is specified as argument.
Deterministic compartment-based models, described by differential or difference equations, traditionally use Time Slicing. Time Slicing can also be used for stochastic compartment-based models. This approach was first described by Gustafsson in 2000 [13] under the name “Poisson Simulation”, and in the following year by Gillespie [47] under the name “tau-leaping”. (The tau is the Dt leaping over many events.) A great advantage is that Continuous System Simulation Languages can thereby be used also for stochastic compartment-based models. A brief presentation of stochastic compartment-based modelling using the Poisson Simulation approach is given in Appendix B. See also [23] . Constructions like queues of different kinds can easily be accomplished within compartment-based modelling by using Poisson Simulation, see [14] .
Time Slicing can also be used in agent-based and entity-based modelling. Then each agent or entity will test for an event to happen during each time step. This results in a Poisson-distributed number of events taking place during the time step―although no Poisson-distributed random number generator will be involved. For e.g. an agent- or entity-based SIR model, Time Slicing will avoid the complication of using event scheduling (see below) when the intensity of e.g. an epidemic increases drastically.
In principle, Time Slicing can be used also in situation-based modelling, although then the functions that generate the transition probabilities between situations can become extremely complex.
Event Scheduling:
Event Scheduling advances time to the instant of the next event. Then exactly one event is handled per time step.
The durations between successive random events of a stationary Poisson process with intensity l are exponentially distributed according to Exp(1/l). By drawing a number from a random number generator with this distribution, the next event is scheduled at tnext := tnow+ Exp[1/lnow]. (A random number drawn from a distribution Distrib(…) will be denoted Distrib[…] using brackets. Further, the symbol := is used for assignment.) Each event generates a change in the model. Between consecutive events, no change is assumed to occur, so the model will directly jump from one event to the next [5] [34] [48] .
This time handling scheme is much more efficient than updating by infinitesimally small time steps dt, although slow when there are very many events during a simulation. Another advantage is that there is no (artificial) time step to adjust.
However, the uncontrolled duration of the inter-event time in Event Scheduling may create a problem. If the time interval to the next event, Exp[1/l], is so long that the intensity of events will change considerably because of internal or external conditions, a problem may arise. For example, if the intensity l(t1) of customers arriving at a restaurant is very low at time t1 (before lunch), then the next customer, scheduled to arrive at t2 := t1 + Exp[1/l(t1)] may come late in the afternoon, meaning that the rush of lunch customers will be missed. This problem can be handled by e.g. techniques for over-sampling and thinning [5] [34] [49] . The event-scheduling algorithm is sometimes falsely called an “exact” integration method, but this is only true for models where the internal and external conditions do not change.
Event Scheduling is often used in agent-based and entity-based simulation. However, direct programming of events related to different types of agents or entities will result in a spaghetti-like programme code. Therefore, a method called pseudo-parallel execution has been developed where the scheduled departure time of an agent or entity (or an arrival time for the next agent or entity) of the same type is coded within the agent or entity) [12] .
For compartment-based simulation, the first stochastic time handling algorithm was an event-scheduling method presented by Daniel Gillespie [50] , which is known as the Stochastic Simulation Algorithm (SSA). This algorithm first uses property 3) of the Poisson distribution above to find the next (overall) event by drawing a random number from an Exp(1/(l1 + l2 + ...)) distribution. It then draws a second random number from a uniform distribution to decide in which process the event occurs.
For situation-based simulation, the method of exponentially distributed time increments gives a simpler model structure and significantly speeds up the simulation compared with using a short fixed time step dt. However, it requires the model to be defined for continuous time rather than for discrete, equally spaced points in time. In situation-based modelling, a process using next event scheduling is called a jump process; see [36] .
4.6. Start and Termination Criteria
The calculations proceed stepwise over time from a start time until a termination criterion is satisfied.
4.6.1. The Start Time
The start time is usually a predefined point in time, e.g. 1 January 2016, but it can also be the point in time when a specific event occurs in order to study the consequences of this event. The model may also be run for a warm-up period, e.g. to reach a stationary state from where the real replication is started. In some studies, the start time can be e.g. the time of diagnosis for a disease to be followed, which varies in time for different members in a cohort under study. The “time zero” of the simulated time then refers to different real times for different objects in the system under study. However, if there are interactions between the objects, then the subjects have to be synchronised to a common simulated time axis.
4.6.2. Termination Criterion
The termination (stop, break) criterion, specifying when the replication is to be completed, needs to be defined. The termination criterion can be of two kinds:
1) A definite (fixed time) termination criterion.
2) An indefinite (conditional) criterion based on some condition (other than “a fixed termination time”) to occur in the model. For example in a stochastic model, termination could be when a species becomes extinct. The termination time will then happen at different points in time for different replications.
The use of an indefinite (conditional) criterion can sometimes result in a large reduction in the execution time. For example when studying a stochastic SIR model [39] using a fixed time criterion, the termination time set must be sufficiently large to cover even the longest possible epidemic. The execution time can then be drastically reduced by using: “If Number_of_infectious = 0 then Terminate” because when there are no infectious subjects left, the epidemic is over.
5. The Continuous Simulation Model
Continuous population modelling means that the objects in the system under study are described as a continuous substance. This has a number of consequences for representation, stochasticity and time handling, but also for the behaviour of the model. Choosing a continuous rather than a discrete description of the population system entails a large simplification where a number of options for representation, uncertainties in transitions and choices of time handling method disappear. This is described in Section 5.1.
However, a continuous population model is often an oversimplification that hides important information and insights, prohibits possible phenomena such as extinction from occurring, removes stochastic variations from transitions and often distorts the model behaviour and introduces bias in estimates. In Section 5.2, possible distortions from using a simplified continuous population model are exemplified and discussed. In Section 5.3, conditions are presented for a continuous population model to produce unbiased point estimates. Finally, in Section 5.4 we discuss the great advantages of using a continuous population model when it is justified.
5.1. The Simplified Anatomy of Continuous Models
In a continuous model, the objects are modelled as infinitely divisible and are quantified by real numbers. The continuous substance is also gradually transferred between stages (representing sets of attribute values), replacing the concept of specific events in time. This leads to a number of consequences as shown in Figure 8, where options under points 2, 3 and 5 vanish compared with the discrete model category shown in Figure 1.
Below we briefly discuss the “anatomical” issues (2) to (6).
(2) The description of a population as a continuous substance reduces the number of feasible representations. Of course agent-based and entity-based representations are not possible for the continuous model category of models.
Situation-based models such as Markov chain models will also vanish because the real-valued (instead of integer-valued) contents of underlying compartments would create infinitely many situations. Only a compartment-based representation can be used. In the continuous case, the contents of the compartments are real valued instead of integer valued.
(3) Although a continuous population model can be based on an uncertain structure and contain initial value uncertainty and parameter uncertainty, the transition uncertainty will vanish in the continuous approximation.
This is easy to see, because a continuous substance can be regarded as composed of infinitely many infinitesimal entities. Now assume that the flow transferred during a time step consists of m entities, then the number of
![]()
Figure 8. For the continuous simulation model, a number of options vanish. Compare with Figure 1.
transitions is Poisson distributed according to Po(m). However, Po(m) approaches the normal distribution Normal(m,Öm) for large m. This means that the relative variation (standard deviation/expected value: Öm/m = 1/Öm) approaches zero when m increases, i.e. the transition stochasticity vanishes. This does not mean that the flows (with intensity l) cannot be irregular, but the irregularities then come from unexplained parameter variations affecting the transition intensity l(p(t)), not from transition stochasticity.
Note that a continuous model is not the same as a deterministic model, because continuous substance does not eliminate initial value stochasticity and parameter stochasticity. A deterministic model is just a special case where there is no stochasticity of any kind.
(4) The output function is only indirectly affected in that it has to be expressed in continuous instead of discrete variables of populations or subpopulations. This may for example significantly simplify optimisation (including parameter estimation), since numerical search methods can be used. Optimisation is considerably faster and simpler to treat for the continuous case than for the discrete case.
(5) The time handling options are affected in a continuous model because the continuous substance “flows” gradually between compartments, so there are no (or infinitely many) events. The Event Scheduling approach then disappears as an option. Time Slicing can be used. A very small time step can be used if desired, but Micro Time Slicing would be a pointless concept in the continuous case. The flow would still be continuous for arbitrary small time steps.
(6) Finally, the termination criterion can be definite or indefinite. However, the use of an indefinite termination criterion in a continuous model may create bias even when a definite termination criterion will not. This is illustrated in Example 2 in Chapter 4 in [22] .
5.2. Possible Distortions from Using a Simplified Continuous Population Model
Before discussing problems that might occur because of using a continuous population model, we illustrate the loss of insight and information by comparing the model behaviours of discrete (containing transition stochasticity) and continuous population models.
Example 3: The behaviours of discrete and continuous population models
We now demonstrate that continuous modelling removes many of the characteristics of a population system. We do this by showing that three fundamentally different discrete population models can behave identically when using the continuous model category. To make the example lucid, these models do not include parameter or initial value stochasticities.
A) First, consider a stochastic logistic growth model with a size of x(t) subjects:
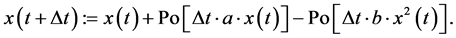
This is an open, first order non-linear model. The model structure and its behaviours from three replications are shown in Figure 9, where the number of subjects continues to fluctuate over time with large variations (with the risk of extinction).
B) Next, consider a stochastic epidemic SI model of N = S + I subjects, where a susceptible set (S) is infected by encounters with members of an infectious set (I). The risk of infection per time unit is proportional to the number of susceptibles, to the number of infectious subjects and to a constant c. Thus:
![]()
![]()
![]()
This is a closed, second order bilinear model, shown in Figure 10, where the number of infectious subjects increases stepwise to N = S + I, where it remains.
![]()
Figure 9. A Forrester diagram [51] of a stochastic logistic model and the results of three replications of the model for the case a = 0.1, b = 0.01 and x(0) = 1.
![]()
Figure 10. A Forrester diagram of the stochastic SI model and three replications of its behaviour. (Results for c = 0.01, S(0) = 9 and I(0) = 1.)
C) Finally, consider a stochastic pruned prey-predator model where prey births and predator deaths are removed:
![]()
![]()
![]()
![]()
![]()
This consists of two open and coupled first order submodels, shown in Figure 11, where the number of predators increases stepwise to an undefined final level.
Now, we eliminate the transition stochasticity from the three models by removing the Po[ ] parts. We then obtain the corresponding deterministic model that is embedded in the stochastic model. We also use differential equations by letting Dt approach zero.
a) The deterministic logistic model then takes the form: dx/dt = a∙x − b∙x2.
b) The deterministic SI model, where S is denoted y and I is denoted x, takes the form:
![]() (4)
(4)
![]() (5)
(5)
Since x + y = N in a closed model, we can insert y = N − x in Equation (5), giving: ![]() . As seen, for c = b and N = a/b we get exactly the logistic equation in Example 3a.
. As seen, for c = b and N = a/b we get exactly the logistic equation in Example 3a.
c) The deterministic pruned prey-predator model, where PREY is denoted by y and PRED is denoted by x, then takes the form:
![]() (6)
(6)
![]() (7)
(7)
However, with d = e = c equations (6) and (7) are identical to Equations (4) and (5) in Example 3b, which in turn (for c = b and N = a/b) are identical to the logistic equation in Example 3a.
In Figure 12, the three deterministic models and their identical behaviours are shown.
As seen in Figure 12, the continuous approach removes all the differences between the behaviours of the three
![]()
Figure 11. A Forrester diagram of the stochastic pruned prey-predator model and three replications showing possible model behaviours of the predators. (Results for d = e = 0.01, PREY(0) = 9 and PRED(0) = 1.)
![]()
Figure 12. A Forrester diagram of the deterministic logistic model, the deterministic SI model and the deterministic pruned prey-predator model, with the same parameter values and initial conditions as in the stochastic cases. The behaviours of these deterministic models are identical.
models by eliminating the variability created by transition stochasticity. It also introduces bias in the results. Finally, it does not capture the risk of extinction in Example 3A) if, for example, the first event is death of the only subject initialised at time zero. ■
The example above shows that much information about a model’s behaviour is eliminated by removing the discreteness, and thereby the transition stochasticity. Depending on the system under study and the purpose, this may have great consequences for the results and conclusions.
When transition stochasticity is omitted in a population model, various types of distortions may occur. For example:
Information about irregular variations and the possibility to calculate confidence intervals is lost.
The omission of an irregular transition rate may introduce bias in the average behaviour and result in biased estimates.
The lack of irregular transition rates may prevent queues from building up.
A deterministic model produces categorical answers, e.g. that X will win over Y, whereas a stochastic model will give the probabilities of X and Y as winners.
Important phenomena, such as extinction of a species or elimination of an epidemic, which can happen in the system under study and are reflected in stochastic modelling, can be lost.
Oscillations might disappear when they are not excited by transition stochasticity.
The termination time when using an indefinite termination criterion (correctly) varies between replications in a discrete population model, but is the same in a continuous deterministic model. This can introduce biased estimates.
Using a continuous deterministic population model means that only average estimates can be obtained. Unless this average (almost) equals the expected value obtained by a corresponding discrete and stochastic model, the use of a continuous model is not justified. All the points above may cause such a bias.
Understanding the behaviours and properties of a population system under study and what to preserve in a model to prevent distortion of the results is an important but complicated and deceitful issue. A detailed discussion of this issue, supplemented with a number of examples, is given in [22] .
5.3. When Are Consistent Results Obtained from a Continuous Model?
If the results from a continuous population model agree with the expected value (or average for a large number of replications) of those from a discrete model, we can say that the results from the continuous model are unbiased or consistent (contradiction-free). In this subsection we assume that the discrete model only contains transition stochasticity, which is removed in a corresponding embedded continuous model.
The question of when transition stochasticity can be removed is investigated in [22] , using compartment- based models. Here, the contents of the compartments are denoted state variables. The main results are that there are two cases in which deterministic models produce unbiased state variables:
1) Asymptotically, in the limit of large flows, dynamic models with stable locally linearised dynamics will not generate bias in state variables.
2) Linear dynamic models will not introduce bias in state variables as long as all state variables remain non-negative in both the deterministic and the stochastic models.
In both cases, non-biasedness also requires that the simulation be performed over a fixed time interval. For example, a sample of radioactive atoms will decay according to the linear and non-negative equation x(t + Dt) := x(t) − Po[Dt∙x(t)/T]/Dt, which on average will equal x(t + Dt) := x(t) − Dt∙x(t)/T over any fixed time interval. However, the time to extinction is varying but finite in the first case, but infinite in the second case.
The purpose of a study is related to one or more output functions. Unbiased results are obtained from an output function when the state variables are bias-free, if the output function is a linear expression of the state variables.
From a practical point of view, we recommend starting by building both a discrete and a continuous model, and then investigating whether the consequences of using a continuous model are acceptable in the particular case under study. If this is the case, then a continuous model may be preferable or it can be used for parameter estimation, sensitivity analysis and optimisation, without otherwise replacing the discrete and stochastic model.
5.4. Advantages of Using a Deterministic and Continuous Model When Justifiable
A simpler model is easier to comprehend, easier to construct and easier to validate. It entails a lower risk of unintended mistakes in programming and interpretation of the model results, and it usually executes faster. If a continuous model can replace a stochastic discrete model without distorting the results required by the purpose of the study, much simplification can be obtained.
First, if there are no initial, parameter or signal stochasticities involved in the continuous model, we have a deterministic continuous model. Then the full model study (of a specific case) is accomplished by a single replication, while a stochastic model requires a large number of replications to build the probability distribution/density functions (pdfs) of the result variables of interest.
Second, the gain from using more powerful higher order integration methods can be large for deterministic continuous models. The gain from using such integration routines vanishes, or at least is very marginal, when stochastics is involved. Furthermore, the execution of a replication of the continuous model is faster than for a stochastic model because there are fewer or no calls to random number generators.
Third, parameter estimation, optimisation and sensitivity analysis become much easier to perform on a deterministic model than on a stochastic model. For parameter estimation and optimisation in particular, where many sets of parameter values must be tested, many replications are required already for a deterministic model. For a stochastic model, each of these many replications must be replaced by e.g. hundreds of replications to find an approximate average estimate, often making the task very complicated and time-consuming. Therefore, it is easier and faster to perform the optimisation or parameter fitting on a continuous (and deterministic) model. The estimated values of the parameters can then be used in the corresponding stochastic model (provided they are unbiased).
Finally, a deterministic continuous model can often, at least partly, be mathematically treated and understood. In very simple cases the results can be presented as a formula. For example, equilibrium results may be obtained by setting derivatives to zero.
6. The Combined Simulation Model
Combined models that include both discrete subjects and continuous substances have a long tradition. At the very beginning of digital computer simulation, this technique was utilised by connecting an analogue computer solving ordinary differential equations and a digital computer handling the discrete subjects. This was called hybrid simulation. Later on, the digital computer was used for both tasks; “combined simulation”.
A technical problem in the model category of combined models is combining the concepts from the discrete and continuous models in the form of a combined Discrete Event Simulation (DES) and Continuous System Simulation (CSS) model. For example, different time handling principles such as Event Scheduling for the DES part and Time Slicing for the CSS part have to be synchronised. A short and well-formulated characterisation of CSS, DES and combined simulation is given by Kreutzer in [4] .
Many of the applications of combined simulation are outside the scope of population models. For population models, there may be a situation where it is appropriate to model some populations as discrete subjects and others as continuous substance. We then get a model of interaction between lateral model parts that describe populations using different model categories. Another situation is where we want to model the objects as well as internal processes of the objects. This is usually accomplished by describing the properties and behaviours of the object by subjects with attributes and procedures in a proper representation. However, in more complicated cases, it may be appropriate to use a hierarchical structure where the subjects are on the top level and each subject has one or more procedures that requires its own dynamic sub-model. Below, we briefly exemplify these two possibilities.
6.1. Laterally Combined Model
When a discrete approach is necessary, but the identities of the subjects are not crucial for the purpose of the study, the discrete and continuous models can both be handled in a unified way using Poisson Simulation [13] . A stochastic compartment-based model using the Poisson Simulation approach is briefly presented in Appendix B.
Example 4: A discrete and a combined prey-predator model
A stochastic prey-predator model treats prey (X) and predators (Y) in a compartment-based model as anonymous subjects, where the number of transitions is obtained by Poisson statistics:
![]()
![]()
![]()
![]()
![]()
![]()
Here a, b, c, d are parameters and X, Y are contents of the two compartments. (For pedagogical reasons, we have included Dt in both sides of the flow equations. We could have written Xbirths := Po[Dt∙a∙X]/Dt etc.)
By removing the Po[ ] part of the flow equations, but keeping the arguments, we obtain the traditional prey-predator model with continuous quantities. Thus we have two corresponding models; one discrete with transition stochastics and one continuous that is embedded in the former. This was discussed in Chapter 5.
However, it is also possible to build a combined model where the preys X (e.g. grass) are modelled as continuous and the predators Y (e.g. sheep) are discrete:
![]()
![]()
![]()
![]()
![]()
![]()
In this way we can build a laterally combined model within the same compartment-based representation and the same time handling method (Time Slicing) in such a simple and straightforward way that the combined model can easily be implemented in any Continuous System Simulation Language or general purpose programming language. See also [52] . ■
6.2. Hierarchically Combined Model
An example of a hierarchically combined population model may be a model, where subjects must be described by agents or entities to preserve their identities, and where we want to model internal processes within the objects, for example the development of a disease, by differential equations. For example, a vector x of continuous attributes might be updated by procedures, e.g. by differential equations dx/dt = f(x,t), and then discretised, to generate discrete attribute values. Such a model may be driven by a discrete event simulator using event scheduling, which includes a differential equation solver whose time handling is in some way synchronised with that of the discrete event simulator. Early examples of simulation packages that can do this are described in [53] - [55] .
The anatomy of a combined model thus consists of concepts from the discrete world mixed with concepts from the continuous model world, which have been treated in Chapters 4 and 5 above.
7. Summary and Discussion
7.1. Summary of Guidelines
In a shortened and simplified form, this guide suggests the following for the model-building phase of a population study.
1. Model category: The first choice is discrete mapping of the objects in the population under study into discrete subjects. Choosing a continuous model means that transition stochasticity is eliminated, which may introduce bias, eliminate oscillations or extinction, and eliminate or reduce all estimates of variations. If the purpose of the study is compatible with a continuous approach, we recommend starting by building both a discrete and a stochastic model, and then investigating if the consequences of using continuous approximations are acceptable in the particular study. If this is the case, then a continuous model may be preferable. A continuous and deterministic version of the model, if it produces unbiased results, can also be a great complement to the discrete model for subtasks such as parameter estimation, optimisation and sensitivity analysis.
2. Representation: If there is no need to follow individuals, a CBM is often the most convenient and efficient choice. A compartment model also has the advantages of: a) remaining constant in terms of number of compartments, irrespective of the size of the population under study (see Figure 5); b) including an embedded continuous model; and c) only requiring data on population or subpopulation level. However, when many attributes are involved and when the stages require complex structures of compartments to create realistic sojourn time distributions, an ABM or EBM may be preferable.
An ABM is usually preferable to an EBM when several types of objects, or objects with diverse procedures, are to be modelled.
3. Handling uncertainties: Structural uncertainty is best handled by comparing the results from alternative models, while the other types of uncertainty are handled by statistical distributions and random number generators, making the model stochastic.
Transition uncertainty is almost mandatory in population modelling. However, parameter and initial value uncertainty may also be crucial. For an SBM, the parameters are implicitly spread over the matrix of transition elements, so parameter uncertainty is much more complicated to implement and the transition elements have to be recalculated for each change of the parameter values. Any failure to describe an uncertainty will falsely narrow confidence intervals and may also introduce bias in the results.
4. Output function: The output function is a quantification of the purpose of the study that must be expressed in the terms used in the model, which in turn depends on the choice of representation. If the focus is on the individuals, e.g. min or max transition times or waiting times are crucial, then CBM and SBM cannot deliver, since the individuals are not observable.
5. Time handling: For CBM, Time Slicing is often a natural choice, but Event Scheduling is also rather efficient, if a bit awkward for models with many flows. For ABM and EBM, Event Scheduling is usually the standard choice. However, when intensity may rise drastically (e.g. the number of infections per unit time in a SIR model), Time Slicing is simpler to use.
An SBM traditionally uses Micro Time Slicing, which is awkward. However, Event Scheduling can also be used (e.g. jump Markov models).
6. Termination criterion: A definite termination criterion is often used in simulation. However, for some models, using an indefinite criterion can save much execution time. In e.g. a SIR model, the epidemic is over when the infectious stage becomes empty.
7.2. Discussion
The conceptual framework for population modelling for simulation that is presented here has evolved over a number of years. It grew from research on more efficient simulation methods for population models, where it gradually became evident that it was possible to provide conceptual bridges between various modelling approaches. In 2000, Gustafsson [13] published a paper on Poisson Simulation that filled a gap in the modelling toolset and enabled stochastic compartment modelling based on Time Slicing. Poisson Simulation could then be used as a bridge to ABM and EBM on one hand, and to SBM on another. It also revealed a simple and direct relationship between discrete and continuous compartment models. Gustafsson and Sternad [23] , based on [14] , showed that agent- and entity-based and compartment-based models will produce fully consistent results if a number of simple rules are obeyed. In [24] this was extended to include situation-based models. In [22] , conditions for when the results from a deterministic and continuous model are consistent with those from a stochastic and discrete model were investigated. In particular, the effects of omitting transition, initial value and parameter stochasticities were examined.
The present paper is based on these studies, but goes significantly further to present a common theoretical framework for modelling and simulation of population systems. It can be used as a guide to population modelling for simulation. The intention is also to introduce and use a consistent and unambiguous notation that clearly distinguishes between the population system under study and the model of it, and that can be used in a context that spans all model categories and representations.
One aspect stressed is the development of a conceptual model as an intermediate step on the way towards constructing a simulation model. Also later on in a modelling project, this distinction is important. For example, the validation phase includes validation of hypotheses, which compares the system under study with the conceptual model, and technical validation, which compares the conceptual model with the simulation model.
The ways in which objects with various properties and behaviours can be conceptually modelled as subjects with attributes and procedures are also described. We obtain different representations by placing attributes and/or procedures internally or externally with respect to the subjects. However, irrespective of whether the model is represented as an ABM, EBM, CBM or SBM, the dynamics is obtained by updating the subjects” attributes by procedures internal or external to the subject. This dynamic updating, although differently implemented, has the structural form of interplay between attributes (initiated at time zero) and procedures (possibly affected by external parameters).
The ABM, EBM, CBM and SBM presented in this paper form a consistent framework for stochastic population models. These are the four major techniques for modelling and simulation of population systems. However, there are other, more and less related techniques for creating stochastic and dynamic population models. For example, a Petri net is a hybrid of the model types discussed above that can be included into the presented discrete framework. See Appendix C. For special situations when the spatial aspects are crucial, a cellular automaton model may be an option.
Apart from the holistic approach to modelling and simulation of populations presented here, there are many interesting contributions developing within this field. The applications in physics, chemistry, biology, ecology, epidemics and other areas are too numerous to summarize here. An interesting and modern book about stochastic population processes in time and space is [56] by Eric Renshaw. A recent survey of different approaches to spatial models in epidemiology is [57] . During the last decade, various technical developments of stochastic compartment-based simulation have also been made, for example [58] - [61] .
8. Conclusions
Modelling and simulation to describe and analyse a complex system are based on mathematics, statistics, logic and numerical methods. However, in contrast to these fundamental sciences, modelling and simulation have developed into an unstructured multitude of approaches and ideas that are combined in a variety of ways. This situation exists particularly in the field of modelling populations of interacting objects that evolve over time.
The construction of a population model requires a choice of describing the objects of the population as discrete or continuous, using an agent, entity, compartment or situation-based representation, deciding what types of uncertainties are necessary to handle by alternative structures or stochasticities, formulating adequate output functions, selecting a proper approach for time handling and deciding proper start and termination criteria for the simulations. These choices are usually handled in an unconscious, haphazard or ad hoc way based on modellers’ existing knowledge, which in turn depends on their background, the traditions at their workplace or the type of simulation package at hand, often without considering the requirements and suitability for the problem at hand.
It is important to understand the rules for construction of a population model. In particular, it is crucial to perform the combination of model category, representation, time handling method, implementation of necessary stochasticities etc. in a controlled and clever way without distorting the model. This requires insights about these options, their consequences and the pros and cons of the options. In particular, it is important to know when and how to simplify the model without distorting the results or violating the purpose of the study. A well-performed problem definition and a clever choice of the constituents of a simulation model will drastically reduce the work and increase the probability of a successful population study.
A unified framework of population modelling has been presented here in order to help navigate through this maze, understand the choices available, focus on important issues and highlight the consequences and trade-offs of various choices. The relationships between different representations and how to translate one type of model representation into another have also been treated.
The scope of this paper is restricted to modelling and simulation of population systems. A general theory on model building for simulation would require extensions and perhaps new concepts. For example, simulation may be used to describe the deformation of a single object in three dimensions, the development of the weather etc. based on partial differential equations solved by finite element methods. However, the fundamental constituents such as discrete or continuous description, representation, stochasticities to handle uncertainties, output functions, time handling and termination criterion will still be building blocks for other types of models than population models. It is our hope that the present paper can contribute to the development of a more general theory of modelling for simulation.
Appendix A: Technical Realisations of Transition Stochasticity
The chosen time handling principle will affect the expression of the transition stochasticity in a discrete model. Regardless of whether the system is represented as an agent-, entity-, compartment- or situation-based model, the number of transitions during a time step in Micro Time Slicing is Bernoulli distributed, while in Time Slicing it is Poisson distributed, and for Event Scheduling the time between successive transitions is exponentially distributed. Here follows an example of how transition stochasticity can be implemented in a compartment- based SIR model.
Example 5: Transition stochasticity in a simple SIR model
In the stochastic SIR model (similar to Example 2, shown in Figure 6(b)―but without intervention from an authority) the transition stochasticity handles the transfers, F1 and F2, between the S, I and R stages, where the stages, for simplicity, are represented by single compartments.
With Micro Time Slicing. When advancing time by a very small time step, dt, no or occasionally one transition will happen during the time step. The probability of two or more transitions happening can be neglected if dt is sufficiently small. Then transition stochasticity is realised by Bernoulli statistics. The code for this can be:
If ![]() then
then ![]() else
else ![]()
If ![]() then
then ![]() else
else ![]()
Here U[0,1] is a random number drawn from a uniform (0, 1) distribution. (Note that for dt・F1 and dt・F2 to be integer valued, F1 and F2 have to take the value 1/dt for a transition.)
With Time Slicing. Using a larger time step, Dt, means that several events may happen during a time step. The number of events per time step for a transition then requires Poisson statistics. The code takes the form:
![]()
![]()
Comment: Time Slicing can also be used in agent-based and entity-based models. Then the agents or entities act individually. However, the total number of events taking place during a time step is still Poisson-distributed, but no random number for this total has to be drawn.
With Event Scheduling. Finally, instead of the number of events per time step, transition stochasticity can be implemented by drawing the time of the next event using exponential statistics.
When there are several places in the model where transitions can occur, the parameter l represents the total intensity of events in all transition places. Then a second line of code is required to randomise the transition place at which the event occurred. For the SIR model with l1 = S∙I∙p and l2 = I/T and l = l1 + l2 the code can take the form:
![]()
If ![]() then
then ![]() and
and ![]() else
else ![]() and
and ![]()
(Note that in Event Scheduling there is no time step. Then ![]() and
and ![]() take the values 0 or 1.) ■
take the values 0 or 1.) ■
Appendix B: A Stochastic Compartment-Based Model Using the Poisson Simulation Approach
The Poisson Simulation (PoS) approach was first published by [13] and in the following year by Daniel Gillespie under the name Tau-leap simulation [47] . PoS is a stochastic extension of deterministic Continuous System Simulation (CSS). A main advantage with this approach is that it follows the CSSL standard [62] and can therefore be implemented in any Continuous System Simulation Language provided that a Poisson-distributed random number generator is part of the package or can be included. However, it is also easy to write the code from scratch in any programming language. In a Forrester diagram, a continuous and a discrete (PoS) model can be described as in Figure B1.
As discussed in Section 4.5 and Appendix A, the number of transitions during a short time step Dt, here denoted DT, is (approximately) Poisson distributed.
Considering the stochastic SIR model in Example 5 in Appendix A, using Poisson Simulation it can be coded as shown in Figure B2 (in the very readable language Pascal).
Parameter stochasticity and initial value stochasticity can be included by drawing parameter values (for p and T) and initial values (forS, I and R) from appropriate statistical distributions.
The embedded continuous SIR model is obtained by removing the Po[ ] parts (only keeping the arguments). Then the code:
F1DT := Poisson(DT * p * S * I) takes the form: F1DT := DT * p * S * I and
F2DT := Poisson(DT * I/T) takes the form: F2DT := DT * I/T
This shows how the deterministic, continuous SIR model is embedded in the stochastic model.
Powerful features of the Poisson Simulation approach:
It can be used in almost any CSS language. The only requirement is that a random number generator for Poisson distribution exists or can be included.
It gives clear, compact models that are easy to write, modify and to extend.
Parameter and initial value stochasticities can also be straightforwardly included.
It is efficient to execute.
It is easy to include time functions of all kinds because of the regular time handling.
Statistical output analysis becomes easy because of the regular time handling.
The corresponding continuous model is embedded and easy to extract.
![]()
Figure B1. The transitions between two compartments for continuous and discrete population models. In the latter case the number of transitions can be Poisson distributed.
![]()
Figure B2. Code for the SIR model in Example 5, Appendix A using Poisson Simulation.
Appendix C: Petri Nets
In the classification of discrete simulation models, we saw that there are many possible combinations of representation and time handling. Other types of representations than exemplified in Section 4.2.3 can fit into this classification.
For example, a Petri net is a flexible type of model with many variations and extensions. Here we mainly discuss stochastic Petri nets.
A Petri net uses directed arcs to connect places and transitions in a structure. In this structure, tokens that represent objects can be transferred between places that can hold zero, one or several tokens. Figure C1 shows a simple net containing the basic components of a Petri net.
A Petri net fires when there are a sufficient number of tokens in all input places connected to a transition. Then the transfer between places, P1 and P2, takes place immediately, but it is divided into two sub-steps; from P1 and into the transition, and from the transition into P2 (a transition cannot hold tokens). This division makes it possible to have a number of tokens leaving P1, but another number of tokens arriving at P2. The Petri net can also be expressed in matrix form. For a further description of Petri nets, see e.g. [38] .
Here we connect to the discrete simulation world and see how a stochastic Petri net fits in our classification.
A stochastic Petri net may resemble an entity-based representation in that there are tokens travelling a track of stations (places). However, because the tokens do not have an identity, they are just a number of tokens in a place―so a place has the function of a compartment holding a number of anonymous subjects. There is also a rule (probability) in the stochastic case deciding when a token is to leave the compartment. In fact, this is a compartment-based representation―similar to a stochastic compartment-based model of the kind we have described in this paper. The only particular characteristic when it comes to representation is that the transfer of a token is subdivided into two steps. This can, however, also be accomplished in e.g. continuous system simulation as shown in Figure C2.
A simple Petri net shows only the sequence of events, but timing can be included. In stochastic Petri nets, time handling can be introduced by drawing random numbers from appropriate distributions. Then Micro Time Slicing, Time Slicing or Event Scheduling can be used.
The condition for the number of tokens in a place to fire can also be defined in the “flow equations” of a compartment-based model. Several tokens can also leave or enter batch-wise in such a model.
The SIR model
Figure C3 shows a SIR model, implemented as a Petri net.
![]()
Figure C1. A Petri net consists of places, transitions and arcs from place to transition or from transition to place. The objects of the system under study are represented by tokens (usually without attributes).
![]() (a) (b)
(a) (b)
Figure C2. (a) The Petri net in Figure C1 can often be represented by a simple compartment-based model; (b) If the number leaving P1 is different from the number entering P2, this is prepared for in a Petri net, but it can also be achieved in a stochastic compartment-based model where the transfer takes place in two steps?elimination and creation.
![]()
Figure C3. A SIR model implemented as a Petri net. Note that tokens in both the S and I places are necessary for firing the transition T1. The arc from I back to T1 technically consumes one token from I when firing. Therefore, two tokens from T1 to I are required to compensate for this.
NOTES
![]()
1In e.g. the simulation package Insight Maker [27] [28] , “Spatial geographics” and “Network geographics” are used. In the latter case, attributes can be used to keeptrack of the subject’s network.
![]()
2We can choose to describe all behaviours of an object by one or several procedures. In this paper we often use the singular form.
3We use the word “surroundings” for what is outside the population of subjects in the model (for example resources that can be consumed or temporary allocated or the weather that can affect the behaviours of the subjects), while “environment” is reserved for what is outside the boundaries of the system under study.
![]()
4We use the abbreviations ABM, EBM, CBM and SBM for both models and representations.
![]()
5The situation is usually called “state”, a word we try to avoid in this paper because “state” has different meanings indifferent representations. We can talk about the state of an individual, the state of a compartment and the state of the entire system―but we don’t want to use the word “state” without a specification.
![]()
6Transition stochasticity is often called demographic stochasticity and parameter stochasticity is often called environmental stochasticity in biological and ecological population models, see e.g. [6] [42] .
7This inseparability is important. There are many awkward examples of trying to separate dynamics and stochastics by adding stochastic noise to a deterministic model, which creates a number of artefacts. See e.g. Example 3 in Section 4.1 in [24] .