Received 10 February 2016; accepted 5 April 2016; published 8 April 2016

1. Introduction
Some elaboration is necessary to estimate the effective social discount rate in a dynastic social planning problem because such a rate is unobservable. Many preceding studies rely on Ramsey-type optimal growth theory for the estimation (Ramsey [1] ). Whenever the rate of time preference exceeds the rate of interest, the optimal consumption proportionately decreases because current consumption is more advantageous than the future. Accordingly, the following well-known formula is obtained:
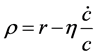 , (1)
, (1)
where ρ is the rate of time preference, and r is the (real) rate of interest. η and  denote the elasticity of marginal (instantaneous) utility1 and the increase rate of consumption, respectively.
denote the elasticity of marginal (instantaneous) utility1 and the increase rate of consumption, respectively.
In discounting the far-distant future events by the Ramsey rule in Equation (1), two approaches are noted (Arrow, et al. [2] ). One is the descriptive approach, which typically focuses on the opportunity cost of capital whose level is observable as the rate of return on alternative investments in the market (Nordhaus [3] ). The advocates of this approach employ the opportunity cost of capital as the discount rate since they claim that investments in reducing climate change must compete with alternative investments in the market2.
The other approach is dubbed the prescriptive approach, where the advocates maintain the view that the market interest rates fail to indicate the trade-offs in consumptions across generations and that the discount rate should be derived from an ethical point of view. These advocates include Cline [4] and Stern [5] . Proponents of both approaches use the same Ramsey rule of Equation (1) in interpreting their discount rates.
Nevertheless, such arguments are erroneous from the rigorous view point of standard economic theory. Even though the utility function is cardinal and measurable in terms of money, there is no theoretical basis for discounting future utilities by the real interest rate. Whenever the real interest rate differs from the rate of time preference, which must be genetically applied to discounting future utilities, a social planner misevaluates the future utilities.
For example, suppose that the real rate of interest exceeds the rate of time preference, and that a social planner applies the real rate of interest to the social discount rate. This implies that the social planner underestimates the future utilities, and hence the undertaken consumption stream is excessively concentrated within the near future compared with the optima path.
In sum, neither approach stands on theoretically firm logic in the sense that they both regard the interest rate as the social discount rate3. What is important in this discussion is that the intertemporal utility should be evaluated by the consumer’s effective rate of time preference, which represents how much future consumption deserves in terms of the current consumption with taking the effect of the interest rate to optimal path into consideration4.
In addition, as we argue later, the existing approaches assume that there is no negative externality postulated in the rule5. According to Equation (1), except for a stationary state, the rate of time preference is lower than the rate of interest as far as consumption grows. Those who infer that the time preference in a social planning might be lower than the market interest rate focus on refining the estimation of the second term of Equation (1) (i.e.,
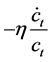 )6.
)6.
However, when one analyzes the efficient allocation of public bads such as the emissions of CO2, one finds that Equation (1) alienates the effect caused by such negative intertemporal externalities. This calls for an extension of the theory.
Suppose that unit current capital investment not merely strengthens the production capacity of an individual firm but also, via the aggravation of global warming, if not offsetting the former positive effect, lowers overall productivity. Let this rate be denoted ψ. In this case, the social rate of return is less than the rate of interest.
This study obtains the following modified formula:
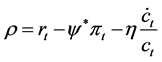 (2)
(2)
where ψ* is the optimal carbon tax rate that is derived in the Section 3, and πt denotes income per capital. Thus, one finds that the optimal carbon tax, which reflects the true productivity of capital, retards the increase of consumption, and hinders excess emissions.
This article is organized as follows. Section 2 reviews theoretical problems, which preceding research commonly holds. Section 3 derives the modified Ramsey rule as in Equation (2) and discusses its implications. Meanwhile, since the modified Ramsey rule is only a portion of an optimal growth theory with a negative intertemporal externality such as the concentration of CO2, stability of the overall economy and equilibrium stationary growth rate are examined by a general equilibrium model. Section 4 considers how emissions-reducing technology affects the welfare of world economy. Section 5 concludes with brief remarks.
2. Critique of the Cost-Benefit Approach
In this section, we briefly review the existing research, and clarify the serious misunderstandings as to which rate should be applied as the social discount rate.
All existing studies of this issue are based on Ramsey-type models. Accordingly, the ultimate objective function is the integral of the discounted (including zero discount rate) instantaneous utility such that
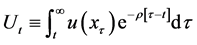 . (3)
. (3)
What one should note is that the correct social discount rate is not the interest rate in the market but the rate of time preference.
Meanwhile, we do not exclude the effect associated with a change in interest rate. Such an effect is, however, indirect in the sense that the interest rate appears only in the budget constraint, not directly in the utility function. As such, the rate of time preference should normatively be equivalent to the social discount rate. Thus, in contrast to Nordhaus [7] , Weitzman [8] and Stern [6] ―which strive to infer the effective interest rate through Equation (1) in order to avail this rate for cost-benefit analysis concerning investments for reducing emissions of CO2, one must concentrate on how to estimate the effective social discount rate by using the observable and measurable economic variables.
As the foregoing discussion illustrates, the preceding studies, which commit themselves theoretically by defining the effective interest rate as the social discount rate, are erroneous in general. We consider whether there is a case in which their cost-benefit approach becomes valid.
Since the interest rate is not related to the individual’s time preference, this rate will affect the economic decision via the intertemporal budget constraint. In terms of the foregoing discussion, as long as the interest rate is the social discount rate, this rate should be equalized with the rate of time preference via a dynamic optimization under some specific instantaneous utility function.
Since the cost-benefit analysis, which applies the rate of interest to the discount rate, assumes that the marginal monetary gain obtained by a project is not affected by the level of the gain in itself, the marginal utility of consumption (or marginal utility of money) should be constant over time. Accordingly, if the interest rate is equalized with the social discount rate, the corresponding instantaneous utility function is
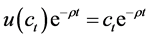 . (4)
. (4)
The Hamiltonian, H, in this case is
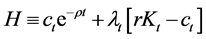 . (5)
. (5)
The optimization conditions are
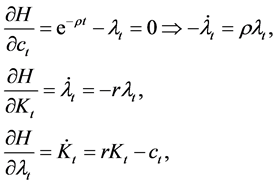 (6)
(6)
where r denotes the interest rate and Kt is the total amount of capital. By the two top equations in (6), we can confirm that the interest rate coincides with the rate of time preference, and thus one can avail the interest rate as the social discount rate instead of the rate of time preference.
Even though the discounting utility by the interest rate is admissible, one must note that the second term of
the right-hand side of Equation (1), 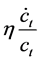 , never appears, because this term corresponds to the effect related to
, never appears, because this term corresponds to the effect related to
the intertemporal substitution effect (consumption smoothing effect) that appears only in the case of decreasing marginal utility; and such a case never emerges in Equation (4).
To summarize, none of the cost-benefit approaches, that apply the market interest rate to the social discount rate, will support the formulation given in Equation (1).
3. Critique of the Cost-Benefit Approach
Section 2 reveals that all preceding analyses contain two logical inconsistencies. One is that although the Ramsey rule in Equation (1) is upheld insomuch as the instantaneous utility function is concave, those cost-benefit analyses using the interest rate as the social discount rate are validated only when the utility function is linear. The other flaw of the preceding approach is that their models do not contain the intertemporal negative externality caused by emissions of CO2. As such, we construct an optimal growth model with a dynamic negative externality assuming a concave instantaneous utility function.
3.1. The Derivation of the Modified Ramsey Rule
Since Equations (1) and (2) are derived from the local maximization obtained on the optimal path, it is sufficient to consider the optimality condition between two sequential periods. Let the global aggregate production function, f, be denoted as7
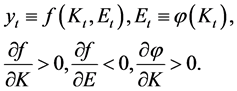 (7)
(7)
yt denotes the volume of current output, Kt, Et are the capital stock and the accumulated emissions of CO2 that prescribe the environmental condition, respectively, and φ is the function that represents the emissions accumulated achieved through the use of capital8.
Consequently, the social planning problem that one must solve is
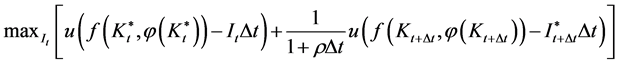 , (8)
, (8)
subject to
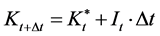 , (9)
, (9)
where u is a strictly concave utility function. 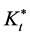 is the optimal capital stock at the beginning of period t that has been determined beforehand by past decisions;
is the optimal capital stock at the beginning of period t that has been determined beforehand by past decisions; ![]() is the given optimal investment during period
is the given optimal investment during period![]() ; and ρ denotes the instantaneous rate of time preference.
; and ρ denotes the instantaneous rate of time preference.
Since the productivity slowdown brought by the CO2 emissions is treated as a negative externality for each firm, the profit-maximization condition requires
![]() (10)
(10)
where r is the instantaneous interest rate. In addition, let us assume that a proportional carbon tax is incurred on the productivity of capital, which aims at internalizing the negative externalities originating from CO2 emissions. We denote the instantaneous tax rate as ψ. The optimal tax rate ψ* is obtained by calculating the marginal negative productivity of capital brought about by the emissions. Thus, one obtains
![]() (11)
(11)
Thus, the optimal instantaneous tax rate ψ* is equal to the product of the elasticity of capital income with respect to accumulated CO2 and the elasticity of emissions with respect to existing capital.
Furthermore, one must note the following relationships:
![]() ,
,![]() . (12)
. (12)
Differentiating Equation (8) with respect to It, and taking the relationships in Equations (10), (11) and (12) into consideration, one obtains
![]() (13)
(13)
Dividing both sides of Equation (13) by Δt, one can ascertain that
![]() (14)
(14)
Taking the limit ![]() of Equation (14), one finally obtains the following representation:
of Equation (14), one finally obtains the following representation:
![]() . (15)
. (15)
For example, if the form of the production function is
![]()
and the utility function belongs to the constant relative risk aversion (CRRA) family, the formula in Equation (15) becomes an exact solution.
3.2. Implications of the Derived Rule
First, we shall consider the economic meaning of the rule in Equation (15). The most prominent feature of the rule is that the social rate of return from unit capital accumulation is lower than the real interest rate r. This is because additional capital reduces productivity via the accumulation of CO2 emissions. This negative effect appears in the second term of the right-hand side of Equation (15). Since ψ* is determined optimally in order that it completely internalizes such a diseconomy, the second term of Equation (15) corresponds to the exact carbon price that has to be paid for the efficient intertemporal resource allocation. Thus, the social rate of return of capital is lowered by ![]() in comparison with the market interest rate. Accordingly, the rate of time prefe-
in comparison with the market interest rate. Accordingly, the rate of time prefe-
rence ρ is strictly smaller than the rate of interest, r, in the stationary state where ![]() holds. Such a constant
holds. Such a constant
consumption path is dubbed sustainable by Dasgupta-Heal [15] and Solow [16] 9. This definition of sustainability seems to be characterized by the faire intergenerational opportunities for consumption, although the analysis is formulated as an optimization problem of representative economic agents with infinite longevity. In Section 3.5, it will be shown that a sustainable economy in the sense of Dasgupta, Heal and Solow is also a zero-growth economy to the extent that there is no technological progress in CO2 reduction, as will be discussed in Section 4.
3.3. The Effective Social Discount Rate: Is Discounting a Vice?
In this subsection, an effective social discount rate under the modified Ramsey rule given by Equation (15) is derived. For simplicity, it is assumed that the instantaneous utility function belongs to the constant relative risk aversion (CRRA) family, the marginal utility elasticity of which is denoted η. The effective social discount rate, ρE, is defined as the rate by which the discounted future utility is equalized with the discounted value of current utility. That is,
![]() . (16)
. (16)
Equation (16) can be transformed into
![]() (17)
(17)
Dividing both sides of the equation by Δt, rearranging the terms, and taking the limit![]() , an elementary calculation and the modified Ramsey rule lead us to
, an elementary calculation and the modified Ramsey rule lead us to
![]() . (18)
. (18)
Equation (18) has a prominent feature. The optimal carbon tax, which is levied on capital income, raises the effective social discount rate. Neither supporters of the descriptive nor the prescriptive (ethical) approach find such a paradoxical result. Supporters of the descriptive approach are apt to regard the optimal interest rate as higher than it is in actuality. This is because they might be inclined to consider that the climate change is not serious enough in general and that people should demand a high social discount rate, which is applied to the emissions-saving investment.
The ethical approach emphasizes the converse consequence. However, the perspective that a high interest rate means a high social discount rate is commonly shared despite of the profound rift between the policy recommendations of the two approaches.
The seemingly counterintuitive fact that a high interest rate corresponds to a lower effective social discount rate has firm roots in the correct interpretation of Ramsey rule in Equation (15). Equation (15) does not determine the interest rate, but describes the dynamic path of consumption. If the rate of time preference is larger than the interest rate, people enjoy much greater current consumption than future, and vice versa. Accordingly, a higher interest rate prompts a longer time horizon and preference toward future consumption; thus, the corresponding effective discount rate becomes lower as is apparent in Equation (18).
In other words, the carbon tax provides the true rate of return for capital and lowers the effective interest rate. This allows a high social discount rate, which enables to the reduction of consumption and capital investment over time. It is natural that values of these macroeconomic variables should be reduced whenever the world economy is caught in the situation in which excess consumption and investment causes excess concentration of greenhouse gases. To summarize, it is quite a natural consequence that the social discount rate moves in the opposite direction to the rate of interest.
Finally, one must note that, in contrast with an overlapping-generations model, a higher social discount rate does not mean the exploitation of future resources in a dynasty model. Accordingly, no ethical problem is provoked by applying a high social discount rate.
It should be emphasized that the Ramsey rule, while important, in general, is only one component of an optimal growth theory. The dynamics of emissions and/or accumulation processes of capital should be simultaneously analyzed. That is, one needs a full model of optimal growth that contains the negative and intertemporal external economy caused by CO2 emissions. This is the topic we shall analyze in subsequent subsections.
3.4. Modifying the Ramsey Rule to Analyze the Global Warming Problem
The Ramsey rule ![]() is a special case of our formula (2) which corresponds to the case where
is a special case of our formula (2) which corresponds to the case where ![]()
and r = const. One should note that since the production function of each industry is linear against capital, the aggregation is feasible. Thus, we obtain the macroeconomic production function F as
![]() (19)
(19)
Equation (19) implies that no scarce production resource other than capital exists. This fact demonstrates that there is a serious drawback in the use of the standard Ramsey model to analyze the global warming problem.
This is because the scarcity that originates from the quality of our atmosphere (measured by the mass of CO2 it contains), is the vital issue in this problem. As such, unless we assume some optimistic exogenous emissions- absorbing technological progress, as will be analyzed in Section 4, it is a plausible theoretical formulation that the aggregated production function suffers from diminishing returns to scale owing to the Marshallian negative externality originating from CO2 emissions. That is, theoretically, the congestion that emerges from polluting the atmosphere intensively is the very core global warming problem.
3.5. The Limit of Economic Growth: The Case of a Linear Homogenous Individual Production Function with Marshallian Diseconomy
We heretofore assume that the instantaneous rate of interest, r, is constant over time. However, as Equation (10) shows, this varies together with capital accumulation. Let us assume that
![]() . (20)
. (20)
This assumption implies that the marginal product of capital of individual firms is constant or decreasing and that the marginal external diseconomy increases with capital accumulation. Accordingly, the relationship between capital stock, K, and the instantaneous social rate of interest, r, becomes the downward sloping curve illustrated in Figure 1. This method is a simple application of endogenous growth theory, which originates from Romer [18] .
The feasibility condition of the economy is depicted as
![]() . (21)
. (21)
Equations (15) and (21) describe the law of motion of this economy. Average productivity of capital, πt, is a decreasing function of capital, Kt10, and the inside of the bracket of the right-hand side of Equation (21) is positive. If these effects dominate the effect of decreasing marginal product of capital, the locus of (c, K), which satisfies![]() , becomes upward-sloping as Curve KK illustrated in Figure 2.
, becomes upward-sloping as Curve KK illustrated in Figure 2.
On the other hand, the locus of (c, K) that satisfies ![]() is obtained by Equation (11). To the extent that the effective interest rate,
is obtained by Equation (11). To the extent that the effective interest rate, ![]() , is a monotonously decreasing function of capital, K, by Equation (15), some K*
, is a monotonously decreasing function of capital, K, by Equation (15), some K*
![]()
Figure 1. Marginal productivity of capital.
exists that satisfies![]() ; thus the locus of
; thus the locus of ![]() becomes horizontal as illustrated by curve CC in Figure 2.
becomes horizontal as illustrated by curve CC in Figure 2.
It is clear from Figure 2 that if the world interest rate is located above curve KK, capital accumulation advances. Otherwise, disinvestment should be hastened by the carbon tax because too many emissions have already accumulated in such a situation. Ultimately, the world economy converges to Point E. This demonstrates that there is a limit to the world economy’s growth; and this converges to zero economic growth when a significant negative intertemporal externality such as global warming exists.
In addition, one can ascertain that other paths such as AA or BB are not optimal as follows. Let us consider path AA. On path AA, people initially experience excess consumption compared with the optimal path. Such inertia does not cease even when the level of capital falls below the critical level K*, because a shortage of capital lowers the effective social discount rate (raises the effective interest rate) as discussed in Section 2.3. Accordingly, capital depletion advances. The economy eventually reaches a bankruptcy point such as EB and no consumption is possible thereafter. Since the principle of optimality proposed by Bellman requires that an initial optimal policy should be also optimal with respect to subsequent periods, and since stationary state EB is Pareto inferior to Point E, it is evident that path AA is not optimal.
Path BB is also non-optimal. This path is characterized by excess capital accumulation and shortage of consumption. Even when the economy crosses curve KK, where investment temporarily ceases, the decrease in consumption does not stop because the effective social discount rate is high enough (the interest rate is low enough). Accordingly incessant capital accumulation occurs and the consumption level asymptotically approaches zero. Accordingly, again from the principle of optimality, such a path is not optimal.
What one must note is that even though the production function of each economy is a linear function on capital stock, which means that
![]() , (22)
, (22)
Equation (14) still holds, and thus the properties of Figure 2 are preserved. This means that our atmosphere is not a renewable resource for human beings overall, and therefore, even though the anthropogenic technological system in the short run contains no non-renewable resources, the gradation of the quality of atmosphere creates a bottleneck in the production/consumption process in the long run. It is apparent that a constant growth path of consumption levels is unfeasible as long as the aggregate production exhibits decreasing returns to scale and the interest rate is endogenously determined.
4. The Rule ![]() and Technological Progress
and Technological Progress
Preserving the relevance of the rule ![]() in the context of the global warming problem, we need to
in the context of the global warming problem, we need to
introduce some exogenous technological progress that reduces the concentration of CO2 at a constant rate β. In such a case, for example, the production function of firm ω becomes
![]() . (23)
. (23)
The inside of the bracket indicates the external effect associated with the concentration/reduction of CO2, which corresponds to the exogenous total factor productivity (TFP) for each firm. Accordingly, as long as the TFP is kept constant, the world economy can achieve a steady growth rate because the macroeconomic production function becomes linear.
By Equation (23) such a rate is represented as
![]() , (24)
, (24)
![]() (25)
(25)
Applying Equations (24) and (25) to formula (2) at the stationary state, one obtains
![]() . (26)
. (26)
In addition, from the budget constraint,
![]() (27)
(27)
holds. Thus, Equation (26) at the steady state equilibrium becomes
![]() . (28)
. (28)
In other words, Equation (28) implies that the feasibility of future increases in consumption relies entirely on autonomous technological progress in the reduction of the stock of CO2.
The stability of the stationary state can be proved as follows: Since
![]() , (29)
, (29)
logarithmically differentiating Equation (29) with respect to time, one obtains
![]() . (30)
. (30)
where![]() . Again, from the budget constraint and the optimality condition (15), one obtains
. Again, from the budget constraint and the optimality condition (15), one obtains
![]() (31)
(31)
When linear approximation around the stationary state is applied to the right-hand side of Equation (31), one can ascertain that
![]() . (32)
. (32)
Thus, our economy can be described by two differential equations on ![]() as expressed in Equations (30) and (32). There is ambiguity in the sign of the second term of (32). This is because growth rate is affected by two opposite factors from the interest rate. One factor is that a high interest lowers the social discount rate and stimulates consumption. This effect retards capital accumulation. The other dynamic is rather indirect; the heightened interest rate raises real income and accelerates capital accumulation as a residue of real income minus consumption. Let the latter effect be assumed to dominate the former, as assumed in Section 3.5. Then, the second term of the right-hand side of Equation (32) becomes negative.
as expressed in Equations (30) and (32). There is ambiguity in the sign of the second term of (32). This is because growth rate is affected by two opposite factors from the interest rate. One factor is that a high interest lowers the social discount rate and stimulates consumption. This effect retards capital accumulation. The other dynamic is rather indirect; the heightened interest rate raises real income and accelerates capital accumulation as a residue of real income minus consumption. Let the latter effect be assumed to dominate the former, as assumed in Section 3.5. Then, the second term of the right-hand side of Equation (32) becomes negative.
The phase diagram of this system is illustrated in Figure 3. Accordingly, the economy has a saddle-point property, and the planned economy can achieve these stable paths, which converge to the stationary equilibrium, E. Thus, equilibrium growth rate of consumption in the steady state is equal to β, and the rule (28) is upheld.
![]()
Figure 3. The phase diagram: the case of technological progress.
5. Concluding Remarks
A modified Ramsey rule with a negative intertemporal externality (e.g., caused by the excess emissions of CO2) has been developed. According to the rule, a proportional carbon tax rate to income per capital is required to achieve the efficient intertemporal allocation of emissions of CO2. Even under a sustainable equilibrium where the aggregate consumption level is kept constant, such taxation is unavoidable because of the dis-incentivizing further emissions. It is notable that such a negative effect is not taken into consideration in the preceding articles analyzing the global warming problem despite of its importance.
Second, the optimal rate of the proportional carbon tax is derived explicitly. The rate is equal to the product of the elasticities of output to emissions and emissions to capital. That is, the optimal carbon tax rate per unit capital income is equal to how many outputs are curtailed by an increase in capital by one percent owing to the negative externality caused by emissions.
In addition, one should note that a higher interest rate implies a lower discount rate in optimal growth theory. The causality, which the Ramsey rule asserts, is that consumption increases with the difference between the interest rate and the rate of time preference. Accordingly, consumption increases with the interest rate over time because individuals find more advantage in postponing consumption. This implies that the social discount rate is lowered by an increase in the interest rate; thus, a higher interest rate aggravates the global warming problem. Both descriptive and prescriptive (ethical) approaches, which are noted in Arrow et al. (1996), are prone to overlook this relationship. In reality, applying a proportional carbon tax is the proper diagnosis for mitigating the global warming problem. This is because a higher social discount rate suppresses future consumption, or equivalently, future CO2 emissions.
Finally, it is proved that, to the extent that there is no technological progress which lessens the stock of CO2 in the atmosphere and overall emissions control assures the viability of human beings, there is a limit of economic growth and the world economy will reach a zero-growth era eventually. This is because a quality atmosphere is a scarce and unreproducible resource of production; thus, the aggregate production function comes to exhibit decreasing to scale.
NOTES
1Three kinds of interpretation of the elasticity of marginal utility are known (Stern [6] ). They are intratemporal distribution, intertemporal distribution and attitudes to risk, respectively. Directly related to our argument is the intertemporal distribution and we postulate that we can set the appropriate values for η.
2See also Nordhaus [7] and Weitzman [8] .
3In addition, the formula in Equation (1) does not provide the solutions for the rates of time preference ρ or elasticity of marginal consumption η endogenously, leaving each advocate to assign appropriate values as parameters according to one’s observations or value judgement.
4A serious misunderstanding exists concerning the role of rate of time preference and interest rate in existing approaches. An increase in the interest rate implies a lower (not higher) social discount rate because future consumption becomes more advantageous. That is, one should note that the social discount rate must be high enough if one wishes suppressing excess consumption/emissions. We will intensively discuss this property in Section 3.3.
Introduction of uncertainty into discounting leads us to a theory of declining discount rates (Arrow, et al., [9] ). For example, uncertainty in the growth rates of future consumption (see Gollier [10] ) and uncertainty of future discount rates such as the rates of return on investment (see Weitzman [11] and Gollier-Weitzman [12] ) will typically cause the discount rates to decline as time goes by.
5See Section 3 to find the limitations of the standard Ramsey rule. See also Section 4 for the scope of its validity in relation to technological change. Examples of other approaches where the social discount rate is endogenously derived are found in Otaki [13] [14] .
6Such an assertion made mainly by advocates of the prescriptive approach is unacceptable from the view of economic growth theory. A large increase rate, 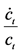 , is not a cause but a consequence of a low rate of time preference ρ. This fact implies that a low rate of time preference corresponds to a low social discount rate. However, a low social discount rate evaluates future consumption more highly; thus, this delays the mitigation of CO2 emissions.
, is not a cause but a consequence of a low rate of time preference ρ. This fact implies that a low rate of time preference corresponds to a low social discount rate. However, a low social discount rate evaluates future consumption more highly; thus, this delays the mitigation of CO2 emissions.
7We assume that each economy in the world has the same production and utility function, as well as the same endowments. Accordingly, such functions can be aggregated.
8We do not exclude the possibility that an economy-wide carbon neutral technology that effectively absorbs emitted CO2 might become available; and/or that non-carbon-emitting energy resources are fully used in order to avoid the increase of CO2 concentrations. For more detail, see Section 4.
![]()
9Note that Solow [17] is skeptical about the arbitrariness of the concept of sustainability.
10Since ![]() holds.
holds.