Single Track Laser Surface Hardening Model for AISI 4340 Steel Using the Finite Element Method ()
Received 20 February 2016; accepted 5 April 2016; published 8 April 2016

1. Introduction
Laser hardening is a surface transformation process capable of heating the desired mechanical part quickly and locally. This innovative and advanced technique has many advantages compared to other surface heat treatment processes such as flame or induction heating. In fact, it is known for its high degree of controllability and automation, low part distortion, and selective and precise treatment. When the part is locally heated and quenched rapidly, a martensitic layer is created that offers some fatigue and wear resistances compared to the unaffected base material [1] [2] .
Several investigations have been done in the field of heat treatment of steel by laser to evaluate the sensibility of steel hardness profiles for a variety of laser parameters. The trial and error method is principally used to establish the contribution of different laser parameters to the dimensions and microstructure of the hardened depth. Considerable research studies (Shin et al. [3] , Dinesh et al. [4] , Qiu et al. [5] , and Shiue and Chen [6] ) have been carried out to examine the influence of single track laser hating process parameters on the characteristics of hardening, such as the hardness and dimensions of the hardened zone, with a microstructural comparative study of different zones of the workpiece. These process parameters include the power of the laser, the travel speed, the focal position, and the composition of the steel. Authors (Qiu and Kujanpaa [7] , and Santhanakrishnan and Kovacevic [8] ) focused on linear oscillation scanning with a laser, and its effect on steel surface hardness uniformity.
Numerical modeling of laser heat treatment is an efficient tool for understanding and optimizing the contribution of the process parameters to the final surface hardness of the workpiece. A solution of the Klein-Gordon equation with a Fourier series expansion was used by Leung et al. [9] , to model the moving interface of heat transfer in a laser transformation hardening process of a rectangular AISI 1050 steel workpiece. Shiue and Chen [6] used a simple mathematical calculation based on Ashby and Easterling [10] equation of temperature prediction, to estimate the carbon diffusion distance in austenite during laser surface treatments of AISI 4340 steel.
So and Ki [11] evaluated the effect of specimen thickness on heat treatability in laser transformation hardening of AISI 1020 steel. This study was done using a one-dimensional finite volume solution of the heat conduction equation, to evaluate the capacity for self-quenching in plates according to their thickness. The results were validated with laser heat treatment experiments on AISI 1020 steel specimens. In another work, Ki et al. [12] evaluated the effect of different type of heat sink in the laser transformation hardening of carbon steel sheets. The thermal conductivity of the heat sink and the thermal contact resistance between the steel sheet and the heat sink were identified as the two primary parameters for the process. The same one-dimensional heat conduction model was used to simulate the heat-tractability of steel sheets with 2 mm of thickness using four types of heat sink: stainless steel, steel, copper, and no heat sink.
Finite element modeling (FEM) is one of the computation methods available for understanding the behavior of the process and the effect of process parameters on the hardness profile. This method is very effective because of its ability to predict the physical quantities in the investigated part. In the case of laser heating, the temperature distribution is very important to predict the workpiece hardness profile.
Sun et al. [13] used a three dimensional finite element model to calculate the temperature history for laser surface hardening of 42CrMo cast steel. Two shapes of laser beam were used in the hardening of the steel to obtain the required hardened layer. One was a stripy spot with uniform intensity array spots, and the other a stripy spot with intensity blow-up in the edge of the whole array spots. As a comparison, a Gaussian laser beam was also adopted. Another study of three-beam laser heating of a moving steel sheet, using the finite element solution of the heat transfer equation, was done by Shuja and Yilbas [14] without any experimental validation. Temperature and stress fields were predicted and the influence of laser intensity at each irradiated spot on temperature and stress fields was examined.
Li et al. [15] worked on a comparative study between the two types of hardening laser: diode laser and CO2 laser. This study was done for AISI-1045 steel and the effects of various parameters, such as laser power and the speed of treatment, on the structure, case depth and micro hardness were examined. Finite element modeling of the process was developed using constant thermal parameters of the steel to determine the temperature field of the workpiece and to better understand the difference in laser hardening results with these two types of laser. Wu et al. [16] developed a three dimensional numerical model for pulsed laser transformation hardening using the finite element method to solve the heat transfer equation representing the process. The influence of the laser temporal pulse shape on the connection of hardened zone, the maximum surface temperature of the material, and the hardened depth is numerically investigated at different pulse energy levels. The predicted hardening depth for 12J of pulse energy for a duration of 24 ms compared favorably with the experimental trial.
A numerical two-dimensional kinetic model coupled to the three-dimensional thermal model was developed by Skvarenina and Shin [17] , to predict the hardening that occurs in AISI 1536 steel parts during laser heating. The absorptivity and the emissivity of the workpieces were determined experimentally and the values chosen were 0.67 and 0.90, respectively. The models were validated for 1100 - 1220 W laser power and 2.9 - 3.0 mm/s scanning speed. Patwa and Shin [18] used a similar thermo-kinetic model for laser transformation-hardening of AISI 5150H steel, for a cylindrical workpiece. The absorptivity value chosen for the steel was 0.5, and the model validation was done for 400 - 500 W laser power, 6 - 8 RPM speed and 10 - 13.4 mm/s scanning speed.
According to the literature review, the finite element models developed by researchers used constant thermal parameters for modeling the laser heat treatment process. Accordingly most of them are not validated for wide variation in process parameters, such as the laser power and the travel speed of the beam radiation. In this paper, finite element modeling of laser heat treatment on an AISI 4340 steel plate is presented. The model was developed using COMSOL MULTIPHYSICS software to solve the heat transfer equation in the workpiece. Temperature dependant parameters of AISI 4340 steel and a linear interpolation approximation of absorptivity versus temperature were used in the simulation. The experimental tests of the plate laser heat treatment were done with a fool matrix for two parameters with three levels: laser power (400 - 1200 W) and end irradiation scanning speed (10 - 30 mm/s). The center and corners of the matrix tests were used for calibration of the absorptivity function, and the other tests were used for the validation of the model.
2. The Simulation Model
2.1. Formulation
First, confirm that you have the correct template for your paper size. This template has been tailored for output on the custom paper size (21 cm * 28.5 cm).
Laser hardening depends mainly on the temperature variation during heating. Moreover, the microstructure obtained upon cooling is determined according to the maximum holding and cooling rate temperatures. The temperature profile is calculated by Fourier’s classical law of heat conductionto describe the laser surface treatment regarding the thermal quantities and the thermal properties of the steel used, as in (1) [19]
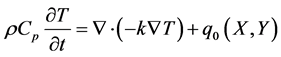 . (1)
. (1)
This equation is used to determine the temperature (T) as a function of the density ( ) the specific heat (
) the specific heat ( ), the thermal conductivity (k), and the heat source (
), the thermal conductivity (k), and the heat source (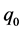 ) modeling the laser irradiation heating.
) modeling the laser irradiation heating.
The thermal interaction between the light and the workpiece is caused by absorption, which determines the heat flux of the irradiated beam absorbed by the part. The absorption depth of the laser irradiation is on the order of its wavelength [20] . In the present study, the wavelength of the ND:YAG laser used is 1.06 μm, so that the laser pulse can be considered as a plane heat source, which is represented by a circular beam shape with a Gaussian distribution of heat flux (Equation (2)) [15] .
 . (2)
. (2)
The surface density of the generated heat (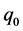 ) depends on the laser power (P), the absorptivity (
) depends on the laser power (P), the absorptivity (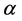 ), the beam radius (
), the beam radius (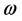 ), and the coordinates of the laser projection source for the part (X, Y), which are calculated by the following equations system.
), and the coordinates of the laser projection source for the part (X, Y), which are calculated by the following equations system.
 . (3)
. (3)
X and Y represent the spatial coordinates of the part relative to the reference point, 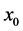 and
and 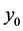 are the initial coordinates of the laser beam irradiation,
are the initial coordinates of the laser beam irradiation,  is the scanning speed of the beam, and t is the heating time. Laser beam movement is measured according to the x axis during heating.
is the scanning speed of the beam, and t is the heating time. Laser beam movement is measured according to the x axis during heating.
It has been pointed out [2] that the heat losses due to convection and radiation can be neglected during laser heat treatment, so the heat source q0 is the only heating source used for the simulation.
2.2. Material Properties
The workpiece modeled in this paper is composed of AISI 4340 steel base material; its chemical composition in weight percent was 0.39 C, 1.68 Ni, 0.64 Cr, 0.15 Mo, 0.67 Mn, 0.22 Si, 0.017 P, and 0.014 S, as given by the manufacturer. The thermal conductivity, specific heat and transformation temperatures are required to model the laser heat treatment of AISI 4340 steel. Martensite transformation temperatures of AISI 4340 steel are Ac1 = 996 K and Ac2 = 1053 K, and the malting temperature is Mp = 1774 K [6] . The temperature dependence of thermal conductivity is based on data gathered from the ASM Handbook [21] , and the specific heat was obtained from the U.S. Department of Defence Military Handbook [22] , as shown in Figure 1. The material density of the workpiece chosen was the same as that predefined by COMSOL MULTIPHYSICS software for AISI 4340 steel (ρ = 7.85 g・cm−3).
The laser-steel interaction is represented by the workpiece surface absorptivity which depends on the wavelength of the laser source, the physical properties of the material, the surface finish, and the processing environment. Throughout the literature many values of absorptivity have been chosen for studying the laser heat treatment: 0.67 [17] ; 0.5 [18] ; 0.8 [2] ; 0.7 [10] ; 0.65 - 0.75 [23] ; 0.7 [24] . The absorptivity value has been a subject of debate for a long time [25] and the large variations in its value can be attributed to its high sensitivity to a particular setup.
In the case of this work, the parts used are of the same type (AISI 4340) and the same surface finish, and the environment is considered stationary during the heat treatment, thus the absorptivity depends primarily on the temperature of the workpiece during treatment. So a linear interpolation approximation between the absorptivity and the temperature was used, and parameters of this function were found and calibrated experimentally later in the study.
2.3. Workpiece Shape and Meshing
The workpiece shape used in simulation is a 15 mm × 20 mm × 4 mm plate (Figure 2). The experiments included single passes of the laser beam on the specimen surfaces, so a refined mesh is used in the zone where the piece is touched by the laser irradiation; the rest of the workpiece is not hardened by the process and works as a heat sink to ensure the self-cooling of the piece, hence a coarse mesh was used in it.
A convergence study was done to determine the best mesh size to choose. In fact, an overly refined mesh gives better results in terms of accuracy, but a long simulation time is needed; on the other hand a coarse mesh allows a faster simulation and less accurate results. This study selects the mesh size yielding the best compromise between the simulation time and the accuracy of results.
The convergence study was conducted for a power of 800 W and a speed of 20 mm/s. The mesh size was varied between 1 mm and 0.2 mm with a step of 0.1 mm. Figure 3 shows the variation of the maximum temperature predicted by the different simulations between two successive mesh sizes for various depths (from the workpiece surface to a depth of 750 µm with a step size of 250 µm).
![]()
Figure 1. Thermal conductivity and specific heat as a function of temperature of AISI 4340 steel.
![]()
Figure 2. Representation of the workpiece with its mesh in COMSOL MULTIPHYSICS software.
![]()
Figure 3. Thermal conductivity and specific heat as a function of temperature of AISI 4340 steel.
A convergence study was done to determine the best mesh size to choose. In fact, an overly refined mesh gives better results in terms of accuracy, but a long simulation time is needed; on the other hand a coarse mesh allows a faster simulation and less accurate results. This study selects the mesh size yielding the best compromise between the simulation time and the accuracy. The convergence study was conducted for a power of 800 W and a speed of 20 mm/s. The mesh size was varied between 1 mm and 0.2 mm with a step of 0.1 mm. For all the mesh sizes the model was trained to evaluate the temperature versus time in different depths, the maximum temperature was recorded in every depth of each mesh size, and compared to the maximum temperature of the next one, more details about the maximum simulated temperature are in section 4 (Model calibration). Figure 3 shows the variation of the maximum temperature predicted by the different simulations between two successive mesh sizes for various depths (from the workpiece surface to a depth of 750 µm with a step size of 250 µm).
The convergence study graph (Figure 3) shows that the 0.7 mm mesh is the coarser mesh size that gives a tolerable simulation error. Thus this is chosen as the optimal mesh size.
3. The Experimentation
3.1. Experimental Set-Up
The study of the laser transformation hardening process consisted of three stages: a pre-heat treatment stage, where the coupon was prepared for the study; a heat treatment stage, where the coupon was subjected to the heat treatment; and a post-heating treatment stage, where the hardened zone dimensions and hardness measurements were determined.
The laser heat sourceconsist of a commercial ND:YAG laser system capable to produce a power output up to 3 kW at 1.06 μm wavelength. An articulated robot enabled moving and positioning the laser’s irradiation and heat treating samples at the scanning speed desired.
The base material used is AISI 4340 steel, cut into plates of 4 mm thickness, 20 mm length and 15 mm width (Figure 4), the samples were oil quenched after full austenitization in the oven, and tempered to blacken their surface and improve laser irradiation absorptivity.
The experiments included single passes of the laser beam on the specimen surface with no overlapping. After the laser transformation hardening, the specimens were cut perpendicularly to the scanning direction and the required surface of each specimen was ground and polished with various grades of emery sheets. The depth of the heat affected zone is determined by the surface hardness profile. Hardness measurements were obtained in the center of the laser track, as outlined in Figure 5 by the dashed line, using Vickers’s tests with a load of 300 g applied for 15 s. For each trial, different hardness profiles with 50 μm steps were measured. The specimens were finally etched with a 5% Nital (5% nitric acid and 95% ethanol) solution and prepared for hardened depth and width measurement by the profile projector.
3.2. Experimental Measurement
The experiments were carried out using a fool matrix for two parameters with three levels: laser power (400 - 1200 W), and irradiation scanning speed (10 - 30 mm/s), all tests are presented in Table 1. The hardness profile measurements for the T1, T5, and T9 tests are presented as examples in Figure 6. The curves are principally composed for three zones: the first one is the closest to the workpiece surface, and represents the melted depth of the heat affected zone; the second one is the zone of maximum hardness and represents the hardened depth of the heat affected zone; the last one is the non-affected zone.
The measurement of the hardened depth and width is done using a profile projector after the chemical attack of the samples with Nital solution. The hardened and the melted depths, determined using the micro hardness machine and profile projector measurements of the samples, are presented in Table 2. The relative error between the hardened depth measurements using the profile projector and micro hardness methods is calculated, and it is noted here that the precision of the measurement using the profile projector is 1 μm and the step of
![]()
Figure 5. The cross section of the workpiece where HW, HD and MD are, respectively, the hardened depth, the hardened width and the melted depth.
![]()
Figure 6. The hardness profile in HRC as a function of depth in µm, for tests T1, T5, and T9.
![]()
Table 1. Experimental tests matrix.
![]()
Table 2. The micro hardness and the profile projector measurements of the heat affected zone.
measurement using the micro hardness profile is 50 μm. The error is estimated using the difference between profile projector and micro hardness measurements. The hardness measurement was done only for the determination of the melted zone during the laser heat treatment.
4. The Model Calibration
4.1. Determination of the Hardened and Melted Zones
After the simulation ran, the temperature profile was used to determine the hardened depth and width and the melted depth. In this study, a cross section of the workpiece is chosen (YZ plane in Figure 2) to determine the hardened zones and the melted zones dimensions. Two groups of points are used to measure temperature history (using MATLAB combined with COMSOL MULTIPHYSICS). The first group represents the temperature evolution in the workpiece surface (Y direction), and the second one represents the temperature evolution in the depth of the workpiece (Z direction). The first group allows the determination of the hardened width, and the second one allows the determination of the hardened and the melted depths. After running the simulation, the temperature history is saved at every point in the two groups, as shown in Figure 7, and the maximum temperature in
![]()
Figure 7. Temperature history versus time for the T5 test simulation at different depths from the workpiece surface.
each one is used to determine the hardened and the melted zones. Paper [26] presents a similar method for the characterization of the hardness profile of AISI 4340 steel in induction heating.
Figure 8 shows the maximum temperature simulated as a function of depth and width for the first and the second groups of points for the test T5, the martensite transformation temperature, Ac3, of the AISI 4340 steel is used to determine the hardened depth and half of the hardened width, and the melting temperature of the steel is used to determine the melted depth.
4.2. Calibration of the Finite Element Model
As mentioned above, a linear interpolation approximation of absorptivity as a function of temperature is used for the absorptivity coefficient. Three points are used to determine and calibrate this approximation: the martensite transformation temperature (A1), the melting temperature (A2), and the ebullition temperature, which is on the order of 3100 K (A3). The absorptivity at the ambient temperature is supposed to be equal to A1. These three temperatures are chosen for the calibration because they represent the different transformations of the steel.
Because of the complexity and the time consumption of the calibration when using three values, the absorptivity at the ebullition temperature, A3, is fixed at 0.1, and the absorptivities A1 and A2 are used in the calibration using five experimental test results: T1, T3, T5, T7, and T9. The other test results are used to validate the model. Several simulations using various values of A1 and A2 were done, and the hardened and melted dimensions of the hardened zone were determined using the temperature history. The results obtained were compared to the experimental results to determine the average error. Figure 9 shows the average error as a function of A1 and A2, and the minimum error is 9.7 % and corresponds to A1 = 0.73 and A2 = 0.57.
5. The Model Validation
To consider laser heating of the steel sheet, temperature fields developed in the heated region are predicted numerically using finite element code. The influence of the location of laser beam intensity and scanning speed on temperature is examined. Since the heating generation is symmetric along the symmetry plane, the results obtained for temperature and stress variations are presented for half of the domain of the irradiated workpiece. Figure 10 shows the temperature contours of T2 and T8 validation tests. Table 3 presents the hardened depths and widths and the melted depths for all calibration and validation test simulations. The average error of validation tests is 7.65%, and the average error of all measurements is 8.83%.
The regression curves between the experimental measurements and the simulation results are presented in Figure 11. The squared regressions between the simulation and the experimental results are 0.98 for the hardened depth, 0.96 for the hardened width, and 0.97 for the melted depth, and therefore the finite element model can predict the heat affected zone dimensions with a good accuracy.
6. Conclusion
In this paper, a comprehensive approach used to build a simplified model for predicting the hardness profile for AISI 4340 in laser surface hardening is presented. Numerical simulation using heat transfer equations, laser irradiation absorptivity approximation and temperature dependent thermal properties of AISI 4340 steel based on
![]()
Figure 8. Maximum temperature in Kelvin versus depth and width in mm for the Y and (Ty) Z direction (Tz) group of points for the test T5 simulation.
![]()
Figure 9. Average error as a function of A1 (X axe) and A2 (Y axe).
![]()
Table 3. Simulated dimensions results of the heat affected zone for all tests.
![]()
Figure 10. Temperature contours in the half domain of the workpiece for the tests T8 (left), and T2 (right).
![]()
![]()
![]()
Figure 11. The regression curves between the experiment measurementsand the simulation results in µm for all tests for the hardened depth (HD), the hardened width (HW), and the melted depth (MD).
COMSOL MULTIPHYSICS software in order to predict the temperature distribution and the hardness profile is discussed. A commercial 3 kW Nd:Yag laser system, a structured L9 experimental design and confirmed statistical analysis tools are used to conduct the experimental study for the prediction model calibration and validation. Five tests are used for the calibration of the interpolated absorptivity function and four tests for the model validation. The results reveal that the numerical simulation can effectively lead to a consistent and accurate model and provide an appropriate prediction of the hardness profile attributes under variable hardening parameters and conditions. With an average error less than 10 % and more than 95% as correlation coefficient, the validation process shows great concordance between predicted and experimental results.