Received 20 January 2016; accepted 22 March 2016; published 25 March 2016

1. Introduction
Profound conceptual incompatibilities exist between General Relativity (GR) and quantum mechanics (QM) as currently formulated. For instance; 1) whereas in GR, time is just another covariantly transforming coordinate of an arbitrarily differentiable spacetime manifold, in QM it is an external, Newtonian parameter and properties are discrete, and 2) the respective macroscopic and microscopic domains of applicability remain as disconnected as ever. The paper proposes perspective at 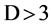 as a possible means of unification. A simple mathematical principle is then invoked as a natural limit on
as a possible means of unification. A simple mathematical principle is then invoked as a natural limit on 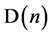 and the implied existence of a “maximum physical reality” therefore means that effects that are clearly perspectival at
and the implied existence of a “maximum physical reality” therefore means that effects that are clearly perspectival at 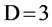 must become “more real” (effectively observer-independent) with each
must become “more real” (effectively observer-independent) with each 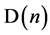 increment. (The apparently microscopic thus becomes the effectively microscopic, and 3-space scale extremes are juxtaposed.) Characteristics of the relationship between the earth- bound observer and the horizon are applied to
increment. (The apparently microscopic thus becomes the effectively microscopic, and 3-space scale extremes are juxtaposed.) Characteristics of the relationship between the earth- bound observer and the horizon are applied to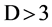 , suggesting perspectival interpretations of space, universal expansion, radiation, entanglement, gravitation, mass, dimensional reduction and measurement (as projection rather than amplification). The difference between apparent flatness of the 2-surface and actual global closure corresponds to the boson of the gauge interpretation (i.e., the observer’s height, projected from the local, macroscopic frame to the remote, effectively microscopic frame, where it appears as a “collapse vector”). Although horizons therefore appear to radiate, a Hawking photon is instead thought of as a “unit of projection” (of the local frame to the remote), thus challenging the notion that photons “travel through space”.
, suggesting perspectival interpretations of space, universal expansion, radiation, entanglement, gravitation, mass, dimensional reduction and measurement (as projection rather than amplification). The difference between apparent flatness of the 2-surface and actual global closure corresponds to the boson of the gauge interpretation (i.e., the observer’s height, projected from the local, macroscopic frame to the remote, effectively microscopic frame, where it appears as a “collapse vector”). Although horizons therefore appear to radiate, a Hawking photon is instead thought of as a “unit of projection” (of the local frame to the remote), thus challenging the notion that photons “travel through space”.
The paper is structured as follows. Section 2 considers the natural limit on 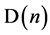 and its implications. The main geometrical characteristics of
and its implications. The main geometrical characteristics of 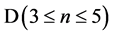 are outlined in Section 3, including a duality of the fundamental constants of GR and QM (i.e.,
are outlined in Section 3, including a duality of the fundamental constants of GR and QM (i.e., 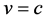 and
and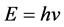 ). Section 4 interprets perspective as gauge, and Section 5 then interprets the Standard Model gauge group as perspective, with gravity included by way of charge- mass duality. Characteristics from Section 3 are then applied to black holes in Section 6 using an Alice-and-Bob scenario. A scheme for quantum gravity (QG) is outlined, together with an account of black hole entropy and an interpretation of the information paradox as a perspectival effect. Finally, Section 7 is a discussion and brief
). Section 4 interprets perspective as gauge, and Section 5 then interprets the Standard Model gauge group as perspective, with gravity included by way of charge- mass duality. Characteristics from Section 3 are then applied to black holes in Section 6 using an Alice-and-Bob scenario. A scheme for quantum gravity (QG) is outlined, together with an account of black hole entropy and an interpretation of the information paradox as a perspectival effect. Finally, Section 7 is a discussion and brief
summary of the main ideas. In terms of notation, the case in which a 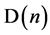 surface is spherically closed and embedded in
surface is spherically closed and embedded in 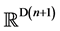 is denoted typically as
is denoted typically as![]() .
.
2. Natural Limit on D(n)
If differences are now expressed as derivatives, then the difference between two spacetime positions ![]() and
and ![]() is a change of position or velocity
is a change of position or velocity![]() , and the difference between two velocities is an acceleration
, and the difference between two velocities is an acceleration![]() , etc. At each iteration, the previously established difference is used as a new reference, and the de-
, etc. At each iteration, the previously established difference is used as a new reference, and the de-
Diminishing Freedoms
Since the observer also possesses limited freedoms, perspectival effects at ![]() (e.g., geometry, horizons) become increasingly observer-independent with each
(e.g., geometry, horizons) become increasingly observer-independent with each ![]() increment with respect to the observer; i.e., the
increment with respect to the observer; i.e., the
![]()
Figure 1. Successive iterations of a simple difference operation reach a critical threshold at![]() .
.
observer possesses diminishing freedoms with respect to physical phenomena. Therefore we define dimensionality in terms of freedoms. Whereas in ![]() the observer possesses the freedom to orientate in any superposition
the observer possesses the freedom to orientate in any superposition
of axes![]() , in
, in ![]() the observer has limited freedom to orientate in 4-space in axes
the observer has limited freedom to orientate in 4-space in axes ![]() 1, and in
1, and in
![]() , freedom is further curtailed; a body now has mass (i.e., is subject to spacetime curvature). Similarly for horizons; at
, freedom is further curtailed; a body now has mass (i.e., is subject to spacetime curvature). Similarly for horizons; at ![]() the
the ![]() planetary horizon is global (remote), surrounds the observer, and is completely observer-dependent, moving as the observer changes 2-position (i.e., is totally “permeable”). At
planetary horizon is global (remote), surrounds the observer, and is completely observer-dependent, moving as the observer changes 2-position (i.e., is totally “permeable”). At ![]() the
the ![]() cosmological horizon is also global (remote) and surrounds the observer, but is less observer-dependent, moving as the observer changes 3-position (i.e., with the observer’s velocity) but being causally “semi-permeable”. Finally, at
cosmological horizon is also global (remote) and surrounds the observer, but is less observer-dependent, moving as the observer changes 3-position (i.e., with the observer’s velocity) but being causally “semi-permeable”. Finally, at![]() , massive bodies are now subject to local (multiple)
, massive bodies are now subject to local (multiple) ![]() black hole horizons which do not surround the observer (rather, it is as though a remote, global
black hole horizons which do not surround the observer (rather, it is as though a remote, global ![]() horizon has been brought into the local frame, in some sense). The event horizon is now a strictly one-way membrane with unclear observer-dependent status; one would expect it to accelerate with the observer. (The Rindler horizon, with similar thermal properties, appears at constant 3-distance for constant acceleration.)
horizon has been brought into the local frame, in some sense). The event horizon is now a strictly one-way membrane with unclear observer-dependent status; one would expect it to accelerate with the observer. (The Rindler horizon, with similar thermal properties, appears at constant 3-distance for constant acceleration.)
3. Geometrical Characteristics
Perspective in 3-space is that effect whereby a receding object appears to shrink to an apparent point. Perspective plus curvature (e.g., on the closed surface of Earth) means that the size of the object does not go to zero before the object disappears over the horizon. At![]() , using metres as units, Alice stands with 3-height
, using metres as units, Alice stands with 3-height ![]() above the 2-surface, which is closed with constant radius of curvature
above the 2-surface, which is closed with constant radius of curvature![]() . More formally,
. More formally,
we specify a manifold ![]() that is closed with constant radius of curvature
that is closed with constant radius of curvature ![]() and embedded in
and embedded in ![]() according to the Nash theorems. At
according to the Nash theorems. At ![]() we define a 3-height
we define a 3-height ![]() and a tangent space
and a tangent space ![]() bounded at a constant distance
bounded at a constant distance ![]() from x by
from x by![]() , where
, where![]() . The manifold
. The manifold ![]() is bounded by
is bounded by![]() , where
, where ![]() at a distance along
at a distance along ![]() such that
such that![]() , where
, where ![]() is coincident with the “top” of
is coincident with the “top” of
![]() . The tangent space
. The tangent space ![]() is defined as the perception of
is defined as the perception of ![]() due to
due to ![]() in the frame of an observer located at x with
in the frame of an observer located at x with![]() . We note the following characteristics.
. We note the following characteristics.
1) Assuming![]() , the 2-surface looks flat to good approximation (Figure 2(a)).
, the 2-surface looks flat to good approximation (Figure 2(a)).
2) There is an increasing divergence between apparent flatness and actual global closure (Figure 2(b)).
3) Parallel lines on the surface (e.g., railway lines) appear to converge to an apparent D0 point or singularity on the ![]() horizon (at a distance
horizon (at a distance![]() ).
).
4) With increasing distance from Alice, objects appear to contract and space appears to expand, and Alice reasons that these rates must be exactly equivalent;![]() .
.
5) There is a ![]() dimensional reduction from Alice’s 3-height to an apparent D0 point on
dimensional reduction from Alice’s 3-height to an apparent D0 point on![]() .
.
![]()
Figure 2. The familiar geometry of the earthbound ![]() scenario.
scenario.
6) There are two such points; A, where Alice (naively) believes she is looking, and B, where she is actually looking. In 3-space, these are clearly the same point; A and B are identified![]() .
.
7) If Alice gains sufficient 3-height, she will see the D0 point singularity transform or open up to become a D1 line singularity (i.e., there is a non-zero separation, ![]() , between railway lines as they disappear over the horizon). This forced transition,
, between railway lines as they disappear over the horizon). This forced transition, ![]() , acts as a gate that reveals the embedding of
, acts as a gate that reveals the embedding of ![]() in
in ![]() (i.e., the
(i.e., the ![]() case).
case).
8) The difference between apparent flatness and actual global closure is just Alice’s local 3-height![]() , projected (and rotated through
, projected (and rotated through![]() ) to the remote,
) to the remote, ![]() horizon. (Alice’s apparent 3-height, as projected to the remote frame and seen from the local frame, is less than the thickness of the average human hair;
horizon. (Alice’s apparent 3-height, as projected to the remote frame and seen from the local frame, is less than the thickness of the average human hair;![]() .)
.)
9) The angle ![]() subtended at Alice’s eye between the true horizontal line of sight (i.e., tangential at a radius of
subtended at Alice’s eye between the true horizontal line of sight (i.e., tangential at a radius of![]() ) and a line of sight to the actual horizon is necessarily equal to that subtended at the centre of the Earth between radial lines to the locations of Alice and the horizon, so the relationship (and transition) between points A and B is proportional to and associated with those between the local observer and the remote horizon.
) and a line of sight to the actual horizon is necessarily equal to that subtended at the centre of the Earth between radial lines to the locations of Alice and the horizon, so the relationship (and transition) between points A and B is proportional to and associated with those between the local observer and the remote horizon.
10) The transition ![]() is also that from triangle (1) with
is also that from triangle (1) with![]() , to triangle (2), with
, to triangle (2), with![]() , so the transition
, so the transition ![]() is associated with the loss of the
is associated with the loss of the ![]() term.
term.
11) Observer-dependency of the S1 horizon can be expressed as the fact that 2-distance to the S1 horizon is a constant in every frame.
12) The ![]() of an object that disappears over
of an object that disappears over ![]() does not cease to exist but is “conserved” in 3-space.
does not cease to exist but is “conserved” in 3-space.
At![]() , Alice’s 4-height is taken to be velocity (rather than the Minkowski spacetime interval,
, Alice’s 4-height is taken to be velocity (rather than the Minkowski spacetime interval,![]() ). Assuming
). Assuming![]() , the 3-surface “looks flat”, but due to the existence of
, the 3-surface “looks flat”, but due to the existence of![]() , the apparent velocity of Bob, receding, “contracts” with 3-distance to some irreducible value, interpreted here as a minimum energy,
, the apparent velocity of Bob, receding, “contracts” with 3-distance to some irreducible value, interpreted here as a minimum energy,![]() . However, when Bob is at
. However, when Bob is at![]() , his velocity relative to Alice is
, his velocity relative to Alice is![]() , and so the curvature limits are the characteristic GR and QM constants,
, and so the curvature limits are the characteristic GR and QM constants, ![]() and
and![]() . At
. At ![]()
the linear expansion of spacetime with increasing 3-distance from Alice corresponds to universal expansion with constant velocity [1] [2] . We also note that observer-dependency of the S2 (cosmological) horizon can be expressed in terms of the fact that 3-distance to the S2 horizon is a constant in every frame.
At![]() , Alice’s 5-height is acceleration. Assuming
, Alice’s 5-height is acceleration. Assuming![]() , the 4-surface “feels flat”; i.e., implying a physical basis for
, the 4-surface “feels flat”; i.e., implying a physical basis for![]() , as required by the Equivalence Principle (EP), but due to the existence of
, as required by the Equivalence Principle (EP), but due to the existence of![]() , the apparent acceleration of Bob, falling towards the black hole event horizon, decreases with 4-distance to some irreducible value, interpreted here as a minimum acceleration,
, the apparent acceleration of Bob, falling towards the black hole event horizon, decreases with 4-distance to some irreducible value, interpreted here as a minimum acceleration,![]() . At the same time, Bob’s acceleration relative to Alice is
. At the same time, Bob’s acceleration relative to Alice is![]() , where
, where ![]() is an effective maximum beyond which the Unruh or Hawking radiation wavelength is
is an effective maximum beyond which the Unruh or Hawking radiation wavelength is ![]() (i.e., a firewall) and so the curvature limits are
(i.e., a firewall) and so the curvature limits are ![]() and
and![]() . At
. At![]() , the second-order expansion of spacetime with increasing 3-distance corresponds to accelerating universal expansion [3] [4] . We also note that observer-dependency of the S3 (black hole) horizon can be expressed as the fact that 4-distance (v = c) to the S3 horizon is a constant in every frame. Thus the fixed 4-distance
, the second-order expansion of spacetime with increasing 3-distance corresponds to accelerating universal expansion [3] [4] . We also note that observer-dependency of the S3 (black hole) horizon can be expressed as the fact that 4-distance (v = c) to the S3 horizon is a constant in every frame. Thus the fixed 4-distance ![]() to the
to the![]() black hole event horizon in the local, macroscopic frame is the quantum of energy
black hole event horizon in the local, macroscopic frame is the quantum of energy ![]() in the remote, effectively microscopic frame. In this sense, then,
in the remote, effectively microscopic frame. In this sense, then, ![]() 2.
2.
4. Perspective as Gauge
Alice and Bob are astronauts moving away from each other in empty space, and, for the purposes of this consideration, we assume that neither has any prior spatial understanding. Alice first notes that Bob appears to be shrinking. Since they disagree on who is shrinking, they each theorise the existence of an embedding 3-space ![]() that makes sense of the fact that, with increasing distance, objects appear to contract (CON) and space appears to expand (EXP). Now as observers on Earth (but still without any geometrical understanding) Alice and Bob stand with equal 3-height
that makes sense of the fact that, with increasing distance, objects appear to contract (CON) and space appears to expand (EXP). Now as observers on Earth (but still without any geometrical understanding) Alice and Bob stand with equal 3-height ![]() above the 2-surface, which is closed with constant radius of curvature
above the 2-surface, which is closed with constant radius of curvature![]() . Alice is directly aware of the existence of the 2-space, but has to infer (e.g., using parallax) the existence of a higher, 3-space. Assuming
. Alice is directly aware of the existence of the 2-space, but has to infer (e.g., using parallax) the existence of a higher, 3-space. Assuming![]() , the 2-surface looks flat, so Alice does not recognise
, the 2-surface looks flat, so Alice does not recognise ![]() as an horizon, but merely as a “dimensional separation”. Therefore the significance of 3-height (or potential) and its relation to the horizon remains unacknowledged. In other words, Alice does not recognise Earth as an object.
as an horizon, but merely as a “dimensional separation”. Therefore the significance of 3-height (or potential) and its relation to the horizon remains unacknowledged. In other words, Alice does not recognise Earth as an object.
However, from outside her frame, we can see that the difference in her frame between apparent flatness and actual global closure is just the potential![]() , projected (and rotated through
, projected (and rotated through![]() ) to the remote horizon, represented by the “collapse” vector R in Figure 2(b). Now Alice and Bob disagree about shrinkage and phase, which vary from point to point. In gauge terms, the 2-surface is the base space
) to the remote horizon, represented by the “collapse” vector R in Figure 2(b). Now Alice and Bob disagree about shrinkage and phase, which vary from point to point. In gauge terms, the 2-surface is the base space![]() , and the unacknowledged potential is the fibre
, and the unacknowledged potential is the fibre![]() , defining an internal space at each point on
, defining an internal space at each point on ![]() which together comprise a fibre bundle,
which together comprise a fibre bundle, ![]() , such that
, such that![]() . The gauge field comprises gauge connections that correspond to the group
. The gauge field comprises gauge connections that correspond to the group ![]() of continuous symmetries of
of continuous symmetries of![]() , and in that there is a canonical projection, submersion or surjective map,
, and in that there is a canonical projection, submersion or surjective map, ![]() , then the phase
, then the phase ![]() is a continuous image of
is a continuous image of ![]() in
in![]() . Thus, R is just the potential
. Thus, R is just the potential![]() , projected from the local to the remote frame, that appears in Alice’s frame as a “minimum unit” (i.e., the gauge boson or field quantum) that is the coupling constant or interaction strength that translates between frames and restores local gauge
, projected from the local to the remote frame, that appears in Alice’s frame as a “minimum unit” (i.e., the gauge boson or field quantum) that is the coupling constant or interaction strength that translates between frames and restores local gauge
invariance. Alice also notes that as she and Bob stand at each other’s horizon, the values 2 and ![]() define curvature limits at
define curvature limits at![]() , allowing this geometry to be applied to
, allowing this geometry to be applied to![]() .
.
5. Gauge as Perspective
The Standard Model (SM) is the non-Abelian gauge group ![]() that describes particles and interactions in terms of a sequence of early-epoch phase transitions following a Big Bang at
that describes particles and interactions in terms of a sequence of early-epoch phase transitions following a Big Bang at![]() . In the perspective approach, the SM comprises two groups of sets of
. In the perspective approach, the SM comprises two groups of sets of ![]() perspective reductions. The first is
perspective reductions. The first is![]() , where
, where ![]() are derivatives,
are derivatives,![]() . These generate apparent Planck dimension perspectival convergence limits
. These generate apparent Planck dimension perspectival convergence limits ![]() (with
(with![]() ), which are interpreted as fermions. At each
), which are interpreted as fermions. At each ![]() level, a
level, a ![]() height is associated with spherical closure of
height is associated with spherical closure of![]() , forming a series of “onion layers”, where each closure
, forming a series of “onion layers”, where each closure ![]() generates
generates ![]() -forms that populate
-forms that populate ![]() space;
space; ![]() (i.e., a string), etc, as depicted in Figure 3. The second group is
(i.e., a string), etc, as depicted in Figure 3. The second group is![]() , generating apparent D2 area
, generating apparent D2 area ![]() singularities that live on the
singularities that live on the ![]() horizon separating
horizon separating![]() , interpreted as the leptons, the 2-forms that in the SM are “cousins” to quarks.
, interpreted as the leptons, the 2-forms that in the SM are “cousins” to quarks.
Assuming ![]() at each level, each
at each level, each ![]() surface can be described as a state defined by n direc-
surface can be described as a state defined by n direc-
tions or generators, so each lower level can be thought of as a state-splitting or copying process producing families of ![]() generations; e.g., the Cabibbo-Kobayashi-Maskawa matrix describing expectation-values for transitions between families and generations of quarks (with the Cabibbo angle corresponding to probabilities of decay modes), and the Pontecorvo-Maki-Nakagawa-Sakata matrix summarising weightings for lepton-mixing. The superpositions of directions (generators) at higher
generations; e.g., the Cabibbo-Kobayashi-Maskawa matrix describing expectation-values for transitions between families and generations of quarks (with the Cabibbo angle corresponding to probabilities of decay modes), and the Pontecorvo-Maki-Nakagawa-Sakata matrix summarising weightings for lepton-mixing. The superpositions of directions (generators) at higher ![]() are rotations that transform lower
are rotations that transform lower ![]() particles, as depicted in Figure 4.
particles, as depicted in Figure 4.
![]()
Figure 3. Two groups of ![]() reductions generate an “onion-layer” model of particles and interactions, and juxtapose quarks and leptons (dashed line).
reductions generate an “onion-layer” model of particles and interactions, and juxtapose quarks and leptons (dashed line).
Each inter-dimension or phase transition is a ![]() perspective reduction; at each level, a
perspective reduction; at each level, a ![]() -form possesses a local
-form possesses a local ![]() height (a property defined by that internal space), from which there is an apparent diminishing of
height (a property defined by that internal space), from which there is an apparent diminishing of ![]() until it disappears over the associated
until it disappears over the associated ![]() horizon. Thus,
horizon. Thus, ![]() colour bleaches
colour bleaches
out of Quark-world as quarks “fall into Quark-world black holes” (i.e., inside-out hadrons), which is the process of baryogenesis, marking the global closure of D2, the formation of colour-neutral baryons and the conservation of colour. Likewise, charge bleaches out of Nucleus-world as “nuclei fall into Nucleus-world black holes” (i.e., electrons, or inside-out atoms), corresponding to the formation of charge-neutral atoms and the conservation of charge at global closure of D4. In the perspective model at![]() , information bleaches out of the (D4) universe as an SM phase transition. In QED, the atomic nucleus containing positively charged protons is sur-
, information bleaches out of the (D4) universe as an SM phase transition. In QED, the atomic nucleus containing positively charged protons is sur-
rounded and perfectly balanced by shells populated by negatively charged electrons;![]() . The 5-height of
. The 5-height of
the nucleus connects via D(n − 3) perspective reduction to a Dirac spinor of the Penrose zigzag electron, ![]() [5] in the last electron shell. In the nucleus frame, assuming
[5] in the last electron shell. In the nucleus frame, assuming![]() , the separation of equally spaced calibrations of the n-surface appears to decrease with increasing distance and so the exact location of the
, the separation of equally spaced calibrations of the n-surface appears to decrease with increasing distance and so the exact location of the ![]() horizon is uncertain, and electron shells are thus interpreted as multiple
horizon is uncertain, and electron shells are thus interpreted as multiple ![]() horizons. The quantum state
horizons. The quantum state
of the atom is defined as a superposition of all shells, or![]() , in which
, in which ![]() are the eigenstates of an observable (e.g., the principle quantum number, n) corresponding to eigenvalues
are the eigenstates of an observable (e.g., the principle quantum number, n) corresponding to eigenvalues![]() .
.
Electromagnetism-Gravitation Duality
Given the correspondence between ![]() at the macroscopic level and
at the macroscopic level and ![]() at the microscopic level, we now ask if there is a precedent for the notion of charge at the macroscopic scale. We note that mass tends towards horizons; either expanding (state; EXP) as part of the Hubble flow towards the
at the microscopic level, we now ask if there is a precedent for the notion of charge at the macroscopic scale. We note that mass tends towards horizons; either expanding (state; EXP) as part of the Hubble flow towards the ![]() cosmological horizon, or contracting (state; CON) towards
cosmological horizon, or contracting (state; CON) towards ![]() black hole event horizons (Figure 5). In Alice’s
black hole event horizons (Figure 5). In Alice’s ![]() frame, the rates
frame, the rates
must be exactly equal;![]() . Such labelling is arbitrary and therefore cannot be defined in any absolute way. In gauge-theoretic terms, just as the photon expresses the fact that we cannot define charge in an absolute sense in the Coulomb gauge, so the graviton would be the gauge particle mediating between EXP and CON “charges”3.
. Such labelling is arbitrary and therefore cannot be defined in any absolute way. In gauge-theoretic terms, just as the photon expresses the fact that we cannot define charge in an absolute sense in the Coulomb gauge, so the graviton would be the gauge particle mediating between EXP and CON “charges”3.
Generalising Newton’s third law, any derivative of action-force ![]() applied to a massive body (regardless of mass or composition) will elicit an instantaneous, exactly equivalent and perfectly counter-di- rected reaction-force,
applied to a massive body (regardless of mass or composition) will elicit an instantaneous, exactly equivalent and perfectly counter-di- rected reaction-force,![]() . Therefore, the picture suggested is of a massive 3-object (a CON
. Therefore, the picture suggested is of a massive 3-object (a CON
charge) surrounded by “derivative shells” populated by black holes. The ![]() of the 3-object is perfectly balanced by the
of the 3-object is perfectly balanced by the ![]() of the derivative shells, and so the QG definition of freefall would be the superposition of all derivative shells. Therefore mass at the macroscopic level is charge at the microscopic level. In the perspective model, projection of height in the local, macroscopic frame to the remote (effectively) microscopic frame becomes more real, until, at the level of maximum physical reality, it is effectively real. That means that the observer is effectively projected into the microscopic domain, implying a thorough mixing of macroscopic and microscopic scales, and, somewhat outrageously, that electrons are black holes.
of the derivative shells, and so the QG definition of freefall would be the superposition of all derivative shells. Therefore mass at the macroscopic level is charge at the microscopic level. In the perspective model, projection of height in the local, macroscopic frame to the remote (effectively) microscopic frame becomes more real, until, at the level of maximum physical reality, it is effectively real. That means that the observer is effectively projected into the microscopic domain, implying a thorough mixing of macroscopic and microscopic scales, and, somewhat outrageously, that electrons are black holes.
Black hole-electron duality (as suggested in [8] - [10] ) opens up many further correspondences. For instance, QED vacuum polarisation, in which the bare electron charge is dressed by slight displacement of virtual ![]() pairs away from and towards the charge, respectively, would correspond to GR vacuum polarisation, in
pairs away from and towards the charge, respectively, would correspond to GR vacuum polarisation, in
which the bare black hole “EXP” charge is dressed by displacement of virtual charges, dark energy ![]() and dark matter
and dark matter![]() , respectively. Also, QED renormalisation, in which the cancellation of divergent inter-
, respectively. Also, QED renormalisation, in which the cancellation of divergent inter-
grals may be achieved by removing the electron interior region ![]() (where
(where ![]() is the classical radius) would suggest that gravitational renormalisation would be likewise achieved by removal of the black hole interior region,
is the classical radius) would suggest that gravitational renormalisation would be likewise achieved by removal of the black hole interior region,![]() .
.
We might also note that the perspective projection ![]() maps the local, macroscopic (black hole) frame to the SM photon epoch following nucleosynthesis but before ions gained electrons. At this time, the densities of relativistic radiation (photons) and non-relativistic matter (atomic nuclei) were equal. The subsequent decoupling of matter and radiation and the formation of charge-neutral atoms corresponds in the perspective model to the global closure of D4. At recombination (the surface of last scattering), the photon mean path length became effectively infinite, and the Universe thus became transparent. At the macroscopic scale, the coincidence (or “why now?”) problem asks why the energy densities of dark energy (i.e., the cosmological constant)
maps the local, macroscopic (black hole) frame to the SM photon epoch following nucleosynthesis but before ions gained electrons. At this time, the densities of relativistic radiation (photons) and non-relativistic matter (atomic nuclei) were equal. The subsequent decoupling of matter and radiation and the formation of charge-neutral atoms corresponds in the perspective model to the global closure of D4. At recombination (the surface of last scattering), the photon mean path length became effectively infinite, and the Universe thus became transparent. At the macroscopic scale, the coincidence (or “why now?”) problem asks why the energy densities of dark energy (i.e., the cosmological constant)
and matter should be comparable. This suggests a perspective map![]() , from the
, from the
coincidence problem at the macroscopic scale to the pre-decoupling radiation-matter densities of the SM. In the perspective approach, gravitons at the macroscopic scale are photons at the microscopic scale, in which case, the experimental absence of gravitons would indicate that the Universe is not “yet” gravitationally transparent. We next consider black holes, the firewall question and the information paradox.
6. Black Holes
6.1. Background
If Hawking radiation is thermal [11] , then the scattering matrix is nonunitary. Complementarity allows information to exist in the exterior and interior regions as long as observers cannot compare notes [12] [13] , but the “AMPS” paper [14] showed inconsistencies in the theory’s postulates, reasoning that if evaporation is unitary and maximal entanglement is monogamous, early radiation (C) and late radiation (B) must be entangled, giving rise to a firewall at ![]() where entanglement between B and interior modes (A) is broken, or if the EP is to be preserved, then B must be only entangled with A, at the expense of unitarity. The
where entanglement between B and interior modes (A) is broken, or if the EP is to be preserved, then B must be only entangled with A, at the expense of unitarity. The ![]() solution [15] is a duality between Einstein-Rosen bridges and EPR entanglement that allows entanglement of A and B (ensuring no drama), and entanglement of B and C via ER bridges (ensuring unitarity). Given certain computational complexity assumptions [16] , Alice, by measuring Hawking radiation, generates a shockwave [17] in the ER bridge, thereby inducing a firewall in the remote black hole throat.
solution [15] is a duality between Einstein-Rosen bridges and EPR entanglement that allows entanglement of A and B (ensuring no drama), and entanglement of B and C via ER bridges (ensuring unitarity). Given certain computational complexity assumptions [16] , Alice, by measuring Hawking radiation, generates a shockwave [17] in the ER bridge, thereby inducing a firewall in the remote black hole throat.
6.2. Perspective Model Interpretation
The effects listed in Section 2 may be demonstrated using Alice and Bob, in orbit around a massive black hole. They synchronise clocks and Alice remains in orbit while Bob begins his radial freefall descent towards the black hole. The effective divergence between their frames (![]() and
and![]() ) is due to the fact that Bob is commoving with global accelerated expansion towards the local
) is due to the fact that Bob is commoving with global accelerated expansion towards the local![]() , at which
, at which ![]() 4. Just as at
4. Just as at![]() , apparent 3-height decreases with distance, so at
, apparent 3-height decreases with distance, so at ![]() in Alice’s frame, Bob’s apparent acceleration decreases as he approaches
in Alice’s frame, Bob’s apparent acceleration decreases as he approaches![]() . The photons comprising his image redshift to
. The photons comprising his image redshift to![]() , and Alice sees Bob hover (and therefore surmises that he must then burn up as a consequence of the EP). Calculating for the huge Lorentz
, and Alice sees Bob hover (and therefore surmises that he must then burn up as a consequence of the EP). Calculating for the huge Lorentz
and gravitational boosts, Alice records the exact time in her frame ![]() that Bob “actually” crosses
that Bob “actually” crosses![]() . In Bob’s frame, the coordinate singularity
. In Bob’s frame, the coordinate singularity ![]() does not exist. Due to
does not exist. Due to![]() , the 4-mani- fold feels flat, and so the apparent area singularity
, the 4-mani- fold feels flat, and so the apparent area singularity ![]() remains on the
remains on the ![]() horizon at all times. (In Hamil-
horizon at all times. (In Hamil-
ton’s analysis [19] , the illusory horizon recedes in front of Bob until he finally merges with it in finite time at![]() .) The difference between apparent flatness (the tangent space,
.) The difference between apparent flatness (the tangent space,![]() ) and actual global closure is just the observer’s local 5-height (acceleration, or mass), projected to the remote horizon, where it appears as the gauge boson. Classically, one would say that geometry radiates, and assuming minimal 5-height (acceleration) due to
) and actual global closure is just the observer’s local 5-height (acceleration, or mass), projected to the remote horizon, where it appears as the gauge boson. Classically, one would say that geometry radiates, and assuming minimal 5-height (acceleration) due to![]() , then Hawking radiation (HR) is also minimal (i.e.,
, then Hawking radiation (HR) is also minimal (i.e.,![]() ). However, in the perspective model, the more fundamental picture is projection of the local to the remote frame; the boson is the “unit of projection”, so, strictly speaking, photons do not travel. Spatial extent is therefore emergent and the “3-ness” of space is just the fact of
). However, in the perspective model, the more fundamental picture is projection of the local to the remote frame; the boson is the “unit of projection”, so, strictly speaking, photons do not travel. Spatial extent is therefore emergent and the “3-ness” of space is just the fact of ![]() reduction; “space” is then thought of as the absence of intervening dimensionality.
reduction; “space” is then thought of as the absence of intervening dimensionality.
At some point, Bob begins to experience tidal deformation. Now, according to the Correspondence Principle (CP), classical dynamics (typified by Newton’s![]() ) is recovered in the statistical limit and for well-de- fined wavepackets from quantum dynamics (typified by the Schrödinger equation,
) is recovered in the statistical limit and for well-de- fined wavepackets from quantum dynamics (typified by the Schrödinger equation,![]() ),
),
and so the CP must therefore also relate the respective GR and QM “charges”, mass and information, and the associated dynamics (acceleration and measurement) by which each is registered. This validates a comparison between black holes and the slits in the Young double-slit experiment. Assuming no which-path detection, then in the frame of the emitted particle, the slits themselves must become superposed or wavelike. Therefore, if interference fringes are to appear, then just as the particle cannot “know” by which slit it is entering the set-up, so Bob cannot know towards which black hole he is falling. Bob is therefore falling into N black holes and the tidal forces (fluctuations and oscillations) he experiences represent the superposition of distinct black hole spacetime
geometries;![]() . (One would also expect that this gravi-
. (One would also expect that this gravi-
tational interference or “Weyl field” of gravitational nonuniformity, corresponding to the interference in the double-slit set-up, would be exactly obscured from Alice’s view by the Lorentz and gravitational shifts in her
frame.) However, due to![]() , the 4-surface feels flat (i.e., Bob never experiences his own mass), and the apparent area singularity
, the 4-surface feels flat (i.e., Bob never experiences his own mass), and the apparent area singularity ![]() towards which he is falling therefore never leaves the
towards which he is falling therefore never leaves the ![]() horizon.
horizon.
6.3. Scheme for QG and the Information Paradox
As Bob reaches the singularity in his frame in finite time, had his clock been intact, it would have recorded ex-
actly![]() . Thus the “central singularity” and “event horizon” are both horizons and are identified;
. Thus the “central singularity” and “event horizon” are both horizons and are identified;![]() ; i.e., the apparent separation of points A and B becomes more real and is the physical basis
; i.e., the apparent separation of points A and B becomes more real and is the physical basis
for entanglement. One would then expect that the IR cut-off in Alice’s frame is directly proportional to the UV cut-off as Bob hits the singularity at effective perspectival convergence in his frame (which we think of as![]() ). Therefore Hawking radiation corresponds to the collapse vector R, so
). Therefore Hawking radiation corresponds to the collapse vector R, so![]() , and
, and ![]() is just
is just ![]() “writ large”, thus obviating the need for tunnelling or cosmological protection, since all “central singularities” must be “exposed” in this way.
“writ large”, thus obviating the need for tunnelling or cosmological protection, since all “central singularities” must be “exposed” in this way.
At![]() , the
, the ![]() reduction is from
reduction is from ![]() to an apparent area
to an apparent area ![]() singularity (at the macroscopic level, a black hole microstate, and at the microscopic level, a Dirac electron spinor). At
singularity (at the macroscopic level, a black hole microstate, and at the microscopic level, a Dirac electron spinor). At![]() , the
, the ![]()
reduction is from ![]() to an apparent
to an apparent ![]() singularity (at the macroscopic level, a black hole, and at the microscopic level, an electron). Therefore, inter-electron spacing (charge quantisation) is defined in terms of photons, and inter-black hole spacing (gravitational quantisation) is defined in terms of gravitons. To non-gravita- tionally accelerate is to gain extra 5-height and thereby to force the
singularity (at the macroscopic level, a black hole, and at the microscopic level, an electron). Therefore, inter-electron spacing (charge quantisation) is defined in terms of photons, and inter-black hole spacing (gravitational quantisation) is defined in terms of gravitons. To non-gravita- tionally accelerate is to gain extra 5-height and thereby to force the ![]() transition and reveal the
transition and reveal the ![]() embedding (a photon). Likewise, to measure is to gain extra 8-height and thereby to force the
embedding (a photon). Likewise, to measure is to gain extra 8-height and thereby to force the ![]() transition, revealing the
transition, revealing the ![]() embedding (a graviton). (The act of measurement is therefore not one of “amplification” from the microscopic, quantum frame up to the macroscopic, classical frame, but one of projection in the opposite direction.) Thus to measure a black hole is effectively to overlay the transition
embedding (a graviton). (The act of measurement is therefore not one of “amplification” from the microscopic, quantum frame up to the macroscopic, classical frame, but one of projection in the opposite direction.) Thus to measure a black hole is effectively to overlay the transition ![]() onto
onto![]() . Therefore, for Alice to measure any property of a black hole is to generate a shockwave [17] in the ER bridge between black hole throats in the maximally extended Schwarzchild solution, or to reveal the identification of the apparent D5 singularity
. Therefore, for Alice to measure any property of a black hole is to generate a shockwave [17] in the ER bridge between black hole throats in the maximally extended Schwarzchild solution, or to reveal the identification of the apparent D5 singularity ![]() (point A) with the actual D6 singularity
(point A) with the actual D6 singularity ![]() (point B) and thereby produce a graviton (manifesting as a firewall) in the opposite throat.
(point B) and thereby produce a graviton (manifesting as a firewall) in the opposite throat.
For interference to occur in the double-slit set-up, the separate eigenstates representing the outcomes in which the particle passed through ![]() or
or ![]() are quantum linearly superposed; i.e., the wavefunction describes both states,
are quantum linearly superposed; i.e., the wavefunction describes both states, ![]() , where
, where ![]() is the phase difference between the two paths. In the perspective model, a body’s mass is the projection of its local 5-height to the remote frame, where it appears as the body’s highly contracted (Schwarzchild) radius,
is the phase difference between the two paths. In the perspective model, a body’s mass is the projection of its local 5-height to the remote frame, where it appears as the body’s highly contracted (Schwarzchild) radius, ![]() , so
, so![]() . Since points A
. Since points A
![]() and B
and B ![]() are entangled horizons (i.e., identified), there is a spacetime path-length difference (phase) between frames
are entangled horizons (i.e., identified), there is a spacetime path-length difference (phase) between frames ![]() and
and ![]() (so
(so![]() ). By measuring the black hole, Alice is in effect deriving which-path information, destroying Weyl interference (i.e., the loss of the
). By measuring the black hole, Alice is in effect deriving which-path information, destroying Weyl interference (i.e., the loss of the ![]() term in Figure 2(b)) and thereby quantising the gravitational field. It was Einstein’s happiest thought [20] - [22] that gravity is eliminated in a freely falling frame, and whilst classically, tidal forces cannot be gauged away, quantum gravitationally they are eliminated. In Alice’s frame, Bob enters the graviton frame at
term in Figure 2(b)) and thereby quantising the gravitational field. It was Einstein’s happiest thought [20] - [22] that gravity is eliminated in a freely falling frame, and whilst classically, tidal forces cannot be gauged away, quantum gravitationally they are eliminated. In Alice’s frame, Bob enters the graviton frame at![]() , and, since no time elapses in the graviton frame, is instantly transported to
, and, since no time elapses in the graviton frame, is instantly transported to![]() , and in his own frame, due to the temporal phase, he reaches
, and in his own frame, due to the temporal phase, he reaches ![]() and is instantly transported to
and is instantly transported to ![]() (i.e., in the conformally invariant limit, mass and time have no
(i.e., in the conformally invariant limit, mass and time have no
meaning [7] ). At![]() , an object that disappears over the
, an object that disappears over the ![]() horizon does not cease to exist but is conserved in 3-space. Likewise, “falling into a black hole” is just a
horizon does not cease to exist but is conserved in 3-space. Likewise, “falling into a black hole” is just a ![]() reduction, or projection from the local, macroscopic frame (Bob) to the remote, effectively microscopic frame
reduction, or projection from the local, macroscopic frame (Bob) to the remote, effectively microscopic frame![]() . Therefore, the information
. Therefore, the information
content of infalling matter defined in terms of inter-electron connectivity (i.e., photons) becomes inter-black hole connectivity (i.e., gravitons). In other words, information is preserved in ![]() (or more correctly,
(or more correctly,![]() ), as gravitons exchanged by black holes “in black hole space” (in our D4 frame we might say “inside black holes”, e.g., see [23] - [26] ).
), as gravitons exchanged by black holes “in black hole space” (in our D4 frame we might say “inside black holes”, e.g., see [23] - [26] ).
6.4. The Origin of Black Hole Entropy
The limit principle implies a “maximum physical reality” at D6, that D7 is therefore non-physical (i.e., mathematical) and that D8 is in some appropriate sense “beyond” mathematics (i.e., noncomputable). In the perspective model, Alice’s highest freedom (i.e., her measurement independence, which by definition must be noncomputable [27] ) is effectively projected into the remote frame where it appears as quantum indeterminacy. At![]() , local 5-height projected into the remote frame appears at the microscopic level as the coupling constant
, local 5-height projected into the remote frame appears at the microscopic level as the coupling constant ![]() linking the Dirac spinors of the zigzag electron [5] , and at the macroscopic level as the Schwarzchild radius
linking the Dirac spinors of the zigzag electron [5] , and at the macroscopic level as the Schwarzchild radius ![]() linking what in the conventional picture are
linking what in the conventional picture are ![]() and
and![]() . At
. At![]() , local 8-
, local 8-
height projected into the remote frame appears at the microscopic level as EPR entanglement (the identification![]() ), and at the macroscopic level as an ER bridge. At
), and at the macroscopic level as an ER bridge. At![]() , an object that disappears over
, an object that disappears over ![]() and returns from the opposite 2-space direction demonstrates spherical closure of the 2-surface. Likewise, at
and returns from the opposite 2-space direction demonstrates spherical closure of the 2-surface. Likewise, at![]() , to accelerate is to gain extra 5-height, to see closure of D4 and, by Newton’s third law, to invoke an equal and opposite reaction in which the by-product is heat (the fall-off of energy usefulness). At
, to accelerate is to gain extra 5-height, to see closure of D4 and, by Newton’s third law, to invoke an equal and opposite reaction in which the by-product is heat (the fall-off of energy usefulness). At![]() , to measure is to gain extra 8-height, to see closure of D7 [28] and, by a quantum third law, to invoke an “equal and opposite reaction” (e.g., spin measured along the z-axes of spacelike separated EPR-entangled particles), in which the by- product is entropy (the fall-off of information usefulness). In other words, “physical reality” must demonstrate at least the same degree of freedom in its response to measurement, as proposed in [29] .
, to measure is to gain extra 8-height, to see closure of D7 [28] and, by a quantum third law, to invoke an “equal and opposite reaction” (e.g., spin measured along the z-axes of spacelike separated EPR-entangled particles), in which the by- product is entropy (the fall-off of information usefulness). In other words, “physical reality” must demonstrate at least the same degree of freedom in its response to measurement, as proposed in [29] .
In the perspective model, a black hole is just the difference between spacetime path lengths; i.e., the effective separation of points A and B (conventionally, ![]() and
and![]() ), which is just
), which is just![]() . For the freely falling asymptotic Alice, the apparent convergence limit
. For the freely falling asymptotic Alice, the apparent convergence limit ![]() represents a Hawking photon, or unit of projection.
represents a Hawking photon, or unit of projection.
(Since freefall presumes minimum 5-height, the “emission rate” is also minimal;![]() .)The infalling Bob encounters the perspectival convergence limit
.)The infalling Bob encounters the perspectival convergence limit ![]() in his frame as a graviton (a firewall, or surface of maximum acceleration) at so-called
in his frame as a graviton (a firewall, or surface of maximum acceleration) at so-called![]() . Therefore,
. Therefore, ![]() is a measure of how many
is a measure of how many ![]() projection-units (Hawking photons) it takes (via
projection-units (Hawking photons) it takes (via![]() ) to disperse the black hole’s mass, and
) to disperse the black hole’s mass, and ![]()
is a measure of how many ![]() projection-units (inter-black hole gravitons) it takes to disperse the black hole’s information. However, by projection or by infall (i.e., by
projection-units (inter-black hole gravitons) it takes to disperse the black hole’s information. However, by projection or by infall (i.e., by ![]() reduction), a black hole is both a macroscopic and a microscopic entity, and therefore the path length difference (i.e., the separation of
reduction), a black hole is both a macroscopic and a microscopic entity, and therefore the path length difference (i.e., the separation of ![]()
and![]() ) isa maximum of one graviton;
) isa maximum of one graviton;![]() . Thus a single graviton or unit of spacetime uncertainty accounts for the entire
. Thus a single graviton or unit of spacetime uncertainty accounts for the entire ![]() distance (measured as noncomputability), which is of course proportional to entropy, expressed as
distance (measured as noncomputability), which is of course proportional to entropy, expressed as ![]() and calculated at
and calculated at ![]() [11] [30] . This many-to-one reduction is an instance of the fact that quantum measurement reduces multiple complex-weighted, linearly superposed alternatives to a single classical outcome (in accordance with the Born rule,
[11] [30] . This many-to-one reduction is an instance of the fact that quantum measurement reduces multiple complex-weighted, linearly superposed alternatives to a single classical outcome (in accordance with the Born rule,![]() ).
).
Bob (or what remains of his body) always reaches the so-called ![]() (and is transported to the so-called
(and is transported to the so-called![]() , due to
, due to![]() )5. Since he experiences no drama, the EP is not violated. Noting the similarity of the EP and a black hole (roughly, that neither reveals composition), it seems reasonable to claim that, since the EP is never violated, Hawking radiation cannot contain quantum information (i.e., is completely thermal).Information “loss” is then seen as an SM phase transition. Just as
)5. Since he experiences no drama, the EP is not violated. Noting the similarity of the EP and a black hole (roughly, that neither reveals composition), it seems reasonable to claim that, since the EP is never violated, Hawking radiation cannot contain quantum information (i.e., is completely thermal).Information “loss” is then seen as an SM phase transition. Just as ![]() colour bleaches out of Quarkworld (to be conserved in the form of colour-neutral hadrons), so electric charge (
colour bleaches out of Quarkworld (to be conserved in the form of colour-neutral hadrons), so electric charge (![]() ) bleaches out of D4 (to be conserved in the form of charge-neutral atoms defined in terms of photon-exchange between electrons), and “mass charge” (CON, EXP) bleaches out of D4 (to be conserved in the form of mass-charge-neutral “cosmic atoms” defined in terms of graviton-exchange between black holes).
) bleaches out of D4 (to be conserved in the form of charge-neutral atoms defined in terms of photon-exchange between electrons), and “mass charge” (CON, EXP) bleaches out of D4 (to be conserved in the form of mass-charge-neutral “cosmic atoms” defined in terms of graviton-exchange between black holes).
7. Discussion and Summary
One would like to explore a number of further implications of the perspective model, including;
1) that the “geometry of time” (i.e., a potential ![]() above a spherically closed spacetime surface
above a spherically closed spacetime surface![]() ) is common to GR (classical spacetime at
) is common to GR (classical spacetime at![]() ) and QM (quantum spacetime at
) and QM (quantum spacetime at![]() ),
),
2) that apparent flatness and collapse correspond to the U and R processes of QM,
3) that at![]() , assuming
, assuming![]() , quantum superposed alternatives are multiple
, quantum superposed alternatives are multiple ![]() -collapse thresholds (
-collapse thresholds (![]() horizons) at one-graviton spacings, and that Schrödinger cat states collapse when associated spacetime curvature reaches a threshold of
horizons) at one-graviton spacings, and that Schrödinger cat states collapse when associated spacetime curvature reaches a threshold of ![]() [26] .
[26] .
4) that if black holes correspond to paths, impacts on the second screen of the double-slit set-up should replicate the distribution of black holes in that direction,
5) that Newton’s third law may be applied to EPR entanglement, in that the outcome of a measurement of spin along the z-axis of one entangled particle is perfectly correlated by the opposite outcome of a measurement of spin along the z-axis of the spacelike separated particle,
6) that, as at![]() , apparent 3-height is maximum in the local frame and projected to an apparent minimum in the remote frame, so at
, apparent 3-height is maximum in the local frame and projected to an apparent minimum in the remote frame, so at![]() , the local “rate at which time passes” (i.e., maximised proper time,
, the local “rate at which time passes” (i.e., maximised proper time,![]() ) is projected to the remote frame and juxtaposed with “cosmic” time,
) is projected to the remote frame and juxtaposed with “cosmic” time,
7) that the projection of local (macroscopic) values into the remote (effectively microscopic) frame explains apparent fine-tuning, naturalness, hierarchy and large number problems.
To summarise, the two principle ![]() reductions (
reductions (![]() and
and![]() ) and the two scale extremes (i.e., macroscopic and microscopic) define four sectors (Figure 6).
) and the two scale extremes (i.e., macroscopic and microscopic) define four sectors (Figure 6).
Acknowledgements
I am extremely grateful to Arkady Bolotin (Ben Gurion University of the Negev) for his comments, advice and patience.
NOTES
![]()
1If time is treated as an imaginary coordinate![]() , the Lorentz transformation
, the Lorentz transformation ![]() can be thought of as a rotation in Euclidean 4-space,
can be thought of as a rotation in Euclidean 4-space,![]() .
.
2The author is not aware that a direct equivalence has been proposed in previous works by other authors.
3It is noteworthy that in Penrose’s Conformal Cyclic Cosmology model [6] [7] , conformal invariance prevails both near an initial singularity and at a future state of maximum spatial expansion (future boundary hypersurface![]() ), thus the state of maximum expansion is converted to the state of maximum contraction.
), thus the state of maximum expansion is converted to the state of maximum contraction.
4In Hamilton’s river model [18] , spacetime is in effect pouring over the edge of spacetime at![]() .
.
5The graviton as “unit of spacetime uncertainty” accounts for what would otherwise be a causality-violating, backwards-in-time jump.