Influence of C-Axis Inter Unit Cell Resonant Tunneling on the Spectral Function in Bilayer Cuprates ()
1. Introduction
The angle resolved photoemission spectroscopic (ARPES) measurements [1,2] have emerged as dependable and useful tools for understanding the electronic structure of layered cuprates. In comparison to the single layer per unit cell material such as La2−xSrxCuO4, the ARPES spectra of bilayer cuprates such as Bi2Sr2CaCu2O8+x(Bi-2212) showed a splitting of spectral function along the antinodal point of the Brillouin zone. A number of experiments are performed to study the band splitting in Bi-2212 which has two Cu-O planes within its unit cell [3-6]. The splitting is found to be large in normal state, with the maximum splitting (~110 MeV) at ( ,0) point of the Brillouin zone. It is also pointed out that the normal state of cuprates shows broadening in the spectral function while sharp and prominent spectral features are observed in the superconducting state. The splitting in the electronic states is attributed to the coupling between the Cu-O planes within the unit cell. The absence of band splitting in cuprates having only one Cu-O layer per unit cell gives credence to the hypothesis that there must be some sort of out-of-plane effect on account of interlayer coupling in cuprates where there are more than one Cu-O planes per unit cell.
,0) point of the Brillouin zone. It is also pointed out that the normal state of cuprates shows broadening in the spectral function while sharp and prominent spectral features are observed in the superconducting state. The splitting in the electronic states is attributed to the coupling between the Cu-O planes within the unit cell. The absence of band splitting in cuprates having only one Cu-O layer per unit cell gives credence to the hypothesis that there must be some sort of out-of-plane effect on account of interlayer coupling in cuprates where there are more than one Cu-O planes per unit cell.
Several authors have emphasized [7-10] the role of intra cell coupling on the electronic spectra of the bilayer cuprates within the framework of a bilayer tight binding Hubbard Hamiltonian. Based on bilayer electronic band structure calculations Chakravarty and collaborators [11] have estimated a highly anisotropic intra cell coupling having the planar momentum dependence of the form
 which gives maximum bilayer splitting at
which gives maximum bilayer splitting at 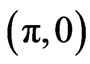 point of the Brillouin zone.
point of the Brillouin zone.
The influence of third dimension on the photoemission spectra of two dimensional materials has also been pointed out recently. Bansil et al. [12] have analyzed the intercell coupling on the basis of simulated ARPES lineshapes in Bi-2212 and concluded that the inter cell hopping induces a broadening to the photoemission spectra which have a characteristic dependence on the momentum . Markiewicz et al. [13] have also analyzed the effect of intercell coupling and the resulting
. Markiewicz et al. [13] have also analyzed the effect of intercell coupling and the resulting  dispersion in the cuprates within the framework of the one-band tight binding (TB) model Hamiltonian. These authors have obtained various values of tight binding parameters by fitting to the first principles local density approximation (LDA) based band structures, and also with experimental Fermi surfaces obtained by ARPES experiments in optimally doped and overdoped single layer cuprates, La2-xSrxCuO4 and Nd2−xCexCuO4 and bilayer cuprate Bi-2212.
dispersion in the cuprates within the framework of the one-band tight binding (TB) model Hamiltonian. These authors have obtained various values of tight binding parameters by fitting to the first principles local density approximation (LDA) based band structures, and also with experimental Fermi surfaces obtained by ARPES experiments in optimally doped and overdoped single layer cuprates, La2-xSrxCuO4 and Nd2−xCexCuO4 and bilayer cuprate Bi-2212.
The out-of-plane coupling not only connects the Cu-O planes within the unit cell (intra unit cell) but also Cu-O planes of the adjacent unit cells (inter unit cell). In bilayer cuprates due to small separation (of the order of 3.2 Å) between two Cu-O planes within the unit cell, the intra unit cell coupling between two Cu-O bilayers results in the band splitting as observed in ARPES measurements. On the other hand, the inter unit cell coupling that connects the two adjacent Cu-O planes in different unit cells is believed to be weaker due to greater separation (of the order of 12 Å in Bi-2212 cuprates) between Cu-O planes of two adjacent unit cells. Because of very low strength of inter unit cell interaction between Cu-O planes, their effect shows up only in recent high resolution ARPES measurements of Chuang et al. [5,14] on Bi-2212 system.
Several mechanisms have been proposed so far to explain the out of plane (c-axis) electronic conduction in multilayer cuprates [15,16] and we are still far from a clear understanding of c-axis electronic conduction in cuprates.
Recently, the influence of inter unit cell resonant tunneling between the copper-oxygen planes on c-axis electronic conductivity in normal state of optimally doped bilayer cuprates is investigated [17]. It is concluded that the c-axis conductivity increases with the increment in intercell resonant tunneling and this effect becomes more prominence at low temperatures (T < 300° K). Therefore, the resonant tunneling mechanism is able to account for out of plan (c-axis) electronic conduction processes in systems like Y-123 and Bi-2212. Most of the recent theoretical studies related to ARPES electronic spectra are based on the two dimensional tight binding Hubbard model and its extension within numerical and analytical approaches and the role of third dimensional coupling on the spectra in the presence of electrons correlation effect has not been clearly understood so far. Therefore, it would be interesting to study the effect of intra cell coupling, inter unit cell resonant tunneling, and electronic correlations simultaneously on the spectral function in doped multilayer cuprates in normal state.
2. Theoretical Formulation
For the system like Bi-2212 and Y-123 which have two Cu-O planes per unit cell, we have proposed a model Hamiltonian that incorporates the intra cell coupling, inter cell resonant tunneling alongwith strong Coulomb interaction that exist in cuprates.
The mechanism of inter unit cell resonant tunneling is schematically depicted in Figure 1 for Bi-2212 and Y-123 systems. The model Hamiltonian for cuprates with two Cu-O planes per unit cell which incorporates inter cell resonant tunneling is given below: (Equations 1(a) and (b))
where, m is unit cell indice and r, s are layer indices within a unit cell (where r = 1, s = 2 and vice-versa).  are creation (annihilation) operator for the holes of mth unit cell, rth Cu-O plane with wave vector k and spin
are creation (annihilation) operator for the holes of mth unit cell, rth Cu-O plane with wave vector k and spin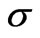 .The 1st term in 1(a) is kinetic energy of charge carrier (holes) within the Cu-O plane. The in plane band dispersion
.The 1st term in 1(a) is kinetic energy of charge carrier (holes) within the Cu-O plane. The in plane band dispersion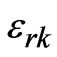 having the contribution of nearest neighbour hopping (t) and next nearest neighbour hopping (t') is taken as
having the contribution of nearest neighbour hopping (t) and next nearest neighbour hopping (t') is taken as
{ }
}
It also includes the chemical potential of coupled bilayer system and therefore, initially we have taken Fermi energy EF = 0 for our calculations. The 2nd term in 1 (a) is the on site Coulomb energy at Cu3d9 site and in cuprates this energy is quiet large (in the range 5 to 10 eV) as compared to hopping energy. The 3rd term in 1(a) is the single particle coupling between the bilayers within the unit cell and we have assumed momentum dependent of the form:

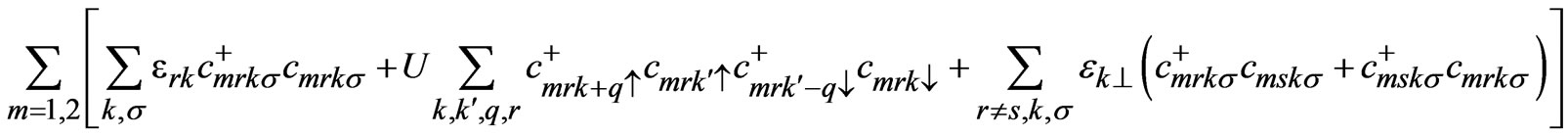 (1a)
(1a)
Hintercell =  (1b)
(1b)

Figure 1. Schematic presentation of intra cell coupling and inter unit cell resonant tunneling in bilayer cuprates (Bi-2212 and Y-123).
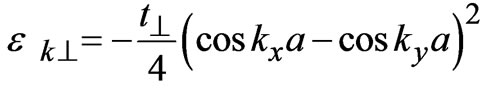
as suggested by band structure calculation [11] and ARPES measurements [3,4,12,13].
The 1st term in 1(b) represents the energy of the resonant level due to oxygen deficient BiO chain which lies mid way between the two Cu-O planes lying in adjoining unit cells. The 2nd term in 1(b) represents the single particle resonant tunneling from lower layer (say rth layer) of mth unit cell to upper layer (say sth layer) of adjacent (m + 1)th unit cell and vice-versa. The parameter Trs (m, m + 1) represent the inter unit cell resonant tunneling matrix element for the case when tunneling probability between two Cu-O planes in different unit cells is of the order of unity [18]. During the theoretical calculation Trs(m, m + 1) is taken as T12 for the case of nearest CuO planes in adjacent unit cells (Figure 1). To obtain an expression for the corresponding Green’s function
 and hence planar single particle spectral function A(k,
and hence planar single particle spectral function A(k, ) for the model Hamiltonian (1), we have employed Green’s function equations of motion approach [9,15,16]. Finally, we derived a set of coupled equations having higher order Green’s functions as:
) for the model Hamiltonian (1), we have employed Green’s function equations of motion approach [9,15,16]. Finally, we derived a set of coupled equations having higher order Green’s functions as:
 (2)
(2)
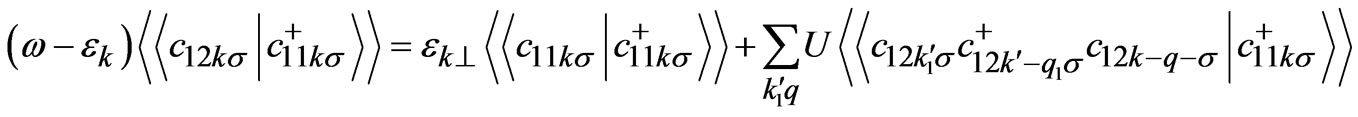 (3)
(3)
 (4)
(4)
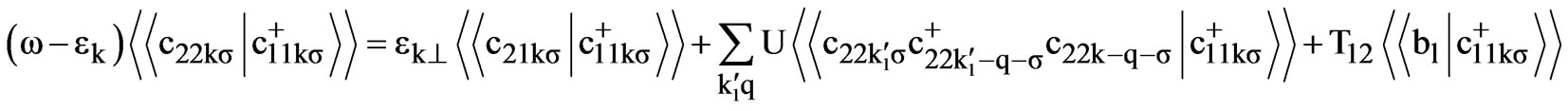 (5)
(5)
and
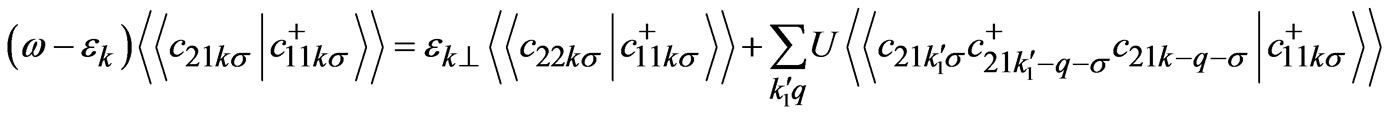 (6)
(6)
In order to take into account the electronic correlation effects that exist in cuprates, the equations of motion of higher order Green’s functions appearing in Equations (2)-(6) can be rewritten and the decoupling in higher order Green’s functions in these equations of motion is made at second stage. During the decoupling of higher order Green’s function, it is also assumed that the system is paramagnetic. This makes the equations tractable and avoids complications. With these approximations and simplification the higher order Green’s functions that exist in equations can now be written as:
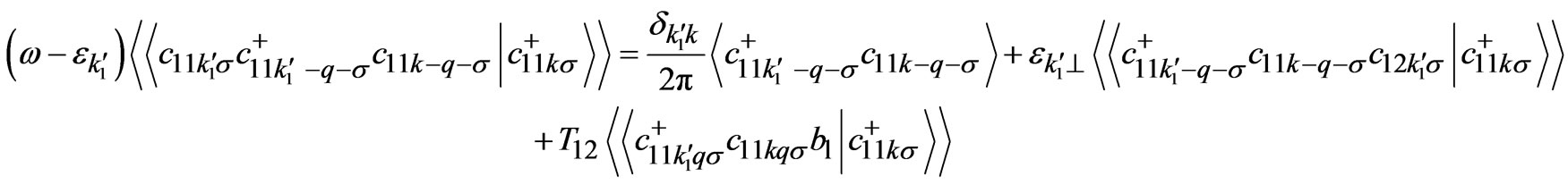
 (7)
(7)
The other higher order equations are also obtained and after truncating the hierarchy of still higher order Green’s function in the Hartree Fock approximation, we finally obtained set of linear coupled equations of Green’s functions. It is assumed that the charge carriers in Cu-O planes are equally distributed and also used a paramagnetic situation (i.e. carriers with up spin are equal to carriers with down spin). Solving the above coupled equations, one derives the Green’s function  as follows;
as follows;
 (8)
(8)
In the absence of Coulomb energy term (i.e. U = 0), the Equation (8), can be written in the following form.
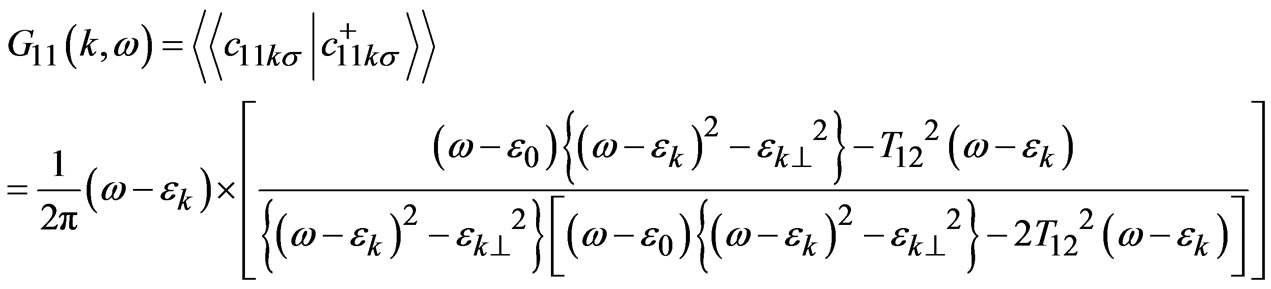 (9)
(9)
If, in the above expression of , the resonant tunneling is taken as zero (T12 = 0), we obtain the propagator for bilayer system having intra cell coupling only, and Equation (8) reduced to the following:
, the resonant tunneling is taken as zero (T12 = 0), we obtain the propagator for bilayer system having intra cell coupling only, and Equation (8) reduced to the following:
 (10)
(10)
One can check from above Equation (10) that there are two quasiparticle energy branches (i.e. ): a manifestation of intrabilayer coupling between two CuO2 planes within the unit cell. On simplification one can rewrite the Equation (8) as:
): a manifestation of intrabilayer coupling between two CuO2 planes within the unit cell. On simplification one can rewrite the Equation (8) as:
 (11)
(11)
whereA =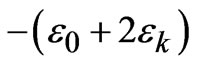
B =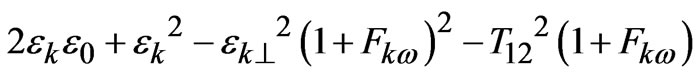
C =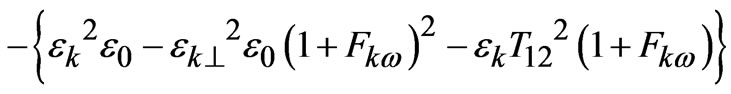
D =
E =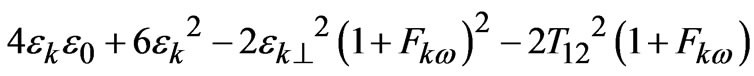
F =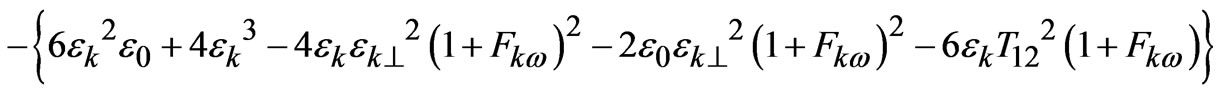
G =
and H = 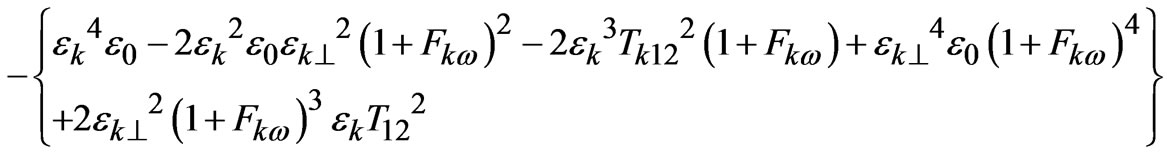
Using simple algebra above Equation (12) can be rearranged as:
 (12)
(12)
where,  are the five quasi-particle energies which have been computed numerically. The planar single particle spectral function A(k,
are the five quasi-particle energies which have been computed numerically. The planar single particle spectral function A(k, ) can be calculated from the above Green’s function
) can be calculated from the above Green’s function  numerically by using the relationship:
numerically by using the relationship:
A(k, )=
)= ,(13)
,(13)
where Im stands for imaginary part of Green’s function. Using Equations (12) and (13) the expression for planar electronic spectral function can be written in the following form:
A(k, )=
)= (14)
(14)
To fit the line shape of the photoemission experimental results, we need to solve  -functions involved in the spectral function (Equation (14)). The calculation of A(k,
-functions involved in the spectral function (Equation (14)). The calculation of A(k, ) would give a broadening of the quasiparticle peak. A Lorentizian type of broadening is used as given below:
) would give a broadening of the quasiparticle peak. A Lorentizian type of broadening is used as given below:
 (
( )
)
 (15)
(15)
The phenomenological broadening parameter  takes care of quasi-particle scattering rate and initially taken to be independent of k and
takes care of quasi-particle scattering rate and initially taken to be independent of k and  [19,20] as we are interested in the influence of inter unit cell resonant tunneling on photoemission spectral function. The line shape of the peak in the ARPES spectral function A(k,
[19,20] as we are interested in the influence of inter unit cell resonant tunneling on photoemission spectral function. The line shape of the peak in the ARPES spectral function A(k, ) can be analyzed using Equation (14) numerically.
) can be analyzed using Equation (14) numerically.
3. Results and Discussion
The spectral function  is measured by angle resolved photoemission spectroscopy. The measured
is measured by angle resolved photoemission spectroscopy. The measured  can be numerically analyzed using Equations (13-15). The
can be numerically analyzed using Equations (13-15). The  is analyzed especially at
is analyzed especially at 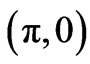 points of the Brillouin zone, where the splitting in the ARPES spectra of Bi2212 is found to be maximum in normal state. These calculations would be relevant to bilayer cuprates, Bi-2212, because the range of various intra and inter cell parameters used in the present analysis have been taken from recent electronic band structure calculations [10,11] and works on electronic spectra of Bi2212 cuprates [3,4,12,13].
points of the Brillouin zone, where the splitting in the ARPES spectra of Bi2212 is found to be maximum in normal state. These calculations would be relevant to bilayer cuprates, Bi-2212, because the range of various intra and inter cell parameters used in the present analysis have been taken from recent electronic band structure calculations [10,11] and works on electronic spectra of Bi2212 cuprates [3,4,12,13].
In Figure 2, one can observe the spectral function 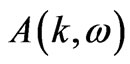 against energy
against energy  for different intra cell coupling strength in optimal doped regime of Bi-2212 in the normal state in the presence of inter cell resonant tunneling (T12 = 0.1 eV) and for the case U = 0.0 eV). The variation of
for different intra cell coupling strength in optimal doped regime of Bi-2212 in the normal state in the presence of inter cell resonant tunneling (T12 = 0.1 eV) and for the case U = 0.0 eV). The variation of  versus band energy
versus band energy  at
at  point of Brillouin zone shows a splitting in the spectral function in the presence of intra cell coupling between the planes (
point of Brillouin zone shows a splitting in the spectral function in the presence of intra cell coupling between the planes ( =0.2 eV). Such a bilayer splitting in Bi-2212 at
=0.2 eV). Such a bilayer splitting in Bi-2212 at  point is also observed in recent ARPES measurements [4-7]. On introducing the inter unit cell resonant tunneling (
point is also observed in recent ARPES measurements [4-7]. On introducing the inter unit cell resonant tunneling ( =0.05 eV, 0.075 eV and 0.1 eV and keeping
=0.05 eV, 0.075 eV and 0.1 eV and keeping  =0.1 eV), one can point out a broadening in the spectral function (Figure 3). Also, the bilayer splitting in the spectral function disappeared due to broadening in the spectra on increasing inter cell resonant tunneling term (T12 = 0.1 eV to 0.15 eV) (Figure 4). Such broadening in the normal state spectra has also been predicted by simulated ARPES line shapes in Bi-2212 bilayer systems as manifestation of third dimensional inter unit cell coupling [12,13]. On comparing Fig. 2 and Figure 4 one can observe that intra cell coupling (
=0.1 eV), one can point out a broadening in the spectral function (Figure 3). Also, the bilayer splitting in the spectral function disappeared due to broadening in the spectra on increasing inter cell resonant tunneling term (T12 = 0.1 eV to 0.15 eV) (Figure 4). Such broadening in the normal state spectra has also been predicted by simulated ARPES line shapes in Bi-2212 bilayer systems as manifestation of third dimensional inter unit cell coupling [12,13]. On comparing Fig. 2 and Figure 4 one can observe that intra cell coupling ( ) leads the bilayer splitting in the spectral function, while inter unit cell resonant tunneling (T12) suppresses the bilayer splitting and induces broadening in the spectral peak close to Fermi level.
) leads the bilayer splitting in the spectral function, while inter unit cell resonant tunneling (T12) suppresses the bilayer splitting and induces broadening in the spectral peak close to Fermi level.
One can also analyze the influence of inter cell resonant tunneling term (T12) on the spectral function at
 point in the presence of Coulomb correlation (U), keeping other parameters fixed, and using Green’s func-
point in the presence of Coulomb correlation (U), keeping other parameters fixed, and using Green’s func-
tion Equation (18). In Figure 5, the spectral function versus energy for different values of inter cell resonant tunneling term (T12 = 0.1 eV to 0.25 eV) in the presence of Coulomb correlation (i.e. U = 3 eV) have been plotted. It is pointed out from the Figure 5 that in the presence of both the electronic correlations, and inter cell resonant tunneling (T12) the broadening in spectra [1-4] is more as compare to the absence of Coulomb correlations (Figures 3 and 4).
Finally, it is concluded that the intra unit cell coupling is responsible for bilayer splitting of electronic spectra, while the inter unit cell resonant tunneling leads to broadening in the spectral features especially at  point of optimally doped bilayer (Bi-2212) cuprates and in good correspondence with recent ARPES measurements [12]. The electron correlations also play an important role in determining the shape of spectral function. As the antinodal region of hole doped cuprates is so called hot spot, in which the electron-electron correlation broaden the spectral function. Besides, there may be another source to broaden the spectral function like as randomness in the CuO2 planes alongwith inter cell incoherent resonant tunneling and carrier concentration. Therefore, the presence of finite electron correlations, the inter unit cell resonant tunneling (T12) suppresses the bilayer splitting in the spectral function due to broadening in the spectral features close to Fermi level in optimal doped bilayer cuprates.
point of optimally doped bilayer (Bi-2212) cuprates and in good correspondence with recent ARPES measurements [12]. The electron correlations also play an important role in determining the shape of spectral function. As the antinodal region of hole doped cuprates is so called hot spot, in which the electron-electron correlation broaden the spectral function. Besides, there may be another source to broaden the spectral function like as randomness in the CuO2 planes alongwith inter cell incoherent resonant tunneling and carrier concentration. Therefore, the presence of finite electron correlations, the inter unit cell resonant tunneling (T12) suppresses the bilayer splitting in the spectral function due to broadening in the spectral features close to Fermi level in optimal doped bilayer cuprates.
4. Acknowledgements
We are highly thankful to Prof. S. K. Joshi, National Physical Laboratory, New Delhi, India for his valuable suggestions and encouragement.