Channel Error Estimation Methods Comparison under Different Conditions for Multichannel HRWS SAR Systems ()

1. Introduction
Conventional SAR system suffers from the limitation of achieving high resolution and wide swath (HRWS) simultaneously [1]-[10]. Multichannel in azimuth HRWS SAR, combined with digital beam forming (DBF) technique [2] [7], can effectively deal with this problem. Channel mismatch, caused by central electronic equipment, antenna array and satellite platform, and so on, will seriously affect the image quality in multichannel SAR systems. So channel error estimation and compensation becomes very crucial [2].
This paper mainly deals with the problem of channel errors in multi-channel HRWS SAR systems. In recent years many algorithms have been put forward to estimate the channel errors. The four main methods are time- domain correlation method (TDCM) [3], orthogonal subspace method (OSM) [4], signal subspace comparison method (SSCM) [5] [6] and antenna pattern method (APM) [5] [6]. Some simple comparisons of these methods have also been done [5] [6]. However, the performances of the estimation methods have only been compared under the Gaussian clutter scenes without theoretical analysis. In this paper, comprehensive comparison is done under different SNR conditions and different clutter distributions. In addition, theoretical analysis is given to explain the differences. The results and analysis will provide evidence for method selection in real engineering applications.
2. Echo Model
The geometric model of an actual multi-channel SAR system is shown in Figure 1.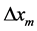 ,
, 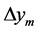 and
and 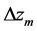 denote the antenna position measurement error along X, Y, and Z axis, respectively.
denote the antenna position measurement error along X, Y, and Z axis, respectively.
Taking the channel errors caused by several factors into account [2], the total magnitude error and phase error of the mth channel can be denoted as 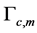 and
and . Echo of the mth channel can be expressed as:
. Echo of the mth channel can be expressed as:
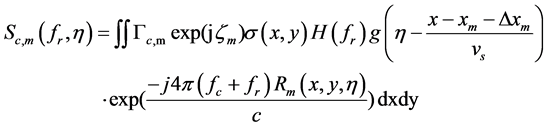 , (1)
, (1)
where
 . (2)
. (2)
3. Error Estimation Methods
Since channel magnitude errors can be estimated and compensated by simple channel balancing [5], this paper mainly concerns channel phase error estimation methods.
3.1. Time-Domain Correlation Method (TDCM)
The TDCM is presented in [3]. This estimation algorithm is operated in time-domain. Firstly, the echoes received by adjacent channels are multiplied in time-domain to get the interferometry
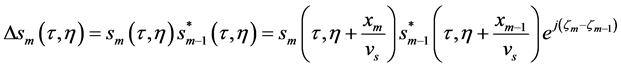 , (3)
, (3)
where  is the echo of the mth channel, and
is the echo of the mth channel, and 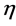 denoted the slow-time.
denoted the slow-time.
From the principle of the average cross correlation method in the baseband Doppler centroid estimation, there is
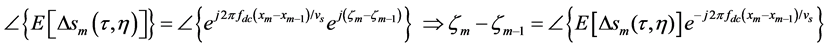 , (4)
, (4)
![]()
Figure 1. Geomentry of a multichannel SAR system.
where  is the Doppler centroid.
is the Doppler centroid.
Assume that the first channel is the reference channel, phase error of the mth channel is
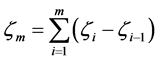 . (5)
. (5)
3.2. Orthogonal Subspace Method (OSM)
The OSM is presented in [4]. This algorithm utilizes the orthogonality between the signal subspace and noise subspaces after eigenvalue decomposition, which is processed in Doppler domain.
Channel phase errors are estimated by minimize the cost function:
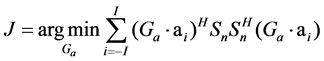 , (6)
, (6)
where 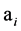 is the array steering vector, and
is the array steering vector, and 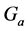 is a square matrix whose diagonal elements are phase errors in exponential form. Sn corresponds to the noise subspace, whose column vectors are noise eigenvectors.
is a square matrix whose diagonal elements are phase errors in exponential form. Sn corresponds to the noise subspace, whose column vectors are noise eigenvectors.
Let the first channel be the reference channel, and denote![]() . The estimation of phase errors can be expressed as
. The estimation of phase errors can be expressed as
![]() , (7)
, (7)
where.![]() (8)
(8)
3.3. Signal Subspace Comparison Method (SSCM)
The SSCM is expressed in [5]. This algorithm makes use of the fact that the space spanned by the signal subspace eigenvectors is the same as the space spanned by the array steering vector
![]() . (9)
. (9)
Let ![]() (10)
(10)
According to the uniqueness of orthogonal projection operator, we can get
![]() . (11)
. (11)
Let![]() ,
, ![]() , then
, then
![]() . (12)
. (12)
3.4. Antenna Pattern Method (APM)
The APM is expressed in [6]. This algorithm estimates the channel phase errors by combining with the antenna pattern.
Let![]() . Ignoring the effect of noise, from the first column of the correlation matrix, there is
. Ignoring the effect of noise, from the first column of the correlation matrix, there is
![]() . (13)
. (13)
Then the relative phase error of the mth channel can be expressed by
![]() . (14)
. (14)
4. Performance Comparison and Analysis
In this section, experiment is done to compare the performance of the above mentioned four algorithms. The parameters are listed in Table 1, where M is the number of channels, ![]() is the antenna size in azimuth,
is the antenna size in azimuth, ![]() is the wavelength, PRFM is the pulse repetition frequency, and
is the wavelength, PRFM is the pulse repetition frequency, and ![]() is the velocity of platform. Figure 2 shows a brief illustration of transmitting and receiving of the SAR system.
is the velocity of platform. Figure 2 shows a brief illustration of transmitting and receiving of the SAR system.
To compare the four methods discussed above, we use two indexes: estimation deviation and the maximum azimuth ambiguity-to-signal ratio (AASRMAX). Estimation deviation means the bias between the real phase error and the estimated phase error. AASRK is the ratio of power of kth (k = 1 - 8) ambiguity component to power of the ambiguity free signal after phase error estimation and compensation [3], i.e.
![]() . (15)
. (15)
Besides, AASRMAX is the maximum of AASRK (k = 1 - 8).
4.1. Estimation Performance Versus SNR
In this section, clutters are assumed to be Gaussian distribution, and SNR varies from 0 dB to 20 dB. The estimation deviations of eight channels are illustrated in Figure 3. The maximum estimation deviations and AASRMAX are listed in Table 2 for different SNR.
4.2. Performance Comparison under Different Clutter Distributions
In engineering application, clutter scenario does not obeyideal Gaussian distribution. Log-normal distribution, Weibull distribution and K-distribution are mainly considered as sea clutter model when HRWS SAR detects the seasurface.
This section mainly compares the performance of the four algorithms when clutter obeys Log-normal distribution, Weibull distribution and K-distribution, respectively. The estimation deviations of eight channels under SNR = 0 dB are illustrated in Figure 4. The maximum estimation deviations and AASRMAX for different clutter distributions and different SNR are listed in Table 3 and Table 4, respectively.
4.3. Analysis of the Results
Without eigenvalue decomposition and matrix inversion, the computational load of TDCM is the lowest. However, TDCM works worse than the other three algorithms under all simulated clutter distributions and SNR, for the deviation is cumulative when the phase error accumulates.
APM also does not need eigenvalue decomposition and matrix inversion, which is characterized by light computational load. But this method only applies to uniform distribution scenes. When the clutter obeys Weibull distribution and K-distribution, it works worse than OSM and SSCM under low SNR conditions (0 - 10 dB). While under high SNR conditions (>10 dB), the differences of APM, OSM, and SSCM are very small. The frequency spectrums of Weibull distribution and K-distribution are not quite homogeneous, so the performance of APM deteriorates when the noise is relatively large. For Gaussian distribution and Log-normal distribution clutters, the scenarios are homogeneous, so APM works as well as OSM and SSCM.
![]()
Figure 2. Illustration of transmitting and receiving of eight-channel SAR system.
![]()
Table 1. Parameters of multi-channel SAR system.
![]()
Table 2. Maximum estimation deviations and AASRMAX for four algorithms.
![]()
Table 3. Maximum estimation deviations for four algorithms under three clutter distributions.
![]()
Table 4. AASRMAX for four algorithms under three clutter distributions.
The OSM and SSCM use the signal subspace and noise subspaces after eigenvalue decomposition of the correlation matrix, respectively. Assuming L Doppler bins are used to estimate the phase errors, the computational load of OSM and SSCM are 2 LM3 and LM3 + M3, respectively. Their performances are best under all simulated clutter distribution and SNR conditions.
In application, when the scenes are homogeneous, such as agricultural and natural areas, APM can be chosen to estimate the channel phase errors for its accuracy and light computational load. In contrast, for heterogeneous scenes such as urban or sea surfaces, OSM and SSCM are suitable for phase error estimation.
![]()
![]() (a) (b)
(a) (b)
Figure 3. Estimation deviations of eight channels versus SNR for the time-domain correlation method (dashed red), the orthogonal subspace method (dashed green), the signal subspace comparison method (dashed black), the antenna pattern method (dashed blue). SNR = 0 dB corresponds to Figure 3(a), and SNR = 10 dB corresponds to Figure 3(b).
![]() (a)
(a)![]()
![]() (b) (c)
(b) (c)
Figure 4. Estimation deviations of eight channels under SNR = 0 dB. Log-normal distribution clutter corresponds to Figure 4(a), Weibull distribution clutter corresponds to Figure 4(b), and K-distribution clutter corresponds to Figure 4(c).
5. Conclusion
In this paper, four channel error estimation methods for multichannel HRWS SAR system are compared under different SNR conditions and clutter distributions. From the simulation results, we can conclude that the estimation deviations are not relevant to real phase error distribution, and only relate to SNR and the clutter distribution. In addition, the performance of time-domain correlation method is poorer than the other three methods. For Doppler-domain methods, the APM works as well as the OSM and SSCM for homogeneous clutter scenes, but worse than OSM and SSCM for heterogeneous surfaces. OSM and SSCM work best for all clutter scenes.