Some Factors Influencing the Dielectric Properties of Natural Rubber Composites Containing Different Carbon Nanostructures ()
Received 14 January 2016; accepted 26 February 2016; published 29 February 2016

1. Introduction
A growing number of demanding applications in electronics and telecommunications rely on the unique properties of carbon allotropes. The need for microwave absorbers and radar-absorbing materials is steadily increasing in military applications (reduction of radar signature of aircraft, ships, tanks, and targets) as well as in civilian applications (reduction of electromagnetic interference (EMI) among components and circuits, reduction of the back-radiation of microstrip radiators [1] ).
In recent times researchers have tried three types of carbonaceous fillers, i.e., carbon black (CB), carbon fiber (CF) and carbon nanotubes including multiwalled (CNTs/MWNTs) [2] with a suitable polymer matrix. In certain cases, pairs of fillers have been tried. The different structures and shapes of these conductive fillers and the morphologies of their dispersion will affect the ability to construct an effective conductive network, which is key to increasing the electrical conductivity of the polymer-filler composites [3] [4] . Some researchers [5] [6] have simultaneously introduced CB and CNTs into polymer matrices through conventional processing techniques.
A composite absorber that uses carbonaceous particles in combination with a polymer matrix offers a large flexibility for design and properties control, as the composite can be tuned and optimized via changes in both the carbonaceous inclusions (carbon black, carbon nanotube, carbon fiber, graphene) and the embedding matrix (rubber, thermoplastic) [1] [7] - [9] .
Polymer composites containing conductive fillers have been developed in recent times as alternative EMI shielding materials since they possess the advantages like light weight, low cost, resistant to corrosion and processing advantages. However, in such materials, the EMI shielding effectiveness depends on many factors, including filler’s intrinsic conductivity, filler loading, dielectric constant, aspect ratio and filler-polymer matrix interactions [10] .
Dielectric properties of materials are those electrical characteristics of poorly conducting materials that determine their interaction with electric fields. Those properties determine how well energy from the high-frequ- ency alternating electric fields can be absorbed and thus how rapidly the materials will be heated. The dielectric properties of the load materials are also important in the design of the radio frequency or microwave power equipment [11] [12] .
The complex permittivity relative to free space may be represented as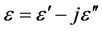 , where
, where 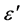 is the dielectric permittivity (dielectric constant) and
is the dielectric permittivity (dielectric constant) and 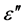 is the dielectric loss factor. The real part of the permittivity represents the energy storage capability in the electric field in the dielectric material, and the imaginary part represents the energy dissipation capability of the dielectric by which energy from the electric field is converted into heat energy in the dielectric. Often, the loss angle of dielectrics is of interest, and the tangent of the loss angle δ is used (tan
is the dielectric loss factor. The real part of the permittivity represents the energy storage capability in the electric field in the dielectric material, and the imaginary part represents the energy dissipation capability of the dielectric by which energy from the electric field is converted into heat energy in the dielectric. Often, the loss angle of dielectrics is of interest, and the tangent of the loss angle δ is used (tan ) [13] [14] .
) [13] [14] .
In principle, the dielectric properties of most materials vary with several influencing factors. The dielectric properties depend on the frequency of the applied alternating electric field, the temperature and the water content of the material, its density, etc. The dielectric properties are dependent also on the presence of mobile ions and the permanent dipole moments. The distribution of the phases, including voids and cracks, has also a major influence on the dielectric properties of the composite materials [12] [15] .
Among the fillers used in the last years, carbon-based nanostructures, such as fullerenes (Fs), carbon nanotubes (CNTs) and graphene nanoplatelets (GNPs) have been studied extensively. The reason for the interest in the above mentioned carbon nanostructures and their application in rubber composites can be explained with their unique properties (Table 1).
These materials have different aspect ratios and specific surface areas, and structures: CNTs are known to have high aspect ratio (several hundred to thousand), outstanding electrical and mechanical properties [19] - [21] . Also, GNPs are comprised of short stacks of platelet-shaped graphene sheets that are identical to those found in the walls of CNT, but in a planar form. GNPs can increase considerably the thermal conductivity and stability, and barrier properties [22] [23] . The fullerenes have a cage-like structure. Their major difference, compared to classical modification of carbon, is the molecule being a more or less punctiform, discrete unit instead of a structure repeating dimensionally through space [24] . It is obvious, that as Fs, CNTs, and GNPs have different characteristics, different geometries, aspect ratios, crystallography structure and physical properties, so their effects on the properties of polymer nanocomposites should be different, as shown in [25] - [28] .
It is often difficult to explain most of the complex dielectric properties in the disordered composites [29] . Theoretical predictions of the fundamental physical data suffer from a lack of experimental data, especially dielectric data over a wide frequency range. We therefore conducted high resolution measurements of frequency-dependent dielectric properties in the carbonaceous fillers /natural rubber composites.
![]()
Table 1. Characteristics of some carbon nanostructures [16] - [18] .
The aim of this work is to prepare natural rubber based composites containing different amounts (2 - 10 phr) (phr = parts of filler by weight per hundred parts of rubber) of fullerenes, CNTs and GNPs; to analyze the role of some factors and specific structure features of these fillers on the microwave dielectric behavior of the composites with a view to propose lightweight, flexible materials suitable for microwave absorbers in wide frequency range (1 - 12 GHz).
2. Experimental
2.1. Materials
Natural rubber SMR 10 (Moony viscosity, ML1+4 at 100˚C = 60; dielectric constant ε = 2.1) was purchased from North Special Rubber Corporation of Hengshui, Hebei Province, China.
Other ingredients such as zinc oxide (ZnO), stearic acid (SA), N-tert-Butyl-2-benzothiazolesulfenamide (TBBS) and sulphur (S) were commercial grade and used without further purification.
2.2. Characterization of the Fullerene Used
The investigations reported in this paper were on neat fullerene powder comprising 99.5% of С60 fullerene produced by Alfa Aesar (Johnson Matthey Company). Fullerene density was 1.65 g/cm3. The micrograph in Figure 1(a) and the 50 nm marker on it show the fullerene particles to be aggregates of several hundred nm in size, e.g. 300 nm wide and 700 nm long, composed of initial particles about 50 - 60 nm large. The insert in Figure 1(a) is a micrograph taken in an electron diffraction regime of the aggregate which shows its having a crystal structure as the initial fullerene particles do.
2.3. Characterization of the Carbon Nanotubes Used
Multiwalled carbon nanotubes produced by Grafen Chemical Industries Co., Ankara, Turkey, were used in our investigation. The material’s purity was more than 95%, density −2.6 g/сm3. Carbon nanotubes were with average diameter about 15 nm and length 1 - 10 microns. Figure 1(b) shows the micrograph of the aggregate and the pattern taken in an electron diffraction regime showing that it has a crystal structure such as the primary CNTs particles have.
2.4. Characterization of the Graphene Used
Graphene used in the investigation was also produced by Grafen Chemical Industries Co., Ankara, Turkey. Graphene nanoplatelets (GNP) have a “platelet” morphology, meaning they have a very thin but wide aspect. Aspect ratios for this material can range into the thousands. Each particle consisted of several sheets of graphene with an overall thickness of 50 nm and average plate diameter 40 micron (Figure 1(c)), the density was 0.4 g/cm3.
2.5. Preparation of Rubber Composites
Table 2 summarizes the formulation characteristics of the rubber compounds (in phr) used in the investigations.
The rubber compounds were prepared according to a specific recipe. The pre-characterized filler powder was incorporated into the natural rubber matrix at various loadings on an open two-roll laboratory mill (L/D 320 × 360 and friction 1.27). The speed of the slow roll was 25 min−1. The formulations of the compounds prepared are shown in Table 2. The compounding was carried out as follows: the raw rubber was loaded into the mill;
![]()
Table 2. Compositions of rubber compounds (in phr).
aMercaptobenzothiazole sulphenamide; bTetramethylthiuram disulphide; cDimethyl butyl- phenyl-p-phenylendiamine.
![]()
![]()
![]() (a) (b) (c)
(a) (b) (c)
Figure 1. Micrographs of fullerene aggregates (a); CNT aggregates (b) and GNPs aggregates (c) in transmission regime and in selected area electron diffraction regime (inserts).
ZnO and stearic acid were added after 5 min. After 3 min of homogenization the filler was added. Following another homogenization for 7 min the accelerator and sulphur were added and the compound was rehomogenized for 4 min. The temperature of the rolls did not exceed 70˚C. The experiments were repeated for verifying the statistical significance. The ready compounds in the form of sheets stayed 24 hours prior to their vulcanization. The optimal vulcanization time was determined by the vulcanization isotherms taken on an oscillating disc vulcameter MDR 2000 (Alpha Technologies) at 150˚C, according to ISO 3417:2002. The vulcanization was performed on an electric hydraulic press which plate was 400 × 400 mm, at 10 МРа.
The properties of the composites obtained―dielectric constant and dielectric loss―were determined in the 1 - 12 GHz frequency range.
2.6. Measurements
2.6.1. Complex Permittivity
The determination of complex permittivity was carried out by the resonance method, based on the cavity perturbation technique [30] . The resonance frequency of an empty cavity resonator fr was measured. After that the sample material was placed into the resonator and the shift in resonance frequency fε was registered. The real part of permittivity  (dielectric constant) was calculated from the shift in resonance frequency, cavity and the sample cross sections, Sr and Sε, respectively:
(dielectric constant) was calculated from the shift in resonance frequency, cavity and the sample cross sections, Sr and Sε, respectively:
 (1)
(1)
The sample was in the form of a disc with a diameter of 11 mm and about 1.5 mm thick. Its location in the cavity was at the maximum electric field. Because the thickness of the sample was not equal to the height of the resonator, a dielectric occurred with an equivalent permittivity εe at the place of its inclusion. The parameter was determined by Equation (1) and instead  was saved εe. Then
was saved εe. Then 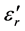 was determined by
was determined by
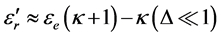 (2)
(2)
where k = l/Δ and l is the distance from the disk to the top of the resonator.
2.6.2. Loss Factor tanδ
The loss factor tan δ was calculated from the quality factor of the cavity [31]
 (3)
(3)
where Qε―quality factor of the cavity with a sample and Qr―quality factor of the cavity without a sample.
The measurement setup used several generators for the whole range: HP686A and G4-79 to 82, frequency meters: H 532A; FS-54, a cavity resonator. The scheme of the equipment used is shown on Figure 2.
The dielectric properties were measured in the frequency range from 1 GHz to 12 GHz.
3. Results and Discussion
3.1. Dielectric Properties Frequency Dependence
The frequency dependence of the dielectric permittivity of NR based composites, containing a different amount of fullerenes, CNTs and GNPs is shown in Figures 3-5. It is evident that the dielectric permittivity values increase with the increasing frequency in the case of any of the fillers used. In the 1 - 7 GHz range the increase is slightly pronounced while in the 7 - 12 GHz range it is more drastic. The specifics of the fillers used are expressed in the slope of plotted curves.
Figures 6-8 present the dielectric loss in the 1 - 12 GHz frequency range of the composites investigated. The changes in the imaginary part of the relative complex permittivity of the material also known as dielectric loss angle tangent―tan δε―depend on the frequency. As expected, with the increasing frequency the dielectric loss decreases, more rapidly in the region 5 - 12 GHz. Evidently, when GNPs are used as filler, the frequency increase has a stronger effect on the dielectric losses of the samples at lower frequencies (1 - 4 GHz). Noteworthy is the fact that in the 11 - 12 GHz frequency range the values of dielectric losses of the samples examined become closer.
The results in Figures 3-8 allow the conclusion that the dielectric properties of most materials vary considerably with the frequency of the applied electromagnetic field. An important phenomenon contributing to the frequency dependence of the dielectric properties is the polarization, arising from the orientation of molecules which have permanent dipole moments with the imposed electric field. The mathematical formulation developed by Debye to describe the permittivity for polar materials [32] can be expressed as
![]()
Figure 2. Scheme of the equipment for measuring the dielectric properties.
![]()
Figure 3. Frequency dependence of dielectric permittivity ![]() at a various filler content (n-phr of fullerenes).
at a various filler content (n-phr of fullerenes).
![]()
Figure 4. Frequency dependence of dielectric permittivity ![]() at a various filler content (n-phr of CNTs).
at a various filler content (n-phr of CNTs).
![]()
Figure 5. Frequency dependence of dielectric permittivity ![]() at a various filler content (n-phr of GNPs).
at a various filler content (n-phr of GNPs).
![]()
Figure 6. Frequency dependence of dielectric loss tanδ at a various filler content (n-phr of fullerenes).
![]()
Figure 7. Frequency dependence of dielectric loss tanδ at a various filler content (n-phr of CNTs).
![]()
Figure 8. Frequency dependence of dielectric loss tanδ at a various filler content (n-phr of GNPs).
![]() (4)
(4)
where ω = 2πƒ is the angular frequency, ε∞ represents the dielectric constant at frequencies so high that molecular orientation does not have time to contribute to the polarization, εs represents the static dielectric constant, i.e., the value at zero frequency (dc value), and τ is the relaxation time in seconds, the period associated with the time for the dipoles to revert to random orientation when the electric field is removed. Separation of Equation (4) into its real and imaginary parts yields
![]() (5)
(5)
![]() (6)
(6)
Obviously, ε∞, εs and in particular, τ are specific parameters for each of the fillers used, which depend on the fillers chemical and crystallographic nature. Therefore, the dielectric properties of the composites studied depend differently on the frequency, provided all other conditions are identical (the same polymer matrix and filling degree). The dependence of ε∞, εs and τ on the fillers chemical nature and structure explains why in some frequency range (usually at lower frequencies) the dielectric properties change monotonously, while in some higher frequency range, when relaxation is hindered, the increase is drastic. According to the Debye theory of dielectric properties [31] , ![]() is generally determined by relaxation and electrical conductivity losses. It is clear that both polarization relaxation and electrical conductance can affect
is generally determined by relaxation and electrical conductivity losses. It is clear that both polarization relaxation and electrical conductance can affect![]() .
.
The Debye relaxation is one of the important dielectric loss mechanisms, which can be characterized by ![]() -
- ![]() relationship. Figure 9 presents the dependence of the dielectric loss
relationship. Figure 9 presents the dependence of the dielectric loss ![]() on dielectric permittivity
on dielectric permittivity ![]() for the NR based composites comprising different carbon nanostructures. As seen from this figure, for each of the fillers the dependence is strictly specific and differing from the rest. For instance, in the case of composites filled with GNPs the dielectric loss remains practically the same in a quite large interval of dielectric permittivity values (from 2.5 to 5.5). Moreover, there are regions of almost linear decrease of the dielectric loss with the increasing dielectric permittivity values for those composites. The dependence curve for the composites comprising
for the NR based composites comprising different carbon nanostructures. As seen from this figure, for each of the fillers the dependence is strictly specific and differing from the rest. For instance, in the case of composites filled with GNPs the dielectric loss remains practically the same in a quite large interval of dielectric permittivity values (from 2.5 to 5.5). Moreover, there are regions of almost linear decrease of the dielectric loss with the increasing dielectric permittivity values for those composites. The dependence curve for the composites comprising
![]()
Figure 9. Dependence of dielectric loss on the dielectric permittivity values for composites filled with nanostructures of different chemical nature at 10 phr, studied in 1 - 12 GHz frequency range.
fullerenes has an S-shaped pattern with two regions wherein the dielectric loss values decrease almost linearly with the increasing dielectric permittivity, in the third region of curve that decrease is intermittent. As Figure 9 shows, the relaxation proceeds in a different manner. For each of the studied fillers the real and imaginary parts of the complex dielectric permittivity change at different intervals. As all other conditions are identical, obviously, that peculiarity is due to the specific chemical nature and crystallographic structure of the fillers.
On the other hand, since the elastomer matrix is non-polar, apparently, the relaxation and polarization processes are greatly dependent on the fillers used and on their specific features. With regard to those specifics, the polarization may proceed according to three different mechanisms: electronic, ionic and orientational. All non-conducting materials are capable of electronic polarization. Therefore, we consider the polarization of the elastomer matrix used for the studied composites to proceed according to that mechanism. The ionic and orientational polarizations occur only in materials possessing ions and permanent dipoles, respectively. It might be assumed that the matrix and the fillers introduced into it polarize according to a different mechanism. The more polarization mechanisms of a composite are, the higher its dielectric constant will be. For example, a natural rubber based composite containing fillers with permanent dipoles have a dielectric permittivity higher than the one of non polar natural rubber. On the other hand, the more easily the various polarization mechanisms can act, the higher the dielectric permittivity will be. For example, among elastomers, the more mobile the chains are (i.e. the lower the degree of crystallinity), the higher the dielectric permittivity will be. It is important for the composites investigated, because the natural rubber crystallizes and the chemical nature of the fillers used and their amounts can change the degree of crystallinity and the dielectric permittivity. For polar structures the magnitude of the dipole also affects the magnitude of the occurring polarization. The fillers with non-centrosymmetric structure have especially strong spontaneous polarization, hence a high dielectric permittivity, respectively.
3.2. Dielectric Properties Filler Concentration Dependence
It is obvious from Figures 3-8 that, in the investigated concentration interval, the values of the dielectric permittivity are too close to each other with a tendency to a slight increase with the increasing filler concentration. A similar tendency has been described by the authors [28] who have investigated the change in the dielectric permittivity of natural rubber based composites filled with fullerenes in the concentration interval from 0.065 to 0.75 phr. They have found an increase in those values from 4.8 to 5.2, respectively, with the increasing concentration; however, that investigation refers to a frequency of only 50 Hz.
When CNTs are used as fillers (Figure 4) the dielectric permittivity values are relatively close at lower frequencies (up to 7 GHz). At frequencies higher than 7 GHz the dielectric permittivity increases with the increasing filler concentration.
Of particular interest is the 9 - 12 GHz range wherein there is a relatively fast increase in the dielectric permittivity and its dependence on the amount of GNPs is the most prominent.
From the very beginning of that range the values of tanδ are clearly distinguished as dependent on the different degree of filling. As expected, the increase in filler amount leads to an increase in tanδε values (Figures 6-8).
The imaginary part of the complex relative permittivity is more sensitive to changes in the filler amount than the real part is.
3.3. Dielectric Properties Physical Structure and Chemical Nature Dependence
Carbon nanofillers used have different geometries and exhibit different surface area/volume relations [24] . Some of their specific features are shown in Table 1.
The investigations carried out and the obtained results (Figures 3-9) show irrevocably the impact that the crystallographic structure and the chemical nature of the used fillers have upon the dielectric permittivity values and dielectric loss. The effect could be explained first of all by the polarization and by the mechanism according to which the polarization proceeds, as well as by the proceeding of relaxation and the time needed for the process. The aforementioned two processes are crucial for the dielectric properties of the materials when applying an electromagnetic field. The difference in the crystallographic structure and chemical nature of the fillers predetermine the differences in the dielectric permittivity values and dielectric losses of composites based on the same matrix. The effects of the two factors (crystallographic structure and chemical nature) sometimes intermingle and are hardly distinguishable. That could be the scope of future investigations.
4. Conclusion
Natural rubber (NR) based composites containing different carbon nanofillers (fullerenes, carbon nanotubes and graphene nanoplatelets) at concentrations from 2 to 10 phr have been prepared. Their dielectric properties (dielectric permittivity, dielectric loss) have been studied in the 1 - 12 GHz frequency range. It was found that the dielectric constant and dielectric loss of filled composites depend on amount and type of filler loading. It has been established that with increasing the frequency of the electromagnetic field the dielectric permittivity values increase, while those of the dielectric losses get lower. The higher the concentration of the fillers is (keeping identical all other conditions), the higher the values of dielectric permittivity and dielectric losses are. The observed effects are related first of all to the impact that the chemical nature and crystallographic structure of the fillers and elastomer matrix studied have upon the polarization time and mechanism as well as upon the relaxation time and mechanism. The latter processes determine the dielectric properties of the materials. The dielectric properties of the developed natural rubber composites containing conductive fillers (fullerenes, CNTs, GNPs) indicate that these composites can be used as broadband microwave absorbing materials.
Acknowledgements
The work is a part of a project funded by King Abdulaziz University, Saudi Arabia under grant number MB/11/12/436. The authors acknowledge the technical and financial support.
NOTES
![]()
*Corresponding author.