Characterization and Modeling of Large-Scale Fading for Radio Propagation in Rwanda ()
Received 24 October 2015; accepted 26 February 2016; published 29 February 2016

1. Introduction
The advanced accessibility and improved performance of radio links are needed for high quality signals transmission. According to [1] [2] , the knowledge of parameters that affect the propagation of radio waves between radio link terminals is required to predict the level of fluctuations that may occur in the amplitude of the received signal and its phase to design the highly reliable radio communication networks [3] . In narrowband systems, two types of fading can take place: large-scale fading and small-scale fading. The first is due to shadowing and is typically modeled by log-normal distribution. The latter is due to multipath propagation and is generally described by Rayleigh density function when signals are constituted by multiple radio path components for non- line-of-sight (NLOS) or by Rice density function when signals are formed by a line-of-sight (LOS) plus multiple radio path components. As wireless medium, troposphere affects the propagation of radio waves between radio link terminals [1] [2] .
In this work, we review the large scale fading models and their probability distributions; the other sections consist of a case study, results and discussions. The work ends with a conclusion.
2. Large-Scale Fading Models
The large-scale fading is characterized by average path loss and shadowing [4] . Large-scale wireless channel models illustrates the power-loss of signals in the case of a large distance between the transmitter and the receiver for a propagation environment which is not critically populated and this is the case for suburban areas; the large scale models contribute to the prediction of reflection, diffraction and long distance power loss [5] [6] .
1) Free-space path loss model
This model takes into account the propagation along line-of-sight path between radio link terminals, transmitting and receiving antennas and is used for prediction of the received signal strength when transmitter and receiver have obvious, unobstructed LOS path between them [5] . The received signal strength in function of the distance between those terminals and other parameters is given by the following equation:
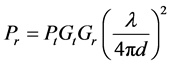 (1)
(1)
where Pt is the transmitted signal power, Pr is the received signal power,  and
and  are the transmitter and receiver antenna gains respectively and λ is the wavelength.
are the transmitter and receiver antenna gains respectively and λ is the wavelength.
The path loss can be calculated by:
 (2)
(2)
2) Log-distance path loss model
This model helps to forecast the path loss of a signal in a given environment. The general form of the path loss model is made by changing the free-space path loss with the path loss exponent n that varies with the environment.
The path loss exponent n is used to express as function of distance the average large-scale path loss for any transmitter-receiver separation. The path loss exponent n takes 2 as value for free space path loss model and it has a larger value in the presence of obstructions. This model is written as:
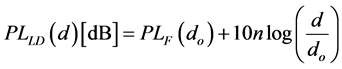 (3)
(3)
where do is a reference distance at which the path loss presents the characteristics of free space loss and d is the given path distance. The distance do = 1 km for a cellular system with a cell radius greater than 10 km and also do = 100 m or 1m for a macro cellular system with a cell radius of 1km or a microcellular with a very small radius [5] .
Table 1 shows Path loss exponent values for different environments.
3) Log-normal shadowing model
This model lets the receiver at the same distance d to have a different path loss, which varies with the random shadowing effects Xσ.
![]()
Table 1. Path loss exponent for different environments [5] .
The following equation is useful for modeling the path loss using log-normal shadowing:
 (4)
(4)
From Equation (3), we have the extended equation of log-normal shadowing model:
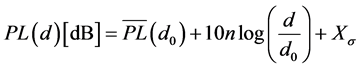 (5)
(5)
where 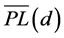 is the average large-scale path loss (in dB) at a distance d; Xσ is a zero-mean Gaussian distributed random variable (in dB) with standard deviation σ (also in dB) and
is the average large-scale path loss (in dB) at a distance d; Xσ is a zero-mean Gaussian distributed random variable (in dB) with standard deviation σ (also in dB) and 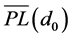 is usually calculated assuming free space propagation model between transmitter and the reference distance d0. The same value can be determined through measurements.
is usually calculated assuming free space propagation model between transmitter and the reference distance d0. The same value can be determined through measurements.
The Q-function can be used to calculate the probability that the path loss PL(d) is less a particular value [6] :
 (6)
(6)
where the path loss, PL, can take l as its local value. The Q-function has the property which is written as:
 (7)
(7)
The path loss is a random variable with a normal distribution in dB about the mean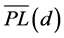 . As a result, the path loss takes the following characteristic [7] :
. As a result, the path loss takes the following characteristic [7] :
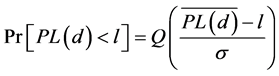 (8)
(8)
This means that the probability that the path loss 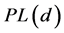 is less than a certain value l is given by the Q- function.
is less than a certain value l is given by the Q- function.
As an example, from our data, let us see how to determine the path loss related to zero-mean normally distributed random variable ![]() if we desire 95% coverage, as stated in (9). The path length for Gahengeri-Jali link is 34.54 km, but for Gahengeri-Kibungo link, it 33.41 km.
if we desire 95% coverage, as stated in (9). The path length for Gahengeri-Jali link is 34.54 km, but for Gahengeri-Kibungo link, it 33.41 km.
Using Q-function formula in (6), the probability P = 0.05 occurs for l = 1.645. The value l is given by:
![]() (9)
(9)
In this equation, we use the approximate value of standard deviation, ![]() , from measurements of path loss. For Gahengeri-Jali link, the value of
, from measurements of path loss. For Gahengeri-Jali link, the value of ![]() is 76.90 dB where for Gahengeri-Kibungo link,
is 76.90 dB where for Gahengeri-Kibungo link, ![]() is equal to 68.47 dB.
is equal to 68.47 dB.
Therefore, from Equation (9), the fade depths ![]() for the above links are 126.5 dB and 112.6 dB.
for the above links are 126.5 dB and 112.6 dB.
3. Probability Distributions for Large-Scale Fading
1) Normal distribution
This distribution is applied to all real-valued continuous random variables. It is used as an approximation function to describe fluctuation of those variables around their single mean value. As the path loss is a random variable L, its probability density function is given by [4]
![]() (10)
(10)
where ![]() is the mean and
is the mean and ![]() for the standard deviation the path loss which is normally distributed. In propagation, most of the variables are positive and it is preferable to represent their logarithm instead of their direct value [8] .
for the standard deviation the path loss which is normally distributed. In propagation, most of the variables are positive and it is preferable to represent their logarithm instead of their direct value [8] .
2) Lognormal distribution
This model describes statistically shadowing that can affects Line-of-sight (LOS). In this case, logarithmic decrease of received signal strength with respect to distance is estimated. The distribution of received signal strength is described by a normal distribution and is expressed as [3] [5] :
![]() (11)
(11)
where ![]() is defined as a deterministic model at reference distance
is defined as a deterministic model at reference distance ![]() and
and ![]() is the path loss factor (dB) written as:
is the path loss factor (dB) written as:
![]() (12)
(12)
where ![]() is the path loss exponent which depends on the environment under consideration and
is the path loss exponent which depends on the environment under consideration and ![]() represents the shadowing variance of this distribution.
represents the shadowing variance of this distribution.
However, the log-normal distribution is the distribution of a positive variable whose logarithm has a normal distribution. It is possible therefore to represent directly the probability density function:
![]() (13)
(13)
where ![]() and
and ![]() are the mean and the standard deviation not of the variable x but of the logarithm of this variable [8] .
are the mean and the standard deviation not of the variable x but of the logarithm of this variable [8] .
4. Case Study
We conducted a survey of the proposed measured radio links from the network of MTN Rwanda in Eastern province of Rwanda. The collected data are for a period of six months for two existing radio links, Gahengeri-Kibungo and Gahengeri-Jali. For each radio link, the received power values were measured using Aviat Networks Portal. We collected the transmitted power values, the radio path lengths, the transmission frequencies, the antenna heights and the antenna gains. We consider the data for a period of six months, from January to June 2014.
The calculation of the difference between the transmitted power and the values of received powers will help to obtain the total path loss for each link.
Table 2 shows the monthly average received power measured in milliwatts for the two radio links, Gahengeri-Kibungo and Gahengeri-Jali for a period of six months, from January to June 2014.
1) Monthly average received power for each link
The received power is expressed in milliwatts. According to Figure 1, the highest average received power is observed in May. This highest value of received power corresponds to the lowest loss for the link Gahengeri-Jali.
From Figure 2, the highest average received power is observed in March, which also corresponds to the lowest loss for the link Gahengeri-Kibungo. The large fluctuation is observed during April and the reason may be to that this is the period of rain in Rwanda and the rain may cause the attenuation of the signal.
For the link Gahengeli-Jali, the loss is very large in January.
![]()
Table 2. Monthly average received power.
![]()
Figure 1. Variation of monthly average received power, Gahengeri-Jali link.
![]()
Figure 2. Variation of monthly average received power, Gahengeri-Ki- bungo link.
2) Total path loss observed during 6 months for each link
Figure 3 and Figure 4 present the total Path Loss observed during six months for each link. It is clear that the path loss for Gahengeri-Jali link is higher than the path loss of Gahengeri-Kibungo link.
![]()
Figure 3. Total path loss during 6 months, Gahengeri-Jali link.
![]()
Figure 4. Total path loss during 6 months, Gahengeri-Kibungo link.
3) Comparison of normal and log-normal distributions for path loss
Calculating the difference in decibels (dB) for each measured received power, we obtain the total path loss for each radio link. We then determine the empirical pdf (measured pdf) of the path loss variation using numerical methods. To select the best model, we have to use the integral of square error (ISE) which is the sum of differences squared between measured pdf values and estimated pdf values.
The analysis of data was done by using MATLAB and the QI Macros 2014 in Excel software. This analysis will help to know the best path loss model.
5. Results
1) Comparison of path loss models as function of path length, d.
2) Comparison of normal and log-normal distributions for path loss.
Table 3 shows calculated ISE values for normal distribution and lognormal distribution models for the two links Gahengeri-Jali link and Gahengeri-Kibungo.
6. Discussions
According to Figure 5, it is observed that the path loss increases, as expected, with increasing radio path length. This signal attenuation shows that the total path loss includes the effects of distance from transmitter to receiver. The free-space path loss (in red) and log-distance path loss were plotted in MATLAB using Equations (2) and (3), respectively. They are path losses for two radio links because the links have the same frequency. The difference is the path length. The loss is lower for log-distance path loss model. If the shadowing is included in the total path loss, as it is modeled by the log-normal path loss model, the zero-mean Gaussian random variable Xσ (in dB) with standard deviation σ has to contributed to the path loss value. We have two graphs for two radio links because the standard deviation of this random variable depends on the distribution of the path loss for each link. The link that presents the higher log-normally distributed path loss value is Gahengeri-Jali (GJ) with long path length, as it is shown on Figure 5.
We observed that signal quality on radio links in Rwanda is mainly affected the attenuation of received signals due diffraction (because of highest points in Rwanda), reflection (because many mountains). High frequencies can sometimes contribute to this signal attenuation.
We presented models for determining the probability density function (pdf) of the path loss for the studied radio links as means of predicting the path loss variation. The models are based on the variation of the signal strength obtained from the difference between the transmitted power and the variation of the received power values during six months.
Combining the results of ISE and Figure 6 and Figure 7, we conclude that the best fitting model is normal distribution.
This means that the large scale fading for radio propagation in Rwanda follow the normal distribution model. In fact, for two different links, one in the Eastern province of Rwanda (Gahengeri-Kibungo) and another in Central of Rwanda (Gahengeri-Jali), their best fitting model is the same (the normal distribution).
![]()
Figure 5. Comparison of path losses from semi-empirical relations (2), (3) and (4).
![]()
Figure 6. Comparison of path loss models, Gahengeri-Jali link.
![]()
Figure 7. Comparison of path loss models, Gahengeri-Kibungo link.
![]()
Table 3. ISE values for studied models.
About the validity of findings, the results obtained are reliable since the used data were collected from industry. These results may be applied in any field.
7. Conclusions
The radio propagation in Rwanda especially for large scale is characterized by path loss that may be due to reflection, diffraction, scattering and atmospheric conditions that cause the absorption of the signal and climatological conditions like rain that causes significant fluctuations of the signal and then leads to a low received power.
However, during the design of radio links in Rwanda, one should consider the path loss and the model by using the normal distribution to get a reliable radio link. In fact, the normal distribution was found to be the best fitting model to the measured probability density function.