Load Static Models for Conservation Voltage Reduction in the Presence of Harmonics ()
Received 1 December 2015; accepted 13 February 2016; published 16 February 2016

1. Introduction
Conservation Voltage Reduction (CVR) is a method of energy reduction consumption resulting from a reduction of feeder voltage [1] . According to Schneider [1] while in North America there are numerous CVR systems deployed in distribution feeders, the majority of the results published are based on empirical field measurements. Consequently, it is not possible to extrapolate the results of this technology on other distribution feeders. To obtain a better evaluation, it is necessary to use load models and analyse the combination of these models in simulation processes.
The load model for CVR analysis is a mathematical representation of the relationship between the active and reactive power consumed and load feed voltage; in other words, it describes the load behavior when it is connected on power grid considering the voltage variation. Such models can be done without thermal cycles or static [1] [2] where the power at each instant, t, is expressed as function of voltage and frequency at the same instant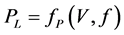 ,
, ; or dynamic, where the power is expressed as function of voltage and frequency both at past and present time [2] .
; or dynamic, where the power is expressed as function of voltage and frequency both at past and present time [2] .
Loads without thermal cycles consume energy in a time-invariant manner, with the exception of voltage variations. Specifically, there is no control feedback loop. As an example, a light bulb will consume energy when turned on, as a function of voltage in a fixed manner. In contrast, a load with a thermal cycle, such as a water heater, will have a varying duty cycle dependent on the supply voltage, Schneider [1] .
The load model, according to Price et al. [2] , may bring benefits in planning studies, in electrical power systems operation, resulting in, for example, reduction of system modifications and equipment investments, and system preventing emergencies due to better operating limits.
Some researchers found in literature demonstrate the importance of load model application on Conservation Voltage Reduction (CVR) [1] -[11] . In 1992, a research developed by Electric Power Research Institute (EPRI) [3] presented tests in order to verify the reduction voltage effects in the efficiency of loads existing in residential, commercial and industrial sectors. Such tests were divided in two parts. In the first part, data were collected to model energy consumption as a function of supply voltage. In the second part, the collected data were used to model the loads. In 1989, a field test was performed in Snohomish [4] in four circuits connected to three substations whose loads were predominantly residential and commercial, where there were alternating cycles with nominal voltage and low voltage every 24 hours. In each substation, power meters were installed to collect active power, reactive power and voltage in each phase of the test circuit, where the data were collected every 15 minutes. The test resulted in a reduction of energy consumption. However the result was not considered optimal because each substation at each instant of time had different loads connected. It is evident that the load model is needed for predicting energy saved as a result of applying the CVR method. In 2010, the study described in Schneider [1] presented the CVR application in some feeders, where the static loads were modeled by a polynomial model (ZIP), and the dynamic loads were modeled by an equivalent thermal parameter (ETP) model. The dynamic loads used a more complex model due to the control system in each load that determines the moment when it is energized and for how long.
None of those publications consider the nonlinear characteristics of the load. The contribution of the harmonics in the load behavior has to be considered in the analysis. This paper evaluates three model static load techniques as used in literature, without any consideration of nonlinearities and including their analyses. This paper is divided as following: Firstly three CVR model techniques were presented. These techniques can be applied considering or not the harmonics components presence. Then, in the second part the approach differences were shown. To obtain the model using the measured data, it was presented the parameter estimation technique. It is desired to maintain the physics aspects of the model; then the ellipsoid algorithm (using restrictions) and its application were presented. Finally the used methodology was shown as well as the results. The comparison has been done and the conclusions were shown.
2. End-User Load Modeling―Static Loads
End-user load models are mathematical functions used to describe the behavior of commercial or residential loads considering the active and reactive power as function of both variables: voltage and sometimes frequency. The static models used to represent the load are performed in two main types: by an exponential model and by polynomial models, also known as ZIP models [1] [2] [5] [7] .
2.1. Exponential Model―EXP
In exponential models the relationship between the consumed power and the feed voltage is given by an exponential function, as in Equation (1) for the active power and in Equation (2) for the reactive power [2] [5] [10] - [12] :
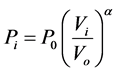 (1)
(1)
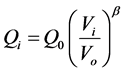 (2)
(2)
where 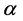 and
and  parameters describe the load behavior.
parameters describe the load behavior.
When both coefficients 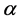 and
and 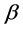 are equal to zero, it means that the load behaves as Constant Power. In case of both
are equal to zero, it means that the load behaves as Constant Power. In case of both  and
and 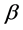 are equal to one, the load behaves as Constant Current; and finally if both coefficients are equal to two, the load behaves as Constant Impedance.
are equal to one, the load behaves as Constant Current; and finally if both coefficients are equal to two, the load behaves as Constant Impedance.
2.2. ZIP Model (ZIP)
In polynomial models, ZIP model, the load is represented by following some physical characteristics. Some equipment, such as electronic ballasts, have constant power consumption under voltage variation. On the other hand, others behave as a combination of two or three of the following characteristics: Constant Impedance (Z), Constant Current (I) and Constant Power (P).
The expressions for active and reactive power (Pi, Qi) of the ZIP model are presented by Equations (3) and (4) respectively. For both Equations, the coefficients have to obey the constraints presented in Equation (5). The relationship between power consumption and voltage magnitude is given by a polynomial Equation [2] [5] [7] [10] [11] :
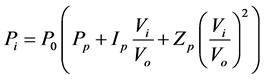 (3)
(3)
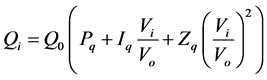 (4)
(4)
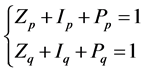 (5)
(5)
where:
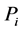 : Active power consumption of the ith load.
: Active power consumption of the ith load.
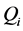 : Reactive power consumption of the ith load.
: Reactive power consumption of the ith load.
![]() : Active power consumption at nominal voltage.
: Active power consumption at nominal voltage.
![]() : Reactive power consumption at nominal voltage.
: Reactive power consumption at nominal voltage.
![]() : Actual terminal voltage.
: Actual terminal voltage.
![]() : Nominal terminal voltage.
: Nominal terminal voltage.
![]() : Fraction of load that is Constant Impedance.
: Fraction of load that is Constant Impedance.
![]() : Fraction of load that is Constant Current.
: Fraction of load that is Constant Current.
![]() : Fraction of load that is Constant Power.
: Fraction of load that is Constant Power.
2.3. Modified ZIP Model―(ZIP_mod)
Schneider et al. [1] proposed a new ZIP model where, besides the information about the Constant Impedance, Constant Current and Constant Power, there is also information about the phase angle of each one of these components. In this case, both active and reactive Equations are coupled. The active and reactive power calculus is given in Equations (6) and (7) respectively, obeying the constraint in Equation (8):
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
where:
![]() : Real power consumption of the ith load.
: Real power consumption of the ith load.
![]() : Reactive power consumption of the ith load.
: Reactive power consumption of the ith load.
![]() : Actual terminal voltage.
: Actual terminal voltage.
![]() : Nominal terminal voltage.
: Nominal terminal voltage.
![]() : Apparent power consumption at nominal voltage.
: Apparent power consumption at nominal voltage.
![]() : Fraction of load that is Constant Impedance.
: Fraction of load that is Constant Impedance.
![]() : Fraction of load that is Constant Current.
: Fraction of load that is Constant Current.
![]() : Fraction of load that is Constant Power.
: Fraction of load that is Constant Power.
![]() : Phase angle of the Constant Impedance component.
: Phase angle of the Constant Impedance component.
![]() : Phase angle of the Constant Current component.
: Phase angle of the Constant Current component.
![]() : Phase angle of the Constant Power component.
: Phase angle of the Constant Power component.
In any ZIP model, when the load is represented as Constant Impedance, it means that the power varies directly with the square of the voltage; in the case of the Constant Current, the power varies directly with the voltage; and, lastly, if the load is modeled as Constant Power, the power does not vary when the voltage varies [2] .
3. Analysing the Harmonics Presence and Its Effect in the Model
None in all presented models is mentioned about harmonic components in any reference although its presence affects the data. Once measurements are used to obtain the parameters for each model, and as the components suffer influences from harmonics, it is necessary to discuss how to consider its influence before start using the data.
3.1. For Sinusoidal Voltage and Current
The apparent power measured by the equipment gives us two parcels called P and Q. For sinusoidal source supplying a linear load, these parcels are [13] :
![]() (9)
(9)
where:
V: RMS voltage.
V1: Fundamental voltage.
V1: Fundamental current.
S: Apparent power.
P1: Fundamental active power.
Q1: Fundamental reactive power.
PM: Measured active power.
QM: Measured reactive power.
3.2. For Nonsinusoidal Voltage and Current
Considering nonsinusoidal source supplying a nonlinear load, however, the apparent power assumes a different value including the harmonics effect. The measured active power PM now has also the contribution of the harmonic active power PH. Similarly the measured reactive power QM is not only composed by Q1 but also by a sum of other parcels, namely DV, DI and DH. This measured power should no longer be called reactive power, but nonactive power, [13] . The demonstration is presented below:
![]() (10)
(10)
consequently,
![]() (11)
(11)
![]() (12)
(12)
where:
V1: Fundamental voltage.
VH: Harmonic voltage.
I1: Fundamental current.
IH: Harmonic current.
S: Apparent power.
P1: Fundamental active power.
Q1: Fundamental reactive power.
PM: Measured active power.
QM: Measured reactive power.
DV: Voltage distortion power.
DI: Current distortion power.
PH: Harmonic active power.
DH: Harmonic distortion power.
N: Nonactive power.
4. Parameter Estimation
The parameter estimation is a procedure which uses some samples from measurements to calculate one or more unknown parameters. The used measurements (samples) in the estimation process are subject to errors, so that the estimated parameters also have associated errors [14] . Equation (13) shows the value of the samples obtained by a measurement device. The measured value is close to the true value, but with the difference of an error.
![]() (13)
(13)
where ![]() is the value obtained by measurement equipment;
is the value obtained by measurement equipment; ![]() is the true value of the measurement; and
is the true value of the measurement; and ![]() is the random measurement error that serves to model the uncertainty in the measurements.
is the random measurement error that serves to model the uncertainty in the measurements.
The statistical criteria used in the parameter estimation may be quoted the maximum likelihood, where the goal is to maximize the probability that the estimated state variable is the actual value of the state variable vector [14] . Such estimator assumes that the probability density function (PDF) is known. Other criteria may also be used, for example, the weighted least-squares criterion that aims to minimize the sum of the weighted squares of the estimated measure deviations. In this case, it is not required that the PDF of samples or measurement errors be known, but it is assumed to have Gaussian normal distribution [14] .
In the maximum likelihood criterion, it is necessary to estimate the variable x that maximizes the likelihood of measuring ![]() [14] . According to the author, the maximum likelihood estimate of the unknown parameter is thus expressed as the parameter value that minimizes the sum of squares of the difference between each measured value and the actual measured value, with each squared difference weighted by the variance of the meter error, as in (14):
[14] . According to the author, the maximum likelihood estimate of the unknown parameter is thus expressed as the parameter value that minimizes the sum of squares of the difference between each measured value and the actual measured value, with each squared difference weighted by the variance of the meter error, as in (14):
![]() (14)
(14)
where:
![]() : function used to calculate the value being measured by the ith measurement.
: function used to calculate the value being measured by the ith measurement.
![]() : measurement residual.
: measurement residual.
![]() : number of independent measurements.
: number of independent measurements.
![]() : variance of the ith measurement.
: variance of the ith measurement.
![]() : ith measurement.
: ith measurement.
In one matrix approach, this Equation can be written as in (15):
![]() (15)
(15)
where: R: covariance matrix of the measurements, as can be seen in (16).
![]() (16)
(16)
5. Ellipsoid Algorithm
This algorithm consists in finding a solution to the optimization problem through a succession of increasingly smaller ellipsoids, starting from the initial ellipsoid containing the optimal point [15] .
Given the constrained optimization problem described in (17) [12] , the convergence is achieved if the objective function and the constraints are convex and if ![]() [16] . The algorithm starts with an ellipsoid
[16] . The algorithm starts with an ellipsoid ![]() centered at the
centered at the ![]() point as in (18):
point as in (18):
![]() (17)
(17)
![]() (18)
(18)
where:
![]() : depicts the constraints of inequality,
: depicts the constraints of inequality,
![]() : represents equality constraints described as two inequality constraints, and
: represents equality constraints described as two inequality constraints, and
![]() : objective function.
: objective function.
The ellipsoid algorithm can be described by recursive Equations (19), (20) and (21), which generate a sequence of ![]() points [12] .
points [12] .
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
where m is the gradient or sub-gradient of the function or of the most violated constraint, according to the rule described in (22) and (23) [12] .
![]() (22)
(22)
![]() (23)
(23)
Figure 1 illustrates the flowchart of the ellipsoid algorithm. Firstly, the variables that define i. the region which is contained in the solution (Q) (initial ellipsoid), ii. initial optimal solution (xopt) and its objective function value (fopt), and iii. the algorithm parameters (for example the tolerance for calculate the gradient numerically (tol)) are initialized. After that, the variable receives the value of the largest constraint function at x. Then the objective function value at the point x is calculated. If r is negative, the algorithm calculates the objective function gradient at point x (fx) and checks whether the value of fk is smaller than the optimal value achieved so far. If fk is smaller than fopt (optimal function value), xopt and fopt receive the value of xk and fk, respectively, otherwise the algorithm goes to the next step. If r is bigger than or equal to zero, the algorithm calculates the gradient of the most violated constraint. In the next step, the algorithm computes the variables to generate the next ellipsoid based on the computed gradient vector. This process is repeated until the convergence is achieved.
6. Method to Obtain the Model
The data measurements were performed three times for each load and at different times. During the experiments, the voltage has been changed in steps. An energy analyzer was used to collect data. Every 5 minutes the input voltage was increased by five volts starting the measurement at 110 V and ending at 130 V. The nominal voltage is 127 V. Samples were collected every second. For each load, it was used at least 4500 measurements. These data were used in the following models.
For the exponential model, the optimization problem is given as in Equation (24) [6] :
![]() (24)
(24)
where: ![]() and
and ![]() is the function described in (1). The same formulation is presented for the exponential reactive power model.
is the function described in (1). The same formulation is presented for the exponential reactive power model.
For ZIP model [2] the parameters are estimated according to the optimization problem presented in Equation (25) [6] :
![]()
Figure 1. Flowchart of the ellipsoid algorithm.
![]() (25)
(25)
where:
![]() ;
;
![]() is the active power at nominal voltage and
is the active power at nominal voltage and ![]() is the function described in (3).
is the function described in (3).
The same formulation is presented for the ZIP reactive power model [2] .
For the ZIP_mod model [1] , the estimated parameters must satisfy simultaneously the Equations of active and reactive power, so that the optimization problem is defined as in Equation (26):
![]() (26)
(26)
where: ![]() in order to minimize both active and reactive power functions at the same intensity;
in order to minimize both active and reactive power functions at the same intensity; ![]() is the Equation concerning the active power with
is the Equation concerning the active power with ![]() given according to Equation (6);
given according to Equation (6); ![]() is the Equation related to reactive power with
is the Equation related to reactive power with ![]() as in Equation (7); and
as in Equation (7); and ![]() is the apparent power consumption at nominal voltage.
is the apparent power consumption at nominal voltage.
The model proposes to minimize the active and reactive power functions simultaneously through a weighted sum, that is, both power functions are minimized with the same weight. Often the objective functions (active and reactive power) have different magnitude order. Therefore, one function can be minimized faster than the other. To solve this problem, the optimal objective function was calculated for the active power (![]() ) and reactive (
) and reactive (![]() ) separately using the constraints of Equation (26), and then, the optimal values obtained were used to calculate the objective function of the problem in Equation (27):
) separately using the constraints of Equation (26), and then, the optimal values obtained were used to calculate the objective function of the problem in Equation (27):
![]() (27)
(27)
This paper uses the Ellipsoid optimization technique for parameter estimation obeying the model constraints described on Equations (24), (25) and (26).
7. Methodology
Knowing load mathematical models, it is possible to obtain a model of a group of loads by simply adding the single models, that is, the procedure used for linear loads (superposition theorem). In order to analyse the effect of the harmonics in the load models and in their aggregation, an experiment is carried out with six different loads, and the analysis is divided in two phases.
1) During the first phase, each equipment has been tested for different voltage values in the range of 0.9 and 1.05 pu. The measurements have been made repeatedly and the variables S, S1, P, P1, N, Q1 have been registered. Using the two groups of variables (S1, P1, Q1 and S, P, N) the mathematical models have been obtained by following the procedure previously mentioned. Consequently, two representations (i. only the fundamental frequency components (S1, P1, Q1) and ii. harmonics contributions (S, P, N)) have been calculated for each of the three models (Exponential, ZIP and ZIP_mod) and for each equipment.
2) In the second phase, six pieces of equipment were connected simultaneously and the measurements for the same variables shown in phase 1 have been collected. Six models have been adjusted, two representations for the two groups of variables (i. only the fundamental frequency components (S1, P1, Q1) and ii. harmonics contributions (S, P, N)) for each method (Exponential, ZIP and ZIP_mod).
8. Results
Following the methodology, the experiments have been done and the results are presented in this section. Table 1 contains the modeled loads and their rated power. Among the modeled loads, there are resistive loads, electronics and motors.
8.1. Phase 1―Models Obtained for Each Load
Figure 2(a) is presented to illustrate how the active powers P and P1 varies when the voltage changes in steps. They are almost the same, as the active harmonic power PH is very low. Otherwise Figure 2(b) shows a big difference between QM (that in fact is N) and Q1. Figure 3 presents similar results for Liquid Crystal Display measurements. In this case the difference between active powers P and P1 is more evident. Using these data, the models, as a function of voltage, Exp, ZIP and ZIP_mod, are obtained.
Table 2 presents the parameters ![]() and
and ![]() for the exponential model expressed by Equation (7) and (8) for all modeled loads, considering the measured data (P, N) and the filtered data (P1, Q1). As the active power suffers little influence of harmonics, the calculated parameters (
for the exponential model expressed by Equation (7) and (8) for all modeled loads, considering the measured data (P, N) and the filtered data (P1, Q1). As the active power suffers little influence of harmonics, the calculated parameters (![]() , Po) are almost equal, even for models considering or not harmonics contribution. Otherwise, the nonactive power is strongly influenced by the presence of harmonics.
, Po) are almost equal, even for models considering or not harmonics contribution. Otherwise, the nonactive power is strongly influenced by the presence of harmonics.
![]() (a) (b)
(a) (b)
Figure 2. Compact fluorescent measurements. (a) Active power (P1, Pm) and voltage variation; (b) Nonactive power (Q1, N) and voltage variation.
![]() (a) (b)
(a) (b)
Figure 3. Liquid crystal display measurements. (a) Active power (P1, P) and voltage variation; (b) Nonactive power (Q1, N) and voltage variation.
![]()
Table 2. Exponential model parameters for active and nonactive power.
Table 3 presents the parameters for active and nonactive power Equation considering the ZIP model. It can be seen that there are some subtle differences in active Equation parameters, mainly for the nonlinear loads like CFL, LCD and TV. On the other hand, significant differences are observed for nonactive power parameters. In fact the model parameters for nonactive power are completely different.
For Modified ZIP model, the results are presented in a different way. As the Equations of active and reactive power are coupled, the results are presented in Table 4, each one for different reference data S1, P1, Q1 and S, P, N respectively. It can be seen that the results are strongly affected by the presence of harmonics.
8.2. Phase 2―Load Aggregation
In the second phase the modeled loads, used in phase I, are turned on in the same time, and measurements of total active and nonactive power are done. Using these data, the models for the group of equipments data are obtained (Collective Model). Table 5, Table 6 and Table 7 present the obtained models.
Finally, the model obtained by summing up the individual models is calculated (Sum of Models) by applying superposition theorem used in Equation (28).
![]() ,
,![]() (28)
(28)
Table 8 presents a comparison among the obtained models outputs (Collective Model and Sum of Models), considering or not harmonics components (i. only the fundamental frequency components (S1, P1, Q1) and ii. harmonics contributions (S, P, N)), for two different voltage levels (110 and 130V). The line of the measured
![]()
Table 3. ZIP model parameters for active and nonactive power.
![]()
Table 4. Modified ZIP model parameters for active and nonactive power.
![]()
Table 5. Exponential model parameters for active and nonactive power.
![]()
Table 6. ZIP model parameters for active and nonactive power.
![]()
Table 7. Modified ZIP model parameters for active and nonactive power.
aThese values were obtained using the model built using data for all equipment turned on simultaneously; bThese values were obtained using the model built using the sum of individual models.
*Corresponding author.
9. Conclusion
This paper demonstrated the application of optimization technique for the treatment of ellipsoid constraints of three static load models widely used in the literature. This technique was used in order to obtain real models for the loads, so that the result achieved can produce physical meaning. All the mathematical formulations, as well as the methodology used to achieve the results are available in the initial sections.
For most of the loads, the three models showed similar results, except for electronic loads such as compact fluorescent lamp, monitor, computer and television. Such loads showed a reduction in power consumption with the increase in voltage level. Thus, it was evident that among the three physical models presented, only the ZIP_mod can faithfully represent the load, once the other models do not show curves with negative slope.
The literature presents these models and suggests using the superposition theorem to obtain the model which represents a group of loads by simple summing up the individual models. This paper shows that the results of the obtained models, which do not filter the data (use only the fundamental frequency), cannot be used for load aggregation. In other words, to apply this kind of load model it is necessary to work with only the filtered data of the load, otherwise the final model will present very significant errors.
Acknowledgements
W.D. Caetano thanks CAPES (Coordination of improvement of Higher Education Personnel) for financial support.
NOTES
![]()
*Corresponding author.