The Schultz Index and Schultz Polynomial of the Jahangir Graphs J 5, m ()
Received 13 November 2015; accepted 28 December 2015; published 31 December 2015
1. Introduction
Let G be simple connected graph with the vertex set V(G) and the edge set E(G). For vertices u and v in V(G), we denote by d(u, v) the topological distance i.e., the number of edges on the shortest path, joining the two vertices of G.
A topological index is a numerical quantity derived in an unambiguous manner from the structure graph of a molecule. As a graph structural invariant, i.e. it does not depend on the labelling or the pictorial representation of a graph. Various topological indices usually reflect molecular size and shape.
As an oldest topological index in chemistry, the Wiener index was first introduced by Harold Wiener [1] in 1947 to study the boiling points of paraffin. It plays an important role in the so-called inverse structure-property relationship problems. The Wiener index of G is defined as [1] -[7] :
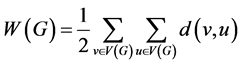
The Hosoya polynomial was introduced by Haruo Hosoya, in 1988 [8] and defined as follows:
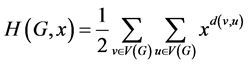
The number of incident edges at vertex v is called degree of v and denoted by dv.
The Schultz index of a molecular graph G was introduced by Schultz [9] in 1989 for characterizing alkanes by an integer as follow:
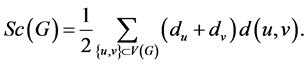
The Modified Schultz index of a graph G was introduced by S. Klavžar and I. Gutman in 1996 as follow [10] :
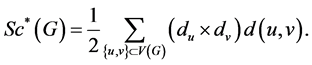
Also the Schultz and Modified Schultz polynomials of G are defined as:
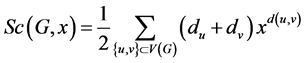
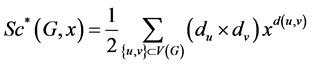
where du and dv are degrees of vertices u and v.
The Schultz indices have been shown to be a useful molecular descriptors in the design of molecules with desired properties, reader can see the paper series [11] - [29] .
In this paper computation of the Schultz and Modified Schultz indices of the Jahangir graphs J5,m are proposed. The Jahangir graphs J5,m 
is defined as a graph on 5m + 1 vertices and 6 m edges i.e., a graph consisting of a cycle C5m with one additional vertex (Center vertex c) which is adjacent to m vertices of C5m at distance 5 to each other on C5m. Some example of the Jahangir graphs and the general form of this graph are shown in Figure 1 and Figure 2 and the paper series [30] - [35] .
![]()
Figure 1. Some examples of the Jahangir graphs J5,3, J5,4, J5,5, J5,6 and J5,8.
![]()
Figure 2. A general representation of the Jahangir graphs 
n = 5,
.
2. Results and Discussion
In this present section, we compute the Schultz and Modified Schultz indices and the Schultz and Modified Schultz polynomials of the Jahangir graphs 
n = 5, 
as.
Theorem 1. Let J5,m be the Jahangir graphs for all integer numbers![]()
. Then, the Schultz, Modified Schultz polynomials and indices are as:
The Schultz index and polynomial are equal to
・ ![]()
・ ![]()
.
The Modified Schultz index and polynomial are equal to:
・ ![]()
・ ![]()
Proof. Let J5,m be Jahangir graphs ![]()
with 5m + 1 vertices and 6 m edges. From Figure 1 and Figure 2, we see that 4 m vertices of J5,m have degree two and m vertices of J5,m have degree three and one additional vertex (Center vertex) of J5,m has degree m. Thus we have three partitions of the vertex set ![]()
as follow
![]()
![]()
![]()
Obviously, ![]()
and ![]()
thus
![]()
Now, for compute the Schultz and Modified Schultz indices and the Schultz and Modified Schultz polynomials of the Jahangir graphs![]()
, we see that for all vertices u, v in ![]()
and the diameter of the Jahangir graph J5,m is equal to![]()
.
Now, we compute all cases of d(u,v)-edge-paths ![]()
of J5,m in Table 1.
![]()
Table 1. All cases of ![]()
-edge-paths ![]()
of the Jahangir graph J5,m.
For example, in case![]()
; one can see that there are ![]()
1-edges paths between the vertex c and vertices from V3 (where![]()
). There exist two 1-edges paths starts every vertex ![]()
until ![]()
(where![]()
). There are 3 m 1-edges paths between two vertices ![]()
(two adjacent vertices or edges), such that![]()
. Thus, the first terms of the Schultz and Modified Schultz polynomials of J5,m are equal to ![]()
and ![]()
respectively.
Also, in case![]()
; there are two 2-edges paths between Center vertex ![]()
and other vertices of vertex set![]()
. ![]()
2-edges paths between all vertices of
![]()
and ![]()
2-edges paths start from vertices of ![]()
until vertices of ![]()
and![]()
. Thus, the second terms of the Schultz and Modified Schultz polynomials of ![]()
are equal to ![]()
and![]()
, respectively.
By using the definition of the Jahangir graphs and Figure 1 and Figure 2, we can compute other terms of the Schultz and Modified Schultz polynomials of J5,m. We compute and present all necessary results on based the degrees of du & dv for all cases of ![]()
-edge-paths ![]()
in following table.
Now, we can compute all coefficients of the Schultz ![]()
and Modified Schultz ![]()
polynomials and indices of J5,m by using all cases of the ![]()
-edge-paths ![]()
of the Jahangir graph J5,m in Table 1 and alternatively
![]()
From the definition of Schultz index and the Schultz Polynomial of G, we can compute the Schultz index of the Jahangir graph J5,m by the first derivative of Schultz polynomial of J5,m (evaluated at x = 1) as follow:
![]()
And also Modified Schultz polynomial of J5,m is equal to
![]()
And from the first derivative of Schultz Modified polynomial of the Jahangir graph J5,m (evaluated at x = 1), the Modified Schultz index of J5,m is equal to:
![]()
Here these completed the proof of Theorem 1. ■
Acknowledgements
The authors are thankful to Professor Emeric Deutsch from Department of Mathematics of Polytechnic University (Brooklyn, NY 11201, USA) for his precious support and suggestions. The research is also partially supported by NSFC (No. 11401519).
NOTES
![]()
*Corresponding author.