Rayleigh-Benard Instability in a Horizontal Porous Layer Affected by Rotation ()
Received 13 November 2015; accepted 27 December 2015; published 30 December 2015

1. Introduction
In recent years, considerable attention has been paid to thermal instability theory in fluid. The convection in a thin horizontal layer of fluid heated from below is well suited to illustrate the many facts, mathematical and physical, of the general theory of hydrodynamic stability. The earliest experiments demonstrated the onset of thermal instability in fluids, are those of Benard [1] [2] . Rayleigh [3] provided a theoretical basis for Benard’s experimental results. The instability of a layer of fluid heated from below and subjected to Coriolis forces have been studied by Chandrasekher [4] and Chandrasekher and Elbert [5] for stationary convection and overstability respectively.
The stability of Benard problem for a fluid in a porous medium has been examined by Horton and Rogers [6] , Lapwood [7] , Wooding [8] , and Elder [9] using Darcy’s law. A modification of Darcy’s law has been suggested by Brinkman [10] [11] . There has been considerable interest in the study of different problems in the presence of porous medium by several authors [12] -[20] . An extensive review articles on convection in porous medium can be found in Nield and Bejan [21] .
Rotating Rayleigh-Benard convection has important applications in geophysical and astrophysical flows as well as industrial applications. Many flows in nature are driven by buoyant convection and subsequently modulated by rotation. Such systems are relevant to numerous astrophysical and geophysical phenomena, including convection in arctic ocean, in the earth’s outer core, in the interior of gaseous giant planets and the outer layer of the sun. Thus the problem is of interest in a wide range of sciences including geology, oceanography, climatology and astrophysics.
In this work Benard convection in a horizontal porous layer affected by rotation is studied for both stationary and overstability cases with different boundary conditions. Analytical and numerical solutions will be obtained. The numerical method used to solve the problem is the Chebyshev Tau method. This method is better suited to the solution of hydrodynamic stability problems than expansions in other sets of orthogonal polynomials. Several authors used this method to obtain numerical solutions of thermal stability problems [22] - [26] .
2. Problem Formulation
Consider an infinite horizontal porous layer permeated by an incompressible viscous fluid which is heated from below and confined between the planes x3 = 0, and x3 = d. The layer is subjected to a constant gravitational acceleration g in the negative x3 direction and is rotated about the x3 axis at a constant angular velocity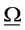 .The porous layer is controlled by the Brinkman model and the temperature T at the lower and upper boundaries are
.The porous layer is controlled by the Brinkman model and the temperature T at the lower and upper boundaries are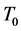 , and
, and 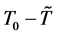 respectively. The bottom surface is assumed to be rigid and the top surface is free. A coordinate frame is selected in which the x3-axis is aligned vertically upwards.
respectively. The bottom surface is assumed to be rigid and the top surface is free. A coordinate frame is selected in which the x3-axis is aligned vertically upwards.
If the Boussinesq approximation is adopted, i.e.
 ,
,
where 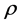 is the density of the fluid,
is the density of the fluid,  is the fluid density at temperature T0 and
is the fluid density at temperature T0 and 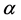 is the coefficient of volume expansion, then the governing equations of total mass, momentum and thermal energy have form
is the coefficient of volume expansion, then the governing equations of total mass, momentum and thermal energy have form
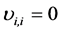 , (1)
, (1)
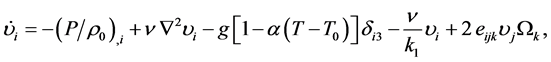 (2)
(2)
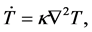 (3)
(3)
where P is the pressure, 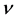 is he kinematic viscosity, k1 is the permeability of porous medium and
is he kinematic viscosity, k1 is the permeability of porous medium and 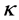 is the coefficient of thermal conductivity. We seek a time-independent basic solution of Equations (1)-(3) with temperature varying in the x3-direction, that is a solution of the form
is the coefficient of thermal conductivity. We seek a time-independent basic solution of Equations (1)-(3) with temperature varying in the x3-direction, that is a solution of the form
 (4)
(4)
Thus
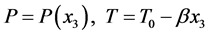 , (5)
, (5)
where 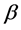 is the adverse temperature gradient.
is the adverse temperature gradient.
3. Perturbation Equations
Now let the basic solution be slightly perturbed such that
![]() .
.
Substitute in Equations (1)-(3) and linearize these equations to obtain
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
We now introduce the dimensionless variables as follows
![]() . (9)
. (9)
Then Equations (6)-(9) take the form
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
where the hat superscript has been dropped but all the variables are non-dimensional and where
![]() ,
,
![]()
The non-dimensional numbers R, N, Pr and Ta are the Rayleigh number, the permeability of porous medium, the Prandtl number and the Taylor number respectively. Apply the curl operator to Equation (11) we obtain
![]() (13)
(13)
where ![]() is the vorticity. Apply the curl operator once again to Equation (13) to obtain
is the vorticity. Apply the curl operator once again to Equation (13) to obtain
![]() (14)
(14)
The related boundary conditions are
![]() (15)
(15)
![]() (16)
(16)
4. Normal Mode Analysis
The differential Equations (12)-(14) and the boundary conditions (15) and (16) constitute a linear boundary value problem that can be solved using the method of normal modes. We write
![]() (17)
(17)
where![]() ,
, ![]() are the third components of the velocity and vorticity respectively, n, m are the wave numbers of the harmonic disturbance and
are the third components of the velocity and vorticity respectively, n, m are the wave numbers of the harmonic disturbance and ![]() is the growth rate. Substitute into the differential equations (12)-(14) to obtain
is the growth rate. Substitute into the differential equations (12)-(14) to obtain
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
where![]() ,
, ![]() and
and ![]() is the wave number. We may eliminate ξ and θ from Equations (18)-(20) to obtain
is the wave number. We may eliminate ξ and θ from Equations (18)-(20) to obtain
![]() (21)
(21)
which is an eighth order ordinary differential equation to be satisfied by w.
5. The Free Boundary Problem
Here we shall consider both boundaries to be free but later on we shall present results for the corresponding rigid boundary value problem. For the free boundary value problem,
![]()
Thus Equation (17) has eigenfunctions ![]() where A is a constant and l is an integer, then
where A is a constant and l is an integer, then ![]() where
where ![]() and
and ![]() satisfies the cubic equation
satisfies the cubic equation
![]() (22)
(22)
The solutions of (22) are functions of ![]() and R and we have to examine how the nature of these solutions depends on these variables by considering the following cases.
and R and we have to examine how the nature of these solutions depends on these variables by considering the following cases.
5.1. Case (1): When the Fluid Is Heated from Above
Here we put H = 1 in Equation (22) and we need to discuss the roots of the polynomial equation![]() . Clearly all the coefficients of
. Clearly all the coefficients of ![]() are positive and real. Thus
are positive and real. Thus ![]() has either three negative real solutions or one negative real solution and two complex conjugate solutions. To show how that the real part of the complex conjugate solutions is negative let
has either three negative real solutions or one negative real solution and two complex conjugate solutions. To show how that the real part of the complex conjugate solutions is negative let ![]() be the sum of the roots of
be the sum of the roots of ![]() then
then
![]() and we can show after some algebra that
and we can show after some algebra that![]() . Since
. Since ![]() then
then
![]() has a negative real root,
has a negative real root, ![]() , which is greater than Σ. Let
, which is greater than Σ. Let ![]() be the two complex conjugate roots of
be the two complex conjugate roots of ![]() such that
such that![]() ,
, ![]() , then
, then ![]() but
but ![]() then
then ![]() so
so![]() .
.
Thus if ![]() has only one real root and two complex conjugate roots then the real part of these conjugate solutions is negative. Hence when this fluid is heated from above, no instabilities ensue since all the roots are either negative if they are real or have negative real part if they are complex.
has only one real root and two complex conjugate roots then the real part of these conjugate solutions is negative. Hence when this fluid is heated from above, no instabilities ensue since all the roots are either negative if they are real or have negative real part if they are complex.
5.2. Case (2): When the Fluid Is Heated from Below
Here![]() , and we shall discuss the stability of the fluid for the cases of stationary and overstability.
, and we shall discuss the stability of the fluid for the cases of stationary and overstability.
5.3. Stationary Convection Case
To determine the critical Rayleigh number for the onset of stationary convection we set ![]() in Equation (22). Thus
in Equation (22). Thus
![]() (23)
(23)
The critical Rayleigh number can be obtained by minimizing R over the wave number for several values of N and![]() . Clearly
. Clearly
![]() (24)
(24)
which means that rotation has a stabilizing effect on the system, and the permeability of porous medium has a stabilizing effect on the system provided that
![]()
5.4. The Case of Overstability
To obtain the critical Rayleigh number for the overstability case we suppose that
![]() (25)
(25)
where ![]() is complex and
is complex and![]() . Thus Equation (22) reduces to
. Thus Equation (22) reduces to
![]() (26)
(26)
Equating the real and imaginary parts of this equation we obtain the following pair of equations
![]() (27)
(27)
![]() (28)
(28)
From Equation (28) we obtain
![]() (29)
(29)
from which we conclude that in order for ![]() to be positive we must have
to be positive we must have
![]() . (30)
. (30)
So in order to have overstability the condition (30) must be satisfied. This condition can be satisfied provided
1) ![]() 2)
2) ![]()
Substitute for ![]() in Equation (27) we obtain,
in Equation (27) we obtain,
![]()
from which we conclude that
![]()
![]()
i.e. rotation has a stabilizing effect on the system but the permeability of porous medium has a destabilizing effect on the system.
6. Results and Discussion
The differential Equations (18)-(20) together with the boundary conditions (15) and (16) are to be solved numerically for the case when the fluid layer is heated from below using the method of expansion of Chebyshev polynomials. We express all the variables of the problem in terms of Chebyshev polynomials in the following way
![]() .
.
Substitute into Equations (18)-(20) and the boundary conditions to obtain an eigenvalue problem of the form ![]() which is solved using the numerical routine F02BJF of the NAG package.
which is solved using the numerical routine F02BJF of the NAG package.
The relation between the Taylor number, Ta, and the critical Rayleigh number, R, for different values of the non-dimensional permeability of porous medium, N, when both boundaries are free for the stationary convection case is displayed in Figure 1. It is clear from the figure that rotation has a stabilizing effect on the system. Moreover as N increases R decreases provided that Ta is less than a certain value and when Ta exceeds that value then R increases as N increases which indicates that rotation has a profound effect on the effect of the non- dimensional permeability of porous medium. These results coincide exactly with Equations (24) in the analytic solution. In case of no porosity the critical Rayleigh number, R, is less than that of the porous medium case provided Ta is less than a certain value and when Ta exceeds that value then the critical Rayleigh number in the absence of porous medium case is always higher.
In the overstability case, the relation between the Taylor number, Ta, and the critical Rayleigh number, R, when both boundaries are free for different values of N is displayed in Figure 2. It is clear from the figure that as Ta increases, R increases which indicates that rotation has a stabilizing effect on the system in this case also. Moreover as N decreases, R increases for all values of![]() . i.e. the system becomes more stable as the porous
. i.e. the system becomes more stable as the porous
![]()
Figure 1. The relation between Ta and critical R for the stationary convection case when both boundaries are free.
medium permeability decreases. In case of no porosity the critical Rayleigh number, R, is less than the corresponding Rayleigh number in porous medium for all values of Ta.
It is important to remark that in absence of porous medium, which is the classical Benard problem under the effect of rotation, overstability appears when the Taylor number, Ta, exceeds a certain value and the Prandtl number Pr < 1. In this work this result is proved analytically and numerically in the presence of porous medium.
A comparison between the stationary convection and overstability cases when both boundaries are free is displayed in Figure 3. It is clear from the figure that overstability is the preferred mechanism provided Pr < 1 and the Taylor number, Ta, exceeds a certain critical value. This critical value of Ta increases as N decreases. Moreover for the overstability case we notice that as Pr increases the critical Rayleigh number, R, increases which indicates that the Prandtl number has a stabilizing effect on the system.
Numerical results are also obtained when both boundaries are rigid. In this case the relation between the Taylor number, Ta, and the critical Rayleigh number, R, for different values of the non-dimensional permeability of porous medium, N, for the stationary convection case is displayed in Figure 4. It is clear from the figure that as Ta increases R increases which indicates that rotation has a stabilizing effect on the system. Moreover as N increases R decreases for all values of Ta and we notice here that this conclusion is different from that in the case when both boundaries are free. In case of no porosity the critical Rayleigh number, R, is always less than the corresponding Rayleigh number in porous medium for all values of Ta.
In case of overstability, the relation between the Taylor number, Ta, and the critical Rayleigh number, R, when both boundaries are rigid for different values of N is displayed in Figure 5. It is clear from the figure that
![]()
Figure 2. The relation between Ta and critical R for the overstability case when both boundaries are free Pr = 0.05.
![]()
Figure 3. A comparison between the stationary and overstability cases when both boundaries are free and N = 0.01.
![]()
Figure 4. The relation between Ta and critical R for the stationary stability case when both boundaries are rigid.
![]()
Figure 5. The relation between Ta and critical R for the overstability case when both boundaries are rigid Pr = 0.05.
as Ta increases, R increases which indicates that rotation has a stabilizing effect on the system in this case also. Moreover as N increases, R decreases for all values of Ta. i.e. the system becomes more stable as the porous medium permeability decreases. In case of no porosity the critical Rayleigh number, R, is always less than the corresponding Rayleigh number in porous medium for all values of Ta.
A comparison between the stationary convection and overstability cases when both boundaries are rigid is displayed in Figure 6. It is clear from the figure that overstability is the preferred mechanism provided Pr < 1 and the Taylor number Ta, exceeds a certain critical value. This critical value of Ta increases as N decreases. Moreover for the overstability case we notice that as Pr increases the critical Rayleigh number, R, increases which indicates that the Prandtl number has a stabilizing effect on the system.
A comparison between the free and rigid boundaries in the stationary convection case is shown in Figure 7. Clearly the critical Rayleigh numbers, R, for the rigid boundary case are always greater than the corresponding ones of the free boundary case. For the overstability case, a comparison between the free and rigid boundaries is displayed in Figure 8. It is clear that the critical Rayleigh numbers, R, for the rigid boundary case are always greater than the corresponding ones of the free boundary case.
7. Conclusion
The Benard convection in a horizontal porous layer is investigated when the layer is affected by rotation. Analytical and numerical solutions are obtained for the stationary convection and overstability cases. The numerical results are in agreement with the analytical solutions obtained. In the free boundary problem it appears that
![]()
Figure 6. A comparison between the stationary and overstability cases when both boundaries are rigid.
![]()
Figure 7. A comparison between free and rigid boundaries for the stationary convection case.
![]()
Figure 8. A comparison between free and rigid boundaries for the overstability case.
rotation has a profound effect on the permeability of porous medium for the stationary convection case. In general the effect of permeability of porous medium is to destabilize the system. In case of no porosity it appears that the system is less stable than the corresponding one in presence of porosity.
Acknowledgements
The authors would like to thank Institute of Scientific Research and Revival of Islamic Heritage at Umm Al-Qura University (Project ID 43205018) for the financial support.
NOTES
![]()
*Corresponding author.