Received 23 January 2015; accepted 27 December 2015; published 30 December 2015
1. Introduction
The nonlinear partial differential equations of mathematical physics are major subjects in physical science [1] . Exact solutions for these equations play an important role in many phenomena in physics such as fluid mechanics, hydrodynamics, Optics, Plasma physics and so on. Recently many new approaches for finding these solutions have been proposed, for example, tanh-sech method [2] -[4] , extended tanh-method [5] , extended jacobain method [6] , modified simple equation method [7] [8] , sine-cosine method [9] [10] , homogeneous balance method [11] [12] , F-expansion method [13] -[15] , exp-function method [16] [17] , trigonometric function series method [18] ,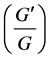 
-expansion method [19] -[22] , Jacobi elliptic function method [23] -[26] , the
-expansion method [27] -[29] and so on.
The objective of this article is to investigate more applications than obtained in [27] -[29] to justify and
demonstrate the advantages of the 
method. Here, we apply this method to (2+1)-dimensional
soliton breaking equation [30] and (3+1)-dimensional Kadomstev-Petviash-vili.
2. Description of Method
Consider the following nonlinear evolution equation
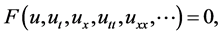(1)
where F is a polynomial in 
and its partial derivatives in which the highest order derivatives and nonlinear terms are involved. In the following,we give the main steps of this method
Step 1. We use the wave transformation
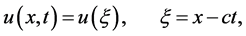(2)
where c is a positive constant, to reduce Equation (1) to the following ODE:
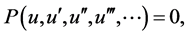(3)
where P is a polynomial in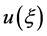 
and its total derivatives,while
.
Step 2. Suppose that the solution of ODE (3) can be expressed by a polynomial in 
as follows
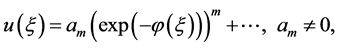(4)
where ![]()
satisfies the ODE in the form
![]()
(5)
the solutions of ODE (5) are
when ![]()
![]()
(6)
when ![]()
![]()
(7)
when ![]()
![]()
(8)
when ![]()
![]()
(9)
when ![]()
![]()
(10)
where ![]()
are constants to be determined later,
Step 3. Substitute Equation (4) along Equation (5) into Equation (3) and collecting all the terms of the same power![]()
, ![]()
and equating them to zero, we obtain a system of algebraic equations, which can be solved by Maple or Mathematica to get the values of![]()
.
Step 4. substituting these values and the solutions of Equation (5) into Equation (3) we obtain the exact solutions of Equation (1).
3. Application
Here, we will apply the ![]()
method described in Section 2 to find the exact traveling wave solutions and then the solitary wave slutions for the following nonlinear systems of evolution evolution equations.
3.1. Example 1: The (2+1)-Dimensional Breaking Soliton Equations
Let us consider the (2+1)-dimensional breaking soliton equations [30] :
![]()
(11)
where ![]()
is known constant. Equation (11) describes the (2+1)-dimensional interaction of a Riemann wave propagating along the y-axis with along wave along the x-axis. In the past years, many authors have studied Equation (11). For instance, Zhang has successfully extended the generalized auxiliary equation method of the (2+1)-dimensional breaking soliton equations in [31] . Some soliton-like solutions were obtained by the generalized expansion of Riccati equation in [32] . Recently, a class of periodic wave solutions were obtained by the mapping method in [33] . Two classes of new exact solutions were obtained by the singular manifold method in [34] .
Using the wave variable ![]()
and proceeding as before we find
![]()
(12)
Integrating the second equation in the system and neglecting constant of integration we find
![]()
(13)
Substituting (13) into the first equation of the system and integration we find
![]()
(14)
Balancing ![]()
and ![]()
in Equation (14) yields,![]()
. Consequently, we get the formal solution
![]()
(15)
where![]()
, ![]()
, ![]()
are constants to be determined, such that![]()
. It is easy to see that
![]()
(16)
![]()
(17)
Substituting (15) and (17) into Equation (14) and equating all the coefficients of![]()
, ![]()
, ![]()
, ![]()
, ![]()
to zero, we deduce respectively
![]()
(18)
![]()
(19)
![]()
(20)
![]()
(21)
![]()
(22)
From Equations (18)-(22), we have the following results:
Case 1.
![]()
Case 2.
![]()
So that the exact solution of Equation (14)
Case 1.
when ![]()
![]()
(23)
when ![]()
![]()
(24)
when ![]()
![]()
(25)
when ![]()
![]()
(26)
when ![]()
![]()
(27)
Case 2.
when ![]()
![]()
(28)
when ![]()
![]()
(29)
when ![]()
![]()
(30)
when ![]()
![]()
(31)
when ![]()
![]()
(32)
3.2. Example 2: The (3+1)-Dimensional KP Equation
We next consider the (3+1)-dimensional KP equation
![]()
(33)
Xie et al. [35] obtained non-traveling wave solutions by the improved tanh function method, in which they introduced a generalized Riccati equation and gained its 27 new solutions. In this paper, we will construct new non-traveling wave solution of Equation (33). As a result, new non-traveling wave solutions including soliton- like solutions and periodic solutions of Equation (1) are obtained. A generalized variable-coefficient algebraic method with computerized symbolic computation is developed to deal with (3+1)-dimensional KP equation with variable coefficients in [36] . Chen et al. [37] study (3+1)-dimensional KP equation by using the new generalized transformation in homogeneous balance method.
Using the wave variable![]()
, the Equation (33) is carried to an ODE of the form
![]()
(34)
Integrating twice and setting the constants of integration to zero, we obtain
![]()
(35)
Balancing ![]()
and ![]()
in Equation (35) yields,![]()
. Consequently, we get the formal solution (15).
Substituting (15)-(17) into Equation (35) and equating the coefficients of![]()
, ![]()
, ![]()
, ![]()
, ![]()
to zero, we respectively obtain
![]()
(36)
![]()
(37)
![]()
(38)
![]()
(39)
![]()
(40)
From Equations (36)-(40), we have the following results:
Case 1.
![]()
Case 2.
![]()
So that the exact solution of equation
Case 1.
when ![]()
![]()
(41)
when ![]()
![]()
(42)
when ![]()
![]()
(43)
when ![]()
![]()
(44)
when ![]()
![]()
(45)
Case 2.
when ![]()
![]()
(46)
when ![]()
![]()
(47)
when ![]()
![]()
(48)
when ![]()
![]()
(49)
when ![]()
![]()
(50)
4. Conclusion
The ![]()
method has been successfully used to find the exact traveling wave solutions of nonlinear evolution equations. As an application, the traveling wave solutions for (2+1)-dimensional soliton breaking equation and (3+1)-dimensional Kadomstev-Petviash-vili which have been constructed using the modified simple equation method. Let us compare between our results obtained in the present article with the well-known results obtained by other authors using different methods as follows: Our results of (2+1)-dimensional soliton breaking equation and (3+1)-dimensional Kadomstev-Petviash-viliare are new and different from those obtained in [38] [39] . Figures 1-4 show the solitary wave solutions of equations. It can be concluded that this method is
![]()
Figure 1. Solution of Equations (23)-(25).
![]()
Figure 2. Solution of Equations (26) and (27).
![]()
Figure 3. Solution of Equation (41)-(43).
![]()
Figure 4. Solution of Equation (44) and (45).
reliable and propose a variety of exact solutions NPDEs. The performance of this method is effective and can be applied to many other nonlinear evolution equations.